小数据条件下基于测地流核函数的域自适应故障诊断方法研究
2018-09-28刘海宁宋方臻窦仁杰黄亦翔刘成良
刘海宁, 宋方臻,窦仁杰, 黄亦翔, 刘成良
(1. 济南大学 机械工程学院,济南 250022; 2.上海交通大学 机械与动力工程学院,上海 200240 )
设备状态监测与故障诊断在维护生产秩序,杜绝生产事故、保证产品质量等诸多方面发挥着日益明显的作用,被认为是实现工业4.0的基础[1]。智能故障诊断能够模拟人类思维的推理过程,通过有效地获取、传递和处理诊断信息,模拟人类专家,以灵活的诊断策略对监测对象的运行状态和故障做出智能判断和决策[2],因此基于人工智能的故障诊断方法被学术与工业界广泛研究。但是,智能故障诊断方法投入工程实际应用不可回避的一个障碍是:智能故障诊断方法[3]必须通过对大量先验样本数据的机器学习才能建立其一定的故障诊断能力。对机械设备故障诊断来说,为获取有价值的先验样本数据,需要在采样母体、工况、故障类型上实现最大化,否则无法建立对设备状态变化规律及表现的一般性认知。但实际工程应用中受人力、物力及时间等客观条件限制,先验样本数据的采样空间被极大地压缩,智能故障诊断模型的精确性也就无法保证。并且研究证明:在实验室用模拟故障所得到的特征信息的模式样本在模式空间中的类聚性,与实际生产中所得到的模式样本的类聚性有着很大差别,因为从统计角度讲他们不属于同一个母体[4]。具体到广泛采用的基于振动信号的设备故障来说,由于工况条件不同,以及材料成分、制造工艺、装配误差等因素造成的个体差异都会影响机械零部件的振动特性。从模式识别角度来讲,先验样本数据质量欠佳使得基于先验样本数据训练的故障诊断模型的泛化能力[5]无法满足实际设备状态监测的需要。
先验样本数据少,样本空间不完备是机械设备故障诊断必须面对的“小数据”困境。但是对于不同数据稀缺问题的解决方式是不同的:故障类型的受限问题可以通过智能诊断模型的进化或在线学习的方式来解决,如Yin等[6]基于增量支持向量数据描述与极限学习机构造了一个具有进化学习能力的故障诊断模型,在连续的设备状态监测中不断更新其诊断模型的诊断能力。但是对于采样母体和工况条件受限的问题,则需要寻求其他的理论依据。刘刚等[7]采用Bootstrap方法对估计子的置信区间进行估计,在小数据情况下采用指标的稳定行为量来确定故障特征指标。受此启发,瞿雷等[8]采用稳定性与敏感性联合评估方法对特征进行评估,并利用核主成分分析方法提取剩余联合特征中的非线性特征,实现不同齿轮故障状态的分类。Sun等[9]结合Bootstrap与遗传算法研究了最优复合特征搜索方法,并将其应用在发动机的故障诊断。Cerrada等[10]利用随机森林(Random forest)方法对小数据、多特性数据分类的鲁棒特性,结合遗传算法对振动信号高维特征进行选择以实现对齿轮的故障诊断建模。
上述方法共同点在于通过寻找特征分布中的数值稳定性指标来解决诊断模型泛化能力变差的问题。但是在实际的设备状态监测过程中,特征分布的数值稳定性指标不易寻找,特别是当面对机械设备工况变化、母体差异时,基于小数据数据获取的数值稳定性指标难以应对更为复杂的设备状态识别需要。本文结合测地流核函数(Geodesic Flow Kernel, GFK)[11]方法提出基于域自适应(Domain Adaptation)理论的故障诊断方法,旨在以特征分布结构上的相似性为判别依据进行设备状态的识别,从而抑制工况及监测个体差异两类因素导致的特征分布偏移,有效提高智能诊断模型在实际设备状态监测应用中的泛化能力。
1 域自适应学习理论
在域自适应的具体方法上,基于格拉斯曼流形的方法、基于深度学习的方法、基于低秩逼近的方法等[15]方法被提出并取得了较好的学习效果。其中,基于测地流核函数的方法旨在基于数据的内蕴结构性特征进行模式识别,能够克服由于数据在数值或空间分布上的不稳定性造成的泛化能力下降的问题,这就为解决设备故障诊断面临的“小数据”困境提供了有效的理论工具。同时,作为一种非监督的域自适应方法,兼具较好的计算效率,基于测地流核函数的方法对于设备状态监测具有较好的适应性。
2 基于测地流核函数的域自适应方法
理论研究与经验证据都表明,现实世界的数据中很自然地存在着某种子空间结构,而在机器学习中,特别是在统计建模中,输入数据也通常被嵌入一个低维线性子空间中,例如广泛采用的主成分分析(Principal Component Analysis, PCA)。Hamm[16]早在2008年提出了基于子空间的机器学习范式,将子空间结构上的相似性利用格拉斯曼流形上的距离函数进行度量。格拉斯曼流形G(d,D)是RD空间内一系列d维线性子空间的集合。在格拉斯曼流形上,子空间被映射为一点,子空间结构上的相似性就可以直观上通过映射点的距离测度进行评估。
而在域自适应问题中,源域数据与目标域数据由于数据偏移的问题,映射点可能距离较远,但是连接两个映射点构造测地流曲线就可以追踪子空间在几何与统计特性上的连续增量变化,如图1所示。Gopalan等[17]通过在测地流曲线上采样一定数量的中间子空间来匹配域迁移过程,并通过构造域无关特征以实现域自适应分类。Gong等进一步拓展了该方法,将原始特征在整个测地流上进行投影,而不只是在若干采样点上,并通过定义核函数实现距离测度的计算和分类器应用,具体来说:
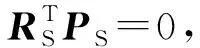
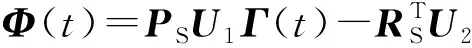
(1)
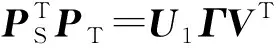
0≤θ1≤θ2≤…≤θd≤π/2
(2)
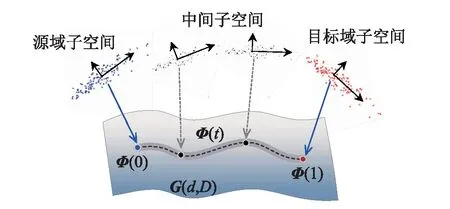
图1 格拉斯曼流形上基于测地流核函数的域自适应原理Fig.1 An overview of the domain adaptation methodology with GFK on Grassmann manifold
该角度是子空间重合度的一种测度。由此得到,Γ(t)与∑(t)分别是以cos(tθi)和sin(tθi)为元素的对角矩阵。
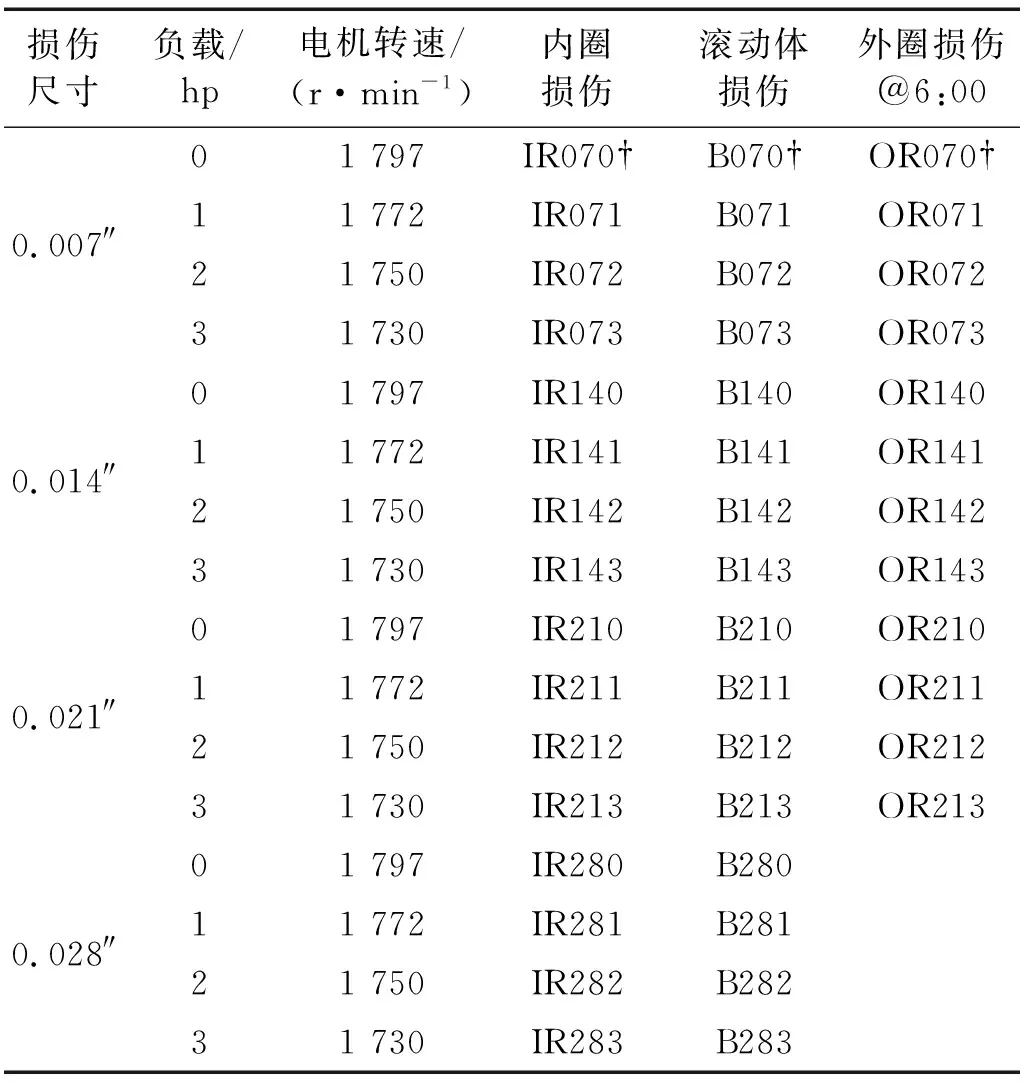
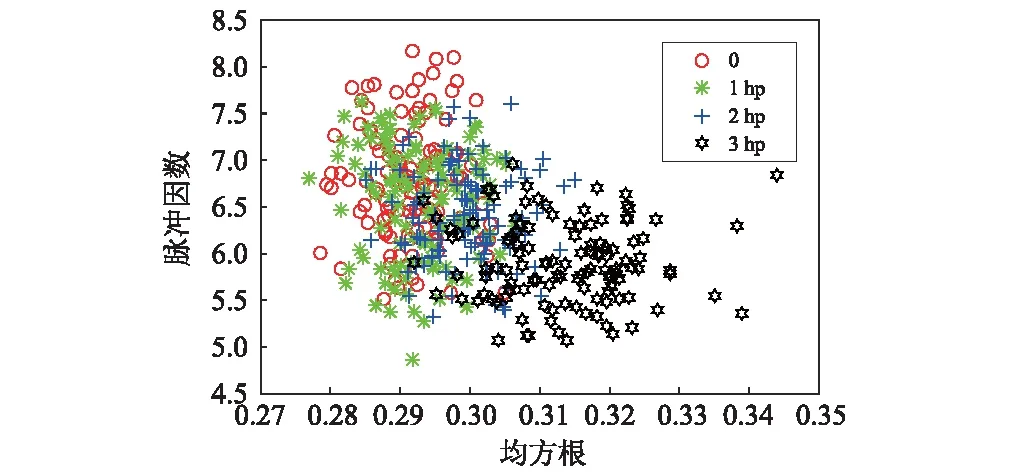
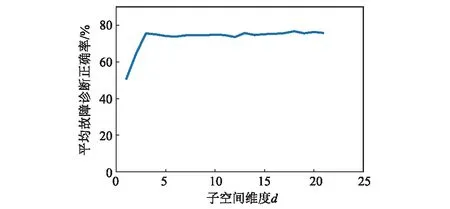
假设给定原始特征向量x,将其在测地流上投影,得到生成特征向量z∞=Φ(t)Tx。其中:当t=0时,z∞=PSx,即原始特征向量投影到源域数据子空间内;当t=1时,z∞=PTx,即原始特征向量投影到了目标域数据子空间内;而当0 (3) 式中:G∈RD×D是一个半正定矩阵,计算如下 (4) 式中:Λ1~Λ3为对角矩阵,对角元素为 (5) 基于上述定义,域无关特征向量z∞的距离测度可以方便地通过测地流核函数来进行计算 (6) 在此基础上即可应用分类器基于源域数据的机器学习实现对目标域数据的分类识别,而实际的分类则是在域无关特征空间内完成的。 针对机械设备故障诊断面临的“小数据”困境,结合基于测地流核函数的域自适应学习方法的特点,以机械设备状态监测广泛采用的振动数据为例,建立具备域自适应能力的设备故障诊断框架,如图2所示。 图2 基于测地流核函数的域自适应设备故障诊断框架Fig. 2 Domain adaptive machinery fault diagnostic framework based on GFK 根据域自适应学习设定,以有标签的历史振动数据为源域,以待识别振动数据为目标域,进行基于测地流核函数的域自适应方法应用。具体地,该框架的执行可分为3个主要步骤: 步骤1 设备状态子空间的构造。分别对源域和目标域振动数据进行特征提取、特征选择,并通过主成分分析进行设备状态子空间的构造。其中,特征选择的目的在于从所提取特征中选取敏感特征,此处所谓敏感特征根据基于测地流核函数方法的计算特点应当以设备状态子空间的构造为目的;主成分分析的目的在于获取子空间的线性结构。 步骤2 进行测地流核函数的计算。联合源域子空间与目标域子空间形成格拉斯曼流形,连接源域与目标域子空间在格拉斯曼流形上的映射点构造测地流,并分别将源域特征子空间与目标域特征子空间在测地流上投影,基于式(4)进行核函数的计算。 步骤3 应用测地流核函数进行故障诊断。基于式(6)应用测地流核函数进行目标域特征与源域特征距离测度的计算,然后应用分类器识别并输出目标域振动数据的设备状态。 需要指出的是,本文应用域自适应方法旨在解决同种同型零部件在采样母体和工况条件受限情况下先验样本空间不完备而导致的智能故障诊断模型泛化能力变差的问题,对于更加复杂的不同型号、不同种类零部件之间的智能诊断应在迁移学习[18]理论框架下进一步加以研究。 为便于相关研究进行比证,本文采用美国西储大学的开放轴承振动数据集[19]进行试验验证。试验装置示意,如图3所示。左侧是一个2 hp的三相感应电动机,右侧是用于产生额定负载的测力计,二者通过扭矩传感器对准配合,被测对象为安装在电机驱动端的深沟球轴承,振动传感器安装在电机的驱动端上侧。 图3 轴承试验装置示意图Fig.3 Schematic diagram of the bearing test stand from case western reserve university 试验验证所选择的振动数据包括正常轴承振动数据,如表1所示。模拟故障轴承振动数据,如表2所示。所施加工况变化是指分别为0, 1 hp,2 hp和3 hp的载荷变化以及对应的电机转速变化。其中所模拟的故障包括:内圈损伤、滚动体损伤以及在6点钟方向上的外圈损伤,故障损伤尺寸分别为0.007″,0.014″,0.021″和0.028″。所测试深沟球轴承型号均为6205,其中前3种损伤尺寸所用轴承为SKF公司生产,最后一种损伤尺寸所用轴承为NTN公司生产。所有振动数据采样频率均为12 kHz。 表1 正常轴承振动数据集 典型的智能诊断模型的验证对训练样本和测试样本往往采取同质化方案,即训练样本和测试样本包含相同的工况、母体和故障尺寸。而为了验证小数据条件下的域自适应故障诊断方法,建立试验验证方案如图4所示。 表2 轴承振动数据集 图4 小数据条件下域自适应故障诊断方案Fig. 4 Small data scenario setting for machinery fault diagnosis based with domain adaption 上述方案设定旨在以轴承这一典型旋转零部件构造小数据条件下的机械故障诊断。选取载荷为0、转速为1 797 r/min正常状态下的振动数据,以及故障尺寸为0.007″的故障振动数据作为先验振动数据(表1与表2中后缀为“†”的数据),即源域,表1与表2中所有其他数据为待诊断数据,即目标域。在此方案设定下,变化的工况包括负载1 hp, 2 hp, 3 hp及对应的转速变化,变化的采样母体包括0.014″,0.021″及0.028″不同损伤程度下的不同轴承个体。相较于单纯的轴承个体变化,诊断条件更为苛刻。从统计上来说,该方案设定是基于4种数据样本的小数据条件来诊断44种变工况和变采样母体的数据样本。 为了验证域自适应故障诊断的可行性及基于测地流核函数的域自适应故障诊断方法的有效性,在特征选择上,选取轴承智能故障诊断广泛采用的时域和小波域特征。其中,在时域提取振动信号时域上的10个特征参数:峰峰值、均值、标准差、均方根、波形因子、偏斜度、峭度、波峰因数、间隙因数、脉冲因数。在小波域,基于“db10”小波基函数将振动信号进行5层分解,并提取32个频带的小波能量特征。将表1与表2中所有振动信号进行1 024个采样点的定长分割,分别提取时域与小波域特征,构造42维的特征向量。 在小数据条件下,训练集或先验数据的统计分布必然有别于测试集或监测数据。为了直观展现特征分布的偏移情况,选取内圈损伤故障模式下振动信号时域内均方根和脉冲因数特征进行二维特征分布空间的绘制,如图5所示。其中,图5(a)为载荷变化时下特征分布偏移变化情况:随着载荷增大,振动信号的均方根值逐渐增大,而脉冲因数逐渐减小,但偏移量均较小;图5(b)为故障尺寸变化时特征分布偏移情况:不同损伤尺寸条件下特征分布偏移更为明显,且同一损伤尺寸下特征分布呈现较强类聚性。 (a)工况变化 (b)损伤尺寸变化图5 工况与损伤尺寸变化情况下的内圈损伤特征分布偏移Fig.5 The demonstration of feature distribution deviation of inner race fault bearings under varied working conditions and fault diameters 两种情况对于小数据条件下的故障诊断均提出了较大挑战。如果说图5(a)中的特征分布偏移问题一般可以通过特征选择、优化分类器参数等方法加以解决;那么图5(b)中特征分布对于同类故障类聚性的明显背离则显得更为棘手。同时需要指出的是,基于小数据的先验知识寻求整体的故障诊断准确率最大化应当是域自适应故障诊断所追求的目标。 在特征选择上,由于测地流核函数方法的基本思想是基于子空间机器学习基础上的结构相似性评估,因此特征选择以优化轴承状态子空间的构造为目的。在上述特征提取的基础上,本文采用改进的距离评估(Improved Distance Evaluation, IDE)[20]法对所提取特征进行选择。其中,IDE方法一个关键参数是距离阈值的选择。通过遗传算法的参数优化表明,距离阈值并非越大越好,因为阈值太大会压缩子空间维度的选择范围。参数优化后,选取距离阈值为0.1进行特征选择,构建轴承状态子空间。 在特征提取的基础上,基于图4中小数据条件域自适应故障诊断方案设定,应用测地流核函数方法进行4种轴承状态的诊断。其中,测地流核函数方法应用的一个关键参数是子空间维度d的选择。为了揭示该参数对诊断准确度的影响,以子空间维度d为变量进行故障诊断迭代计算,其中每次随机抽取一种轴承状态下50个样本,共200个样本,来诊断其他所有数据样本,共迭代20次来求平均诊断准确率,结果如图6所示。 图6 子空间维度d对基于测地流核函数的故障诊断的影响Fig. 6 The average diagnostic accuracy with GFK under different dimensions of subspace 从图6可知,在子空间维度d>3的情况下,基于测地流核函数的域自适应故障诊断准确率趋于稳定。在实际验证过程中,取d=18,此时平均故障诊断准确率为76.7%。其中,该方法对于不同工况和不同故障尺寸条件下轴承状态的识别正确率,分别如表3与表4所示。 从表3与表4可知,基于测地流核函数的域自适应故障诊断有以下特点:①基于测地流核函数的域自适应故障诊断能够正确区分健康轴承与损伤轴承;②在损伤尺寸为0.007″时,该方法基于负载为0的轴承振动数据能够有效识别负载变化为1 hp, 2 hp, 3 hp时的轴承状态,同时在其他损伤尺寸条件下,对负载变化后的轴承状态识别正确率基本稳定;③当损伤尺寸分别变化为0.014″,0.021″, 0.028″时,该方法能够识别大多数轴承状态,特别是对于损伤尺寸为0.028″时,识别正确率相对较高。需要注意的是,该损伤尺寸下的轴承为NTN公司的轴承,而其他损伤尺寸下的轴承为SKF公司的同型不同个体的轴承。由此可以看出,该方法能够在一定程度上克服母体差异造成的数据偏移对故障诊断的影响。 但是需要指出的是,从表4可知,该方法对于损伤尺寸为0.021″时的内圈损伤识别正确率很低。检视0.021″内圈损伤尺寸的小波能量特征分布,发现其与其他损伤尺寸轴承的特征分布差别较大,从而造成对其状态识别准确率下降。这也说明在特征提取上存在进一步研究和优化的空间。 表3 基于测地流核函数的域自适应故障诊断方法 表4 基于测地流核函数的域自适应故障诊断 基于子空间的机器学习是基于测地流核函数的域自适应故障诊断的理论基础。与之对应的一个典型方法是支持向量机(Support Vector Machine, SVM)。基于SVM的故障诊断是在特征提取的基础上通过构建分类超平面来对设备状态子空间进行划分。虽然SVM能够实现线性或非线性的分类,但SVM对于分类超平面的学习是基于已知的源域有标签数据,而对于待识别的目标域数据与源域数据之间的数据偏移并未进行建模考虑。 为了对比故障诊断效果,本文基于图4验证方案,在特征提取和基于IDE方法的特征选择基础上,采用libSVM软件[21]进行轴承状态识别,在进行参数优化后的识别结果表明:SVM能够对正常轴承状态实现100%的有效识别,对3种故障轴承状态的平均识别正确率为56.3%,具体结果如表5所示。 表5 支持向量机对3种故障轴承状态的识别正确率 对比表5与表4的验证结果可知:①在平均识别正确率上,基于支持向量机的故障诊断要小于基于测地流核函数的域自适应故障诊断;②对于损伤尺寸为0.014″的外圈故障状态以及损伤尺寸为0.028″的滚动体故障状态,SVM方法的故障诊断识别正确率降为0;③在多个损伤尺寸中,随着负载变化,SVM方法的故障诊断识别正确率变化较为明显。 综合来看,上述SVM方法故障诊断识别正确率的下降的原因在于基于损伤尺寸为0.007″条件下构造的轴承状态分类超平面无法适用于数据偏移后的轴承状态子空间。而数据偏移的原因在验证方案设定中是负载导致的工况变化,以及损伤尺寸变化及潜在的数据采样母体的变化,典型的数据偏移如图5所示。通过以上对比可见,基于测地流核函数的域自适应故障诊断方法在抑制工况变化和母体差异的影响,提高故障诊断正确率上作用较为明显。 本文从设备状态监测与故障诊断的实际需要出发,基于测地流核函数方法提出了小数据条件下的域自适应故障诊断框架,通过将源域与目标域特征嵌入格拉斯曼流形来寻求特征分布结构上的相似性进行故障诊断。基于轴承振动数据的试验验证表明,基于测地流核函数的域自适应故障诊断能够有效抑制工况、母体差异对设备状态识别的影响。同时,作为一种非监督的域自适应方法,基于测地流核函数的域自适应故障诊断更适合设备状态监测应用。另外,在域自适应故障诊断的理论框架下,仍有以下问题需要进一步深入研究: (1) 在特征提取上,需要从特征分布结构稳定性的角度进行有效的特征提取和特征选择方法研究,从而为测地流核函数的应用提供较好的数值基础。 (2) 在故障分类方法上,可以进一步结合测地流核函数进行非线性分类器应用或非线性子空间的探索,更好地提高域自适应故障诊断准确率。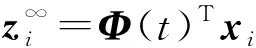
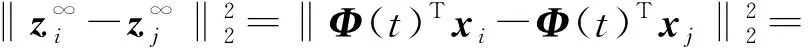
3 基于测地流核函数的域自适应故障诊断

4 试验验证
4.1 轴承振动数据


4.2 验证方案

4.3 特征提取与选择

4.4 基于测地流核函数的域自适应故障诊断结果


4.5 对比基于支持向量机的故障诊断方法

5 结 论
