圆周运动中的“最高点”与“最低点”问题

何兆训

中图分类号：G633.7 文献标识码：B 文章编号：1672-1578（2018）27-0171-01

除重力不计的带电粒子在匀强磁场中的运动，竖直平面内的圆周运动一般都是变速圆周运动，运动的速度大小和方向在不断发生变化，运动过程复杂，合外力不仅要改变运动方向，还要改变速度大小，所以一般不研究任意位置的情况，只研究特殊的临界位置──最高点和最低点。变速圆周运动的问题一直是较为难以理解，特别是物体处于重力场和电场等复合场中在竖直平面内做圆周運动的问题更是高中物理的重点和难点内容，在物理教学中很受老师关注，在各类考试中也倍受命题老师的青睐，学生答题的出错率非常高。分析学生出错的原因不难发现，不能准确分析圆周的“最高点”和“最低点”以及物体在“最高点”和“最低点”处具有怎样的特点与规律，是学生答题的最大障碍和瓶颈。那么有没有一种较为容易理解的方法来解决这个困扰学生的难题呢？

高中物理教学和学习中所牵涉到复合场主要是重力场，电场和磁场的复合。而又以重力场和匀强电场的复合，重力场和匀强磁场的复合，重力场，匀强电场和匀强磁场的复合等为主要表现。不管是哪种复合，找出圆周运动的“最高点”和“最低点”的解决问题的关键。这里提到的“最高点”和“最低点”并不是空间位置中的最高点和最低点，在只有重力场的情况下我们知道竖直平面内的圆周运动的最高点就是最高的那一点，最低点也就是最低那一点。因为在重力场的情况下速度最小的位置在最高的那一点，这一点向心力最小，速度最大的位置在最低的那一点，这一点向心力最大。所以我们通常用“最高点”和“最低点”来代表速度最小和速度最大的两个位置。那在复合场中我们又如何找出圆周运动速度最小的“最高点”和速度最大的“最低点”呢？这里我们可以从功能关系来得出答案。物体从“最高点”向“最低点”运动速度不断增大，合外力与速度夹角小于900做正功，物体“最低点” 向“最高点”运动运动速度不断减小，合外力与速度夹角大于900做负功。所以“最高点”和“最低点”应该是合外力与速度垂直的两个位置，也就是速度最小和速度最大的两个位置。其中重力与电场力的合力方向指向圆心的位置为“最高点”，那重力与电场力的合力方向背向圆心的位置也就是“最低点”。

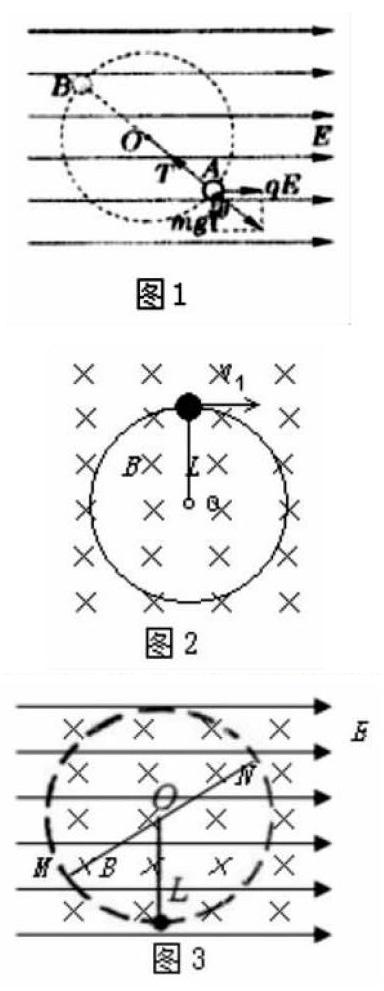
例1：如图1所示，在竖直平面内有一方向水平向右的场强为E=mg/q的匀强电场，一质量m，带电量为+q的小球，用长L细绳拴住悬于电场中O点，当小球处于平衡时，问在平衡位置以多大的速度释放小球，则能使之在电场中做竖直平面内的圆周运动？

分析：首先找出这个圆周运动的“最高点”和“最低点”，受力分析如图，通过计算可知重力与电场力的合力为2mg，方向与竖直方向成θ=450角斜向右下方。所以如图中的B点即为“最高点”，A点为“最低点”。而题目中出现的小球平衡时的位置就是指A点。 设小球在A点以速度V0释放时刚好可以到达最高点B，则它在B点细绳刚好没有拉力，有2mg=mV2B/L ①，从B到A运用动能定理有2mg×2L=mV20/2-mV2B/2 ②，由①②可得V0=（5gL）1/2

例2：如图2所示，垂直纸面向里的场强为B的匀强磁场中，一质量m，带电量为-q的小球，用长L细绳拴住绕电场中O点在竖直平面内做圆周运动，在最高点的速度为V1，问：V1为多少时小球可以做圆周运动？

分析：通过分析可知，圆周上的最高点就是小球在整个圆周运动中的速度最小的位置。由无支撑物的物体在竖直平面内做圆周运动的规律，在此位置速度最小的时候应该是细绳拉力刚好为0的时候。由mg+qVB= mV20/L，即可解得V0。当V1大于等于V0就可以保证小球在竖直平面内做圆周运动。这里值得注意的是，最高点的最小速度V0并不是等于（gL）1/2。

例3：如图3所示，在竖直平面内有一方向水平向右的场强为E=mg/q的匀强电场和垂直纸面向里的场强为B的匀强磁场中，一质量m，带电量为-q的小球，用长L细绳拴住绕电场中O点在竖直平面内做逆时针圆周运动，问小求在圆周运动过程中的什么位置速度最小，最小速度为多少？

分析：找出这个复合场中圆周运动的“最高点”和“最低点”，受力分析可知，重力与电场力的合力为2mg，方向与竖直方向成45°角斜向左下方。位置如图中的M点，在该处速度与和外力垂直，也是速度最大的位置即 “最低点” 。M点关于圆心对称的N点也就是速度最小的位置既“最高点”。由无支撑物的物体在竖直平面内做圆周运动的规律可知，在N点细绳拉力刚好为0时速度最小，设最小速度为V1，则由2mg-qV1B= mV21/L，便可解得V1的值。

变速圆周运动是高中物理力学中比较重要的一个知识，它同时又是圆周运动中最为复杂的一运动，因为它是速度和加速度都在时刻变化的一种变加速曲线运动。但不管多么难以理解的知识，都有克服和掌握它的方法。对于高中阶段出现的几乎所以的变速圆周运动问题，解决它们的基本思路和方法一般都有本质的联系，动能定理的灵活运用是理解变速圆周运动的基础，“最高点”和“最低点”的确定是突破变速圆周运动难点的关键，圆周运动规律的深刻把握是解决变速圆周运动的依据。