基于Gamma过程的交流接触器剩余电寿命仿真预测*

2018-09-27李奎李正广段宇郑淑梅刘政君高志成

电测与仪表 2018年16期

李奎，李正广，段宇，郑淑梅，刘政君，高志成

(1. 省部共建电工装备可靠性与智能化国家重点实验室，河北工业大学，天津 300130;2. 河北省电磁场与电器可靠性重点实验室，河北工业大学，天津 300130)

0 引言

交流接触器是一种频繁接通和分断电路的低压控制开关电器，在电力拖动和自动控制系统中应用最为普遍[1-2]。例如，在低压配电系统中的智能控制功能[3]，以及对电机正反转控制中，如冲床，都有很广泛的应用。交流接触器在一些重要的工业场合有大量应用，操作较为频繁。交流接触器每次开断会引起机械应力和电应力的损耗，随着损耗的持续累积，当达到失效阈值时接触器工作异常，可能会引起设备的意外停运甚至损坏。因此研究接触器的寿命状态对提高用电设备的安全运行水平有重要意义[4]。

可以通过预测产品的剩余寿命，来判断其寿命状态。目前，在开关电器剩余寿命预测方面国内外学者已经做了很多研究，也取得了很多的成果。近些年来，人工智能算法在设备状态评估方面取得了很大的突破[5-7]，文献[5]以继电器的超程时间和吸合时间为输入量，利用BP神经网络的方法建立继电器剩余寿命预测模型，对归一化处理后的试验数据进行训练，通过训练好的BP神经网络进行寿命预测，结果预测误差相对较小。该方法的特点是无需进行条件假设和建立统计模型，直接输入数据就可以预测出剩余寿命。另外，利用统计学的方法也可以对开关电器进行研究分析[8]。文献[8]首先得到HH52P型继电器的超程时间，将数据分区处理并融入超程时间回归模型中，将动作次数N作为回归变量，将预测变量Y作为因变量，建立两者的回归退化模型，得到超程时间的时序特征，实现继电器寿命预测。此外，在非开关电器方面有学者建立了基于Wiener过程的性能退化模型[9]，如文献[9], 以电子产品为例，利用自助法(Bootstrap)获取先验数据并确定退化模型参数的先验分布，由贝叶斯方法融合退化数据确定后验估计，最后由剩余寿命分布确定该电子产品的剩余寿命。该方法适用于非单调性能退化的过程，对单调变化的退化量可以用Gamma过程来描述。利用人工智能算法进行寿命预测的关键在于样本输入量的选择和预测模型的建立，且其性能好坏会受样本数据的数量和质量的影响，需要较多的试验数据进行训练；基于概率统计的预测方法的重点是根据随机过程建立数据模型，与人工智能的预测方法相比较，基于概率统计还可以得到预测结果的概率密度函数以及可靠度，更容易理解其求解的过程。

产品发生失效与其性能参数逼近极限状态有关，而产品性能参数逼近极限状态，通常是一个演变过程，可用随机过程建模的方式对其寿命进行预测[10]。Gamma过程模型是较为常用的随机过程建模方法，该过程模型是建立在Gamma分布的基础上，适用于描述连续腐蚀、磨损、疲劳等形式退化量渐变的过程。从交流接触器的失效机理来看，交流接触器每次开断产生的电弧会对触头系统造成一定的磨损，当触头系统磨损量累积达到失效阈值时会发生退化失效。触头系统的磨损量和燃弧的能量密切相关，因此可以利用燃弧侵蚀量作为交流接触器性能退化参数[11]，来反映触头系统磨损的累积。交流接触器每次的燃弧侵蚀量是独立同分布，可以通过中心极限定理使其累积燃弧侵蚀近似服从正态分布。在概率统计学中的多种分布模型很多是相互联系，甚至可以相互转化的。Gamma分布曲线较为灵活，其参数α、β数值的不同可以包括指数分布、正态分布以及其它曲线等，在医药、天文、航海等多种领域有十分广泛的应用[12-13]。Gamma过程模型在性能退化的可靠性建模中已得到了非常广泛的研究和应用。Yuan将Gamma过程应用于核电站元件的退化过程建模中[14]，为性能退化的核电站元件寿命的预测提供了更多的科学依据，并开发了一套用于校准模型参数的统计方法；Lawless和Crowder将协变量情形的Gamma过程应用到金属裂纹生长的建模当中[15]。

在基于概率统计的预测方法中，Gamma过程更适用于单调、非负增长的退化轨迹[13]，可以较好地反映退化过程中的不确定性，且可以给出退化系统的剩余寿命以及剩余寿命分布概率密度，在工程实际中有指导意义。文中通过直方图、皮尔逊卡方检验和经验分布函数图证明了可以利用Gamma过程模型对交流接触器建立退化模型。最后，利用该模型对其进行剩余寿命预测，并作出了误差分析。

1 基于Gamma过程的剩余寿命模型

1.1 Gamma分布

如果一元连续随机过程X(t)满足：

(1)X(0)=0；

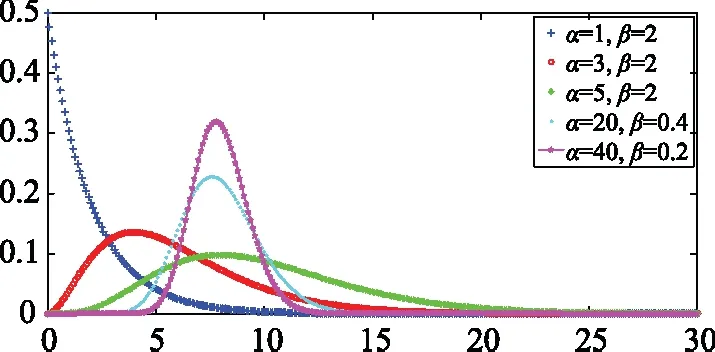
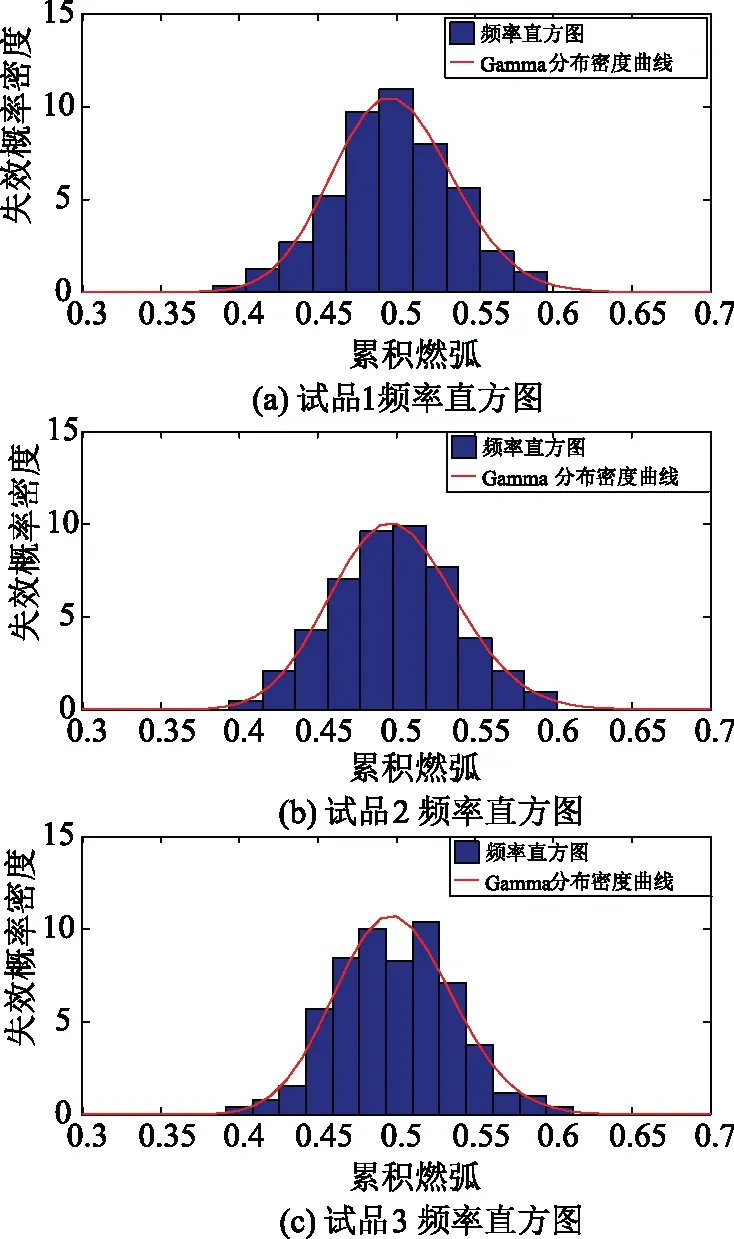
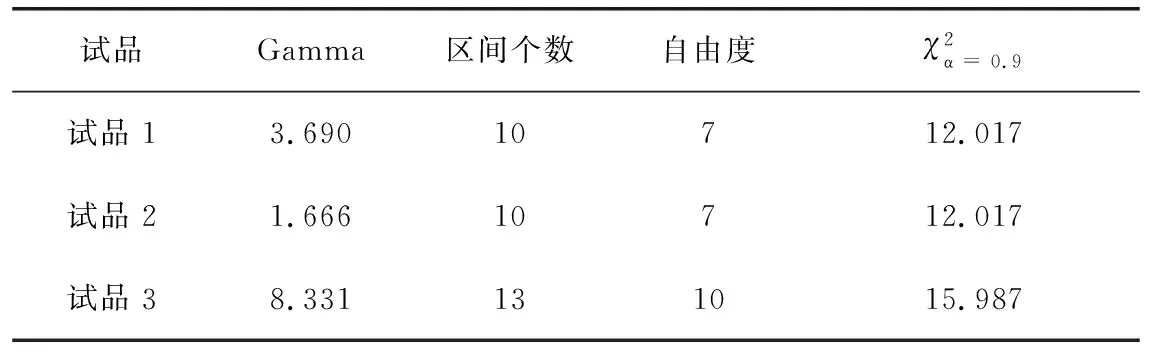
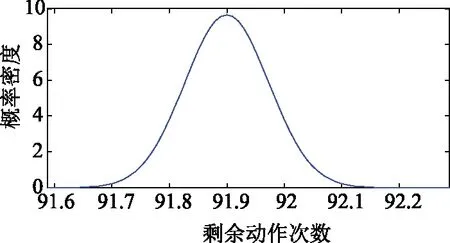
(2)X(t)有相互独立增量，即在任意时间区间[t1，t2]，[t3，t4]，且t1

(3)从t到t+Δt时刻，增量ΔX=X(t+Δt)-X(t)服从Gamma分布，即：ΔX～Gamma(α(t+Δt)-α(t),β)；

那么称{X(t),t≥0}这个随机过程服从Gamma(α(t),β)分布[16]，其中α(t)为其形状参数，β为其尺度参数。期望与方差分别为α(t)β，α(t)β2。

Gamma分布密度函数是：

(1)

将产品的失效阈值记为L，失效时间记为T，当退化过程到达预先设定的产品失效阈值L时，即：

T=inf{t|X(t)=L;t≥0}

(2)

失效时间T的分布函数：

(3)

失效概率密度函数为：

η(α(t))}zα(t)-1e-zdz

(4)

式中η(α)=Γ′(t)/Γ(t)=∂logΓ(α)/∂α,α>0。

1.2 参数估计

对模型当中的未知参量进行估计，α(t)是形状参数，描述预测变量对产品性能的影响，一般情况下取α(t)=kt，转换成了对k、β进行估计[17]。假设试验中有m个样品，对每个样品进行n次测试，Xij(i=1，2，…m，j=1，2，…n)表示第i个样品第j次测得的累积退化数据。特征参数退化量的增量Δxij=xi(j+1)-xij服从Gamma分布，用极大似然估计的方法对其中的参数进行估计，公式如下：

(5)

由公式(5)分别对k和β求偏导并等于零可以列出似然函数方程组，从而可以求出k、β的估计值。求出参数估计值之后，再通过公式(3)可以求出失效时间分布函数，但在实际应用中该方法求解出的失效时间分布函数比较复杂，不易处理。为了避免这个难题，可以利用B-S(Birnbaum-Saunders)分布的方法来逼近寿命T的分布[18]，并将L用L-L0代替，可得到剩余失效时间分布公式：

(6)

式中 Ф(·)是标准正态分布；c=(β/(L-L0))1/2；d=(L-L0)/kβ；L0为试品运行到T0时刻时燃弧累积侵蚀量。概率密度函数为：

(7)

进而得到服从Gamma分布的试品剩余寿命：

(8)

2 实例分析

2.1 交流接触器电性能退化模型

交流接触器电性能退化失效机理主要是由于触头系统达到了系统所能承受的电弧电流的侵蚀量而失效，大量文献表明侵蚀量与i2t成正比[19-20]，并且呈线性增加。在交流正弦电流下，不考虑其它因素对交流接触器寿命的影响，触头单次动作产生侵蚀量定义为：

(9)

式中ej为触头第j次分断产生的电弧侵蚀量；λ为电弧侵蚀常数，大小受到触头材料、结构及灭弧系统的影响；j=1,2,3…n为触头开断次数；ij表示第j次的分断电流。交流电弧电流的熄灭是在电流过零点，不考虑电弧重燃的现象，若φj为起弧相角，在相角π处灭弧，则求积分为：

(10)

2.2 交流接触器电寿命仿真预测

根据交流接触器动作的特点，可以对其每次的标幺值进行模拟仿真。利用Monte-Carlo方法可以对起弧相角为随机分断方式下的电寿命试验过程进行模拟仿真，仿真出三组数据，分别看做三个试品各自触头中首次达到失效阈值那一相的电弧侵蚀数据。

随机分断相角下仿真方法如下：

(1)在(0,π)上产生服从均匀分布的随机相角φj；

(2)通过公式(10)计算触头的电弧侵蚀量ej；

(3)计算触头的累积磨损量Ej，当Ej小于阈值L时，重复上述步骤；当Ej大于等于阈值L时，跳出程序，该结果即交流接触器的电寿命；

(4)将前3个步骤重复三次，可以得到三台试品的电寿命仿真数据，流程图如图1，表1为累积电弧侵蚀量仿真数据。

图2为不同参数下Gamma分布的形状曲线，由图可以看出当α与β的比值较大时Gamma分布密度曲线近似于正态分布。

用Gamma分布密度曲线与交流接触器累积电弧侵蚀量仿真数据频率直方图进行拟合，并通过皮尔逊卡方检验法和经验分布函数图来证明Gamma分布对交流接触器性能退化过程建模的实用性。根据交流接触器累积燃弧仿真数据可以做出频率直方图，并画出Gamma分布密度函数曲线，如图3所示。

图1 仿真过程流程图

表1 交流接触器累积电弧侵蚀量仿真数据

图2 Gamma分布图

图3 Gamma分布、正态分布频率直方图

在统计学中假设检验是统计推断中的一类重要问题，皮尔逊χ2拟合优度检验可以反映实际数据与原假设分布之间拟合的优劣程度，根据分组结果计算检验统计量，即：

(11)

表2 皮尔逊卡方检验结果

经验分布函数是根据样本得到的分布函数，通过计算累积分布函数，收敛到概率1，计算公式为式(12)。经验分布函数图是阶梯状图形，反映了样本观测数据分布情况，将接触器累积电弧侵蚀的经验分布函数图和Gamma分布函数曲线叠放在一起，可以看出Gamma分布与仿真数据的拟合程度。

(12)

式中x(1)，x(2)，…，x(l)，为累积侵蚀量从小到大的排序：x(1)≤x(2)≤…≤x(l)，如图4为三个试品经验分布函数和Gamma分布函数拟合图。

仿真数据的经验分布曲线和Gamma分布函数曲线拟合程度很好，几乎完全重合，进一步说明可以用Gamma过程对交流接触器性能退化过程进行建模，并进行剩余寿命预测。预测方法如下：

利用单个试品的试验数据建立剩余寿命预测模型，以试品1为例。试品1的寿命为30 089次，三个试品失效阈值均为H=150，对试品进行实时寿命预测，并进行误差分析。根据极大似然函数方程组可以估算出Gamma分布参数α、β，再由公式(7)、公式(8)预测出剩余寿命如表3。表3为在相应的动作次数阶段进行的寿命预测。

图4 经验分布函数和Gamma分布函数图

表3 试品1预测参数及剩余寿命

当试品1运行到30 000次时，应用概率密度函数即公式(7)，预测出的剩余电寿命为92，如图5所示。此时，试品1的实际剩余寿命为89次，预测值与实际值只相差3次。

图5 试品1剩余寿命概率密度函数

对三个试品进行剩余寿命预测及相对误差计算，画出相对误差图，如图6所示，其中相对误差计算公式为：

由图6可以看出，相对误差曲线比较平稳，在接近其寿命终结时相对误差会有一个明显的上升趋势。这是因为当动作次数越接近其寿命终结时，分母上的实际剩余寿命急剧下降，此时相对误差会大大增加。由图可知，相对误差较为平稳且几乎都在10%以下，满足了工程的需求，接近交流接触器的实际寿命，提高了其剩余寿命的预测精度。