基于聚类融合技术的电力用户负荷模式提取方法*

李玉娇，黄青平，刘松，陈雨，刘鹏

(华北电力大学 电气与电子工程学院，北京 102206)

0 引 言

随着智能电网的不断深入和推进，许多电力计量装置被装入电力网络，获得电网用户的实时数据，从而监测、控制和预测电能使用[1]，为电网安全、可靠、经济地运行打下基础。近年来，电网数据呈现出规模大、种类多、价值密度低等大数据特征。在智能电网大数据环境下对数据挖掘算法进行研究，准确、高效地提取出电力用户的负荷模式，充分挖掘出用户的用电行为习惯、电量消费规律等有用信息，为电力需求响应系统设计[2]、用电异常(计量、窃电等)检测[3]、电价目录改善[4]、负荷控制[5]、负荷预测[6]等提供强有力的支撑。正确且清晰的负荷模式可改善电力系统运行的可靠性、帮助用户节能改造、提高经济效益[7]。因此，研究如何有效提取电力用户的负荷模式具有重要的意义。

用电负荷模式提取技术主要是依据用户用电负荷曲线，通过各种统计机器学习方法，提炼出某一用户的用电特征或若干用户的典型用电特征。目前，国内外已有很多学者和专家运用聚类分析方法研究用户用电负荷模式。文献[8]提出使用核主成分分析(Kernel Principal Component Analysis, KPCA)方法对负荷数据进行降维，采用Kernel K-means算法对用户负荷进行聚类处理。该方法虽然提高了负荷曲线聚类的准确性，但需要提前设定核函数参数，且易受聚类数和初始分类影响，没有良好的稳定性。文献[9]将遗传算法的搜索能力与模拟退火算法进行综合，对传统模糊C均值(fuzzy C-means，FCM)算法进行改进，对初始聚类中心敏感和全局搜索能力不足得到了改善，但多次迭代使得算法时间及复杂度明显增加。文献[10]指出，各聚类方法特点不同，应用于负荷模式提取或者其他方面时并不存在一种算法总是优于其他聚类算法。

针对上述研究中存在聚类结果稳定性差、计算复杂度高、单一聚类算法泛化能力不强等问题，将结合降维方法和聚类融合的技术应用到提取电力用户负荷模式中。本文首先使用用户负荷数据集的KMO(Kaiser-Meyer-Olkin)与显著性水平(Sig)分析负荷变量间的相关性，根据累计方差贡献率确定主成分个数将数据冗余信息去除，再将降维后的特征向量与原特征向量分别聚类并从聚类准确度及聚类效率两方面进行对比。然后在此基础上提出一种基于聚类融合技术的电力用户负荷模式提取方法，并通过聚类有效性指标Silhouette对模式提取结果进行评价，达到负荷模式提取更快、更准确的目的。

1 负荷数据预处理

1.1 数据清洗

用于用户负荷模式提取研究的数据来自于用电信息采集系统，该系统可能受计量表计故障、数据库故障等多种因素影响，存在缺失数据、错误数据、相似重复记录等脏数据，因此，需要对数据进行清洗，将数据集中不符合分析要求的数据剔除或修正，从而保证数据的一致性、正确性、完整性[11]。常见的电力用户负荷脏数据类型如表1所示。

表1 用电负荷脏数据类型

甄别用户负荷数据集中脏数据需对数据进行规范性检查。首先，删除数据集中用户负荷重复记录的数据；其次，分析数据集中负荷数据缺失情况，将缺失量达到当日采集点20%以上的用户视为严重缺失并将其剔除，将其余数据缺失用户采用多平滑修正方法补足缺失值；再次，判断数据极大极小值产生原因是用户用电行为所致还是负荷毛刺；最终，将不符合用电业务特性的异常数据采用多平滑修正方法替换错误值，其中平滑修正及极大极小值成因判断公式为：

(1)

式中pi, j表示用户i在时刻j的用电负荷值；m是向前采集的点数；n是向后采集的点数。

1.2 典型负荷曲线生成

由于用户的用电情况可能因某些突发事件的发生或天气因素导致用电负荷曲线发生变化，为了更准确的反应用户自身的用电行为，本文采用加权平均移动法生成用户的典型负荷曲线，其处理方法如公式(2)：

(2)

式中pi, j, k表示电力用户i前k天在时刻j的用电负荷；wi表示用户i前k天时负荷数据对应的权重且w1+w2+…+wk= 1。

1.3 数据标准化

为了避免数据集中数值差异较大或者变量量纲不同等因素的影响，需进行数据标准化处理。假设共有i个样本，各样本有j个变量指标，则数据集可以用i×j矩阵P表示为：

(3)

对P进行最大-最小值标准化处理生成标准矩阵X，即：

(4)

式中m=1，2，…，i；n=1，2，…，j； min{pi, j} 和max{pi, j}分别表示用户i负荷的最小值和最大值。

1.4 数据降维

文献[12]指出对于负荷曲线在维数较高的情况下可能会表现出不理想的等距性，该情况使得距离测度的意义减小，因此当数据集规模较大时，为了提升聚类效率和准确率，需要对数据集进行降维处理。常用降维方法有自组织映射、sammon映射、主成分分析等。采用主成分分析(principal component analysis，PCA)法，它是一种基于特征提取和数据压缩的统计分析方法，通过多个原变量的一系列线性组合形成少数不相关的综合变量，且这些综合变量在不相关的前提下尽可能多地反应原变量信息[13]。xm,n={xm,n，n= 1, 2,…,j}表示用户m的负荷曲线，主成分分析的主要目的是在保证用户原有信息的前提下尽量减小j、减小数据存储空间、减少算法的计算时间。主成分分析具体步骤如下：

(1)求经过标准化处理后所得矩阵X的相关矩阵R，并计算R的特征值λ1≥λ2≥…≥λj与特征向量μ1，μ2，…，μj，即：

(5)

(2)求R的方差贡献率ηk和累计方差贡献率η∑(p)，进而对主成分的个数p进行确定，公式为：

(6)

(7)

数据集的信息由数据变量的方差体现，通过累计方差贡献率衡量，贡献率越高，所含信息越多。一般认为前p个主成分累计方差贡献率η∑(p)达到75%～ 95%时便包括了j个原变量绝大部分信息，从而确定主成分的个数为p[14]。

2 聚类融合

目前，当使用各种聚类算法进行聚类分析时，常常遇到对同一数据集用不同聚类算法进行聚类时聚类结果不同且事先不知数据集的任何先验信息的情况，或者当增加或减少样本数量时聚类结果会发生明显变化，即单一聚类算法稳定性不高的情况。为了得到聚类结果更佳、更稳健的聚类模型，本文将聚类融合方法应用于负荷模式提取中。首先，用四种聚类分析算法进行聚类，得到相互独立且存在差异的聚类结果，然后构建共识矩阵，计算用户属于每一类的概率值，最终将各算法的聚类成员融合成一组聚类成员，得到优于单一算法且更加稳定的聚类分析模型。

2.1 聚类融合的概念

聚类融合的概念由A. Strehl和J. Ghosh于2002年提出，其定义是：将一个数据集的不同划分结果组合成一个统一的划分结果，而不使用对象原有的特征，且统一的划分结果最大程度上包含了所有输入聚类结果对数据集的聚类信息[15]。具体过程为：假设数据集X有n个数据对象，表示为X={x1，x2，…，xn}，对数据集X执行N次聚类算法得到N组聚类成员N={H1，H2，…，HN}，其中，Hi(i=1，2，…，N)为第i次聚类得到的聚类成员。然后设计融合函数W，对N组聚类成员进行融合，得到新的聚类结果N’，其过程如图1所示。

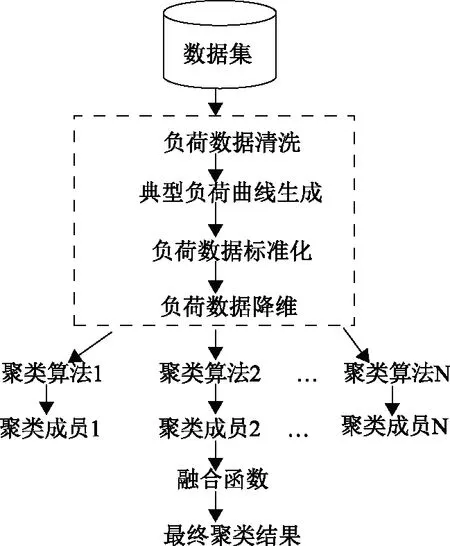
图1 聚类融合过程

2.2 聚类成员的生成

具有差异性聚类成员的生成通常有以下方法：

(1)使用同种聚类算法，初始参数设置不同，运行N次，目前常使用K-means算法;

(2)使用不同聚类算法，如K-means、Single-Linkage、Average-Linkage等产生多个不同的聚类结果。Fred等人[16]认为该方法可从不同角度挖掘数据集中有效信息;

(3)使用取样技术(例如：bagging、subsampling、bootstrap)获得数据集子集，然后对子集进行聚类。取样所得子集可代表整个数据集，可减少计算的时间以及降低计算的复杂性;

(4)使用一维投影或随机投影等技术将数据集的特征空间投影到数据子空间，得到数据集的多个子集，然后对子集进行聚类操作。

2.3 基于Co-association矩阵的融合函数

各聚类成员所构成的聚类簇结构如表2所示。其中，HN表示第N个算法的聚类成员，h1,h2,…,hn表示n个聚类簇，x1,x2,…,xm表示m个样本，数值“1”表示该样本属于该簇，数值“0”表示不属于该簇。

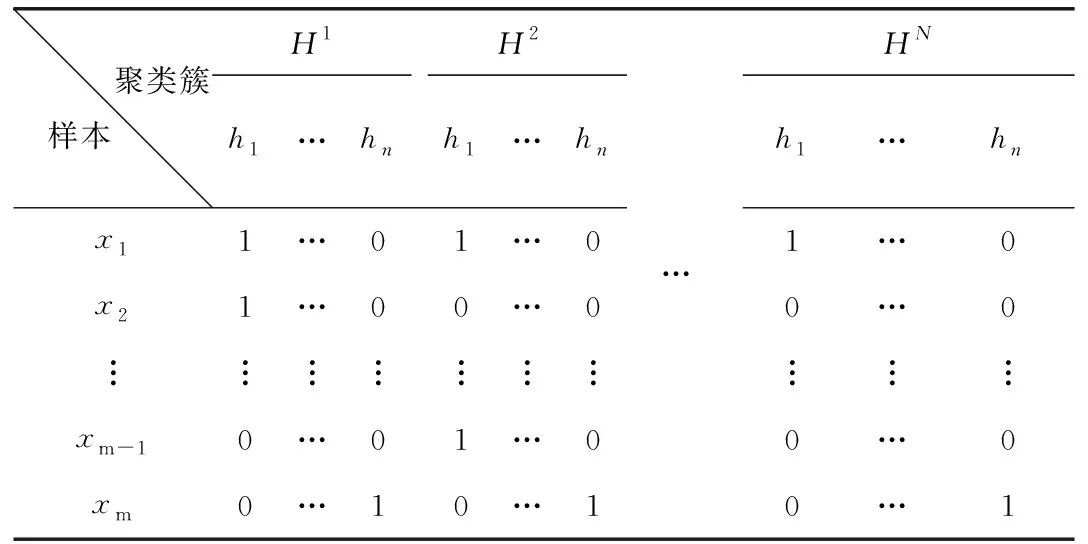
表 2 聚类簇分布结构

根据表2中所形成的0-1矩阵H构建Co-association矩阵S[17]，S中元素Sij表示样本i与样本j的相似度，其元素表达式为：

(8)

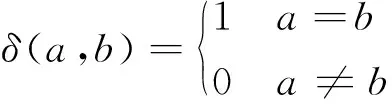
(9)

本文采用文献[17]所提出的阈值θ划分Co-association矩阵的方法进行聚类融合，θ取0.5。将矩阵S中元素Sij大于θ的设置为1，其余元素设置为0，所得到的0-1矩阵被视为新的Co-association矩阵，矩阵中同列为1的元素即认为属于同一类。

3 负荷模式提取

实验所用数据来源于某电网2014年1月份200个用户的日用电数据，采集间隔为15min，共计96个量测点。经过数据清洗后及数据预处理后，算例共包含184条有效日负荷曲线。算例在平台CPU为2.0 GHz、内存为2 GB的个人计算机上完成，实验数据经过MATLAB 2014a处理。

3.1 主成分提取

首先，对负荷数据集进行主成分提取可行性分析，由表3可知，KMO(Kaiser-Meyer-Olkin)值为0.904 > 0.7，sig值小于0.05，可知用户负荷数据间相关性较强，较适合进行因子分析。然后，分别计算相关矩阵R、R的特征值λ、特征向量μ、方差贡献率ηk及累计贡献率η∑(p)，并确定主成分个数p，部分计算结果如表4。

图2为特征值相对于成分个数的碎石图，可见前面部分曲线较陡峭，特征值大，所含信息多，后面部分曲线较平坦，特征值小，所含信息少。由图可直观看出，成分1至10左右包含了大部分信息，以后逐渐进入平稳。

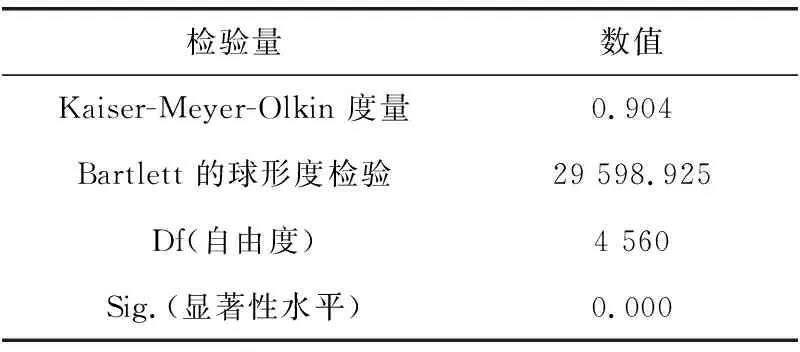
表3 KMO和Bartlett 的检验

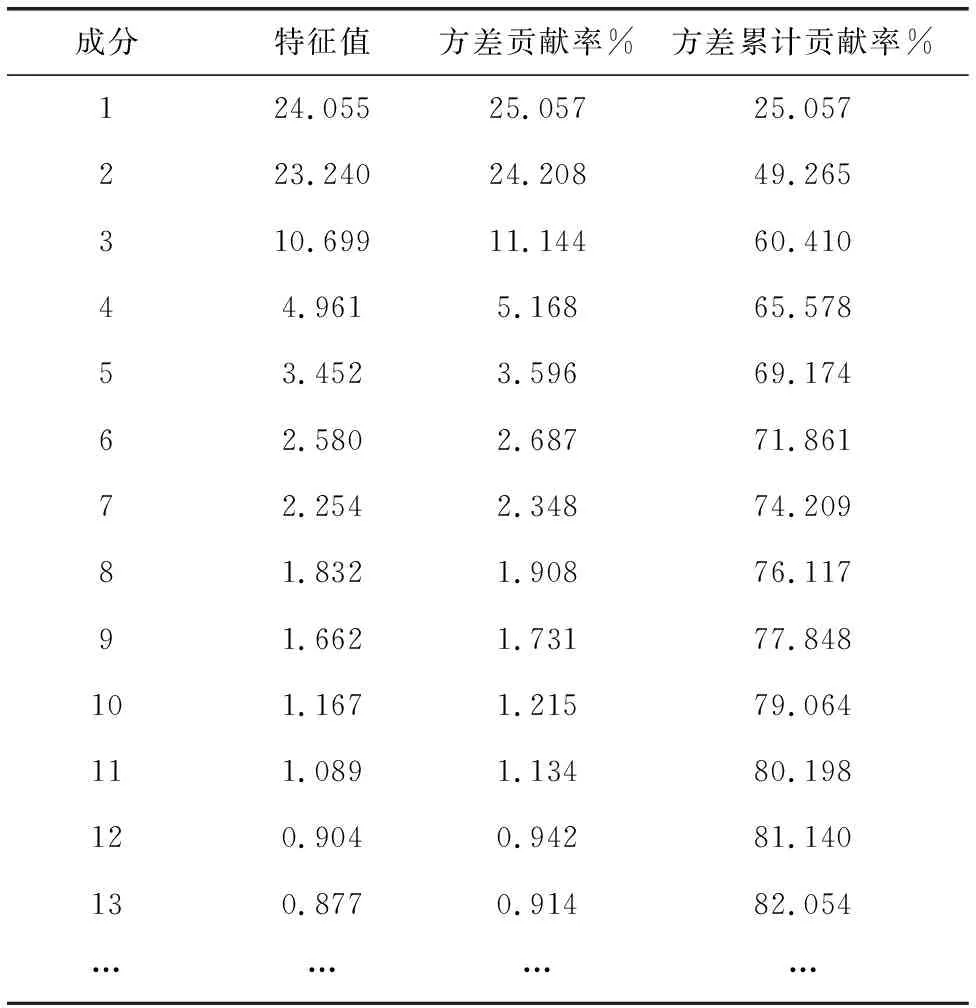
表4 方差及主成分贡献率

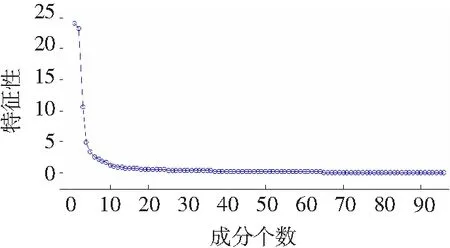
图2 碎石图

综合考虑图2趋势及表4累计贡献率，将主成分的个数确定为11。将184条负荷曲线分别用四种聚类算法(K-means、FCM、Single-linkage、SOM)进行聚类，降维前与降维后聚类时间(s)、聚类准确率(%)比较如图3所示。聚类效率分别提高27.99%、34.37%、30.16%、34.32%，聚类准确度分别提高1.63%、降低1.63%、提高0.54%、提高0.54%。由此可见主成分分析方法在保证聚类准确率基本不变的情况下有效地减少了数据存储空间以及算法运行时间。面对大数据环境下电力数据的日益增长，通过降维方法可以减少电力负荷数据冗余信息，从而减少分析时所需计算数据量，减少程序运行时所需存储空间。

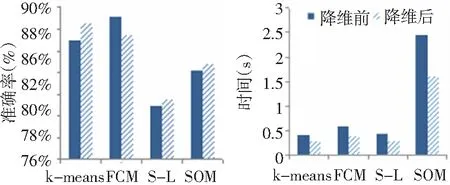
图3 降维前后聚类时间及准确度比较

3.2 聚类融合实验与分析

将原数据集矩阵与11项主成分所对应的特征向量矩阵相乘后作输入数据集，用上述四种聚类方法分别聚类，并基于Co-association矩阵进行聚类融合，将电力用户的负荷曲线聚为四类，聚类结果如图4所示，此时各类别的负荷模式有较为明显的用电特征，分别为双峰型用电模式、三峰型用电模式、平稳型用电模式、避峰型用电模式，其中红色曲线表示该类用户的典型用电规律。

图4 聚类结果

用聚类有效性指标Silhouette[18]对得到的负荷模式结果进行评估，该有效性指标可以反应类间分离程度和类内紧密程度，样本i的Silhouette指标值ISil(i)定义如下：

(10)

式中i表示数据集P中被划分为第j类的第i个用户数据；da(i)表示i与类内其余用户数据的平均距离，该值越小，表征类内紧密性越强；db(i)表示i与非类内其余用户数据的最小平均距离，该值越大，类间分散性越强。用户i的Silhouette指标值ISil(i) 取值范围为[-1，1]，db(i) 越大，da(i) 越小，ISil(i) 值越接近1，第j类的类内紧密性和类间分离性越强，聚类质量越好。若db(i)

表5 不同算法的Iave值比较

4 结束语

提出了一种基于主成分分析方法和聚类融合技术相结合的电力用户负荷模式提取方法，对于海量高维的电力用户负荷数据，首先采用主成分分析对数据集进行降维操作，然后使用聚类融合方法对降维所得综合变量作为新的数据集进行聚类操作，并用有效性指标Silhouette对聚类结果进行评估。算例表明该方法用于电力负荷模式提取可行，可提高模式提取的可靠性和有效性，可对电力大数据潜在的有用信息进行有效地挖掘，为负荷控制、负荷预测、电力策略制定等提供有力的支撑。