基于差值矩阵的多端输电线路故障定位研究*
2018-09-27高小刚谢李为曾祥君
高小刚,谢李为,曾祥君
(1. 国网冀北电力有限公司秦皇岛供电公司, 河北 秦皇岛 066000;2.长沙理工大学 电力与信息工程学院, 长沙 410114)
0 引 言
随着电力系统的规模不断扩大,高压输电线路的负荷量逐年增加,电力客户对电网安全运行的要求越来越高[1]。如何快速查找高压输电线路故障位置,实现故障的快速切除已经成为电力系统运行稳定性的重要保障[2]。
行波定位法作为故障定位最有效的方法之一被普遍使用。根据行波定位原理的不同,行波定位法分为单端行波法和双端行波法[3-5]。目前大多数高压输电线路的行波定位算法主要是针对双端输电线路,由于多端输电线路存在一个或多个T节点,使网络结构更加复杂,双端行波定位法基本上很难实现多端输电线路的故障精确定位[6]。
文献[7]通过定义初始故障行波到达三端输电线路时刻的隶属度进行支路判别,由于三端节点附近故障行波折反射复杂,容易造成判别困难。文献[8-10]提出了适用于三端输电线路的故障定位算法,但难以推广到多分支输电线路。文献[11]针对三端输电线路,通过相关性分析提取行波信号到达各端的时刻,但受反射波的干扰,难以实现多端输电线路的可靠定位。文献[12]通过结合双端和单端行波定位方法对多端输电线路故障分支进行判定和定位,但实际故障定位中反射波头识别困难,易造成较大定位误差。文献[13-14]针对多端输电线路,基于双端行波法,将支路判定和故障定位算法相结合求解故障位置,但计算过程繁琐。
针对多端输电线路故障定位的难点,提出一种基于线路故障分支判定矩阵的故障定位算法。首先计算故障前和故障后各线路距离矩阵的差值,得到故障分支判定矩阵,然后判别故障支路,利用故障分支判定矩阵中端点列元素计算故障点位置。
运用行波定位时,初始故障行波达到线路各端的时间影响着定位的准确性。文献[15]利用希尔伯特黄变换(Hilbert Huang Transform,HHT)检测故障行波信号,但其中的经验模态分解(Empirical Mode Decomposition,EMD)算法存在模态混叠现象和端点效应,造成测距误差较大。文献[16-17]采用 EEMD 和 ELMD 方法抑制EMD分解的模态混叠现象,但仍无法消除模态混叠和端点效应的影响。
为此,提出一种基于变模态分解算法(Variational Mode decomposition,VMD) 和Hilbert 变换相结合的故障行波波头检测方法,能够解决EMD 方法中存在的模态混叠现象和端点效应[18]。
通过ATP/EMPT仿真验证所提检测方法能更好地检测故障行波波头的到达时间,新的双端定位算法简单可行,定位误差小,能够进一步提高定位精度。
1 基于VMD与Hilbert变换的行波检测方法
变模态分解(VMD)是一种完全非递归的模态变分方法,利用多个维纳滤波组实现滤波,其模态分量和中心频率的表达式分别为[18-20]:
(1)
(2)
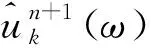
VMD算法实现流程如下:
(2)利用公式(1)和公式(2)分别更新uk和ωk,循环直至K次结束;
输电线路发生故障时,由于三相线路间存在耦合现象,线路故障电磁暂态过程中各行波相量相互干扰,通常采用凯伦布尔变换矩阵对互相耦合的系统进行相模变换,分解成0、1和2三个相互独立的模分量,其中1、2为线模分量,0为零模分量。
课题组提出从CVT接电线采用行波传感器提取行波信号[21]。利用行波传感器采集输电线路的电流行波信号,通过凯伦布尔变换对故障行波信号进行解耦变换,将解耦得到的分量信号进行VMD分解,利用Hilbert变换提取模态分量IMF1的瞬时频率,标定第一个瞬时频率的奇异点位置。
2 基于线路差值矩阵的多端输电线路定位方法2.1多端输电线路故障分支判定矩阵
图1为多端输电线路简图,线路共有K个T节点和n个端点。当线路发生故障时,故障行波将从故障点沿输电线路传输到各线路末端,在波阻抗不连续的点发生折射和反射。故障发生前,每条分支线路以首端点最近的T节点为分支基准,计算输电线路各分支长度的差值.如线路M1端支路和线路M2端支路、M3端支路的距离差值为:
ΔlM1M2=lM1T1-lM2T1
(3)
ΔlM1M3=lM1T1-lM3T1
(4)
式中lM1T1为线路M1T1的长度;lM2T1为线路 M2T1的长度;lM3T1为线路M3T1的长度。
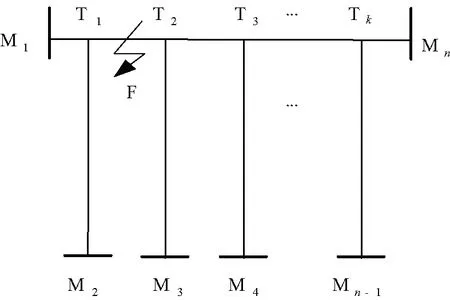
图1 多端输电线路简图
因此故障前各输电线路固有距离的差值矩阵如下:

其中,M3端的列元素为ΔlM3M1=lM3T2-lM1T2、ΔlM3M2=lM3T2-lM2T2、…、ΔlM3Mn=lM3T2-lMnT2。
故障发生后,假设以线路M2端为首端,以离线路M2端最近的T1节点为分支基准,计算输电线路各分支长度的差值。根据双端行波定位公式,可得线路M2M3中故障点到M2端和M3的距离分别为:
(5)
式中lM2M3是线路M2M3的长度;tM2、tM3分别是故障初始行波到达线路M2和M3两端的时间,v是故障初始行波的传输速度。
线路M2端支路距离与线路M1端支路、M3端支路的距离差值为:
ΔdM2M1=dM2-dM1=v(tM2-tM1)
(6)
ΔdM2M3=dM2-dM3=v(tM2-tM3)
(7)
式中v为故障行波的传输速度;tM1为故障初始行波到达M1端的时间;tM2为故障初始行波到达M2端的时间;tM3为故障初始行波到达M3端的时间。故障后各输电线路的距离差值矩阵为:

计算故障后各输电线路距离差值矩阵与故障前各输电线路固有距离差值矩阵的差值,得到故障分支判定矩阵,限于篇幅,只列出其中M3端的列元素为ΔdM3M1-ΔlM3M1、ΔdM3M2-ΔlM3M2、…、ΔdM3Mn - 1-ΔlM3Mn - 1、ΔdM3Mn-ΔlM3Mn。
2.2 多端输电线路故障分支判定方法
2.2.1 端点支路故障
当故障发生在M2端的支路M2T1时,以M2为首端的故障分支判定矩阵元素小于0,ΔdM2M1-ΔlM2M1<0、ΔdM2M3-ΔlM2M3<0、ΔdM2Mn-1-ΔlM2Mn-1<0、ΔdM2Mn-ΔlM2Mnd<0,即M2端的列元素除该端交点元素为0外,其余元素都小于0。以其他端点为首端,M2为末端的故障分支判定矩阵元素大于0,ΔdM1M2-ΔlM1M2>0、ΔdM3M2-ΔlM3M2>0、ΔdMn-1M2-ΔlMn-1M2>0、ΔdMnM2-ΔlMnM2>0,即M2端的行元素除该端交点元素为0外,其余元素都大于0。根据故障初始行波的传输原理可得其他元素大于或等于0,此时得到故障分支判定矩阵为:

因此,当矩阵中某端的元素除该端交点元素为0外,其列元素全为负数,且行元素全为正数时,则判定故障发生在该端点到最近T节点的支路。
2.2.2 T节点故障
当故障发生在M1端和M2端的公共节点T1时,以M1端为首的故障分支判定元素等于0,ΔdM1M2-ΔlM1M2=0、ΔdM1M3-ΔlM1M3=0、ΔdM1Mn-1l-ΔlM1Mn-1l=0、ΔdM1Mn-ΔlM1Mn=0,即M1的列元素全部为0。同理以M2端为首端的故障分支判定元素等于0,即M2的列元素全部为0。根据故障初始行波的传输原理可得故障分支判定矩阵为:

根据矩阵元素的特征可知,矩阵中某两端的列元素全为0,且行元素全为正数时,则判定故障发生在离两端点最近的共同T节点。当故障发生在只连接一端的T节点时,如M3端的T2节点发生故障,同理可得以M3端为首的故障分支判定元素等于0,即M3的列元素全部为0。
根据故障初始行波的传输原理可得故障分支判定矩阵为:
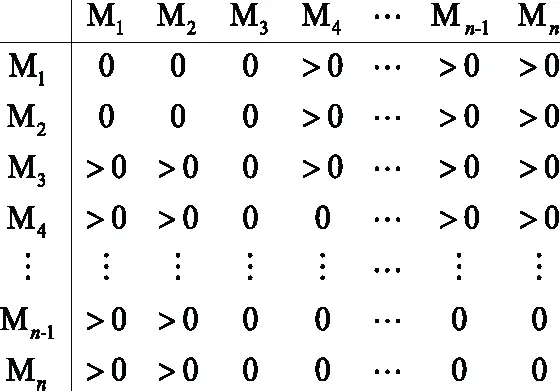
因此,当判定矩阵中所有元素为非负数,且某端点的列元素全部为0时,则故障发生在离该端点最近的T节点。
2.2.3 T节点间线路故障
当故障发生在T2节点和T3节点之间的线路时,以离T2节点最近的M3端为首端的判定矩阵元素ΔdM3M1-ΔlM3M1=0、ΔdM3M2-ΔlM3M2=0、ΔdM3M4-ΔlM3M4>0、ΔdM3Mn-1-ΔlM3Mn-1>0、ΔdM3Mn-ΔlM3Mn>0,以离T3节点最近的M4端为首端的判定矩阵元素ΔdM4M1-ΔlM4M1>0、ΔdM4M2-ΔlM4M2>0、ΔdM4M3-ΔlM4M3>0、ΔdM4M5-ΔlM4M5=0、ΔdM3Mn-1-ΔlM3Mn-1=0、ΔdM3Mn-ΔlM3Mn=0,即M3的列元素中非零元素排列顺序和M4的列元素中非零元素排列顺序相互错开。根据故障初始行波的传输原理可得故障分支判定矩阵为:

因此,当故障分支判定矩阵中各元素的特征不满足端点支路故障和T节点故障时,且相邻两列元素中非零元素的排列顺序相互错开,则判定故障发生在相邻两端点最近的T节点间线路。
考虑到实际情况中各种因素的影响,故障分支判定矩阵中各元素的数值根据文献[17]进行修正。当矩阵中某元素数值在[-300 m,300 m]时,该元素修正为0,其余元素保持不变。
故障支路确定后,取判定矩阵中故障支路对应Mn端点列元素的平均值LN,利用端点Mn到最近节点Tk的距离LMnTk与所求平均值LN的二分之一求和,得到故障点距Mn端的距离为:
(8)
2.3 多端输电线路故障定位算法
步骤1:在多端输电线路的末端安装故障行波传感器,采集故障行波信号;
步骤2:故障发生前,每条分支线路以首端点最近的T节点为分支基准,计算输电线路各分支长度的差值,得到线路固有距离差值矩阵;
步骤3:故障发生后,利用VMD-Hilbert算法提取故障初始行波波头,记录故障初始行波到达输电线路各端的时间,计算输电线路各端之间的距离差值,得到故障后线路计算距离差值矩阵;
步骤4:求故障后线路计算距离差值矩阵与故障前线路固有距离差值矩阵的差值,当某差值元素处于判定区间[-300 m,300 m]时,则该元素设定为0,其余元素不变,得到故障分支判定矩阵;
步骤5:当判定矩阵中某端点的元素除该端交点元素为0外,其列元素全为负数,且行元素全为正数时,则判定故障发生在该端点到最近T节点的支路;当判定矩阵中某端点的列元素全为0时,则判定故障发生在该端点最近的T节点处;当判定矩阵中各元素不满足端点支路故障和T节点故障特征,且相邻两列元素中非零元素的排列顺序错开时,则判定故障发生在相邻两端点最近的T节点间线路;
步骤6:故障支路确定后,取判定矩阵中故障支路对应Mn端点列元素的平均值LN,利用端点Mn到最近节点Tk的距离LMnTk与所求平均值LN的二分之一求和,得到故障点距Mn端的距离为:
3 仿真分析
在ATP/EMTP中搭建一条如图2所示的220 kV五端输电线路,输电线路参数如表1所示,在距线路M2端79.9 km处的M2T1支路、线路T2节点、距线路M2端100 km处的T1节点和T2节点间线路模拟故障,采样频率为10 MHz,2 μs后发生故障。

图2 某220 kV输电线路仿真模型

表1 输电线路参数
根据线路参数,计算得到故障前输电线路固有距离差值矩阵为:


图3 故障初始行波到达各端的时间
故障发生后,通过行波传感器获取线路各端的故障行波信号。将M1端采集的故障行波信号进行凯伦布尔变换,得到线模分量,利用VMD-Hilbert算法提取故障行波信号到达各端点的时间。限于篇幅,本文仅列出各故障点发生AB两相接地故障的情况,如表2所示。其中图3表示线路M2T1支路距M2端79.9 km处发生AB两相接地故障时,故障初始行波到达各端点的时间。
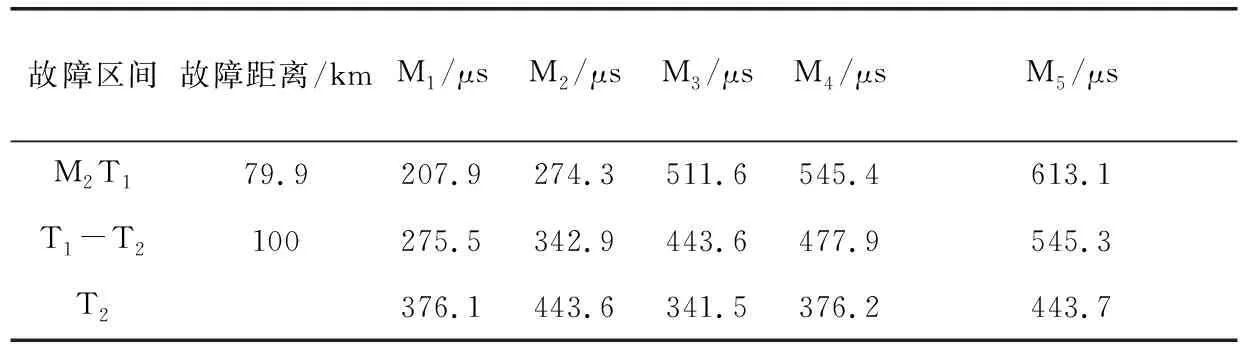
表2 故障初始行波信号到达各端的时间
3.1 端点线路故障
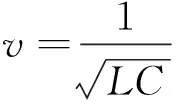
将故障后线路计算差值矩阵与故障前线路固有长度差值矩阵相减,当矩阵元素在判定区间[-300 m, 300 m]时,该元素设定为0,其它元素不变。得到故障支路判定矩阵为:

当判定矩阵中某端点的元素除该端交点元素为0外,其列元素全为负数,且行元素全为正数时,则判定故障发生在该端点到最近T节点的支路。判定矩阵中M2端点除交点元素为0外,其列元素全为负数,且行元素全为正数,判定故障发生在M2T1。此时故障点到M2端的距离为:
故障分支判定准确,定位误差为69 m。
3.2 T节点故障
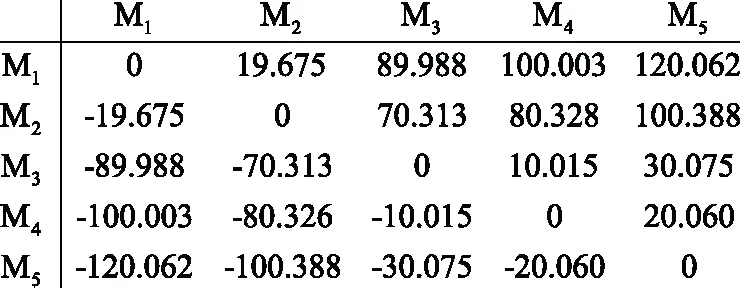
如图2所示,分析AB两相接地故障发生在线路T2节点,由表2可知故障行波分别到达各端的时间为tM1=376.1 μs、tM2=442.9 μs、tM3=341.4 μs、tM4=375.7 μs、tM5=443.1 μs,利用波速计算公式可得故障行波传输速度为2.963 04×105km/s,同理可得故障分支判定矩阵为:
当判定矩阵中某端点的列元素全为0时,故障发生在该端点最近的节点T处。判定矩阵中M3的列元素均为0,因此故障发生在M3端点最近的T2节点处,此时故障点到M3端的距离为:
符合精确定位的标准。
3.3 T节点间线路故障
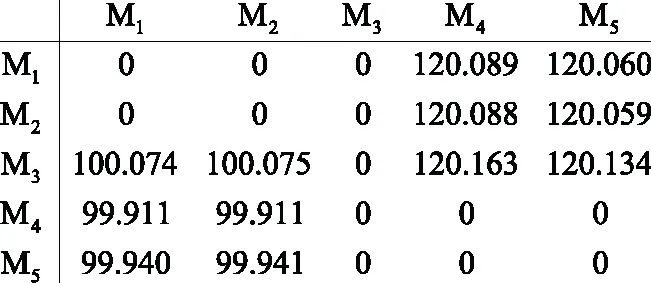
如图4所示,分析AB两相接地故障发生在线路节点T1和节点T2之间距M2端100 km处。由表1可知故障行波分别到达各端的时间为tM1=275.5 μs、tM2=342.9 μs、tM3=443.6 μs、tM4=477.9 μs、tM5=545.3 μs,利用波速计算公式可得故障行波传输速度为2.963 04×105km/s,同理可得故障分支判定矩阵为:

当判定矩阵中相邻两端点的两列非0元素排列顺序相反时,故障点发生在相邻两端点最近的T节点之间。判定矩阵中M2与M3相邻两端点的两的非0元素排列顺序相反,因此故障发生在M2端点最近的T1节点和M3端点最近的T2节点之间,故障点距M2端点的距离为:

为验证本文所提方法的准确性,在图2模型中,运用本文所提方法和HHT算法计算不同故障类型下多端输电线路的故障定位结果,如表3和表4所示。
通过比较可知,两种方法不受故障类型影响,均能有效判定故障支路,实现多端输电线路的故障定位。相比于HHT算法的定位结果,本文所提方法具有更高的定位精度。
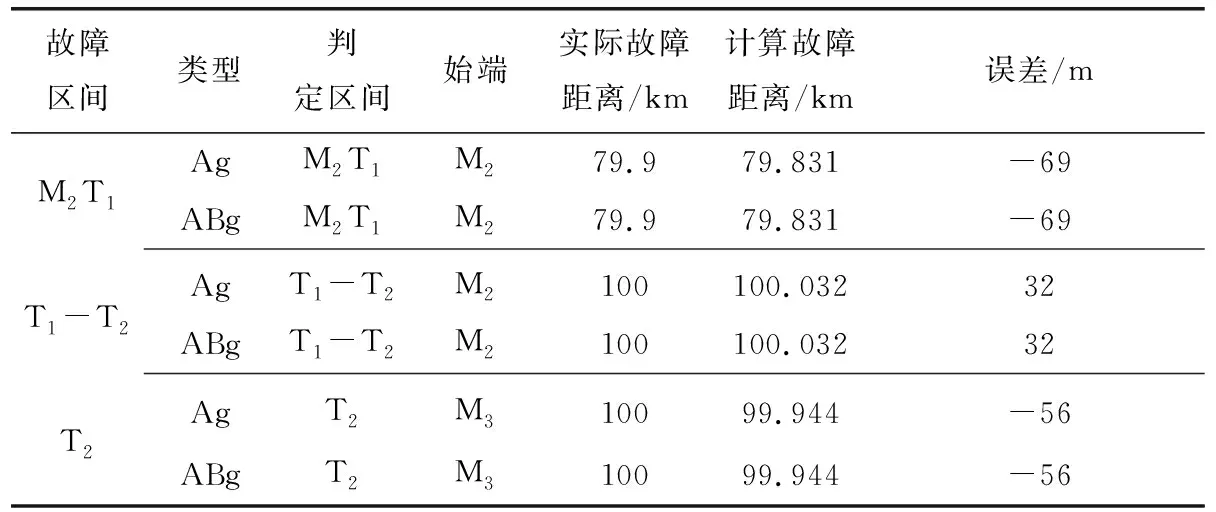
表3 本文所提方法的定位结果
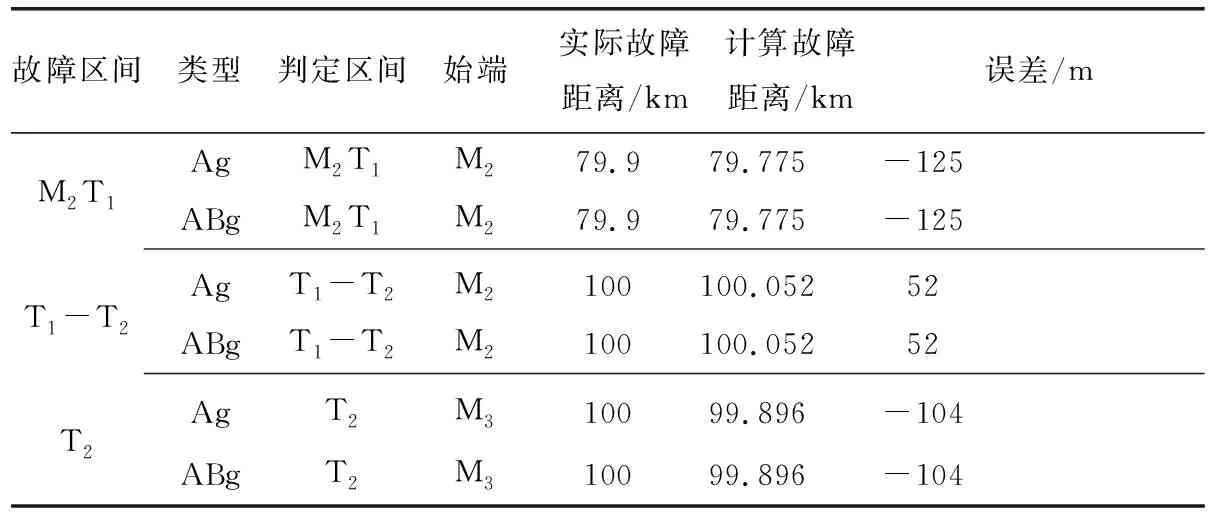
表4 HHT所提方法的定位结果
4 结束语
针对HHT检测方法中存在端点效应和模态混叠现象的问题,提出一种基于VMD算法和Hilbert变换的检测法。通过VMD算法对采集的故障初始行波信号进行模态分解,然后利用Hilbert变换进行行波到达时间的标定。
针对多端输电线路故障定位的难题,提出一种基于故障分支判定矩阵的定位算法。通过定义故障前和故障后多端输电线路距离差值矩阵,利用VMD-Hilbert算法检测故障初始行波到达各端的时间,建立故障分支判定矩阵,然后判别故障支路,最后根据故障分支判定矩阵中端点列元素计算故障点位置。
仿真结果表明,所提的检测方法能够解决HHT变换中的端点效应和模态混叠现象,实现故障行波的准确检测。所提多端输电线路定位算法能够有效判定故障支路,实现故障精确定位。相比于HHT检测方法下的定位方法,进一步提高了故障定位精度。
