区域配电网实时状态估计器及其性能分析

庞凯元，乐健，李星锐

(武汉大学 电气工程学院，武汉 430072)

0 引 言

为满足降低环境污染、实现能源可持续发展的要求，光伏、风电等分布式电源(Distributed Generation, DG) 接入运行已成为区域配电网未来的必然发展趋势[1-2]。由于出力的很强波动性和随机性，分布式电源并网后会给区域配电网带来电压闪变、电压波动和电压不平衡等诸多不利影响[3-4]，也给区域配电网的电压测量和状态估计带来新的困难和挑战。

传统配电网状态估计[5-6]是根据较多且冗余的量测数据求解出正确而完整的实时网络状态，从而实现剔除不良数据、监视网络运行状态、量测系统分析和配置优化等功能。为了应对分布式电源接入和测量装置数量有限的情况，文献[7]在假定馈线末端节点电压最低的条件下，基于电压-无功敏感度，控制分布式电源的无功功率，从而实现电压调节。文献[8]提出一种计及分布式电源的配网抗差状态估计方法，使估计值更为精确。文献[9-10]在未给分布式电源配置测量装置的条件下，将各节点负荷和分布式电源功率作为状态量进行状态估计。文献[11]提出一种基于贝叶斯理论的区域配电网状态估计器，在给定各节点功率统计信息的条件下，利用较少测量装置进行状态估计，具有较高的估计精度。

文中设计了一种基于贝叶斯理论的区域配电网状态估计器，首先依据前推回代潮流计算方法建立了配电网电压估计模型，应用贝叶斯理论设计了状态估计器，理论分析了改变监测装置位置和利用不同监测装置信息估计节点电压的影响。通过在IEEE 33节点配电系统仿真验证了文中所提出方法的正确性和有效性。进一步仿真分析了节点注入功率波动方差和测量装置位置对估计精度的影响，给出了监测装置的位置优化结果。

1 区域电网电压估计模型

在树状配电网络中，节点i与其父节点j的电压有效值及相位角之间的关系为：

(1)

(2)

式中Pji和Qji分别为节点j注入馈线段ji的有功和无功功率；Rji和Xji分别为馈线段ji的电阻和电抗；Vj和Vi及θj和θi分别为节点j和节点i的电压有效值及相位角。

忽略馈线段上的功率损耗，认为式(1)和式(2)等号右边的电压有效值为1.0 p.u.，可得到：

(3)

(4)

式中Ci是以节点i为根节点的最大生成树；Pk和Qk指从节点k流出的有功无和无功功率。

对配电网中除根节点(0号节点)外的其他N个节点列写与其父节点电压有效值和相角的差值为：

(5)

式中节点fi是节点i的父节点；S=[P1P2…PnQ1Q2…Qn]T是N个节点的流出有功功率和无功功率；Zn是根据潮流方程得到的阻抗矩阵，其形式如下：

(6)

式中R和X是N阶对角阵，其对角元素rkk和xkk是节点k与其父节点馈线上的电阻和电抗；P是根据网络拓补形成的N阶矩阵，其元素pij=1当且仅当节点j∈Ci，否则pij=0。

2 状态估计器的设计

2.1 估计器表达式

在包括根节点在内的M个节点放置监测装置，则有测量装置节点的电压有效值和相角的差值为：

(7)

式中Pm和Zm是2(M-1)×2N阶矩阵。

同理，剩余N-M+1个无监测装置节点的电压有效值和相角的差值为：

ΔVe=PeΔV=PeZnS=ZeS

(8)

式中Pe和Ze是2(N-M)×2N阶矩阵。

根据贝叶斯理论[11]，无监测装置节点电压估计器表达式为：

(9)

式中μS是功率矩阵S的均值；∑S是功率矩阵S的方差。

2.2 不同监测信息的影响

式(9)所示估计器可改写为：

(10)

设监测装置数量和安装位置不变，现利用不同监测值差值组合进行估计，即ΔVe不变而ΔVm中的节点差值组合变化。取另一个节点差值组合不同于ΔVm的包含M个有监测装置节点电压有效值和相角的ΔVm1矩阵，ΔVm1和ΔVm的关系为：

ΔVm1=Am1ΔVm

(11)

式中Am1是2(M-1)阶方阵，由于ΔVm1和ΔVm都包含M个有监测测量节点电压有效值和相角，Am1中行向量线性无关，故Am1可逆。

根据式(7)可得：

Zm1=Am1Zm

(12)

由式(10),此时估计器为：

(13)

将式(12)代入式(13)右边可得：

Ze(μs+∑S(Am1Zm)T[(Am1Zm)∑S(Am1Zm)T]-1·

(Am1ΔVm-Am1ZmμS))

( ΔVm-ZmμS))

可以看出，选取不同有监测装置节点差值组合的ΔVm，ΔVe的表达式不变。因此在监测节点数量和位置相同的情况下，采用不同监测装置的测量值差值组合不影响对其他无监测装置节点电压的估计。

类似的，在ΔVm矩阵不变而ΔVe中节点差值组合改变的情况下，任意选取一个包含N-(M+1)个待估计节点电压有效值和相角的矩阵ΔVe1，ΔVe1与ΔVe的关系为：

ΔVe1=Ae1ΔVe

(14)

式中Ae1是2(N-M)阶方阵，由于ΔVe1和ΔVe都包含N-(M+1)个预测节点电压有效值和相角，Ae1中的行向量线型无关，故Ae1可逆。

根据式(8)，可以得到：

Ze1=Ae1Ze

(15)

此时，根据式(10)，估计器的表达式为：

(16)

将式(14)和式(15)代入式(16)，得到：

(17)

由于Ae1可逆，消去Ae1得到：

(18)

从式(18)可以看出，选取不同无监测装置节点差值组合的ΔVe矩阵，估计器的表达式不变，式(16)和式(10)完全等价；因此在监测节点数量和位置相同的情况下，采用不同无监测装置节点的差值组合构成ΔVe矩阵，同样不影响对其他无监测装置节点电压的估计。。

3 仿真及性能分析

文中选用如图1所示的IEEE 33节点配电网络作为目标系统，利用MATLAB进行仿真计算，计算结果以标幺值表示。

图1 IEEE 33节点配电系统

设首端节点(0号节点)电压保持不变，各节点流出有功功率和无功功率符合高斯分布N(μ,σ2)，其中σ=0.3μ。

用节点最大绝对误差(Absolute Error, AE)和平均均方根误差(Average Root Mean Square Error, ARMSE)两个指标对估计器性能进行评价。最大绝对误差定义为：

(19)

3.1 节点功率方差的影响

在节点编号为0、16、20、23和31的节点放置电压监测装置且位置不发生改变；设网络中存在一个功率方差较大(σ=1.0μ)的节点，改变该节点的位置， 5 000次蒙特卡罗仿真后后编号6-17节点电压的最大绝对误差及平均均方根误差如表1所示。

由表1可以看出，当网络中节点功率方差增大时，电压有效值和相角估计精度均下降。节点6-17中，若段首节点(如节点6或7)或段末节点(如节点16或17)负荷功率的方差较大，AEmax和ARMSE均较大，估计器性能降低；而段中部节点(如节点7-15)负荷功率方差较大时，对估计器性能的影响很小，估计器具有较高的精度。因此，在同一馈线段(指网络中度大于1的两个节点之间的一段线路或度大于1的节点到叶子节点的一段线路，其特征是除段首和段末节点，其余所有节点的度为1)中，应避免段首或段末节点的功率方差较大，必要时可以改变网络结构。

同时也可以看出，即使在节点功率方差较大的节点(如节点16)放置监测装置，也不能有效提高估计精度。

表1 节点功率方差对估计精度的影响

3.2 监测装置位置的影响

选取5个节点放置监测装置，其中0、2、7、15号节点的监测装置不变，最后一个监测装置依次放在25-32号节点上，在节点功率方差保持不变(σ=0.3μ)时，5 000次蒙特卡罗模拟后的最大绝对误差及平均均方根误差如表2所示。

由表2可以看出，估计误差最大的节点容易出现在馈线段的末端(如节点24和32)，为降低馈线段末端节点的估计误差，可将监测装置放置在靠近馈线段末端的节点上，同时降低总体的估计误差。

此外还可以看出，在电压有效值估计中，监测装置放置于29号节点上时，32号节点的估计误差较大，而放置于30号节点上时则该节点电压有效值的估计误差有明显降低。表明离监测节点距离越远的节点电压有效值的估计误差越大。仿真结果表明该结论具有普遍性。

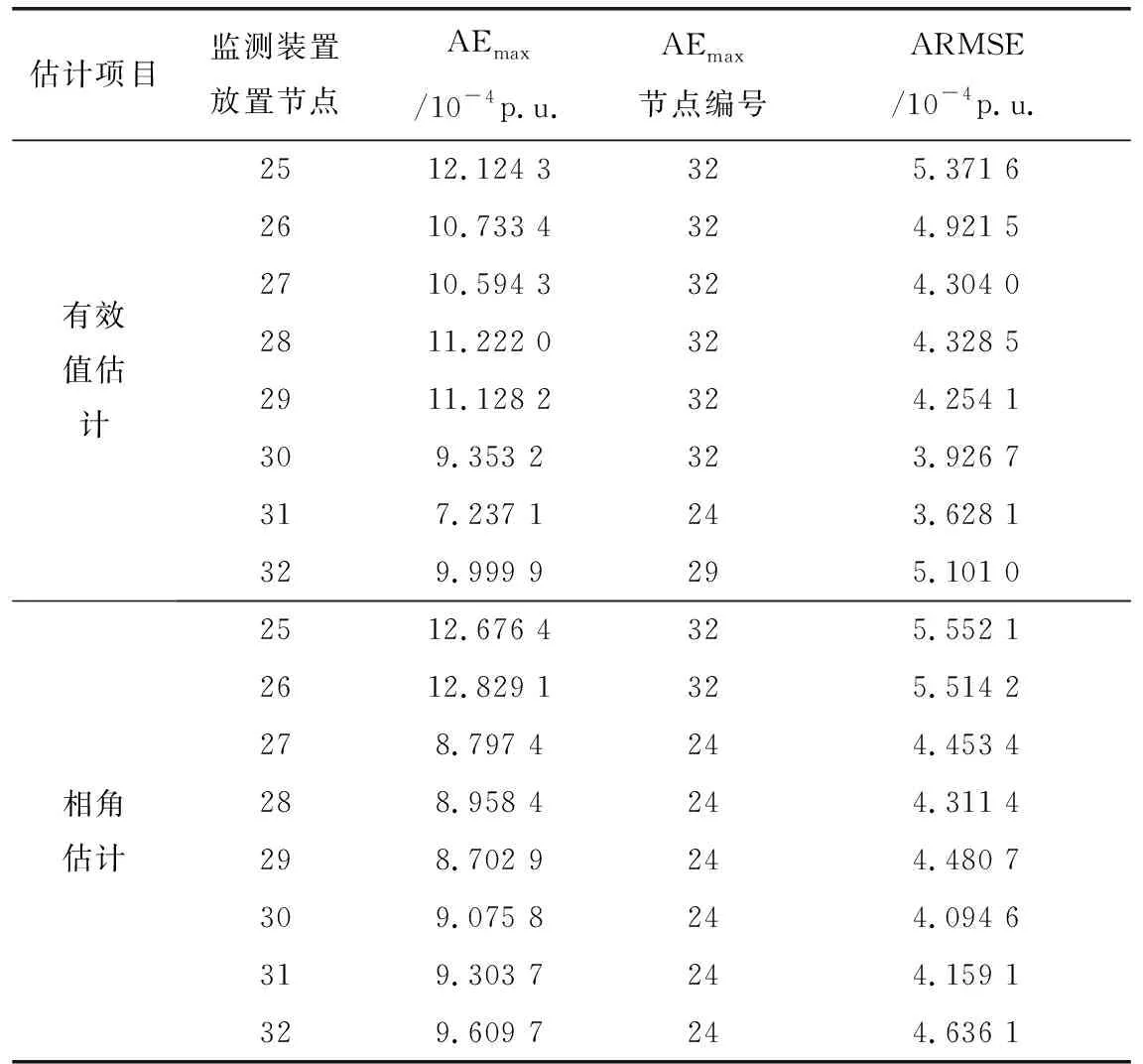
表2 监测装置放置位置不同对估计精度的影响

3.3监测装置放置位置的优化

利用粒子群算法[12-13]，在IEEE 33节点配电网络中计算不同监测节点数量下的监测装置最优放置位置， 5 000次蒙特卡罗仿真后的结果如表3所示。

表3 监测装置数量不同的最优放置位置

在监测装置处于最优放置位置的条件下，得到有效值和相角估计的ARMSE随监测装置数量的变化曲线如图2所示。

图2 ARMSE随监测装置数量的变化曲线

由表3和图2可以看出，随着监测装置数量的增加，估计器的ARMSE下降；当监测装置数量达到7个时，ARMSE随着监测装置数量的增加下降不明显，存在饱和现象。

4 结束语

文中设计了一种基于贝叶斯理论的区域配电网状态估计器，以提高实时监测装置有限且分布式电源出力预测偏差时的配电网状态估计精度。IEEE 33节点配电系统的仿真结果表明，区域配电网中馈线段首端或末端附近节点功率方差较大时，估计器的误差较大；在馈线段末端附近放置监测装置可以有效限制馈线段的估计误差；状态估计器的估计误差随监测节点数量的增加呈指数形式下降，存在饱和现象。