三相四桥臂并网逆变器的无差拍重复控制
2018-09-27谭翠兰陈启宏张立炎周克亮
谭翠兰, 陈启宏, 张立炎, 周克亮
(1. 武汉理工大学自动化学院, 湖北省武汉市 430070; 2. 江汉大学物理与信息工程学院, 湖北省武汉市 430056)
0 引言
逆变器作为分布式发电单元与电网的接口,能否为电网注入优质电力直接影响发电系统的质量与效率。为保证电网质量不受影响,逆变器要尽量减小并网电流的总体谐波畸变率(THD)。在各种拓扑结构的并网逆变器中,三相四桥臂的LCL型并网逆变器由于具备能有效滤除谐波、直流电压利用率高等优点得到广泛应用[1-3]。
目前,并网逆变器的主要控制策略有滞环控制、比例—积分(PI)控制、比例—谐振(PR)控制等。滞环控制跟踪精度低且要求采样频率高,传统的PI控制方法受到带宽的影响对交流信号的跟踪精度不高,谐波抑制能力较差。PR控制在谐振频率处具有无穷大的开环增益,理论上能对频率为谐振频率的正弦信号实现零稳态误差控制,但多谐振控制计算复杂且在离散化时对参数敏感,在并联的谐振项数目较多时难以设计相角补偿,而基于内模原理的重复控制器相当于比例、积分和多个谐振控制器的并联,可以抑制各次谐波,能够在基频及其整数倍的频率处提供高增益,理论上能实现对正弦电流的无静差控制[4-6],但单一的重复控制器动态性能差。随着微处理器的发展,基于数字控制的无差拍控制算法获得了快速发展。
无差拍电流控制是指在每一开关周期内,根据被控对象的数学模型和当前时刻的采样值,推导下一时刻脉宽调制(PWM)参考输入电压,通过三维空间矢量调制(3D-SVM)[7]控制各桥臂开关管的占空比输出,从而获得下一时刻的并网电流。无差拍电流控制动态响应快,但控制算法依赖于被控对象的数学模型,控制性能易受电路参数波动影响,且存在稳态误差[8-14]。文献[9]为尽可能消除控制延时带来的误差,用算术平均值预测电流偏差,将i(k)与i(k+2)直接建立联系,虽然简化了计算过程,但对低次谐波的抑制效果不够理想。文献[10]提出了一种改进的加权电流平均控制的无差拍控制方法,并将电网电压前馈补偿加到平均电流参考值中以减小稳态电流跟踪误差,实际上文中的无差拍算法也是根据电感按一阶系统建模,文中并网电流的THD受电网电压影响较大。文献[11]针对三相四桥臂的离网逆变控制采用无差拍加重复控制算法,并采用二阶巴特沃斯低通滤波器对逆变电压进行滤波处理,通过重复控制器对谐波进行补偿,使得离网模式的电压THD仅有0.5%。文献[12]针对四桥臂的离网逆变器,采用考虑中线电感的无差拍预测控制,但在模型参数变化时会增大稳态误差。
为简化控制算法并消除延时带来的误差,本文在传统无差拍控制器中嵌入重复控制器,结合二者优势,可实现对并网电流的快速准确跟踪,有效降低了并网电流THD含量。根据系统对象模型推导了最佳补偿拍数,并从理论分析角度给出了改进重复控制器的参数设计方法。最后,通过Simulink仿真和在一台10 kW三相四桥臂并网逆变器上的实验验证了所提控制策略的有效性。
1 三相四桥臂并网逆变器的模型拓扑图
典型的三相四桥臂并网逆变器如图1所示,它是在传统的三桥臂基础上增加了一个半桥电路以控制中点电压,从而产生三相独立的电压。由于三相之间不存在耦合关系,可使用3个独立的电流闭环控制器来控制各相电流[15]。
图1中,Udc为直流母线电压;Q1至Q8为绝缘栅双极型晶体管(IGBT)大功率开关管;Lf为逆变器侧电感;R1为电感Lf的等效内阻;Lg为并网侧电感;R2为电感Lg的等效内阻;Cf为滤波电容;R为滤波电容串联电阻。锁相环(PLL)在每个采样周期实时检测当前电网电压相位θ,根据相位角计算出与电网电压同相位的并网电流给定值i*,控制器通过比较当前给定电流与实际并网电流的偏差,推导出下一时刻PWM的控制量vj,ref(j=a,b,c),经3D-SVM后获得占空比输出来控制开关管IGBT的通断,从而获得下一时刻的并网电流。
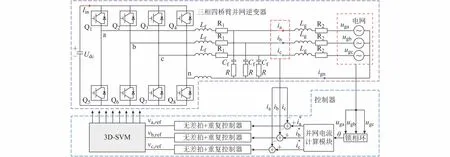
图1 三相四桥臂并网逆变器结构Fig.1 Structure of a grid-connected three-phase four-leg inverter
滤波电路采用LCL结构不仅可以有效减小总滤波电感,而且具有很强的高频谐波抑制能力,由于LCL型滤波器是三阶系统,其动态模型中存在高频谐振峰,不利于控制系统的稳定,通过在滤波电容支路上串联适当阻值的电阻R可以有效抑制谐振峰,提高系统的稳定性[16]。本文LCL型三相四桥臂并网逆变器主电路的相关参数见附录A表A1。
图1中,LCL滤波器电容用于吸收高次谐波,考虑中低频模型时可将其忽略,用于控制的模型正是中低频模型,因此,将LCL型滤波器简化为一阶系统[17-18],建立三相四桥臂并网逆变器的控制模型如下:
(1)
式中:ua,ub,uc为逆变器的三相输出电压;uga,ugb,ugc为三相电网电压;ia,ib,ic为三相并网电流。
2 控制器设计
2.1 无差拍控制
根据式(1),状态方程描述如下:
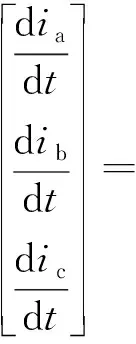
(2)
式中:ia,ib,ic为状态变量。
将式(2)离散化,选择采样周期为Ts,下一时刻并网电流的离散状态方程为:
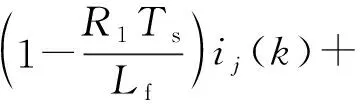
(3)
式中:j=a,b,c。
如果在一个采样周期内实现了并网电流对给定参考电流的无差跟踪,则认为达到了无差拍的控制效果[9],即
i(k+1)=i*(k)
(4)
式中:i(k+1)为k+1时刻电流采样值;i*(k)为k时刻电流输入的给定值。无差拍控制的闭环传递函数H(z)=z-1,这样无差拍电流控制器理论上是差一拍(即一个采样周期)的控制延时,从而能够提供快速的动态响应。
三相并网逆变器的PWM电压可描述为:
Uj(k)=UdcSj
(5)
式中:Sj为开关管占空比。
将式(4)、式(5)代入式(3)可得到无差拍控制的开关管占空比输出为:
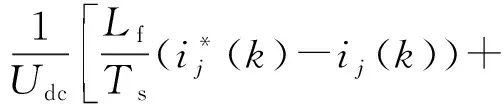
(6)
无差拍控制的结构框图如附录A图A1所示,其中Gp(z)为被控对象的传递函数。
如果忽略附录A图A1中逆变侧电感内阻,采用零阶保持器将被控对象离散化,采样周期为Ts,考虑到数据采样及PWM控制延时,设延时函数HD(s)=e-sTd,其中Td为延迟时间,得到附录A图A2所示的控制框图。
附录A图A2中,K为控制算法中的电感值和实际电感值的比,采用零阶保持器离散化被控对象,得到:
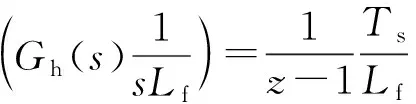
(7)
如果不考虑滞后一拍和采样及控制延时,则系统的闭环传递函数为:
(8)
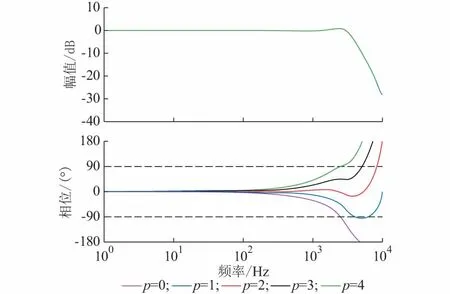
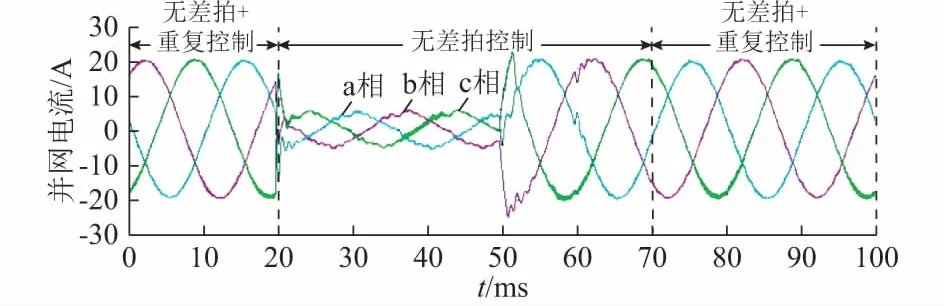
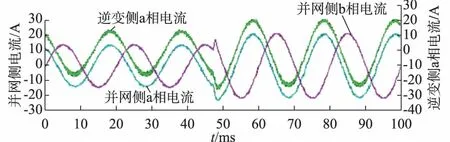
若要闭环系统的极点落在单位圆内,可求得使系统稳定的K的取值范围为0 (9) 采用双线性变换,得到闭环系统特征方程为: Kω2+(2-2K)ω+2+K=0 (10) 利用劳斯判据可得,使系统稳定的K的取值范围为:0 如果考虑更多拍数的控制延迟,对于延时函数HD(s)=e-sTd,采用一阶泰勒展开得: (11) 若延迟时间Td与离散化采样周期Ts满足:m=Td/Ts,其中m∈N,采用双线性变换,则延时函数HD(s)的z变换可表示为: (12) 则附录A图A2所示系统的离散开环传递函数为: G=G1(z)z-1HD(z)Gp(z)= (13) 式中:m为数据采样及控制延迟的拍数。 考虑m的取值为0至6时,根据离散开环传递函数画出一组根轨迹图如图2所示。 图2 离散z域带延时的无差拍控制根轨迹Fig.2 Root locus of deadbeat control with delay in z-plane 无差拍控制以其响应快、控制精度高的优点广泛应用于PWM并网逆变器中,但由于信号采样及数字计算等会导致数字延迟[19]。图2给出了在延时拍数m取不同值时,预测电感系数K的取值上限。在离散z域中,为使系统保持稳定,极点必须落在单位圆内,从图2中可以看出,随着延迟拍数m的增加,使系统稳定的无差拍控制中预测电感的系数K的取值上限变小,说明控制延时影响系统稳定性。当延时拍数一定时,预测电感的系数不能超过单位圆的边界,否则系统将由稳定变为不稳定,说明模型电感参数变化时也会影响系统稳定性。 传统无差拍控制的数据采样、计算及占空比输出应该同时完成,但在实际工程应用中,由于受数据采样的影响,占空比输出会滞后于实际采样一定拍数,受延时时间Td的影响,会造成电网电流的预测误差,且无差拍控制算法中由于电感参数的波动及在各种干扰的作用下必然存在稳态误差,这种误差为周期性信号,其周期与电网基波周期一致。而重复控制能很好地消除周期性扰动,实现对正弦信号的无差跟踪,理论上将传统无差拍控制与重复控制相结合可获得快速的动态响应及零稳态误差输出。 传统无差拍控制无法抑制周期性的扰动,基于内模原理(internal model principle,IMP)的重复控制可利用误差的重复性来逐周期修正输出信号,内模原理指出,在反馈控制环节中若含有外部被控信号的数学模型,则可实现系统的零稳态误差跟踪,内模实际上可看作是一个信号发生器[20]。对并网系统而言,其谐波信号的频率是基波信号频率的倍数,而且具有周期性。对于周期为T0的信号,其内模原理结构图如附录A图A3所示,图中:T0=2π/ω0=1/f0,其中f0为信号的频率。周期性信号发生器的传递函数Grc(s)可表述如下: (14) 从式(14)可看出,Grc(s)可看作比例、积分及谐振控制之和,具有如下极点:s=±jnω0,n∈N,因此在每个谐振频率点Grc(s)趋于无穷,如果将Grc(s)包含在闭环系统中,则在谐振频率处可实现零稳态误差跟踪[21-22]。附录A图A3所示的连续域在数字控制领域不便于实现,令z=esTs,可将式(14)离散化为: (15) 式中:N=T0/Ts∈N,为系统采样频率与系统基波频率的比值。 T0为基波周期,Ts为采样周期,重复控制器传递函数Grc(z)中z-N相当于一个全通滤波器,允许各次谐波通过,引入不带相位偏移的低通滤波器Q(z)=0.25z+0.5+0.25/z可提高重复控制器的性能[6,23],引入Q(z)后重复控制器变化为: (16) 对基波周期为0.02 s的电网,当采样频率fs为20 kHz时,式(16)的幅频特性如附录A图A4所示。从该图中重复控制器的波特图可以看出,在基波及各次谐波处,重复控制器具有高增益,从而对各次谐波具有较强的抑制能力。带相位补偿的离散域重复控制框图如附录A图A5所示,其中重复控制器的传递函数可表式为: (17) 式中:Gf(z)为超前相位补偿环节;krc为重复控制器增益。 为简化实际控制系统的设计,Gf(z)常选为zp,这样式(17)可简化为: (18) 由式(18)所描述的重复控制器的结构如附录A图A6所示[24],将该重复控制器结构嵌入原控制系统中,得到如附录A图A7所示的内置重复控制器的无差拍控制结构。对于图A7所示控制系统,如果不考虑延时,则电流环的闭环传递函数为: (19) 式中:krc′=krcKLf/Ts。 如果闭环系统的特征根都在单位圆内则系统稳定,即1-(1-krc′zpGp(z))Q(z)z-N=0的根在单位圆内,得到系统稳定的充分条件为:对于所有z=ejωTs,有式(20)成立。 (20) 重复控制器增益krc对系统的稳定性和响应速度均有影响,krc越大,系统响应越快,但是选择过大会使系统变得不稳定。 补偿环节zp中超前补偿拍数的选取可通过分析被控对象闭环传递函数的性能来确定,本文系统中被控对象的等效框图如附录A图A8所示,在该等效框图中,若将电网电压ug(s)看作扰动,忽略电感内阻R1和R2,得到并网电流相对于逆变侧输入电压uinv(s)的传递函数为: (21) 式(21)为重复控制器设计时的实际被控对象,将附录A表A1中的参数代入并离散化后可得到被控对象的传递函数为: (22) 为保证系统的稳定性,根据图2所示根轨迹选取无差拍控制中系数K=0.7,保证极点落在单位圆内距圆边界一定距离,将式(22)代入,系统的闭环传递函数为: (23) 为补偿被控对象的滞后,加入补偿环节Gf(z)=zp,图3为G(z)Gf(z)带不同线性相位超前补偿拍数时的波特图,从图中可看出,超前补偿拍数不改变幅频特性,但相频特性有明显改变,超前补偿拍数分别为p=0,1,2,3,4时的系统带宽见附录B表B1。 图3 带不同补偿拍数时系统的波特图Fig.3 Bode diagram of system with different compensation steps 从图3中可以看出,当线性相位超前补偿拍数p=2时系统带宽最大,综合考虑采样及控制延时,在实际控制中选取p=3。 为验证所提控制算法的有效性,在MATLAB中按照图1构建三相四桥臂并网逆变器的拓扑图及控制器,模型参数见附录A表A1。三相四桥臂并网逆变系统的功率为10 kW,电网电压为220 V,故额定功率时输出给定电流的峰值为21.2 A。附录A图A9为采用内置重复控制器的无差拍控制算法的并网电流输出波形及快速傅里叶变换(FFT)分析。仿真结果显示:稳态时的并网电流最大值为21.09 A,接近额定功率时的给定电流峰值,并网电流THD仅为0.58%。 附录A图A10为无差拍+重复控制算法在a相电流上的误差波形,从图中可看出本文所提算法在重复控制器的作用下使误差逐周期减小,稳态时的并网电流误差可控制在0.5 A以内。 附录A图A11为在本文无差拍+重复控制算法下A相逆变侧及并网侧的仿真电流波形,可以看出简化为一阶系统建模时两者电流基本一致。 无差拍+重复控制算法的并网电流动态响应见附录A图A12,当给定电流参考值突增或突减时并网电流能很快跟随。图A12(a)中给定电流有效值从10 A突然增加到15 A,图A12(b)中给定电流有效值从15 A突然减小到10 A,动态响应时间均在0.5 ms以内。 为了验证仿真结果,采用TI公司的数字信号处理器(DSP)芯片TMS320F28335作为主控芯片,按图1搭建了一套10 kW的三相四桥臂并网逆变器的实验平台,实验电路参数与仿真参数一致,见附录A表A1。IGBT采用英飞凌公司的FF100R12RT4模块。采样模块分别有1路直流母线电压采样、3路交流电压采样及3路并网电流采样。开关管IGBT的驱动采用CONCEPT驱动模块,该模块接收DSP发来的PWM控制信号驱动IGBT,搭建的实验平台如附录A图A13所示。在实验中,验证了重复控制补偿环节zp(p=0,1,2,3,4)可对相位进行超前补偿。 实验中采用锁相环实时检测电网电压相位,利用DSP的PWM通道输出锁相角θ的斜坡函数,电网电压a相及锁相角θ的输出波形见附录A图A14,可以看出,锁相角的最大值与电网电压最大值一致,这样可保证并网电流与电网电压同频同相。 附录A图A15(a)和(b)分别为采用单独无差拍控制和无差拍+重复控制算法时a相电压和电流的相位对比图,图A15(b)为重复控制补偿3拍的控制效果。可以看出,单独无差拍控制下,电流滞后电压一定相角,图A15(b)内置重复控制算法后通过重复控制的超前相位补偿使得并网电流与电网电压无相位差。 附录A图A16(a)和(b)分别为采用本文所提控制算法的三相并网电流波形及FFT分析,在稳态时基波电流最大值达到21.18 A,本文图A16(a)中在电网电压THD达到2.16%的情况下,并网电流的THD可下降到1.23%,文献[10]的图15在投入控制算法后并网电流THD为1.78%;本文在电网电压正弦度差于文献[10]中图22的电网电压时,并网电流的波形正弦度仍要优于文献[10]中图24的稳态并网电流。 为验证本文所提控制算法的动态响应性能,图4给出了当额定电流从15 A降到1 A,维持30 ms再突变到15 A的动态响应图,可以看出当给定电流发生突变时电流能够快速响应。15 A时采用无差拍+重复控制算法,降到1 A时采用无差拍算法,由于重复控制存在一个基波周期延时,由1 A跳变到15 A时的第一个基波周期重复控制算法不起作用,经过一个基波周期后重复控制算法投入使用,可以看出在投入重复控制后电流波形正弦度更好,电流振荡消失,波形变得更光滑。 图4 并网电流动态响应Fig.4 Dynamic response of grid-connected current 为简化控制,将被控对象的模型由LCL型滤波器简化为一阶系统进行控制,使得无差拍控制算法变得简单,避免了复杂的高频建模,同时嵌入重复控制对周期性误差进行抑制。图5显示了动态响应时逆变侧a相及并网侧a相和b相的电流波形,可以看出逆变侧与并网侧电流基本一致,也在实验上验证了简化控制是可行的。 图5 逆变侧a相和b相电流及并网侧a相电流波形Fig.5 Waveforms of phase a current on inverter side and phase a and phase b currents on grid side 通过在10 kW三相四桥臂并网逆变器上进行实验验证,将本文所提控制算法与文献[10]控制算法相比较,可以看出本文所提无差拍+重复控制算法的并网电流更光滑,THD含量更低,且通过重复控制器的超前线性相位补偿环节zp可使并网电流与电网电压无相位差。 本文针对三相四桥臂并网逆变器提出了一种内置重复控制器的无差拍预测算法,分析了无差拍预测算法中延时对预测电感值的影响,并利用根轨迹给出了预测电感系数的取值范围。无差拍控制具有快速的动态响应,为了进一步消除周期性干扰,将重复控制器嵌入到无差拍控制算法中可减小稳态误差,有效降低并网电流的THD含量。本文研究的算法并未考虑电网频率波动的情况,下一步工作将进一步研究频率自适应分数阶重复控制在并网逆变器中的应用。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
2.2 重复控制器设计

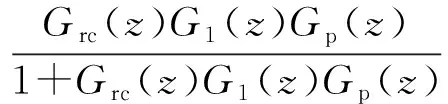
3 系统仿真分析
4 实验结果分析
5 结语
