三相并网逆变器频率耦合机理分析及稳定性判定

2018-09-27邹小明王国宁杨友耕籍勇亮

电力系统自动化 2018年18期

关键词：奎斯特扰动耦合

邹小明, 杜雄, 王国宁, 杨友耕, 籍勇亮

(1. 输配电装备及系统安全与新技术国家重点实验室(重庆大学), 重庆市 400044; 2. 国网重庆电力公司电力科学研究院, 重庆市 401123)

0 引言

目前分布式发电技术的发展使得并网逆变器广泛应用于电力系统中[1-2]。逆变器和电网之间相互作用可能会引起稳定性问题[3-4],威胁到分布式发电系统的安全可靠运行。因此,分析并网逆变器系统的稳定性非常重要。

基于阻抗判据的方法广泛应用于分析互联系统的稳定性。阻抗判据方法最先由Middlebrook提出[5],并已广泛应用于分析直流互联系统的稳定性[6-7]。

在三相交流系统中,由于系统不存在固定的直流静态工作点,因而不能采用传统小信号建模方法直接建模[8]。为此,文献[9]提出了在旋转坐标系下建立并网逆变器阻抗模型的方法。该方法通过Park变换将三相交流量变换成dq坐标系下的直流量,然后在其直流静态工作点上进行小信号线性化,得到dq坐标系下的并网逆变器阻抗模型。由于dq坐标系下的阻抗模型物理意义不清晰,且难以测量,后来学者又普遍采用了基于谐波线性化的谐波阻抗建模方法[10-12]。该方法直接在静止坐标系下建立三相交流系统中变流器阻抗模型,因此物理意义清晰,非常便于测量。

文献[13-14]在静止坐标系下建立了逆变器在正负序扰动频率下的谐波导纳模型。文献[13]中的模型忽略了正负序频率分量相互耦合的影响,因而在某些情况下不能准确判定出并网逆变器系统的稳定性。文献[14]则考虑了这一频率耦合因素进行建模分析,弥补了文献[13]中的不足。

但是利用文献[14]中建立的逆变器耦合导纳模型不得不采用广义奈奎斯特判据才能判定并网逆变器系统的稳定性。而采用广义奈奎斯特判据,稳定性判定过程复杂,且不便于给出系统的稳定裕量,指导逆变器控制器设计。另外,文献[13-14]中并未揭示清楚系统中两个频率分量的耦合机理。

文献[15-16]在同步旋转坐标系下建立了逆变器等效阻抗模型。虽然得到的dq阻抗模型中不存在两个频率相互耦合的问题,但是d轴分量和q轴分量会相互耦合,因此也必须采用广义奈奎斯特判据判定并网逆变器系统的稳定性。

文献[17]为避免采用广义奈奎斯特判据判定并网逆变器系统的稳定性,在极坐标系下定义了逆变器广义阻抗模型和电网广义阻抗,基于所定义的广义阻抗,采用奈奎斯特判据对系统稳定性进行了分析。但该文中定义的广义阻抗不具有明确物理意义,也难以测量。

并网逆变器系统中dq轴控制器结构或参数的不对称,会导致系统在静止坐标系下存在两个扰动频率分量相互耦合,且这两个耦合频率满足ωp和2ω0-ωp的关系[18](ωp和ω0分别表示原始注入扰动角频率和基波角频率),而不是文献[13-14]中所表述的正负序频率相互耦合。文献[18]进一步指出:静止坐标系下的频率耦合阻抗模型[14]和同步旋转坐标系下的dq轴耦合阻抗模型[16]具有等价性,相应地,利用两类模型采用广义奈奎斯特判据判定出的系统稳定性结果也是一致的。

本文首先揭示了并网逆变器系统中两个频率分量的耦合机理,弥补现有文献的不足。在此基础上分析得到了能够分别表征并网逆变器系统在ωp和2ω0-ωp频率下的稳定特性的两个逆变器等效导纳,利用这两个导纳采用奈奎斯特判据即可判定出系统的稳定性,无须采用广义奈奎斯特判据。相比现有采用广义奈奎斯特判据的方法,本文采用奈奎斯特判据判定系统的稳定性,判稳过程简单,且能给出系统的稳定裕量,指导逆变器控制器设计。

1 并网逆变器的频率耦合机理

本文具体研究对象为如图1所示的三相并网逆变器。图中:Vdc为直流侧电压(为恒定不变值)；vga,vgb,vgc为三相理想电网电压；Zg为电网阻抗。公共连接点(PCC)三相电压表示成vabc(幅值为V1),电压、电流采样滤波环节分别用Gfv和Gfi表示。

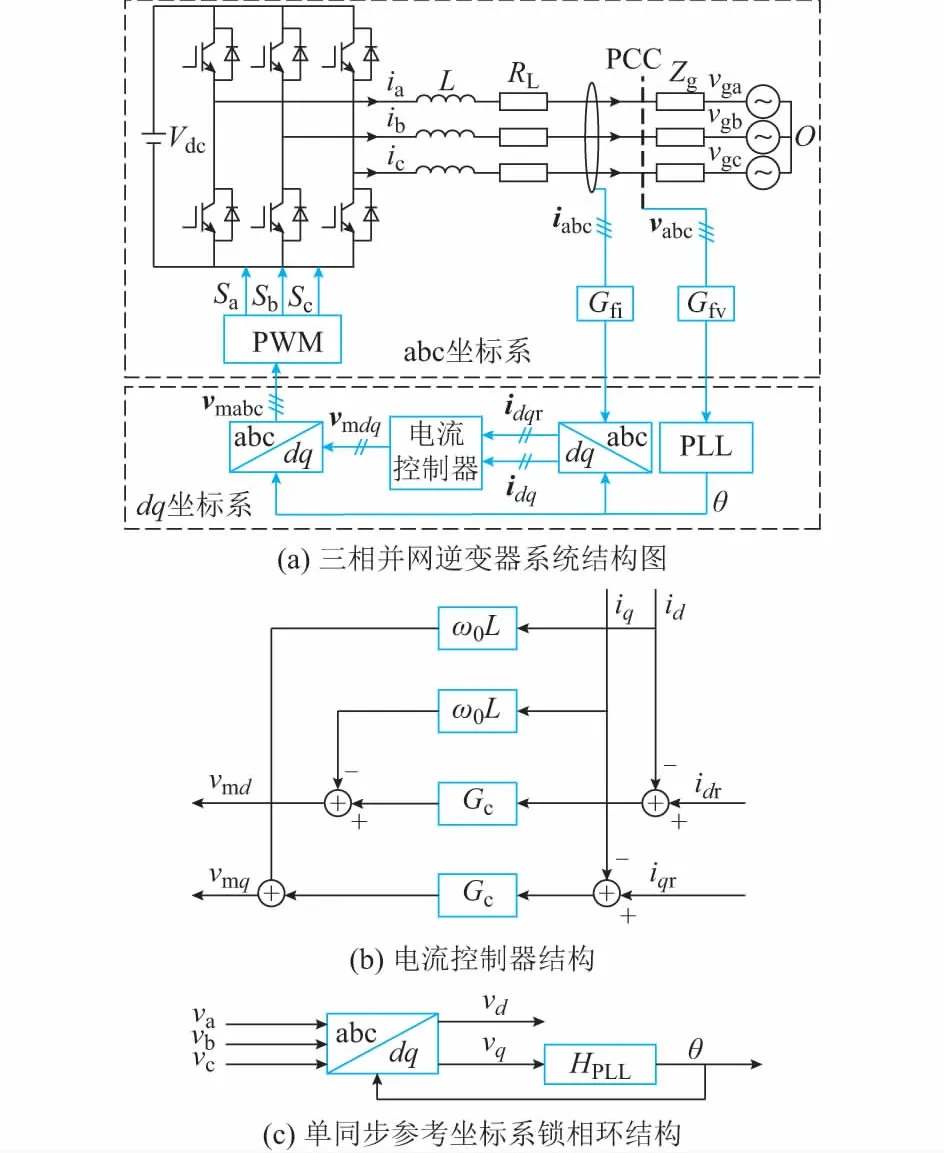
图1 三相并网逆变器系统Fig.1 Three-phase grid-connected inverter system

图1中显示的三相并网逆变器系统由两部分构成,在abc坐标系下实现的功率电路、采样、调制环节和在dq坐标系下实现的控制器部分。电流控制器采用图1(b)所示结构。锁相环结构如图1(c)所示。图中Gfv,Gfi,Gc,HPLL的表达式为:

(1)

(2)

(3)

式中:τf为电流电压采样滤波的时间常数;kp和ki分别为电流控制器中的比例参数和积分参数;kpp和kpi分别为锁相环中的比例参数和积分参数。

1.1 单扰动频率输入、双扰动频率输出特性表征

从上述分析中不难发现,dq轴结构不对称的锁相环使得逆变器对扰动信号表现出单频率输入、双频率输出特性。参考文献[19]中的逆变器导纳建模方法,得到ωp频率的三相对称扰动输出电流与ωp频率的三相对称扰动输入电压满足关系式(4);2ω0-ωp频率的三相对称扰动输出电流与ωp频率的三相对称扰动输入电压满足关系式(5),即式(4)和式(5)表示的两个解析表达式YSA和YAA能够表征逆变器中三相交流侧单频率扰动电压输入、双频率扰动电流输出的特性。

(4)

(5)

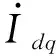
(6)

1.2 两个频率相互耦合机理分析

(7)

由于电网阻抗的存在,系统中PCC处扰动电压也会存在两个相应频率分量:

(8)

系统中PCC处扰动电压与并网扰动电流之间的关系用相量表示为:

(9)

(10)

式(9)和式(10)分别表示了ωp和2ω0-ωp频率下PCC处扰动电压和并网扰动电流之间的关系。

另结合1.1节中得到的表征逆变器单频率输入、双频率输出特性的两个解析表达式,可以得到如下相量等式:

(11)

(12)

由式(9)、式(10)、式(11)、式(12)可得到能表征三相并网逆变器系统小信号特性的相量框图如图2所示。

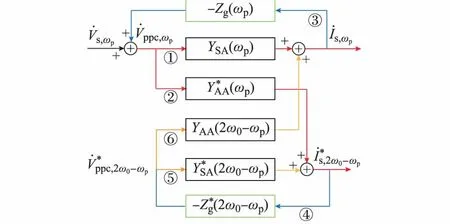
图2 三相并网逆变器系统小信号模型相量框图Fig.2 Phasor block diagram of small signal model for three-phase grid-connected inverter system

图2中各路径含义说明如下:支路①表示PCC处ωp频率的电压作用于逆变器产生ωp频率的并网电流;支路②表示PCC处ωp频率的电压作用于逆变器产生2ω0-ωp频率的并网电流;支路③表示ωp频率的并网电流流经电网阻抗产生ωp频率的PCC电压;支路④表示2ω0-ωp频率的并网电流流经电网阻抗产生2ω0-ωp频率的PCC电压;支路⑤表示PCC处2ω0-ωp频率的电压作用于逆变器产生2ω0-ωp频率的并网电流;支路⑥表示PCC处2ω0-ωp频率的电压作用于逆变器产生ωp频率的并网电流。

在图2中,用共轭相量表示系统中2ω0-ωp频率下的扰动分量。由该框图分析可知:对并网逆变器系统中PCC电压施加一个ωp频率下的扰动,由于逆变器中锁相环dq轴结构的不对称会使得系统中存在ωp和2ω0-ωp频率的并网扰动电流(如图中红色箭头标识路径所示);而电网阻抗Zg的存在,使得PCC处存在与并网扰动电流相对应的两个频率下的扰动电压(如图中蓝色箭头标识路径所示);这两个频率下的PCC处扰动电压又会各自产生两个对应频率下的并网扰动电流(如图中红色和橙色标识路径所示)。

上述分析表明并网逆变器系统中两个扰动频率分量相互耦合的机理在于:①dq轴不对称环节(锁相环)导致逆变器表现出单频率扰动电压输入、双频率扰动电流输出特性,使得系统中会同时存在两个扰动频率分量;②电网阻抗的存在导致两个频率的扰动电流产生相应的PCC扰动电压,从而进一步作用于逆变器,使得两个频率分量相互耦合。

2 并网逆变器等效导纳的建立及稳定性判定

在明确了并网逆变器系统中两个扰动频率相互耦合机理的基础上,本节建立逆变器在ωp扰动频率和2ω0-ωp扰动频率下的等效导纳,进而分析了并网逆变器系统在这两个频率下的稳定特性。最终,得到了可以判定整个并网逆变器系统稳定性的方法。

2.1 ωp频率下逆变器等效导纳的建立及稳定特性分析

利用图2所示框图可推导得到并网逆变器系统在ωp频率下的并网电流满足:

(13)

上式中Yinv(ωp)表示ωp频率下逆变器的等效导纳,其表达式如下:

Yinv(ωp)=YSA(ωp)-

(14)

由式(13)可以得到并网逆变器系统在ωp频率下的等效电路如附录A图A1所示。根据系统等效电路,由阻抗判据[20]可知,采用奈奎斯特判据判定Yinv(ωp)Zg(ωp)项的稳定性即可分析出并网逆变器系统在ωp频率下的稳定特性。

2.2 2ω0-ωp频率下逆变器等效导纳的建立及稳定特性分析

对于系统中2ω0-ωp频率下的分量,同样利用图2所示的相量框图,可以得到:

(15)

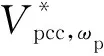
(16)

式(15)中YSA(2ω0-ωp)表示并网逆变器系统中2ω0-ωp频率下的逆变器等效导纳,具体表达形式如式(4)所示。根据式(15)得到并网逆变器系统在2ω0-ωp频率下的等效电路如附录A图A2所示。类似的,由阻抗判据[20]可知,采用奈奎斯特判据判定YSA(2ω0-ωp)Zg(2ω0-ωp)项的稳定性即可分析出并网逆变器系统在2ω0-ωp频率下的稳定特性。

由上述2.1节和2.2节分析结果可以得到针对整个并网逆变器系统的稳定性判定方法:Yinv(ωp)Zg(ωp)和YSA(2ω0-ωp)Zg(2ω0-ωp)项对应的奈奎斯特曲线在复平面内都不包围(-1,j0)点,则并网逆变器系统稳定;否则,系统不稳定。该稳定性判定方法物理意义清晰,且相比采用广义奈奎斯特判据的方法,稳定性判定过程更简单,能给出系统稳定裕量,指导逆变器控制器设计。

3 并网逆变器等效导纳验证

上述2.1节和2.2节得到了并网逆变器在ωp频率和2ω0-ωp频率下的等效导纳Yinv(ωp)和YSA(2ω0-ωp),本节采用仿真验证这两个导纳模型的正确性。

3.1 ωp频率下逆变器等效导纳验证

为了验证并网逆变器系统在ωp频率下的逆变器等效导纳模型Yinv(ωp)的正确性,在MATLAB/Simulink中搭建了如图1所示的并网逆变器仿真模型。模型中逆变器的相关参数如下:Vdc=400 V,idr=6 A,iqr=0 A,L=1.5 mH,kp=3.54,ki=1 411,kpp=8.58,kpi=5 706,RL=0.15 Ω,f0=50 Hz,开关周期Ts=10-4s,τf=0.136 ms。

另外,并网逆变器系统仿真模型中电网侧的等效拓扑和部分参数见附录A图A3,图中电网电感值Lg设为2 mH,求出图中电网等效阻抗表达式为:

(17)

对仿真模型中的三相电网电压vga,vgb,vgc注入ωp频率下的三相对称扰动。采集系统中PCC电压和并网电流进行快速傅里叶变换(FFT)分析,取电流和电压中的ωp频率分量进行运算得到逆变器的等效导纳Yinv(ωp)。改变注入扰动电压频率,重复以上步骤,可以得到各个频率下系统的阻抗点。

附录A图A4中浅绿色曲线为根据式(14)所示的并网逆变器系统中ωp频率下逆变器等效导纳解析模型绘制出的幅频和相频曲线,红色的点为仿真测量计算得到的数据点。图中仿真测量结果和解析模型吻合得较好,即仿真验证了解析模型Yinv(ωp)的正确性。

3.2 2ω0-ωp频率下逆变器等效导纳验证

前述2.2节分析出并网逆变器系统在2ω0-ωp频率下的逆变器等效导纳模型为YSA(2ω0-ωp)。为了验证该模型的正确性,在上述3.1节搭建的MATLAB/Simulink模型基础上,将电网阻抗设置为0。

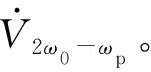
类似的,附录A图A5中绿色曲线是根据解析模型YSA(2ω0-ωp)绘制出的幅频、相频曲线。图中仿真测量计算得到的红色数据点和解析模型曲线吻合得较好,即仿真验证了2ω0-ωp频率下逆变器等效导纳模型YSA(2ω0-ωp)的正确性。

4 并网逆变器稳定性判定结果验证

为了验证本文并网逆变器系统稳定性判定结果的正确性,实验室搭建了三相并网逆变器平台。实验平台的拓扑结构和相关参数分别见图1和3.1节。电网拓扑结构和部分参数见附录A图A3,电网电感值Lg可变。

4.1 电网电感值变化时系统稳定性分析验证

当电网电感值Lg为2 mH时,在复平面中画出Yinv(ωp)Zg(ωp)和YSA(2ω0-ωp)Zg(2ω0-ωp)项对应的奈奎斯特曲线,如附录A图A6所示。图中蓝色实线代表Yinv(ωp)Zg(ωp)项对应的奈奎斯特曲线,粉红色虚线代表YSA(2ω0-ωp)Zg(2ω0-ωp)项对应的奈奎斯特曲线。从图中可以看出，两条奈奎斯特曲线都不包围(-1,j0)点,由此可以判定出并网逆变器系统稳定,并且可以得到系统的稳定相角裕量为22°。

利用文献[14,18]中的方法,画出相应的广义奈奎斯特曲线,分别如附录A图A7和图A8所示。从两图中均可判定出并网逆变器系统稳定。实验测量得到的PCC电压和三相并网电流波形如图3所示,图中并网电流呈标准的正弦波。相应的PCC电压和并网电流FFT分析结果分别如附录A图A9和图A10所示,图中结果显示PCC电压和并网电流中除50 Hz基频分量外无其他明显谐波分量。因而实验结果表明系统是稳定的,验证了稳定性判定结果的正确性。

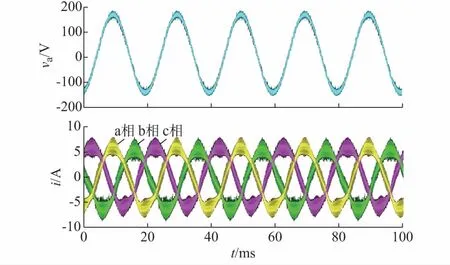
图3 Lg=2 mH时PCC电压和三相并网电流Fig.3 Waveforms of PCC voltage and three-phase grid-connected current for Lg=2 mH

当电网电感值为3 mH时,画出Yinv(ωp)·Zg(ωp)和YSA(2ω0-ωp)Zg(2ω0-ωp)项对应的奈奎斯特曲线如附录A图A11所示。从图中可以判定出并网逆变器系统稳定,并且系统稳定相角裕量为8°。另外,利用文献[14,18]中的方法,画出相应的广义奈奎斯特曲线分别如附录A图A12和图A13所示，从两图中也可以判定出系统稳定。实验测量结果如附录A图A14所示,图中并网电流无明显畸变,说明系统稳定,验证了稳定性判定结果的正确性。

当电网电感值Lg增加至3.5 mH时,同样在复平面中画出Yinv(ωp)Zg(ωp)和YSA(2ω0-ωp)·Zg(2ω0-ωp)项对应的奈奎斯特曲线,如附录A图A15所示。从图中可以看出Yinv(ωp)Zg(ωp)项对应的奈奎斯特曲线包围了(-1,j0)点,由此可以判定出并网逆变器系统不稳定。

在电网电感值Lg=3.5 mH的条件下,同样利用文献[14,18]中的方法,画出相应的广义奈奎斯特曲线,如附录A图A16和图A17所示，从两图中均可以判定出并网逆变器系统不稳定。实验测量得到的PCC电压和三相并网电流波形如图4所示,从图中可以看出并网电流波形已经发生了严重的畸变。这种情况下,相应的PCC电压和并网电流FFT分析结果分别如附录A图A18和图A19所示。图A19显示,并网电流中除基频分量外,317 Hz和217 Hz频率处的谐波幅值明显比较大,表明系统存在频率耦合效应。因此,实验结果表明系统是不稳定的,即实验验证了稳定性判定结果的正确性。

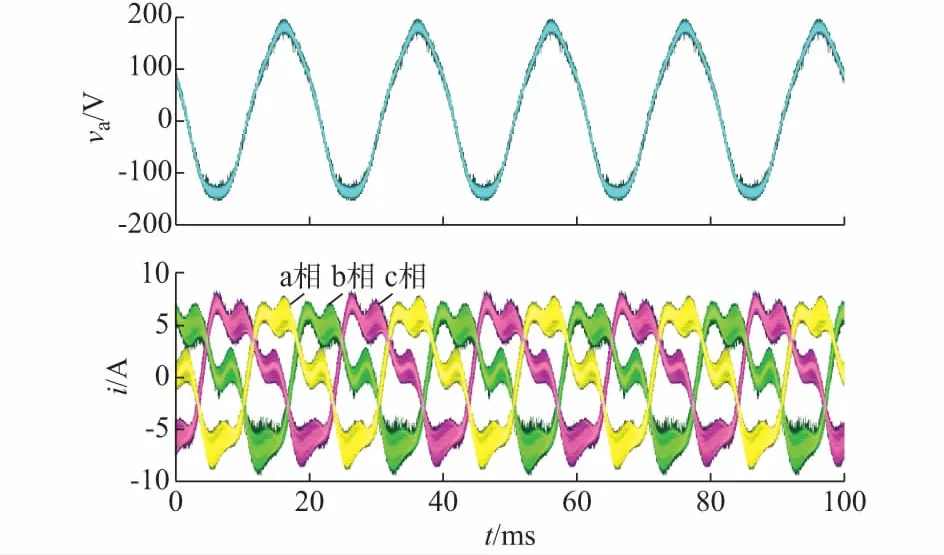
图4 Lg=3.5 mH时PCC电压和三相并网电流Fig.4 Waveforms of PCC voltage and three-phase grid-connected current for Lg=3.5 mH

上述3种条件下,本文稳定性判定结果均与现有文献[14,18]的判定结果一致,说明考虑频率耦合因素,本文采用奈奎斯特判据也能准确地判定出系统的稳定性,实验也进一步验证了本文稳定性判定结果的正确性。相比文献[14,18]中采用广义奈奎斯特判据的两类方法,本文提出的稳定性判定方法判稳过程简单,且能给出系统稳定裕量。

4.2 电流控制器dq轴参数不对称变化时系统稳定性分析验证

前述1.2节中指出dq轴不对称环节和电网阻抗的存在导致系统存在频率耦合效应,这一耦合效应会影响系统的稳定性。因此,本节对电流控制器dq轴参数不对称的影响进行了分析验证。

当三相并网逆变器参数如3.1节所示,即电流控制器dq轴参数对称一致,且电网电感为3.5 mH时,上述4.1节理论分析、实验结果表明系统是不稳定的。本节变化控制器q轴参数,令控制器d轴参数kpd=3.54,kid=1 411,控制器q轴参数kpq=5.31,kiq=2 116.5,即控制器dq轴参数不对称,进而分析系统的稳定性。

类似地,在复平面中画出系统的奈奎斯特曲线,如附录A图A20所示。从图中可以看出两条奈奎斯特曲线都不包围(-1,j0)点,由此判定出系统是稳定的,并且系统稳定相角裕量为10.5°。相应的实验结果如图5所示,从图中可以看出三相并网电流无明显畸变,即系统是稳定的。

图5 电流控制器dq轴参数不对称时PCC电压和三相并网电流Fig.5 Waveforms of PCC voltage and three-phase grid-connected currents for asymmetric dq axis parameters of current controller

上述4.1节中控制器dq轴参数对称时系统不稳定,本节变化q轴参数,即控制器dq轴参数不对称时系统稳定,证明系统电流控制器dq轴参数对称与否会影响系统的稳定性。针对这一影响因素的详细分析讨论将在后续工作中进行深入研究。