计及风电时间相关性的鲁棒机组组合
2018-09-27范刘洋汪可友李国杰葛维春
范刘洋, 汪可友, 李国杰, 吴 巍, 葛维春
(1. 电力传输与功率变换控制教育部重点实验室(上海交通大学), 上海市 200240;2. 国网辽宁省电力有限公司, 辽宁省沈阳市 110006)
0 引言
近年来,随着技术的成熟和成本的降低,风电、太阳能等可再生能源装机容量得到了快速的提高[1]。国家风电发展“十二五”规划中提出,2020年中国风电装机规模将达到2×108kW,风电装机容量将占总装机容量的11%[2]。风电具有间歇性、波动性等特点,日前预测误差可达在20%,远高于负荷预测误差[3]。大规模风电的接入,给电力系统调度带来了巨大挑战。
近年来,鲁棒优化理论被应用于这一领域,并取得良好效果[4-9]。鲁棒优化使用闭凸集合描述参数的不确定性,并计算目标函数在“最坏情况”下的最优问题[10-13]。相比于随机规划,鲁棒优化不要求获得随机变量分布函数,不需要生成典型场景,更易于实施。但另一方面,鲁棒优化结果一般保守性较强。
鲁棒优化结果的保守性直接受到不确定参数集合的影响。最早,文献[10]采用每个不确定变量在一定置信水平下的上下界作为不确定集。近年来,文献[11-12]采用椭球集合描述不确定集,文献[4-5,7]采用盒式集合描述不确定集,进一步降低了鲁棒优化的保守性,由于盒式集合的线性性质,这种不确定集合在电力系统中应用更为广泛。
但是,以上不确定集合均假定每个时刻不确定参数服从的是独立分布律,这并不符合实际情况。以含风电的调度问题为例,当风电场之间距离较近时,两个或多个风电场之间的出力会具有相关性。这种现象已经在风电场建设规划、风险机组组合、随机规划场景生成等问题中被注意到[14-17]。
然而对风电预测误差时间相关性(以下简称“时间相关性”)的研究仍然较少。电力系统在制定机组组合计划时,需要的是提前一天到一周内的风速预测信息。这一时间尺度的风速预测往往使用数值天气预报(numeric weather predictor,NWP)模型[18]。该方法根据风场周围的气压、气温、等高线以及障碍物等物理信息构建风速的微分方程表达式,对风速进行预测。文献[18-19]根据大量的风电场运行历史数据,建立了1 h步长的一阶风速马尔可夫链模型。其中,状态转移概率矩阵呈近似对角分布,对角线及其附近元素数值较大,这从侧面验证了风速在时间上的相关特点。文献[20]分析了爱尔兰风电场的风电数据,直接指出风电预测误差序列具有明确的自相关性特性,并提出利用该特性降低风电预测误差的统计方法。文献[21]将风电预测误差的协方差矩阵加入高斯分布中,并验证考虑相关性的模型可以提高鲁棒最优潮流模型的经济性。在鲁棒机组组合(RUC)问题中,理论上同样可以利用时间相关性特点,剔除一些概率密度较低的场景,降低不确定集合的保守性。但是鲁棒优化本质为多层优化问题,对约束条件要求较高,统计方法的分析结果需要表示为线性约束才能应用于鲁棒优化算法中。
本文首先以德国巴登—符腾堡州风电接入真实数据为基础,验证了时间相关性的存在,并以Pearson相关系数(PCC)为相关性测度,提出了不确定变量的相关性约束。接着,根据利用不确定集合的离散型特点,将相关性约束近似简化为线性约束。本文将简化后的相关性约束加入RUC中,并在列与限制生成(C&CG)算法的基础上改进Bender’s分解后子问题的求解方法,用于求解含有相关性约束的RUC。最后在真实风电预测数据的基础上,大量仿真实验验证了所提相关性约束的有效性。
1 风电预测误差的时间相关性模型
1.1 时间相关性验证
在进行风电预测误差的时间相关性建模之前,首先需要确认其存在性。对于某一个时间序列x(t),自相关系数用于表征序列本身在不同时间的相关程序,该数值越高,表示历史数据对当前时刻的影响程度越大。自相关系数计算公式为:
(1)
t时刻的相对预测误差et可以表示为:
(2)

记相对误差序列为:
s0=[e1e2…eN-1]
(3)
s1=[e2e3…eN]
(4)
式中:N为风电预测的样本数量。显然,s1是s0向后平移一个时间间隔的序列。
以德国巴登—符腾堡州的风电接入数据为预测误差序列样本[22]。图1是以2015年1月样本数据序列生成s0和s1向量所绘制的散点图。图中:下标i=1,2,…,N-1;j=2,3,…,N。从图1中可以直观地看到,s0和s1向量具有明显的正相关性。为了进一步确认相关性水平,计算s0和s1的PCC。相关系数越大,则说明历史数据对当前数据的影响越强,预测误差的时间相关性越高。若相关系数大于0.6,则认为预测误差具有显著的时间相关性。考虑到该地区气候的季节特性,对风电预测数据以月为单位进行检验。预测数据的时间间隔为1 h。

图1 预测误差序列散点图Fig.1 Scatter plot of predictive error sequence
图2是对2015年每个月内的预测数据进行相关性计算的结果。可以看到,各个月份都体现出了正相关性,平均相关系数在0.69左右,表明之前的预测误差具有时间相关性假设是成立的。

图2 以1 h为间隔的预测误差样本Pearson相关性系数Fig.2 Pearson correlation coefficient of 1 hour interval predictive error sequence
1.2 时间相关性约束建模
在确认时间相关性后,可以利用这一点,进一步缩小不确定集合规模,将相关性较低的预测误差序列剔除,降低鲁棒优化的保守程度。

图3 某月内每天预测误差相关系数分布Fig.3 Distribution of daily correlation coefficient for predictive error within a month
图3是某典型月内,每天的预测误差相关系数分布直方图。其中的红色曲线是对预测误差分布进行Kernel拟合的曲线。可以看到,由于样本数量较少,预测误差分布规律不明显,并非典型的正态分布。但是可以确定的是,置信水平为95%时,样本的相关系数均在[0.36,1]范围内。基于以上分析,可以对不确定集合加入时间相关性约束。
(5)
式中:pe为风电出力的日前预测场景;p为风电出力的可能场景;C(·)为PCC计算函数;γ为可能场景与预测场景的时间相关性下限,与预设的置信水平有关;ρ为置信水平。
式(5)本质上是预测误差时间序列自相关性的体现。由于相关性约束的存在,独立分布的时间序列(比如白噪声)将不被优化模型考虑,因此鲁棒优化可以得到更加经济的结果。γ可以作为鲁棒优化保守程度的调节参数,置信水平越高,γ越小,不确定集合越大,优化结果越保守。
1.3 时间相关性约束简化
式(5)是从时间相关性角度建立的约束条件。但是相关系数计算函数C(·)计算过程复杂,是一个高度非线性的函数。式(5)难以直接加入鲁棒优化中,必须进行简化处理。
盒式不确定集合一般形式可以表示为:
(6)
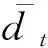
Δ不等于0时,式(6)描述的不确定集合是一个多维空间中的多面体。文献[4]指出,鲁棒优化过程中,最差情景时不确定变量d取值必定为该多面体的某个极点。进一步地,文献[23]指出,当Δ为整数时,对于鲁棒优化问题,式(6)描述的集合可以改写为以下形式:
(7)

容易理解,在式(7)表示方式下,原本连续的预测误差序列e=d+-d-。所以式(5)中对从e中截取而生成的s0和s1的相关系数的约束,可以转化成对d+和d-的约束。考虑到d+和d-的在式(7)完全对称,下文的讨论将以d+为例。

(8)
(9)
记d+序列之和为Δ+,这里定义的Δ+可以类比式(6)中的不确定预算Δ。并定义变化标志变量v+为:
(10)
相应的,记v+求和为Λ+,类比Δ+,称Λ+为该序列的 “变化量预算”。因为Λ+代表着原序列出现前后不一致的次数,并给出以下定理。
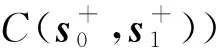
证明1PCC的计算公式如下:
(11)
式中:cov(·)为求协方差函数。
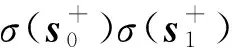
(12)
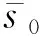

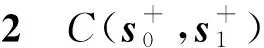
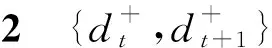
(13)
这4种组合中,出现{0,1}和{1,0}次数之和为Λ+。出现{1,1}的次数为(2Δ+-Λ+)/2。出现{0,0}的次数为N-1-(2Δ+-Λ+)/2-Λ+。
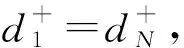
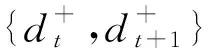
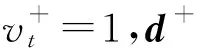
定理2是式(5)化简的重要依据。预测误差在使用连续集合式(6)描述时,本身具有无穷多种可能场景。即使使用离散集合式(7)进行描述,也存在多达2N种可能。由定理2可知,并不需要对如此多种可能场景的相关系数一一计算。所有Λ+和Δ+相同序列的相关系数都相同。为了更形象地解释定理2,利用表1进行说明。

表1 典型序列的PCC与不确定预算、变化量预算的关系Table 1 Relationship between PCC and uncertainty budget/variation budget in typical sequences
表1展示了6组典型序列的相关系数与不确定预算、变化量预算的关系。比较前三组和后三组序列可以看到,在变化量预算Λ+一定的情况下,即使序列具体排列不同,相关系数也不会变化。这样一来,仅需要研究Λ+,Δ+和相关系数的关系即可。对相系数的约束可以转化为对Λ+和Δ+参数的线性约束。
至此,考虑风电相关性的不确定集合可表示为:
(14)
式中:Λ为总的不确定预算,即d+和d-序列的不确定预算Λ+与Λ-之和;上标u表示启动,d表示关停。
对于某个风电场在N个时间间隔内出力的不确定集合,式(7)需要2N个整数变量,而式(14)需要6N个整数变量,故而考虑时间相关性约束后,鲁棒优化的求解时间可能增加。
2 计及时间相关性的鲁棒优化求解
在第1节中,通过对相关系数的简化,将非线性的相关性约束式(5)简化为线性约束,并用式(14)表示改进后的不确定集合。本节将讨论含有式(14)的鲁棒优化求解算法。
在电力系统中,RUC的一般形式为(考虑到篇幅限制,这里只列出简洁模型,详细模型见附录A):
(15)
s.t.Fx≤f
(16)
Ax+By≤g
(17)
Iyy+Idd=k
(18)
My+Nd≤l
(19)
式中:x为机组状态变量,是二进制离散变量;y为机组参数变量,是连续型变量;其余变量含义见文献[4]。式(16)表示机组对机组状态的约束,包括启停逻辑约束、最小启停时间约束、备用率约束等;式(17)表示机组状态和机组出力关系约束,包括容量约束,爬坡率约束等;式(18)表示系统的功率平衡约束;式(19)表示传输线安全约束。
本文文献[13]提出的C&CG算法进行求解。由于式(14)为离散型集合,本文中对Bender’s分解后产生的子问题的求解不再采用文献[13]的方式。Bender’s分解后子问题为:
(20)
写出min问题部分对偶形式,式(20)变为双线性规划问题:
(21)
s.t.b+λTB+ηTIy+θTM=0
(22)

(23)
式中:λ,η,θ分别为式(17)至式(19)的拉格朗日乘子。
显然,对双线性项(ηTIdd,θTNd)的处理是求解的关键。将式(14)同样写为简洁形式:
{d|d=Tz+T0,Rz≤r}
(24)
式中:z为包括v,d+,d-的二进制变量。则双线性项变为ηTCz,θTGz,其中C=IdT,G=NT。以ηTCd为例:
(25)
显然,只有cij不为0时,对式(25)的计算才是有意义的。考虑到zj的二进制性质,引入附加变量qk:
-zjQ≤qk≤zjQ
(26)
ηi-(1-zj)Q≤qk≤ηi+(1-zj)Q
(27)
其中,q的下标k与i,j的关系为:矩阵C中第k个不为零的元素为cij。Q为q的上界。容易理解,式(26)和式(27)等价于当zj等于0时,qk等于0;当zj不等于0时,qk等于ηi。因此,qk=ηizj。
至此,子问题由双线性规划转化为混合整数线性规划,可以被CPLEX等成熟的商业求解器求解。但是,注意到该问题的求解效率与矩阵C和矩阵G的稀疏性密切相关。矩阵C由功率平衡约束转化而来,规模较小;而矩阵G由传输线安全约束转化而来,规模较大。在实际计算时,可以先忽略传输线安全约束,待计算完成后,再校验各条线路上功率是否越限。如越限,则将该线路加入传输线安全约束中,再次计算。
3 算例分析
3.1 参数说明
为了验证本文提出的考虑时间相关性的不确定集合的有效性,对以下三种机组组合模型进行对比。
1)传统机组组合(TUC)。采用确定性优化算法,不考虑风电预测误差。
2)RUC。采用第3节所述的鲁棒优化算法,考虑风电预测误差,但不考虑时间相关性,对不确定集的描述如式(7)所示。
3)计及时间相关性的鲁棒机组组合(TRUC)。采用第3节所述的鲁棒优化算法,对不确定集的描述如式(14)所示。
电力系统模型采用IEEE 118节点标准算例,包括118条母线、54台发电机以及186条传输线[24]。风电接入和系统负荷数据来自德国巴登—符腾堡州电网运营商Transnet BW的公开数据[22]。对风电及负荷数据稍作调整,使其符合IEEE 118节点电力系统正常运行的功率范围。调整后系统最大负荷大约为6 500 MW,最大风电渗透率大约为40%,平均风电渗透率大约为8%。以该地区2015年运行数据为历史数据,对不确定集合参数进行估计。
三种机组组合算法在MATLAB 2014b及YALMIP上完成[25]。混合整数规划采用CPLEX 12.6进行求解。鲁棒优化结果的间隙误差(即上下界之差除以下界)上限为0.1%。所有计算在配备处理器型号为Intel Core i7-4790 4核3.6 GHz以及16 GB RAM的个人计算机上完成。
3.2 典型日优化结果比较
为了验证本文提出的TRUC的有效性,首先以某典型日风电预测情况为输入数据,计算三种机组组合模型的求解结果,并对机组组合结果进行安全校验。安全校验指的是在风电场真实出力情况下,日前制定的机组组合计划是否能够满足电力系统安全性要求[5-7]。其数学模型为:
(28)
式中:s1至s4为保证式(17)和式(19)满足而引入的松弛变量。
若R(x)=0则说明在s1至s4均为零的情况下,系统功率平衡约束、传输线安全约束等可以满足。反之,R(x)>0则代表机组组合无法满足系统安全性要求,此时需要实施切负荷或弃风等紧急措施。在Δ等于8,Λ等于2时,三种模型求解结果如表2及图4所示。

表2 三种模型典型日优化结果对比(Δ=8,Λ=2)Table 2 Comparison of optimization results of three models in a typical day (Δ=8, Λ=2)
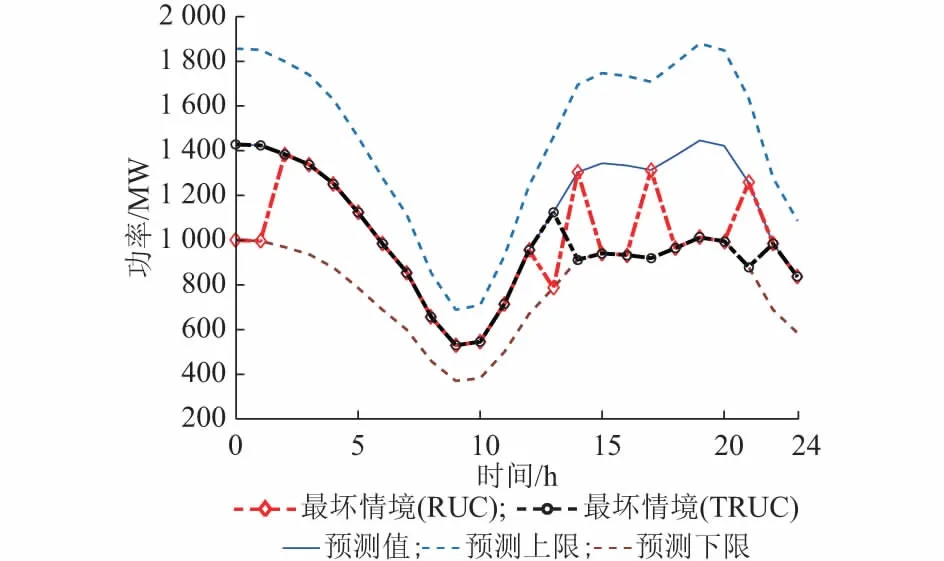
图4 典型日风电预测及“最坏情况”求解结果曲线图(Δ=8,Λ=2)Fig.4 Wind power prediction and calculation results of “the worst case scenario” in a typical day (Δ=8, Λ=2)
该算例的优化结果显示,相比于RUC算法,TRUC算法在保证安全性的基础上,提高了机组组合经济性,降低了鲁棒优化的保守程度。为进一步解释TRUC机理,将RUC与TRUC计算出的“最坏情境”在图4中标出。
RUC算法得到的“最坏情境”如图4中红线标注,其中出现多次风电爬坡事件,风电出力在预测值及最小值之间多次跳动。根据前文分析,该情境出现概率较低。而TRUC算法中,在相同的不确定预算时,由于变化量预算的存在,限制了预测误差变化次数,剔除了概率较低的情境,提高了优化经济性。
TRUC优化结果受到两个参数的影响,不确定预算Δ和变化量预算Λ。下面比较不同的Δ和Λ取值对优化结果的影响,如图5所示。

图5 不同Δ和Λ情况下的求解结果Fig.5 Optimization results under different Δ and Λ
从图5中可以看到,对优化结果影响最大的是不确定预算的值。比较Δ等于6,8,10的三条曲线,优化结果大约变化了2%。而变化量预算对优化结果的影响要相对小一些。以Δ曲线为例,比较Λ等于1和Λ等于6,成本变化了大约0.4%。并且,在Λ大于4时,成本变化并不明显。由此,可以将Λ看作一个辅助参数,是在决策者对Δ进行估计后,对调度保守性的更精细的调节手段。
3.3 长期优化结果比较
3.2节中,已经看到变化量预算对优化结果的调节作用。但是担心加入变化量预算的约束,是否会对系统的安全性造成影响。从图5中可以看到,这种可能性是存在的。因此,对一段较长时间内TRUC算法的安全性进行评估。以德国巴登—符腾堡州2016年1月到7月间风电接入为输入数据,计算三种算法的日前机组组合结果,并进行安全评估。
Δ的取值一般由决策者估计,Δ对优化结果的影响已经在多篇文章中有讨论[4-7]。这里固定Δ取值为8,改变Λ的取值,来考察Λ对优化结果及安全性的影响。
表3是三种机组组合模型计算结果的对比。其中,通过安全校验比例代表了不出现切负荷或弃风等措施的可能性,该数值越大,代表算法的可靠性越高。从表3中可以看到,相比于RUC算法,TRUC算法提高了机组组合的经济性。在Λ=2时,TRUC可靠性与RUC接近,机组组合成本降低了48万美元。在Λ=3时,可靠性与RUC相同,但成本降低了约8万美元。
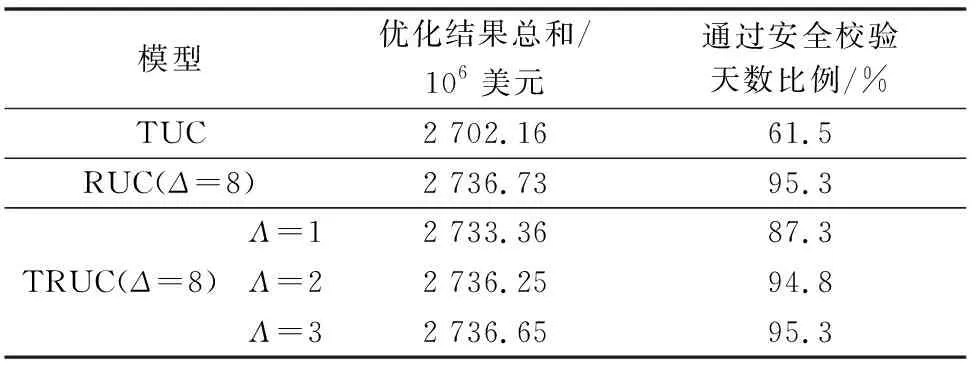
表3 三种模型长期优化结果对比Table 3 Comparison of optimization results of three models in a long term
4 结语
本文研究了风电预测误差的时间相关性特点,并提出了TRUC算法。该算法中在“不确定预算”外,加入了“变化量预算”参数,作为鲁棒优化保守性的另一个控制参数。由本文的理论研究及仿真实验得出如下结论。
1)某些预测方法得到的风电预测误差存在强烈的时间相关性。利用时间相关特点,可以进一步缩小不确定集合范围,降低鲁棒优化保守性。
2)利用不确定集合离散型特点,预测误差序列的自相关系数计算公式可以得到简化。相关性约束可以近似简化为线性形式。
3)在真实风电数据进行的仿真实验上,验证了该算法能够在不降低机组组合鲁棒性的前提下,提高调度计划的经济性。
在含风电的RUC问题中,如何将“弃风”加入模型研究中,通过鲁棒优化手段,进一步降低“弃风”比例,是本文下一步研究的方向。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
