基于梯度提升的城市轨道交通客流量预测分析

丁 聪 倪少权 吕红霞

(1.西南交通大学信息科学与技术学院，611756，成都；2.西南交通大学交通运输与物流学院，610031，成都//第一作者，硕士研究生)

客流量的预测和分析是城市轨道交通规划和建设的重要依据。城市轨道交通客流与群众出行规律密切相关，通常具有较强的时间序列特征。过去已有相关领域的研究人员基于ARIMA模型实现了客流量的预测，通过对模型进行各方面优化，提升了预测效果[1-2]。近年来机器学习技术得到广泛应用，有的采用特殊结构神经网络[3-4]、支持向量机[5]等方法实现客流量预测，并通过分析客流特征研究居民出行规律和交通规律。本文在参考已有算法的基础上[6-8]，使用梯度提升决策树混合模型预测城市轨道交通客流量，并分析相关影响因素特征。

1 梯度提升决策树基本原理

梯度提升决策树是一种通过构建多个弱学习器、并将之组合形成强学习器的集成模型。通常使用分类回归决策树作为弱学习器。分类回归决策树是一种应用较为广泛的决策树实现方法，其每一次训练尽可能遍历所有可能的属性取值，依据最佳分割点将样本数据分为2个部分，以递归分割的方式，不断循环直至终止条件。

梯度提升属于提升算法体系的一种，由斯坦福教授J.H.Friedman提出[6-7]。其基本思想是利用损失函数的负梯度在当前模型下的值作为模型本次训练结果残差的近似，并以该值作为下一次训练的目标。模型的输出结果将向着损失函数减小的方向移动。以分类回归树为弱学习器的梯度提升法的基本原理可表示如下：

对于样本空间N={(x1,y1),(x2,y2),…,(xN,yN)}，目标是找到1个预测函数F(x)，使得在所有x到y的映射下的损失函数L(y,F(x))最小。预测函数表示为：

(1)

式中：

h(x;am)——弱学习器的第m棵子树，m=1,2,…,m;

am——第m棵子树的参数；

βm——该子树的权重。

若第m次训练生成的预测函数为Fm(x)，则优化问题等价于找到新子树的参数(βm.am)，使：

(2)

针对上述条件，整个梯度提升模型的更新流程为：

第1步，初始化第1棵回归树：

(3)

第2步，对于m=1，2，3，…，M，损失函数的负梯度为：

(4)

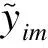
(5)

(6)

更新预测函数：

Fm(x)=Fm-1(x)+νβmh(x;am)

(7)

式中：

ν——控制学习速率的步长。

ν越小，则需要更多的训练次数才能达到要求的预测精度;而ν设置得过大，则可能无法达到较高的预测精度。

梯度提升法中可使用最小二乘回归为损失函数。此时，损失函数的负梯度就是预测值与真实值之间的残差，其表示形式为：

(8)

随机森林的核心思想是仅选取部分样本及部分特征训练子树，训练速度更快，其子模型之间相互独立，不容易出现过拟合问题。由于每次训练是随机的，子树之间缺少关联性，预测结果不会固定朝着某一方向移动，虽然最终预测的方差能随着子树数量的增加而降低，但偏差难以降低。梯度提升法每次训练都依赖于前一次模型的预测结果，预测结果的方差和偏差均能随训练次数的增加而下降。但是，该算法属于中心化算法，不易并行计算，故训练速度较慢。

为解决随机森林与梯度提升法存在的问题，构建随机森林和梯度提升的混合模型，使用随机采样后的属性特征和样本子集作为训练样本，并在上层使用梯度提升法。这样既能较好地解决训练速度问题，也能较好地提升预测效果。

2 客流预测模型机理及数据集特征处理

2.1 模型预测机理

地铁日均客流量具有明显的周期性和季度性。其时序性决定了日客流量与日期、历史客流量直接相关。天气、气温及节假日等则是引起客流量波动的重要因素。使用树模型的实质，即通过样本数据探究以上相关因素的差异性对流量大小的影响。

根据树模型的原理，在理想状态下，对于任意1组特征组合，都应存在1个客流量集合与之对应，同1集合内客流量的均值将作为符合该特征组合的客流量预测值。模型每一次迭代都将根据以上特征对样本进行若干次划分，特征与预测目标较高的相关性保证了分类效果。根据梯度提升算法，模型第一次训练以实际客流进行拟合，此后以上一次预测结果与实际值的残差来训练子树，从而逐步缩小预测残差，降低拟合偏差。

数据样本及其特征的选择将极大影响模型的预测结果，只有合理的样本特征才能实现模型的最大作用。因此，需选定样本的输入与输出，并对样本数据进行特征工程处理，以保证样本属性与特征的有效性。

2.2 数据集特征处理

根据预测机理及相关研究，在分析影响城市轨道交通日客流量的若干因素后，搜集相关数据进行特征处理形成合适的训练样本。本试验采用的数据来源为北京地铁2015年1月1日至2017年7月17日15条运营线路的日客运量及对应时间的相关特征数据，共929个样本。特征数据包含离散值和连续值。离散值应按等级分类、合并或进行one-hot编码。为保证决策树分类效果，应根据特征与客流间的相关性作为评价标准，应将不相关数据或具有较多噪音数据进行剔除、替换和合并处理，以实现降维，最终形成适用于模型的数据集。

根据以上分析对相关属性特征进行处理，得到训练特征。工作日与周末使用同一个状态进行分类；天气数据按照类别进行合并处理，分为7个等级；节假日对客流量有较大的影响，春节、国庆与其他节假日的差异性通过4个类别划分。通过Python模块Seaborn和Pandas可进行编程，以实现数据图表的可视化输出，图1以热图形式展示了预处理后数据集各向量间的皮尔逊相关系数。

图1 皮尔逊相关系数热图

由图1可见：地铁的日客流量与年、月具有一定的相关性；结合人口统计分析，北京地区常住人口居住人口具有缓慢增长趋势，客流量也随之增长；日平均温度的相关系数达到0.19，反映了地铁客流一定的季节性，但相关性较弱；高度相关的属性特征包括星期、周末，表现了客流量的时序性和周期性；节假日是客流量波动的重要原因；日客流量与前一周历史客流量也具有相关性，故历史客流可考虑选作为训练特征，但是如直接使用这些数据，则可能因信息量重合而造成过拟合等问题。将前一周的历史客流量均值作为修正后的训练特征值代替同期客流量，并参与模型训练，以对预测进行修正，即

(9)

最终使用的样本数据及存储形式说明如表1所示。

表1 数据集说明

3 试验与仿真

使用Python机器学习模块Scikit-learn[9]实现模型的建模与仿真。取前850个样本作为训练集，后79个样本作为测试集，模型输出为对应测试集下的日客流量。对模型参数进行多次调整，每种参数组合进行2 000次训练。令T为样本的特征总数，选取部分参数组合下的预测结果如表2所示。由表2可知，回归子树的深度N与训练子集使用的特征数t越大，训练时间越长。

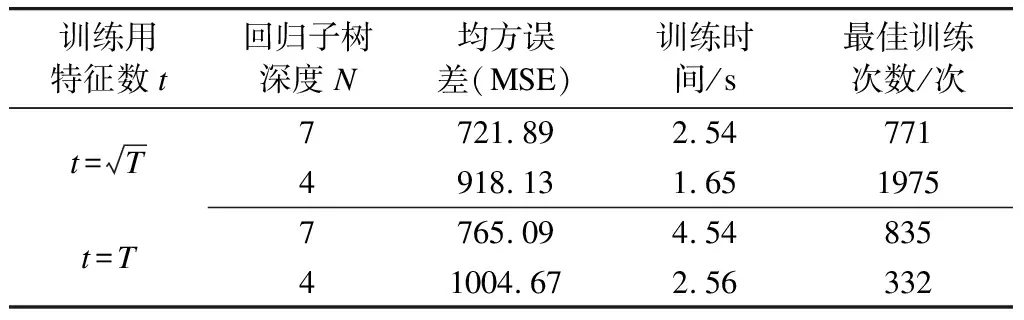
表2 各参数下模型训练结果

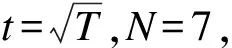
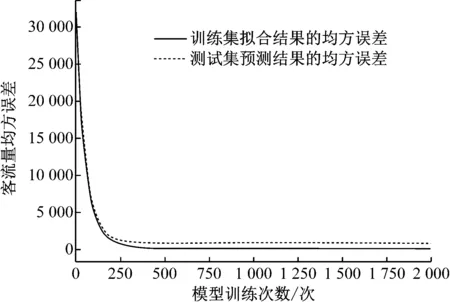
图2 客流量均方误差与模型训练次数的关系

图3为样本中每个属性特征参数对预测结果的贡献度的排名。由图3可知，客流量均值对模型每次训练的特征贡献度较大，节假日、工作日及周末3个参数的特征贡献度靠后。特征贡献度靠后不代表该特征不重要。分析认为，以上多个特征相关度较高(如周末与星期特征之间信息量存在重叠)，故无法对模型产生更大的影响。而节假日所对应的样本较少，通常放在回归树底层作为最后考虑，因此其贡献度较低。

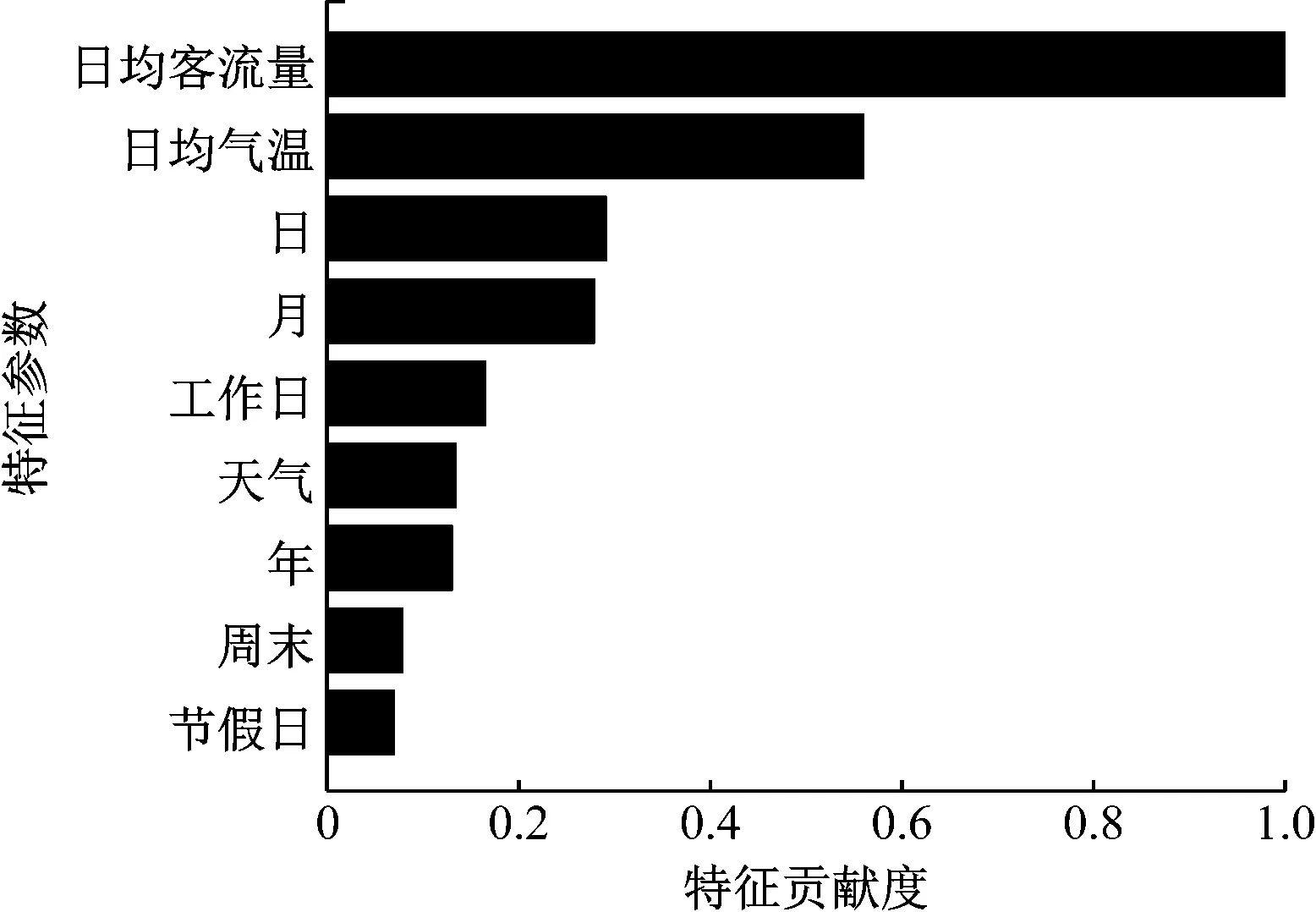
图3 样本中不同属性特征参数对预测结果的特征贡献度

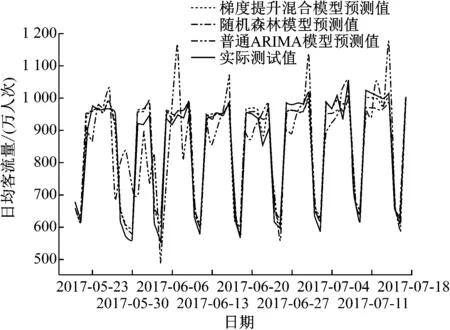
图4 客流量预测值与实测值

图4为从2017年5月20日至7月17日客流量的模型预测结果与实际值。由图4可见：随机森林模型和梯度提升模型的预测效果高于无特殊处理的ARIMA模型，梯度提升及随机森林预测结果基本符合实际客流的变化趋势，梯度提升混合模型的预测结果相较于随机森林有进一步的提升。

对梯度提升模型的部分预测结果进行分析(见表3)。预测结果涵盖节日、工作日与周末的预测客流。分析发现，个别日期实际客流与预测客流存在较大误差。这是训练集特征不够完善引起的，应还存在其他未被考虑的客流影响因素。大多数预测结果均能较好匹配实际值变化，且预测误差在可接受范围之内。

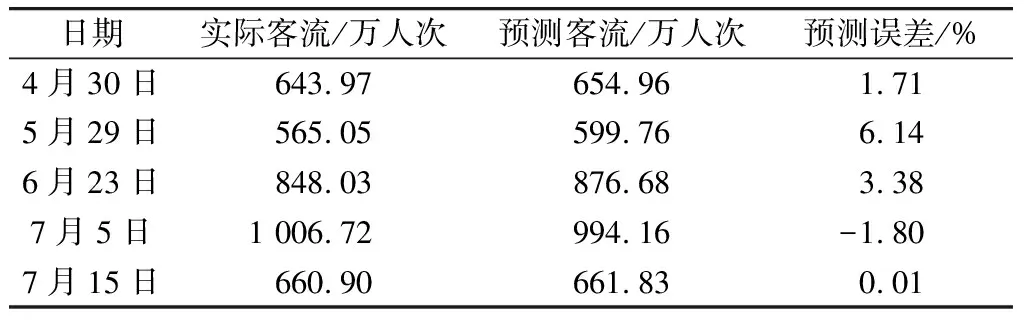
表3 预测结果分析

4 结语

本文分析了梯度提升法的概念和基本原理，将梯度提升法和随机森林的混合模型应用于城市轨道交通客流预测。通过分析北京地铁客流特征及多种影响因素，制定了适用于模型的训练集。试验分析了梯度提升混合模型及其他两种基本模型的预测结果，基于梯度提升的混合模型能实现更高精度。综上所述，梯度提升混合模型能够适用于城市轨道交通客流量的预测与分析，且能取得较好效果。未来研究需进一步完善数据集，扩大样本规模，并结合智慧交通及大数据技术，深入分析城市人口出行规律，为城市轨道交通规划及管理提供新的研究思路及参考。