基于高阶累积量的调制方式识别研究

李 跃 郭兴吉,2 赵 欣,3

(1.西南科技大学城市学院 四川绵阳 621000；2.绵阳师范学院 四川绵阳 621000； 3.绵阳职业技术学院 四川绵阳 621000)

随着现代无线通信技术的高速发展，通信信号的调制方式日益趋于多样化和复杂化。在复杂的通信环境和严重的噪声干扰条件下，不需要依赖任何先验知识就能准确地识别出通信信号的调制方式面临着越来越严峻的挑战[1-2]。文献[3]采用近年提出的八阶累积量结合二、四、六阶累积量，构造了6个特征参数，对MASK，MPSK，MQAM，MAPSK等28种数字调制信号进行了识别，但在信噪比大于20 dB时才能有效识别所有信号；文献[4]提出了一种基于高阶累积量和谱线特征的识别算法，对几种常用于卫星通信的MPSK调制信号和高阶调制信号16APSK进行识别，其中利用高阶累积量完成信号的类间识别，且能有效识别的信噪比大于2 dB。目前常见的方法一般都只在信噪比较大时才能保证较高的识别率。

本文基于高阶累积量方法对8种常见调制信号进行有效识别，计算了APSK信号的理论高阶累积量值，再结合信号的二、四、六、八阶累积量提取了5个特征参数，对2ASK，MPSK，MQAM，MAPSK等8种调制信号进行了有效识别。仿真分析表明，各调制信号的各阶累积量理论计算值与理论仿真值是一致的，且在信噪比较低时也能有效识别信号，验证了该方法的有效性。

1 信号模型

假设接收到的调制信号经过高斯白噪声信道后，已实现载波恢复，经过下变频，FIR滤波后(有时间延迟)输出复基带序列，其表达式为[5]：

(1)

式中，E为信号的平均能量，a(k)为经过平均功率归一化后的信号码元序列，θ为初始相位偏差，n(k)是零均值的高斯白噪声序列，N为样本数据长度。

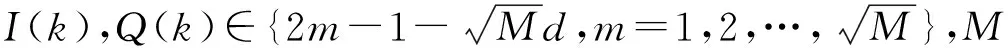
(2)

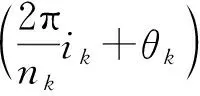
2 特征参数提取

2.1 高阶累积量

一个具有零均值的复随机过程X(n)，其p阶混合矩定义为[9-10]：

Mpq=E[X(n)p-qX*(n)q]

(3)

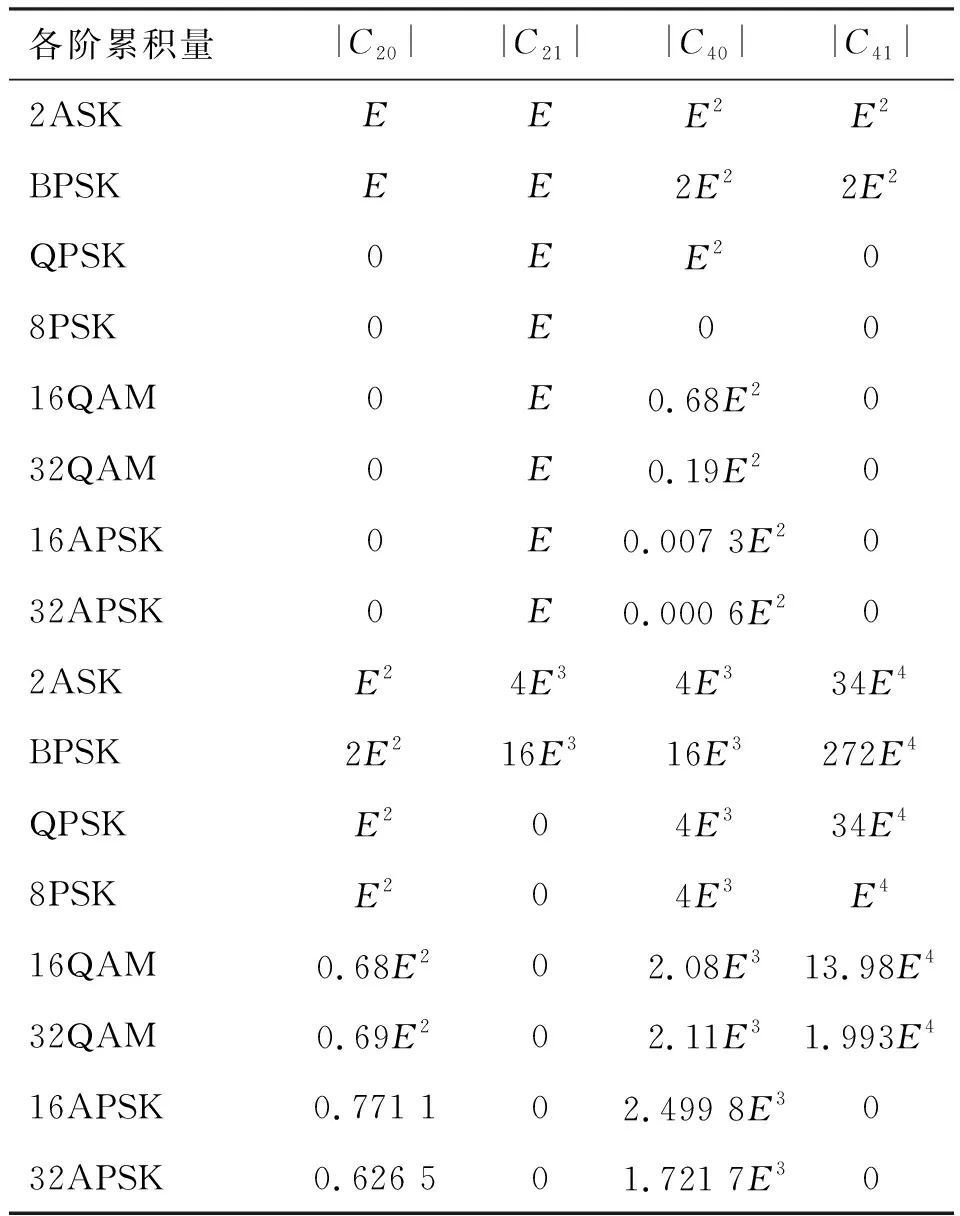
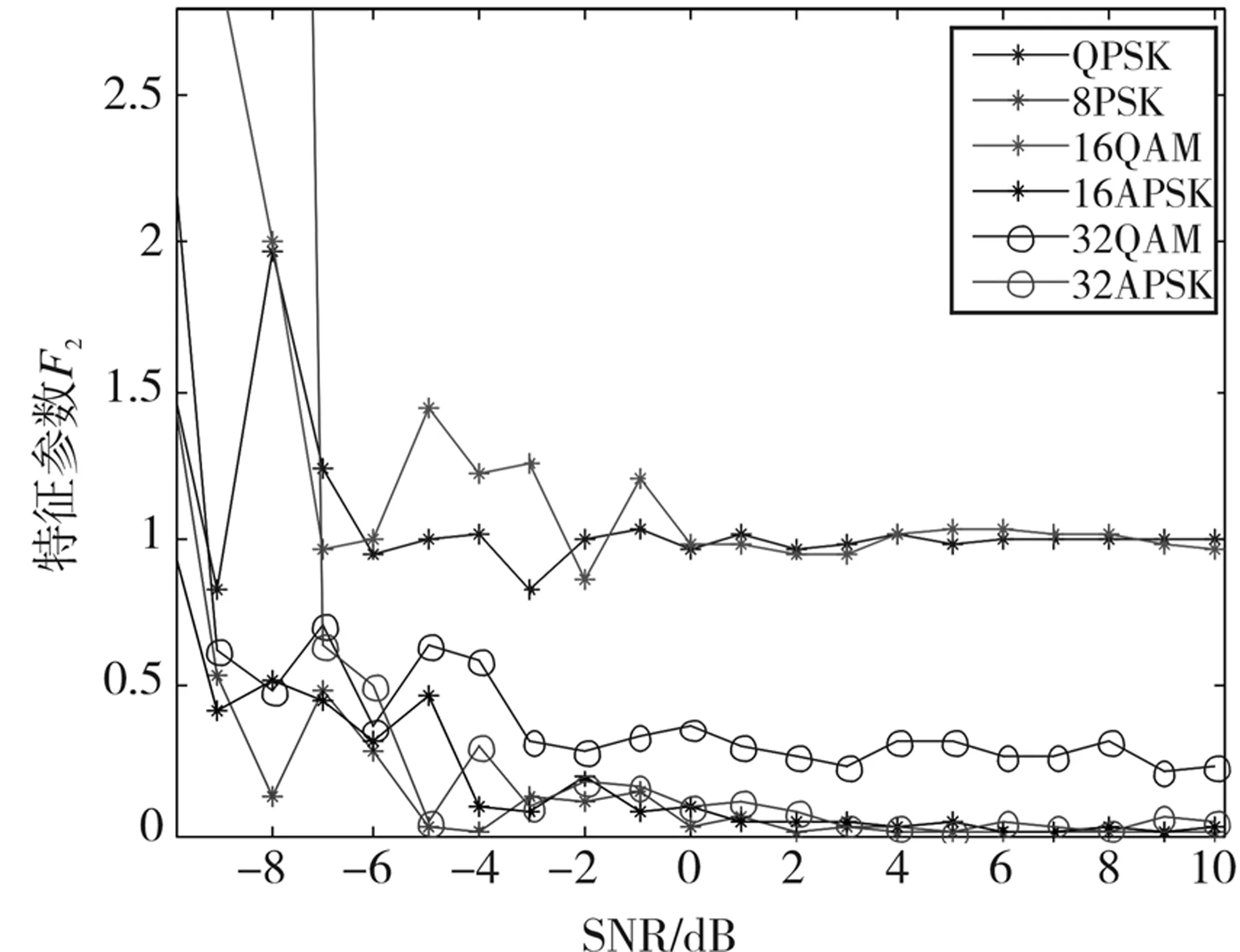
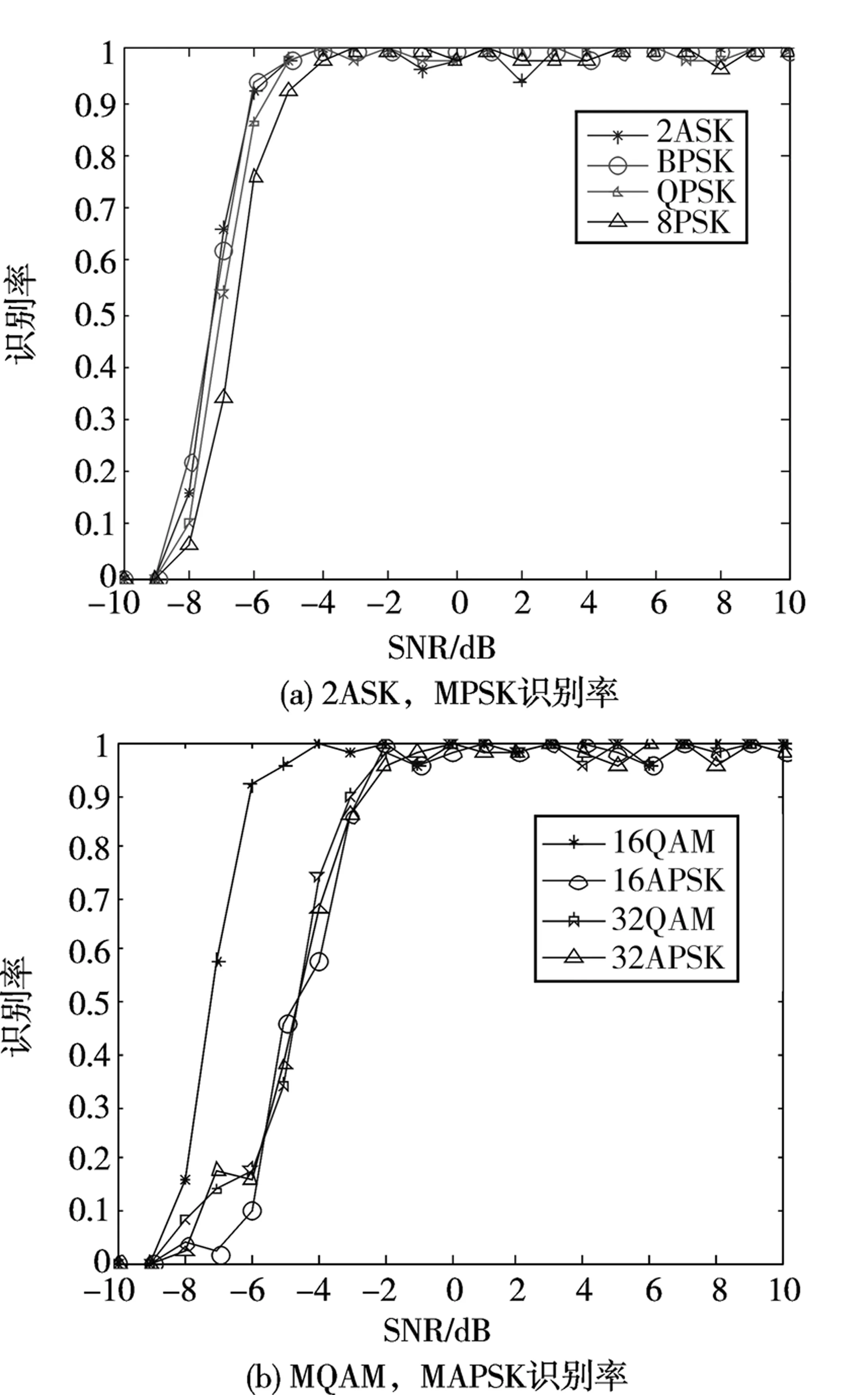
式中，X*(n)表示X(n)的共轭，p表示阶数(q

因为噪声与信号相互独立，根据高阶累积量的性质，高斯噪声的四阶及以上累积量为零，所以可以忽略高斯白噪声的影响。因此高阶累积量有较强的抑制噪声能力。在实际的信号处理中，无法直接计算信号的累积量，需要从有限的接收数据中估计信号的累积量。假设接收的数据为rk，k=1,2,…,N，则根据式(3)可用下面的表达式估计信号的各阶累积量。

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

随着接收数据长度的增加，上述的估计值是渐近无偏的一致估计。

2.2 特征参数提取

根据式(4)-式(11)，设8种调制信号的输入功率为E，即6种信号的二阶累积量C21=M21=E，可计算出功率归一化后的8种调制信号的各阶累积量理论值，见表1。

表1 不同调制方式的各阶累积量理论值Table 1 Theoretical values of each order cumulant of different modulation methods

消除信号输入功率E的影响，根据表1中不同调制方式的各阶累积量的差异情况，构造了如下5个特征参数：F1=|C41|/|C42|，F2=|C40|/|C42|，F3=|C63|2/|C42|3，F4=|C63|,F5=|C42| 。根据各调制方式特征参数值的差异情况，设计分类决策流程图如图1所示。

由图1可知，设置特征参数{F1，F3}的阈值th1识别出2ASK和BPSK信号；设置特征参数{F1，F2，F5}的阈值th2识别出QPSK和16QAM信号；设置特征参数{F1，F2，F5}的阈值th3识别出8PSK信号；设置特征参数{F1，F2，F5，F2}的阈值th4识别出32QAM信号；设置特征参数{F1，F2，F5，F2，F4}的阈值th5识别出16APSK和32APSK信号。

3 仿真分析

本节中，采用matlab仿真来验证所提出的识别算法的性能，分为两部分进行：一是对调制信号各个特征参数值的仿真分析；二是对识别性能的研究。

图1 分类决策流程图Fig. 1 Flowchart of the classification decision

3.1 特征参数仿真

在不考虑载波相位偏差的条件下，通过仿真不同调制信号在码元长度N分别为200,1 000,5 000 时的特征参数值随信噪比的变化曲线，发现在N=5 000 时，曲线波动值最小，收敛性最好，即信号样点数越多，特征值的收敛性越好。取码元序列长度10 000，信噪比设置为-10 dB～10 dB，分别仿真了8种调制方式各特征参数随信噪比的变化曲线。以特征参数值F1,F2为例，特征参数仿真曲线如图3、图4所示。2ASK和BPSK的特征参数F1的理论值都为1，其它调制方式特征参数F1的理论值都为0；QPSK和16QAM特征参数F2的理论值都为1，8PSK的F2理论值为0，32QAM特征参数F2的理论值0.275，16APSK和32APSK的F2理论值分别为0.009和0.000 9。

从图2可以看出，当SNR≥-7 dB时，能有效区分出是2ASK，BPSK信号还是QPSK，8PSK，16QAM，16APSK，32QAM，32APSK信号。由图3可知，当SNR≥-6 dB时，能有效区分出是QPSK，16QAM信号还是8PSK，16APSK，32QAM，32APSK信号。

图2 特征参数F1仿真图Fig. 2 Simulation diagram of the characteristic parameter F1

图3 特征参数F2仿真图Fig. 3 Simulation diagram of the characteristic parameter F2

3.2 识别性能仿真

对8种调制信号的识别性能进行仿真分析，仿真参数设置为：码元长度N=10 000，信噪比SNR为-10 dB～10 dB，阈值设置为：th1={F1,F3}={0.8,27};th2={F1,F2,F5}={0.8,0.75,0.85};th4={F1,F2,F5,F2}={0.8,0.75,0.85,0.2};th3={F1,F2,F5}={0.8,0.75,0.83};th5={F1,F2,F5,F2,F4}={0.8,0.75,0.85,0.2,2.05}，每个信噪比下进行50次仿真，得到各信号识别率如图4所示。

由图4可知，随着信噪比增大，信号的识别率逐渐增大，当信噪比SNR≥-5 dB时，2ASK，BPSK，QPSK，8PSK，16QAM信号的识别率可达90%以上；在信噪比SNR≥-3 dB时，32QAM，16APSK，32APSK信号的识别率可达90%以上。

图4 各信号识别率Fig. 4 Recognition rate of each signal

4 结论

本文研究了基于高阶累积量的调制识别方法，构造了5个特征参数并设计了合理的分类决策树，通过设置阈值对8种常用的调制信号进行了有效识别。计算了MAPSK信号的高阶累积量理论值，对8种调制信号的各特征参数值进行了仿真研究，说明了码元长度对特征参数的影响，仿真结果与理论值一致，验证了特征参数的正确性和合理性。实验结果显示，码元长度N=10 000时，在信噪比SNR≥-5 dB时，2ASK，BPSK，QPSK，8PSK，16QAM信号的识别率可达90%以上；在信噪比SNR≥-3 dB时，32QAM，16APSK，32APSK信号的识别率可达90%以上。本文的识别方法要求码元长度N足够大，导致时间效率较低，有待进一步改进。