探测机器人机械臂的振动分析与结构优化

高伟亚 张俊俊 袁蕾舒 王亚翔

(西南科技大学特殊环境机器人技术四川省重点实验室 四川绵阳 621010)

在核事故和核退役工作中，往往通过机器人替代工作人员完成一些高危险侦测工作，以保护工作人员的人身安全。目前已经有许多国家在核环境机器人运用上取得很大的进步，在核事故中，通过应急机器人进入人类不能进入的工况环境进行辐射剂量侦测、环境因素调查、工况分析，获取有效的现场数据和信息，为制定核废料处理计划提供有效依据[1]。但是因工况导致机器人的任务不同，目前机器人很难适应复杂的工况，故需要根据工况选择或设计特殊环境机器人来完成应急任务。

本研究针对特殊狭窄深井入口的地下辐射空间，入口方孔最大横截面积不超过550 mm×550 mm，深入地下超过10 m，设计了一个特殊机械臂搭载在机器人车体携带的垂直升降装置末端，机械臂携带探测仪器用于探测该危险地下空间的环境状况。对于已经完成设计的机器人机械臂系统，由于运动过程复杂，除了考虑静态特性外，还需要考虑动态特性对系统的影响，因机械臂搭载于车体的升降装置末端，升降装置和末端工具在工作条件下对机械臂施加随时间变化的激励，故需要考虑机械臂整体动态特性。设计研发过程中，借助有限元软件有效模拟机械臂整体动态特性，可以在研发过程中评估设计方案，提高产品研发成功率[1]。

针对机械臂在实际工作中会因受迫振动而影响工作性能，对机械臂进行谐响应分析，并根据分析情况对机械臂进行结构改进，采用参数化建模与Workbench响应曲面分析进行多目标优化，优化过程中考虑了机构的刚度、强度、固有频率和质量，通过选取最佳优化参数作为优化方案，从而提高机械臂的整体工作性能。

1 机械臂的模型建立

1.1 机械臂的虚拟样机建模

通过SolidWorks对机器人系统进行虚拟样机建模，机器人整体结构如图1所示，机械臂安装在机器人车体搭载的5级伸缩机构末端，通过卷扬机控制伸缩机构升降，机械臂通过升降装置和伸缩机构垂直升降进入狭窄入口处的地下空间。机械臂共设计6个关节，机械臂底座安转在升降装置末端，机械臂总长195 mm，机械臂末端处设计有机械和电器快换接口，便于更换工作需要的末端工具。

图1 机器人结构图Fig.1 Robot structure diagram

1.2 机械臂有限元模型的建立

由于机械臂实际工况复杂，无法对其所有工况进行分析，故选取机械臂危险工况对机械臂进行静动态特性分析。在有限元分析过程中为了节省计算量，需要对模型进行简化，忽略原模型的盖板安装螺钉、螺钉孔和补光灯等对分析影响较小的特征[2]。将简化后的机械臂模型导入ANSYS中，设置材料属性，机械臂的各臂体制作材料都选用高性能7075铝合金，7075铝合金的弹性模量E为71.7 GPa，材料密度ρ为2 810 kg/m3，泊松比u为0.33。不考虑谐波减速器和力矩传感器等柔性元件的影响，把谐波减速简化为一个实体，谐波减速器刚轮和法兰制作材料为不锈钢304，不锈钢的弹性模量E为191 GPa，密度ρ为7 900 kg/m3，泊松比u为0.3。

把机械臂各关节减速器法兰与臂体连接面接触类型设置为Bonded，控制机械臂整体网格大小为7 mm，关节6联接法兰处为2 mm，机械臂模型被划分为299 005个节点和164 475个四面体单元，如图3所示。对机械臂进行网格质量检查，如图4所示，网格质量(Element Quality)平均值为0.79，网格质量较高，满足分析要求。

图2 机械臂有限元模型Fig.2 Manipulator finite element model

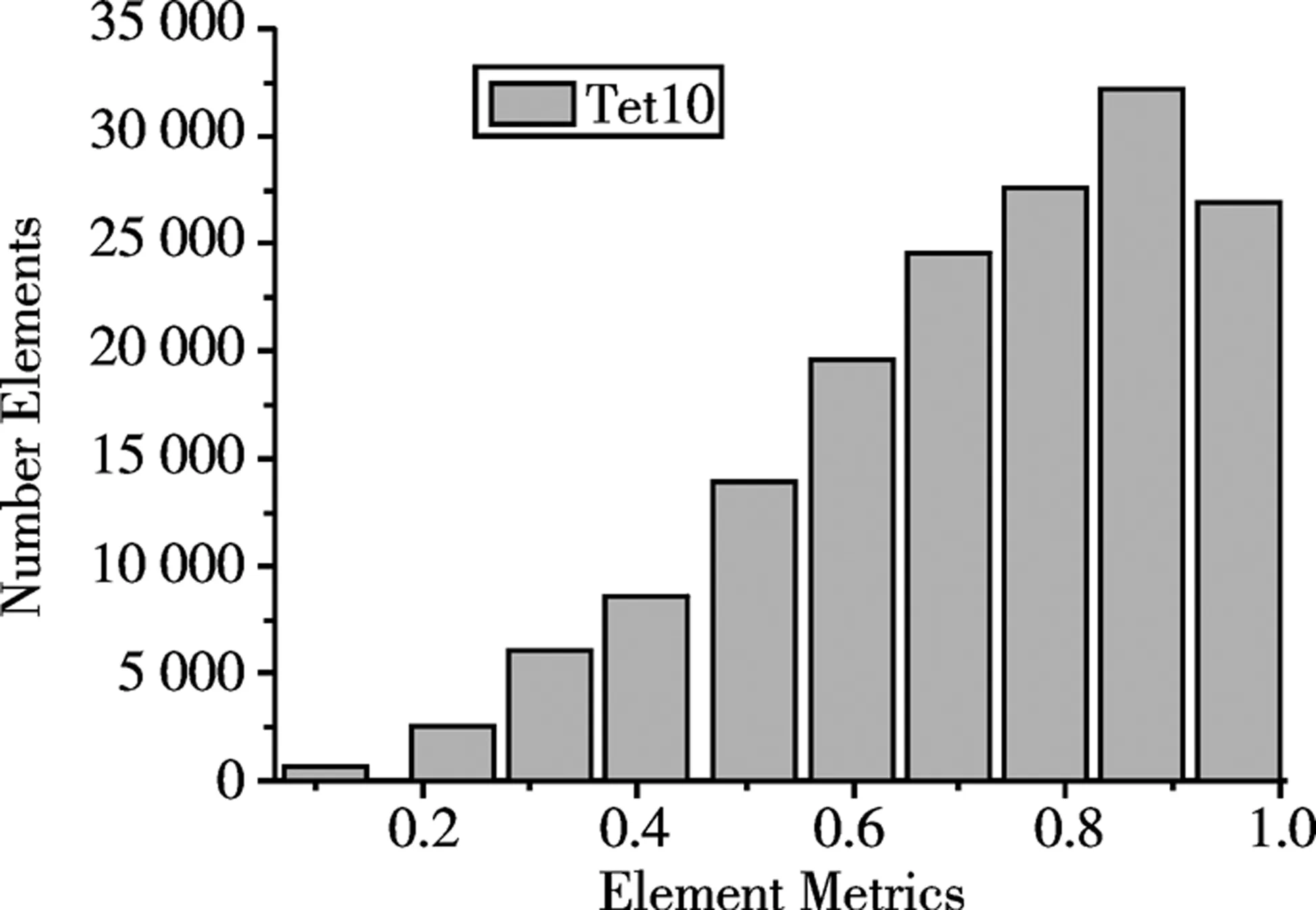
图3 网格质量分析Fig.3 Grid quality analysis

2 机械臂的谐响应分析

2.1 响应分析理论

由于机械臂通过底座固定安装在伸缩机构的末端，机械臂整体系统可以看做一个多自由度系统，谐响应分析的动力学方程为[3-5]：

[M]{x"}+[C]{x' }+[K]{x}={F}

(1)

式中[K]是刚度矩阵，[M]是质量矩阵，[C]是阻尼矩阵，{F}是加载激励力矢量，{x"}是加速度矢量，{x' }是速度矢量，{x}是位移矢量。

谐响应分析中系统受到的激励是周期变化的简谐载荷，频率为ω,那么激励力矢量{F}和位移矢量{x}则为:

{F}={Fmaxeiψ}eiωt=({F1}+i{F2})eiωt

(2)

{x}={xmaxeiψ}eiωt=({x1}+i{x2})eiωt

(3)

式中：ψ是激励力矢量的相位角，则谐响应分析的方程表示为：

(-ω2[M]+iω[C]+[K])({x1}+i{x2})=

({F1}+i{F2})

(4)

谐响应分析计算得出整体结构在激励下任意点的位移或应力对应频率的曲线，用来预测共振并为避免共振提供依据，保证结构能够承受不同频率的简谐载荷。

2.2 机械臂的振动分析

机械臂搭载在移动车体升降装置上，机械臂因升降装置运动产生加速度，升降装置和末端工具会对它施加随时间周期性变化的激励矢量，故对机械臂进行谐响分析是振动分析的关键，采用有限元软件ANSYS得到机械臂在受到随时间周期性变化载荷的幅值曲线[6]，分析机械臂因受迫振动等不利因素的影响，以此为依据对机械臂整体结构优化。

根据机械臂危险工况时末端搭载工作重量，在机械臂末端施加300 N的模拟实际负载，方向与重力方向一致，底座安装处设置为固定副，求出机械臂危险工况下静力特性。对结构进行模态分析，计算机械臂在有预应力的作用下的前六阶固有频率。为了模拟机械臂实际工作受到随时间变化的正弦激励，在机械臂底座施加521 N的正弦激励，相位角为0°，在机械臂关节6施加89 N的正弦载荷，相位角为60°，机械臂受到的激励大部分频率均为0～10 Hz，故频率范围为0～100 Hz，采用模态叠加法进行分析计算。

经分析得到机械臂静动态特性，最大应力为38.6 MPa，最大应变为0.938 mm，前六阶模态如表1所示。图4为关节6末端联接法兰处3个自由度的振幅变化曲线，从图4可以看出机械末端联接法兰处X方向和Z方向在激励为10 Hz左右时出现最大振幅，Z方向的最大振幅最大，为7.45 mm，远大于静态受力的位移，Y方向50 Hz左右的激励出现最大振幅，最大振幅较小，为0.003 mm，对机构的影响较小。由于激励矢量方向与Z方向一致，所以振幅较大，严重影响机械臂的工作性能和携带相机进行图像采集，为了提高机械臂工作中的稳定性，需要对机械臂进行结构优化来减小机械臂末端处的振动。

表1 前六阶固有频率Table 1 The first six natural frequencies

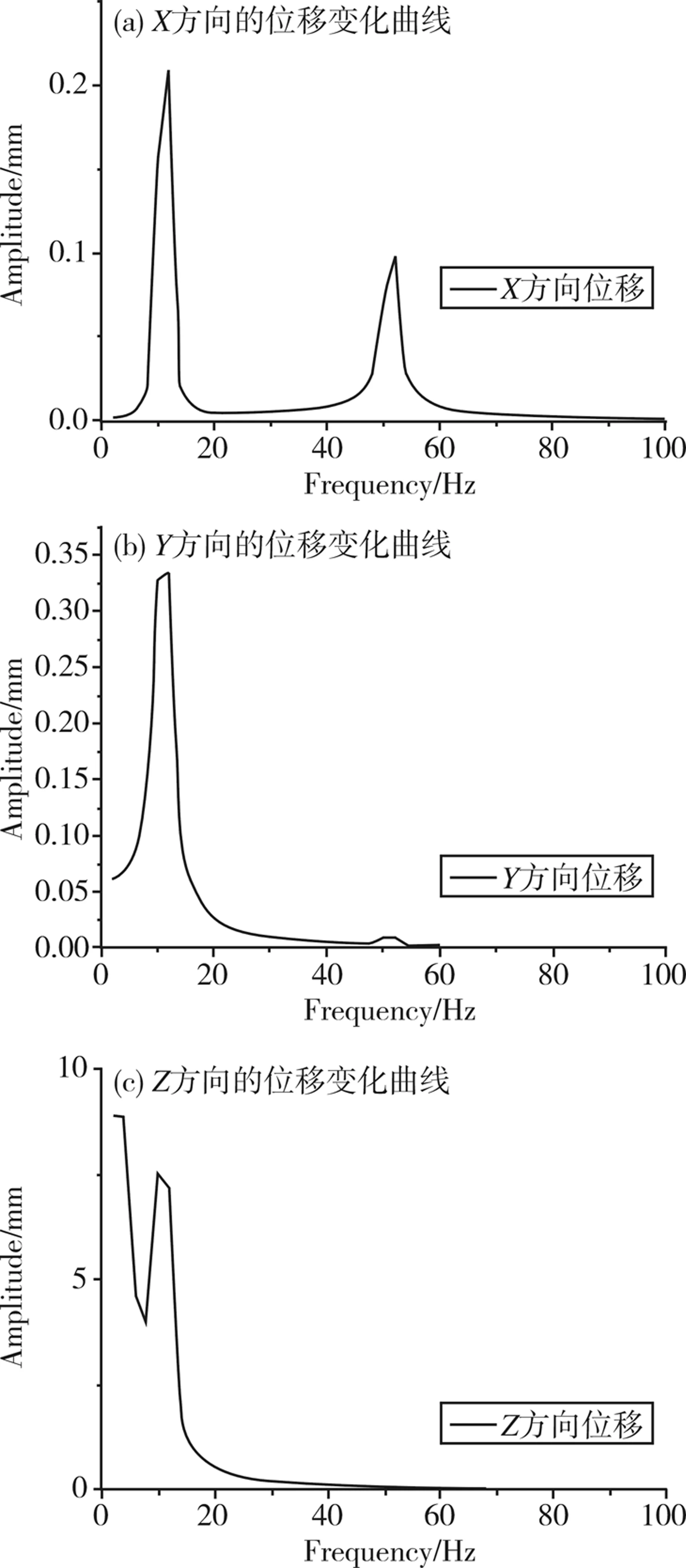
图4 机械臂末端位移变化曲线Fig.4 The curve of the end of arm displacement

3 机械臂的结构优化

3.1 设计变量的选择

为了减小机械臂在受迫振动下的最大位移，需优化结构整体的柔顺度C(式(5))，柔顺度体现了整体结构的应变能力，可以采用储存在结构中的应变能或者结构在外力作用下的做功来表示。如式(6)-式(7)所示，在外载荷的作用下，结构柔顺度相当于刚度的倒数，即位移变化量越小，结构柔顺度越小。

(5)

式中Ku=F则

(6)

(7)

式中u是节点位移矩阵，F是激励载荷，ε是在激励载荷作用下的位移。

由于机械臂整体应力较小，且需要考虑机械臂内部电机、减速器、鱼眼相机的安装，故采用对机械臂连杆主梁部分设计减重孔来优化结构，对机械臂臂体质量较大、应力较小的关节2和关节3臂体主梁部分增加减重孔来减小机械臂的结构柔顺度。减重孔的参数模型如图5所示，减重孔的形状由8个设计变量Pi(i=1,2,…4)决定。

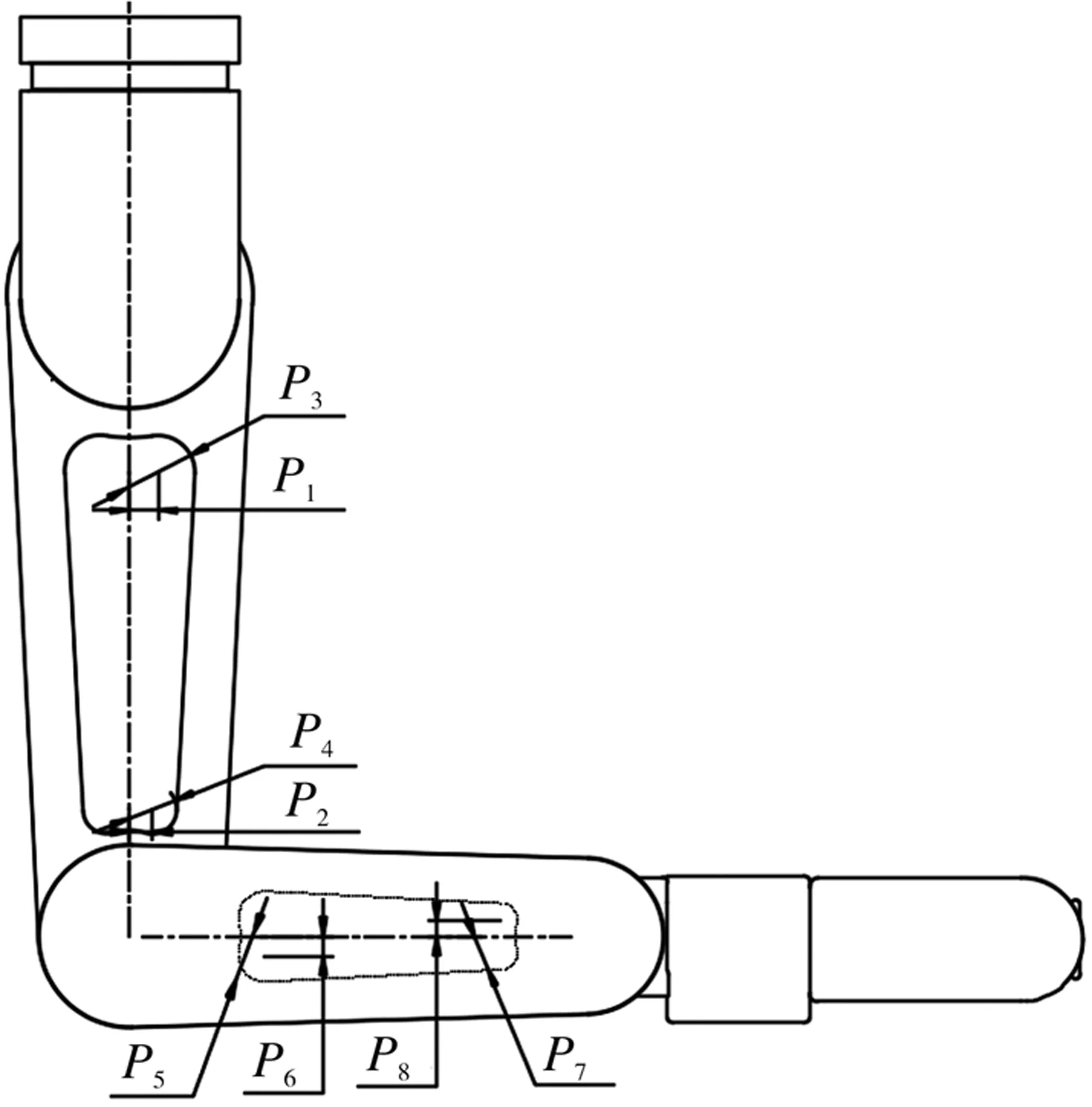
图5 优化参数模型Fig.5 The Optimized parametric model

结构静动态特性的灵敏度分析表示各个设计变量对结构静动态特性的敏感程度，因设计变量较多，在优化设计前，通过灵敏度分析来选择结构的优化参数，减少优化设计的计算量[7]。灵敏度可以表示为：

(8)

式中：ui是结构性能参数，在谐响应分析中为质量、应力和位移；bj是结构设计参数，在分析中可以表示为距离和直径。

根据优化目标分析机械臂结构对最大位移、质量和应力的敏感程度，分析结果如图3(b)所示，P1,P3,P6,P7对Z方向的位移灵敏度相对较大，各设计变量与对应的臂体质量的灵敏度都很小，故选取P1,P3,P6,P74个变量作为优化实验的设计变量。

图6 优化参数对臂体质量和位移的灵敏度Fig.6 Sensitivity of optimized parameters to arm mass and displacement

3.2 机械臂优化设计

通过目标驱动优化分析方法设计优化实验[8-10]，以最小位移为主要优化目标，fz(x)为目标函数Z方向的最大位移，最大不超过2 mm，min Mass2为目标函数机械臂关节2连杆的质量，min Mass3为目标函数机械臂关节3连杆的质量，σmax是最大应力(Equivalent Stress Maximum)，小于材料的屈服强度σs，小于最大应变2 mm。设计变量考虑机械臂臂体主梁轮廓和电机、减速器安装孔位置，取P1：34～42 mm，P3:26～33 mm，P6:27～33 mm，P7:32～36 mm，则优化数学模型为：

使用Workbench响应曲面优化方法的实验设计技术对机械臂优化设计，经运算生成25个实验样本，得到设计变量和末端最大位移的响应曲面如图7所示，当P3为30 mm左右振幅峰值到达最大，其余3个变量与振幅峰值为负相关关系，变量值越大振幅越小。如图8所示，由设计试验点可以看出第25组实验参数使振幅峰值达到最小且P3避开了峰值点，为1.72 mm，达到优化目标。故选取第25组设计变量(41,32,32,35 mm)，此时关节2臂体和关节3臂体分别由18.8，12.29 kg减小至13.3，8.71 kg，相比原结构减小了28.3%和29.5%。

图7 位移的响应曲面Fig.7 Displacement response surface

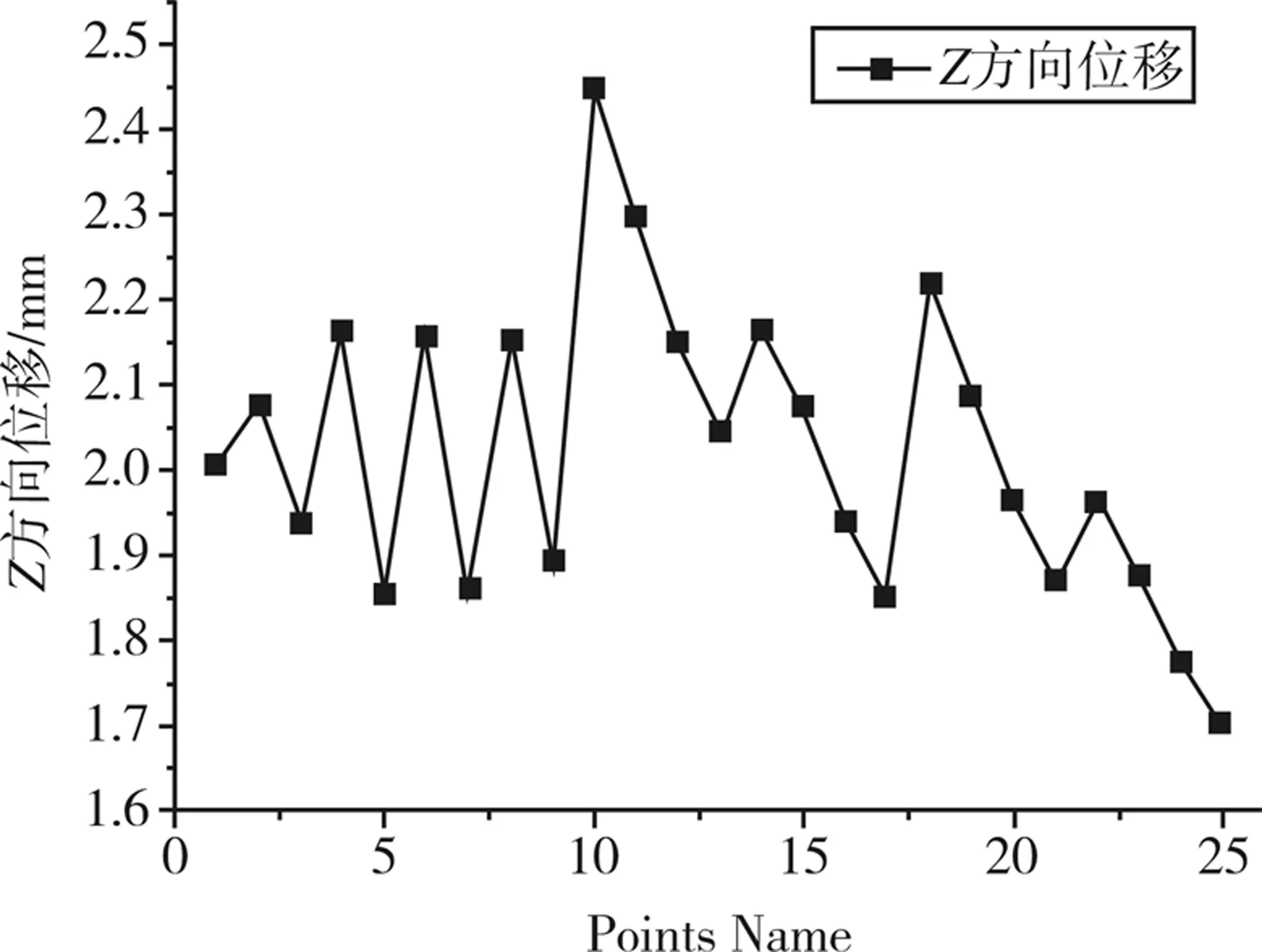
图8 试验点最大振幅Fig.8 Maximum amplitude of test point

4 改进后机械臂的振动分析

对改进后的机械臂进行振动分析，频率范围设置为0～200 Hz，求解后得到机械臂最大应力出现在30 Hz附近，由38.6 MPa减小到30.5 MPa。前六阶固有频率如表2所示，各阶固有频率均有大幅增加，后三阶增幅较大，有效避免了10 Hz以下的低频共振，机械臂整体动态特性明显提高。得到优化后关节6末端联接法兰处3个方向的振幅变化曲线如图9所示，优化后Z方向在受迫振动下的振幅峰值由7.54 mm减小到1.71 mm，峰值出现在第二阶固有频率附近，X,Y方向的振幅峰值也大幅减小，最大峰值发生在第六阶固有频率附近。如图10所示，末端最大位移为1.4 mm，小于设计要求2 mm，达到优化目标。分析表明优化方案减小了机械臂末端的最大位移，有效降低了机械臂末端的振动，提高了机械臂整体动态性能。

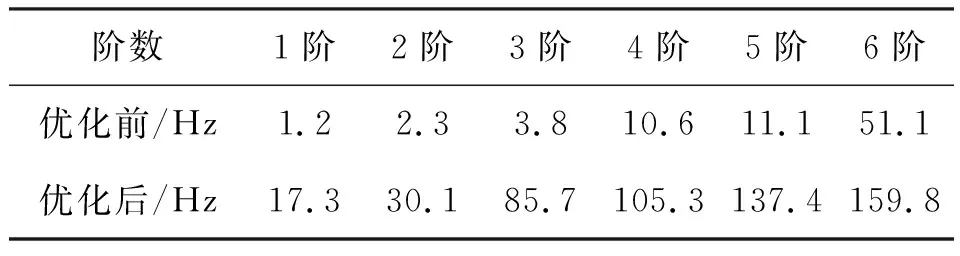
表2 优化后前六阶固有频率对比Table 2 Comparison of the first six natural frequencies

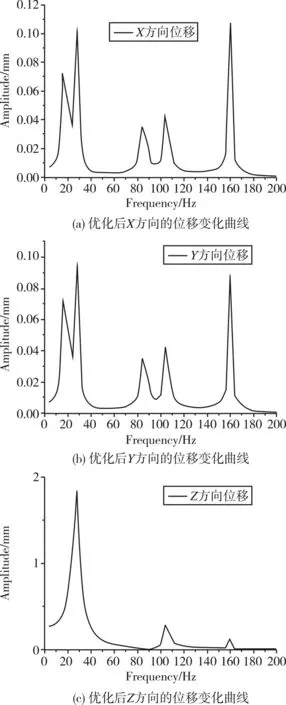
图9 优化后的机械臂末端的位移变化曲线Fig.9 The curve of the end of arm displacement after optimization

图10 优化后机械臂变形云图Fig.10 Manipulator deformation cloud after optimization

5 结束语

通过有限元软件对探测机器人机械臂进行振动分析，得到机械臂应力分布、前六阶固有频率和在受迫振动下机械臂末端的振幅变化特性。根据分析结果对机械臂进行了结构改进，通过对机械臂参数化建模，采用响应曲面优化方法设计优化实验，并选取最佳优化方案，优化改进使机械臂整体质量减小了5.1%，优化后机械臂最大应力减小，前六阶固有频率均增大，有效避免了低频共振，末端Z方向位移峰值由7.54 mm减小至1.71 mm。优化改善了机械臂结构质量分布，减小了结构柔顺度，有效减小了受迫振动对机械臂工作的损害，可为探测机器人机械臂的实物样机制作提供依据。