带螺旋侧板立管两向涡激振动的试验研究

周 阳， 黄维平， 杨 斌， 潘 冲， 宋泽坤

(1.浙江海洋大学 港航与交通运输工程学院，浙江 舟山 316000;2.中国海洋大学 山东省海洋工程重点实验室,山东 青岛 266100;3.国家海洋局第二海洋研究所 工程海洋学重点实验室,杭州 310012)

在工程领域中，涡激振动现象带来了非常多的问题，对它进行的研究工作也十分广泛。物体在一定流速的空气、水等流体作用下，尾部会产生交替的旋涡，导致物体两侧形成脉动的压差，从而引起结构的振动，如高压电缆，桥梁，电视塔，海洋立管等。海洋立管是海洋平台的重要组成部分，用于海底油气的传输，海洋立管的涡激振动会引起结构的疲劳破坏，如何抑制海洋立管的涡激振动是目前立管研究的热点问题之一[1-4]。

主动控制和被动控制是抑制涡激振动最常用的两种方法。主动控制方法对结构的外部流场进行监测，采用自动控制原理对流场进行扰动，从而实现旋涡泄放的有效控制，该类方法有声激励系统、结构自主旋转振动、抽吸与喷吹等。被动控制方法则是通过改变结构表面几何形状，达到改变结构周围流场的目的，从而实现旋涡泄放的有效控制，该类方法有螺旋侧板，导流板，整流罩等，其中螺旋侧板是深水立管涡激振动的主要抑制装置[5-7]。早期已经有诸多国内外学者通过试验方法对螺旋侧板的特性进行了研究[8-11]。Korkischko等[12]采用模型试验的方法，对固定串联立管涡激振动时的螺旋侧板抑制作用进行了研究，讨论了螺旋侧板导程对立管涡激振动的抑制作用，还通过模型试验的方法研究了动态表面边界层对立管涡激振动的抑制作用，研究发现采用动态表面边界层后立管尾流变窄，横流向波动速度减小[13]。Huang等[14]采用模型试验的方法，对多种并联和串联排列方式的带螺旋侧板立管涡激振动时的升阻力进行了研究，研究发现螺旋侧板能显著降低上游立管的涡激力，但是对下游立管的效果并不明显。苑健康等[15-16]通过CFX数值模拟软件对带螺旋侧板立管的绕流问题进行了研究，指出螺旋侧板使立管不同截面处的涡激力不同步，从而实现抑振的效果。翟云贺等[17]提出了三种海洋立管涡激振动的抑制装置并进行了模型试验研究，结果表明这三种装置均有抑振作用。王亚非等[18]通过Fluent数值模拟软件对不同导程螺旋侧板的立管模型进行了绕流分析，研究发现螺旋侧板导程越大抑制涡泄的效果越好。以往研究中很多只是关于圆柱绕流问题的，并不是真实的涡激振动问题，而且大多只注重横流向的涡激振动研究，很少对顺流向的振动进行比较分析。一般模型试验和数值模拟研究所采集的数据有升阻力、结构位移和动态应变等，本文试验所采集的为立管模型的动态应变，该参数是反应结构发生疲劳损伤的最直接参数。

在前人研究基础上，本文对覆盖3片螺旋侧板的海洋立管进行模型试验，对3种不同导程螺旋侧板的立管在不同雷诺数下进行两自由度涡激振动试验，并引入光滑立管模型进行比较，研究螺旋侧板对立管外部流场，涡泄以及涡激振动特性的影响。

1 模型试验

1.1 理论基础

在一定均匀流速下，直立圆柱体后方会形成交替的涡旋，涡旋产生的脉动压力差会导致结构发生振动，此时，按受力形式可以将圆柱体所受力分为拖曳力和升力，经典的拖曳力FD计算见式(1)，升力FL计算见式(2)

(1)

(2)

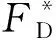
根据现有的实验和理论分析可知，脉动拖曳力系数和升力系数随时间呈正弦变化，可见脉动拖曳力和升力是导致海洋立管疲劳破坏的直接原因，其中脉动拖曳力影响立管顺流向弯曲交变应力，升力影响立管横流向弯曲交变应力。

圆柱体发生涡激振动时，影响其涡旋脱落特征及涡激振动特性的几个主要无因次参数包括[19]：雷诺数Re=U·D/υ，约化速度Ur=U·Tn/D，Strouhal(斯托哈尔)数St=fv·D/U，频率比fv/fn等。其中υ为水的运动粘滞系数；Tn为圆柱在静水中的固有周期；fn=1/Tn为固有频率；fv为涡泄频率。

对于单根圆柱体，研究表明Re在150～1.5×105范围内，柱后出现交替的涡旋脱落，频率为

(3)

对于斯托哈尔数St，根据罗斯柯(A.Roshko)1954年的试验，在Re=200～1.5×105范围内，St数约等于常数0.21。

1.2 试验设计

该试验依托山东省海洋工程重点实验室完成，其试验水槽长30 m，宽59 cm，深95 cm，可以产生流和规则波，最大流速度0.3 m/s。

为了研究螺旋侧板的导程对立管涡激振动的抑制效果，试验分别采用了导程为管径的3.5倍，6倍和9倍的3组带螺旋侧板立管，而它们的侧板高度均为0.25D，侧板厚度均为0.1D，立管模型及试验在位情况见图1，同时引入一组不带螺旋侧板的光滑立管模型进行比较。4组立管模型均采用1 m高，直径为20 mm，壁厚为4 mm的有机玻璃管，上下两端分别用钢板固定，模拟固支梁，不考虑边界条件对结构涡激振动的影响。

图1 试验模型Fig.1 Test models

本文试验数据的采集采用应变片测量的方式，通过动态应变仪直接采集立管模型的表面应变作为结构振动特性指标，在立管跨中环向每隔90°安装应变片，每组立管4个应变片，两个对边应变片组成半桥测量系统，用来测量横流向和顺流向应变，应变与结构应力相对应，直观地反应涡激振动所引起的结构应力循环。

4组立管模型分别在11组流速下进行涡激振动试验，相应的雷诺数范围为65～3 360，如表1所示。考虑到流体试验可能存在的迟滞效应[20]，各组立管模型进行试验时，流速先由小到大，在每组流速下采集3次应变数据，采样频率为1 000 Hz，每次采集时长为30 s，完成后流速再由大到小，同样在每组流速下采集3次应变数据。

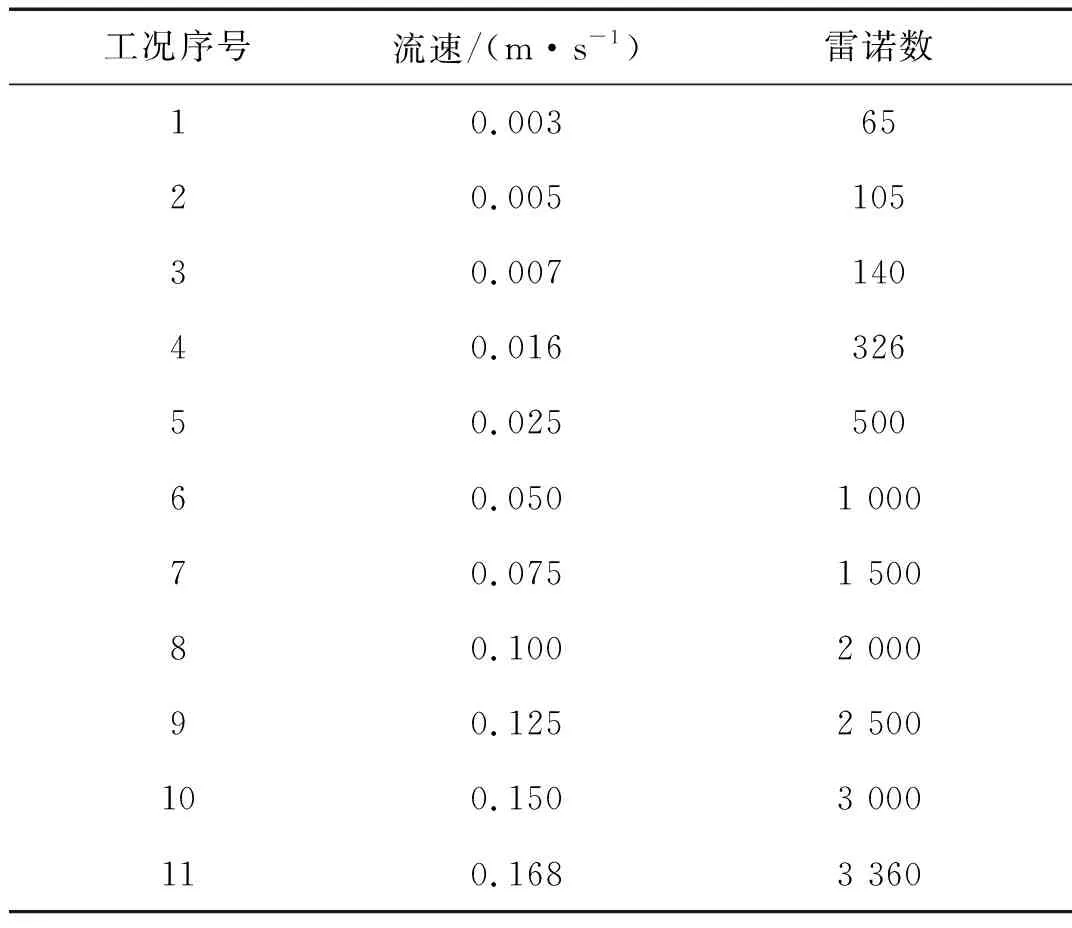
表1 试验工况表Tab.1 Table of test cases

2 结果分析

2.1 立管模型振动特性参数

试验首先对立管在空气和水中的固有振动特性进行研究，对两端固定的立管分别在空气和水中进行冲击激励，可以得到相应的自由振动衰减图，如图2所示，根据自由振动衰减法，可以计算得到立管的衰减系数，以及相应的阻尼系数，如式(4)所示

(4)

式中：δ为对数衰减率；N为两个位移峰值相隔N个周期；ξ为阻尼比；λ为无阻尼情况下结构固有圆频率；λd为有阻尼情况下结构固有圆频率；Td为有阻尼情况下结构固有周期。

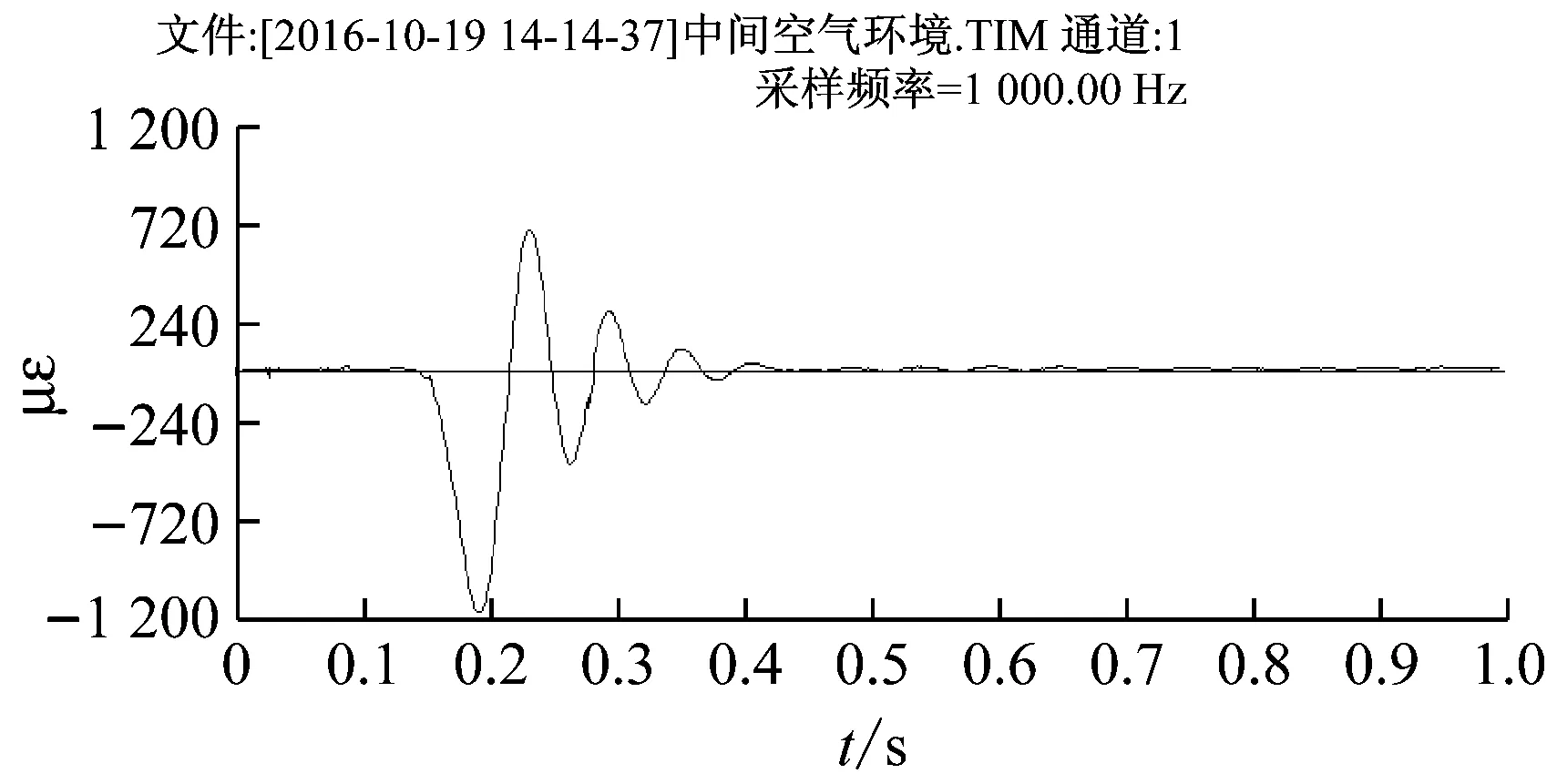
图2(a)为光滑立管在空气中自由振动的应变-时间图，从图中可得衰减振动周期Td=0.051 s，对数衰减率δ=0.63，阻尼比ξ=0.10，立管固有频率为19.6 Hz。

图2(b)为光滑立管在水中自由振动的应变-时间图，从图中可得衰减振动周期为Td=0.063 s，对数衰减率δ=1.0，阻尼比ξ=0.16，立管固有频率为15.8 Hz。

对比光滑立管在空气和水中的振动参数，可以看出立管衰减振动周期在水中要比在空气中长，对数衰减率、衰减系数与阻尼比在水中要比在空气中大，这是由于水的粘度比空气大引起的。表2为4组试验立管在空气和水中的固有频率，从中可以看出，在水中的管频率都有不同程度的减小。

(a) 空气中自由振动响应

(b) 水中自由振动响应图2 光滑立管自由振动图Fig.2 Free vibration of the bare riser表2 模型固有频率Tab.2 Natural frequency of test models

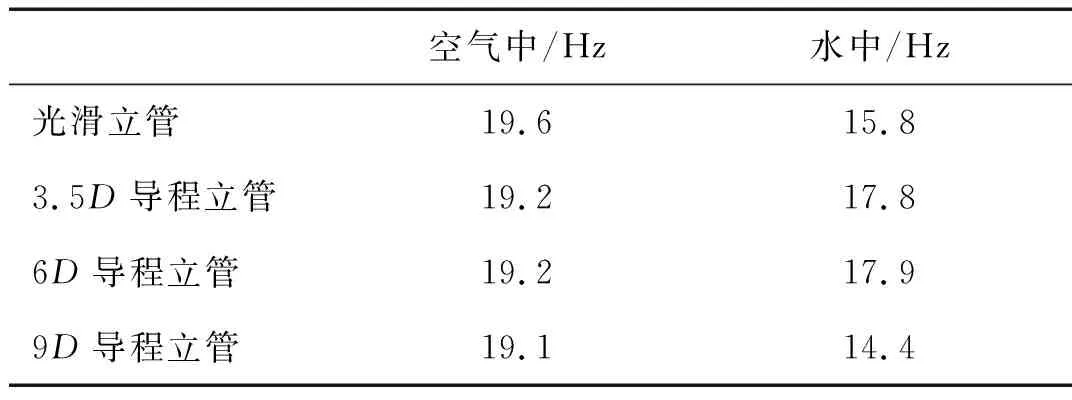
空气中/Hz水中/Hz光滑立管19.615.83.5D导程立管19.217.86D导程立管19.217.99D导程立管19.114.4

2.2 两向涡激振动响应分析

图3为Re=1 500时，4组立管中部的横流向与顺流向振动响应叠加图，从图中可以看出，4组立管横流向与顺流向振动的相位差均为90°，可见立管的振动轨迹为椭圆形，其中图3(a)对应的是极扁的椭圆轨迹，也可以认为其属于“一”字形运动轨迹。本试验中未出现两向振动周期关系为两倍的情况，其中两倍周期关系对应月牙形或“8”字形振动轨迹。椭圆形振动轨迹和“8”字形振动轨迹是涡激振动研究中较常见的情况[21-22]，本试验只有椭圆形振动轨迹而没有出现“8”字形振动轨迹一是由于试验的流速范围并不大，只是在较低的雷诺数区间进行试验，二是由于不同的质量比、固有频率等因素都会对涡激振动的轨迹产生影响。

图4为不同雷诺数下不同导程螺旋侧板立管两向涡激振动响应轨迹示意图，每一圈代表一组雷诺数，从图中可以看出，螺旋侧板对立管涡激振动的轨迹有一定影响，其中光滑立管和带侧板立管之间的振动轨迹差异较大，而各不同导程螺旋侧板立管之间的振动轨迹差异较小，光滑立管的振动轨迹为长短轴相差很大的扁椭圆，而带侧板立管的振动轨迹接近正圆。

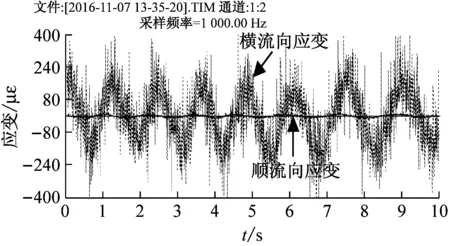
(a) 光滑立管

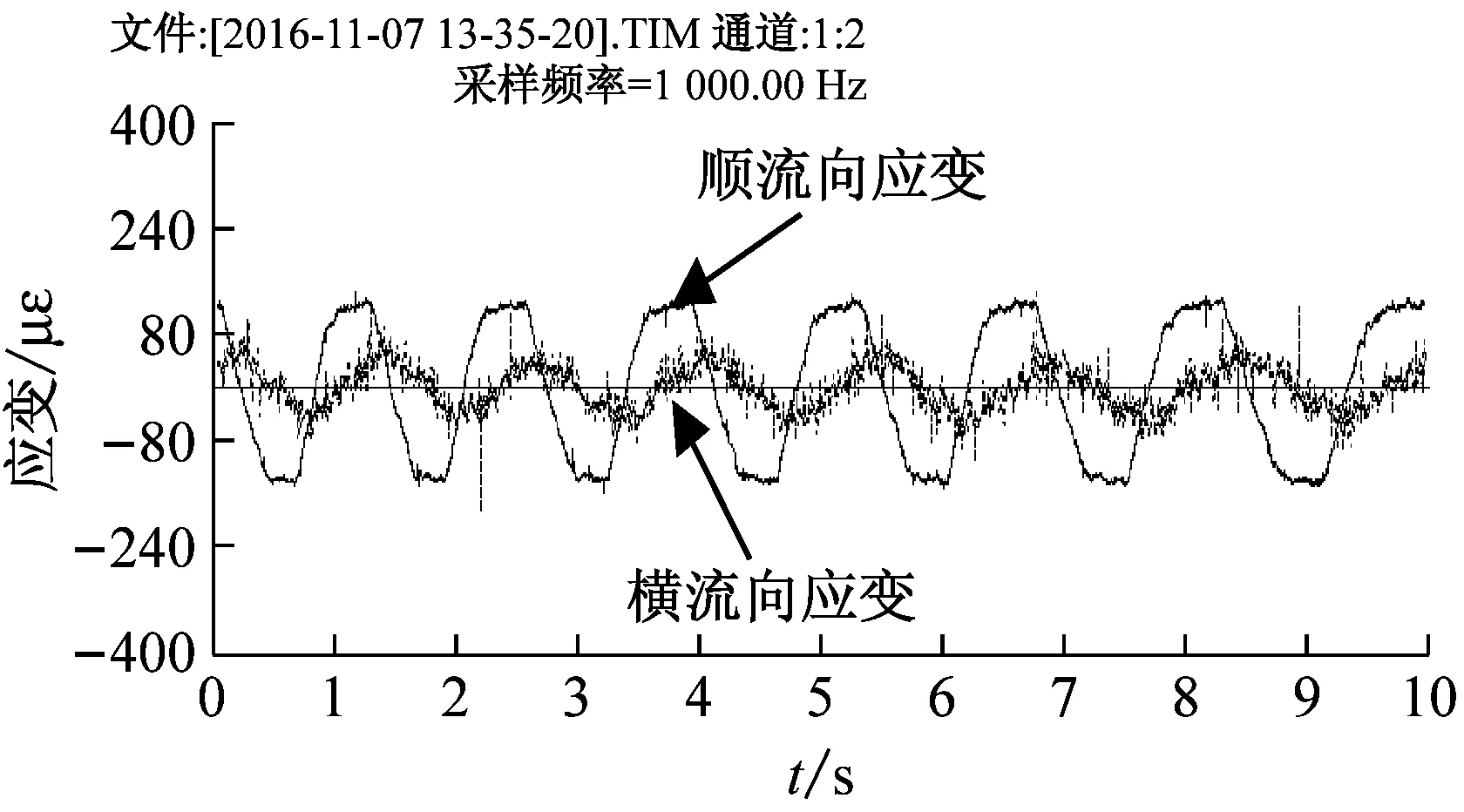
(b) 3.5D导程立管

(c) 6D导程立管

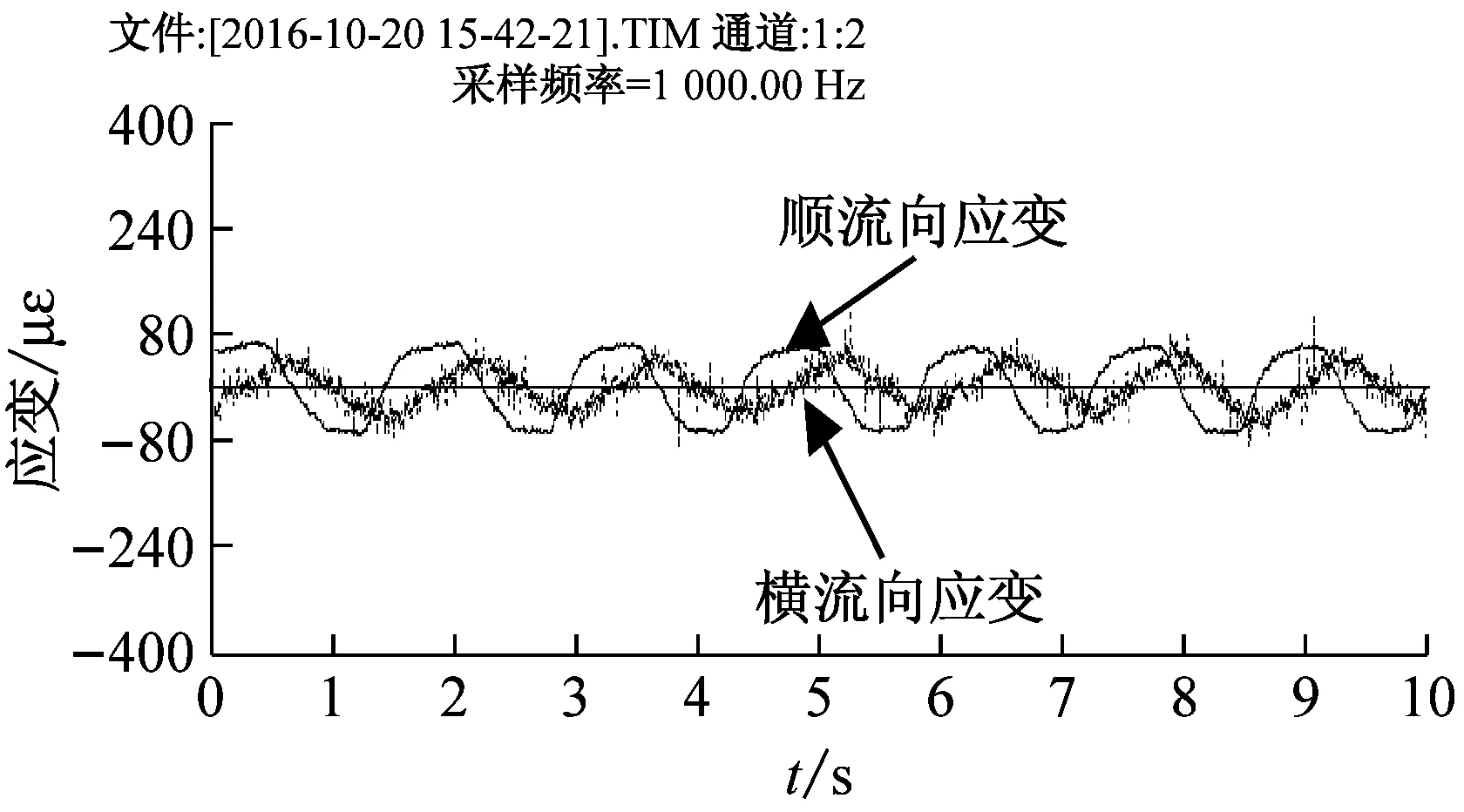
(d) 9D导程立管图3 Re=1 500时，立管两向涡激振动叠加图Fig.3 Re=1 500, vortex-induced vibration of risers in two-degree-of-freedoms

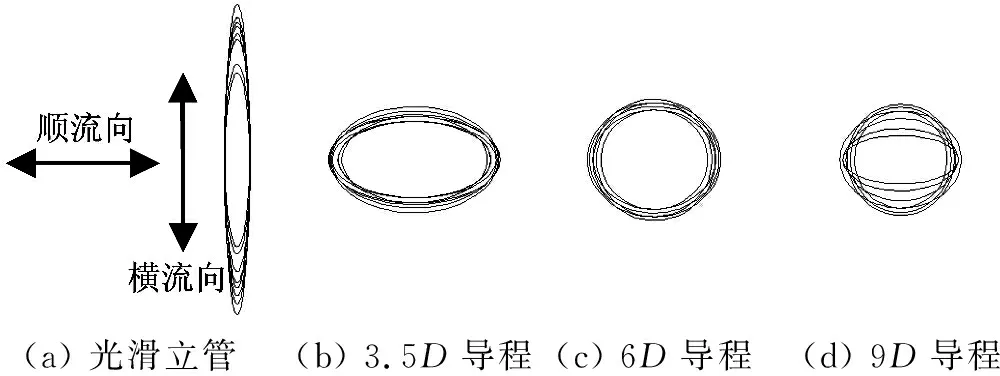
(a) 光滑立管(b) 3.5D导程(c) 6D导程(d) 9D导程

图4 4组立管的振动轨迹示意图

Fig.4 Trajectories of the four models

图5给出了各组立管模型的横流向应变幅值随雷诺数变化的情况，分析可知，同光滑立管相比，带侧板的3组立管模型横流向振动响应明显减小，减小幅度可达70%左右，可见螺旋侧板的存在破坏了沿轴向涡旋脱落的一致性，抑制了立管横流向涡激振动响应。但是，通过图6发现，带侧板立管的顺流向涡激振动响应较光滑立管有一定程度的增加，可见侧板的存在对立管顺流向的振动响应不利。这就使得在选择螺旋侧板时，既要保证能抑制立管横流向振动，又不过度增加顺流向振动响应。对比分析图5和图6的两向涡激振动响应可知，3.5D导程立管的顺流向响应较横流向响应大1.5倍左右，而6D导程立管和9D导程立管的横流向与顺流向响应相差都不大，与图4一致，而且9D导程立管的两向涡激振动响应较其他两组带侧板立管模型的响应要小，可见3组带侧板立管模型中，9D导程的螺旋侧板对立管的涡激振动抑制效果最好。

图5 4组立管的横流向应变Fig.5 Cross-flow responses of the four models

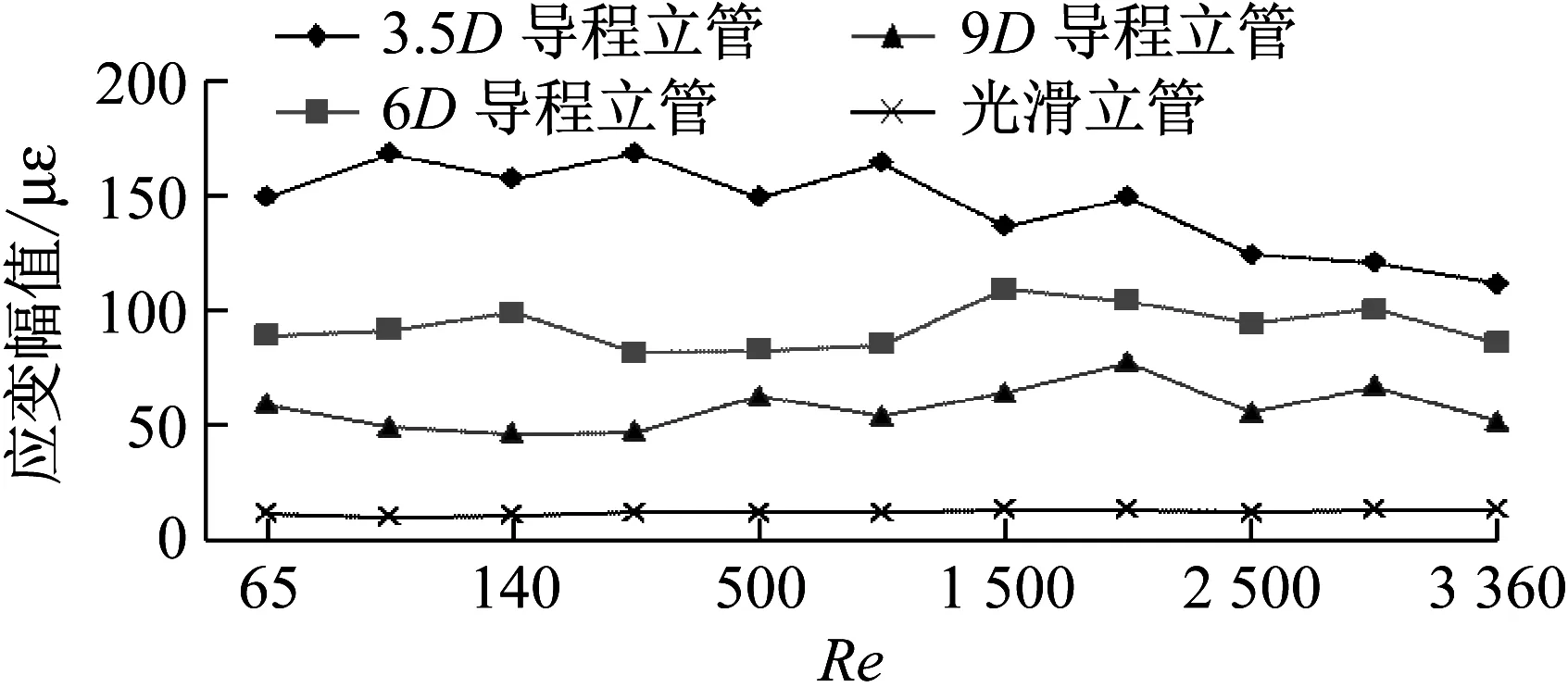
图6 4组立管的顺流向应变Fig.6 In-line responses of the four models

本试验还采用示踪方法对4组立管模型涡激振动时的尾流进行了观测，通过在模型两侧近水面处开孔，模型内部注入示踪剂的方法，实现涡旋泄放的观测。图7为Re=1 500时，4组立管模型的涡旋泄放图，可见光滑立管的涡泄为明显的2S泄放模式，而带侧板立管的涡旋泄放十分紊乱。结合涡激振动响应数据和涡旋泄放情况可知，螺旋侧板的存在可以扰乱流场，影响立管所受拖曳力和升力，最终影响立管的两向涡激振动特性，达到抑制涡激振动的目的。

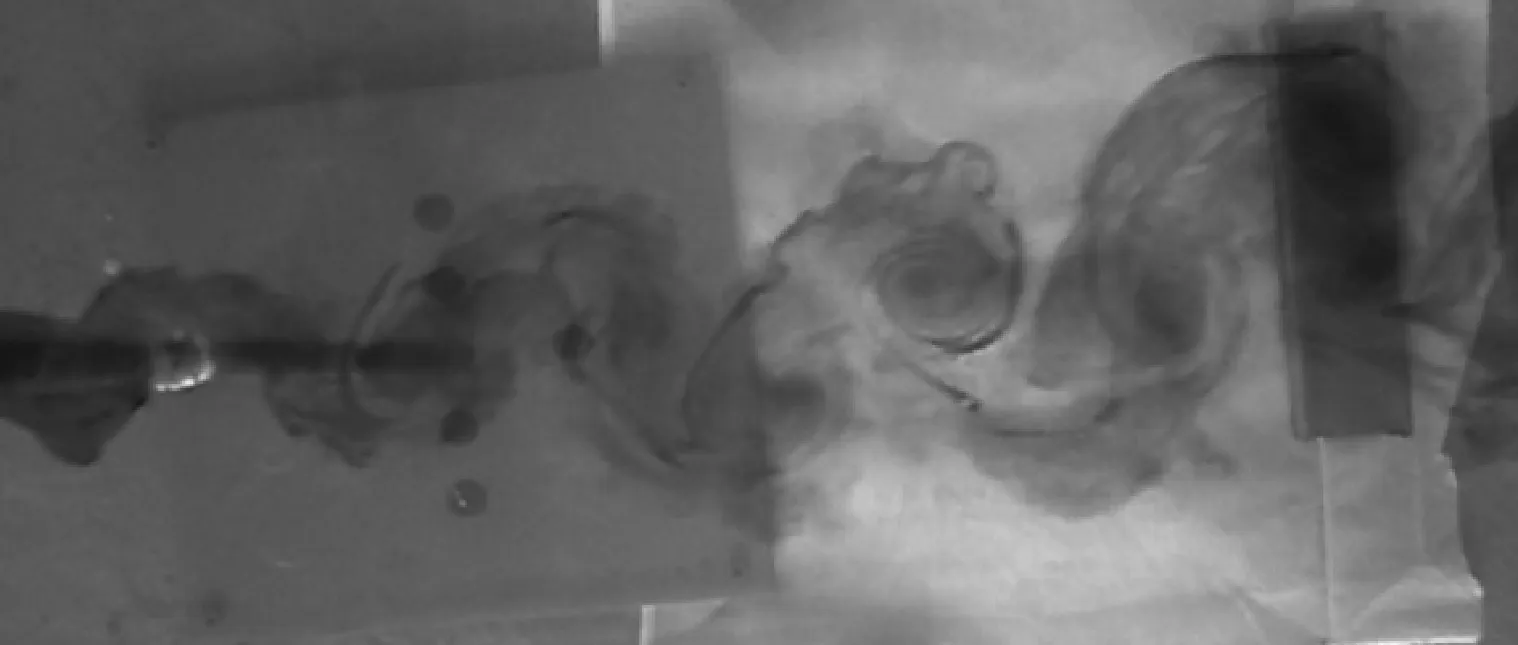
(a) 光滑立管

(b) 3.5D导程立管

(c) 6D导程立管

(d) 9D导程立管图7 立管涡旋泄放图Fig.7 Vortex shedding of risers

2.3 频谱分析及St数计算

对立管模型在不同雷诺数下的的横流向应变时程数据作频谱分析，可以得到相应的频谱图，图8给出了Re=1 500时各组立管的频谱分析图，从图中可以看出，频谱分析图中主要存在三种频率成分，涡旋泄放频率，立管模型自身固有频率，交流供电频率，其中交流供电频率均为50 Hz，模型固有频率同表1相一致。Re=1 500时，光滑立管、3.5D导程立管、6D导程立管、9D导程立管的涡泄频率分别为0.793 Hz、0.702 Hz、0.641 Hz、0.702 Hz。可见带螺旋侧板立管的涡泄频率较光滑立管的涡泄频率要低，其中6D导程立管的涡泄频率降幅最明显，这是由于螺旋侧板的存在变相的增加了立管的水动力直径，导致涡泄频率的降低，与式(3)相符，而且不同导程的螺旋侧板对水动力直径和涡泄频率的影响不一样。

(a) 光滑立管

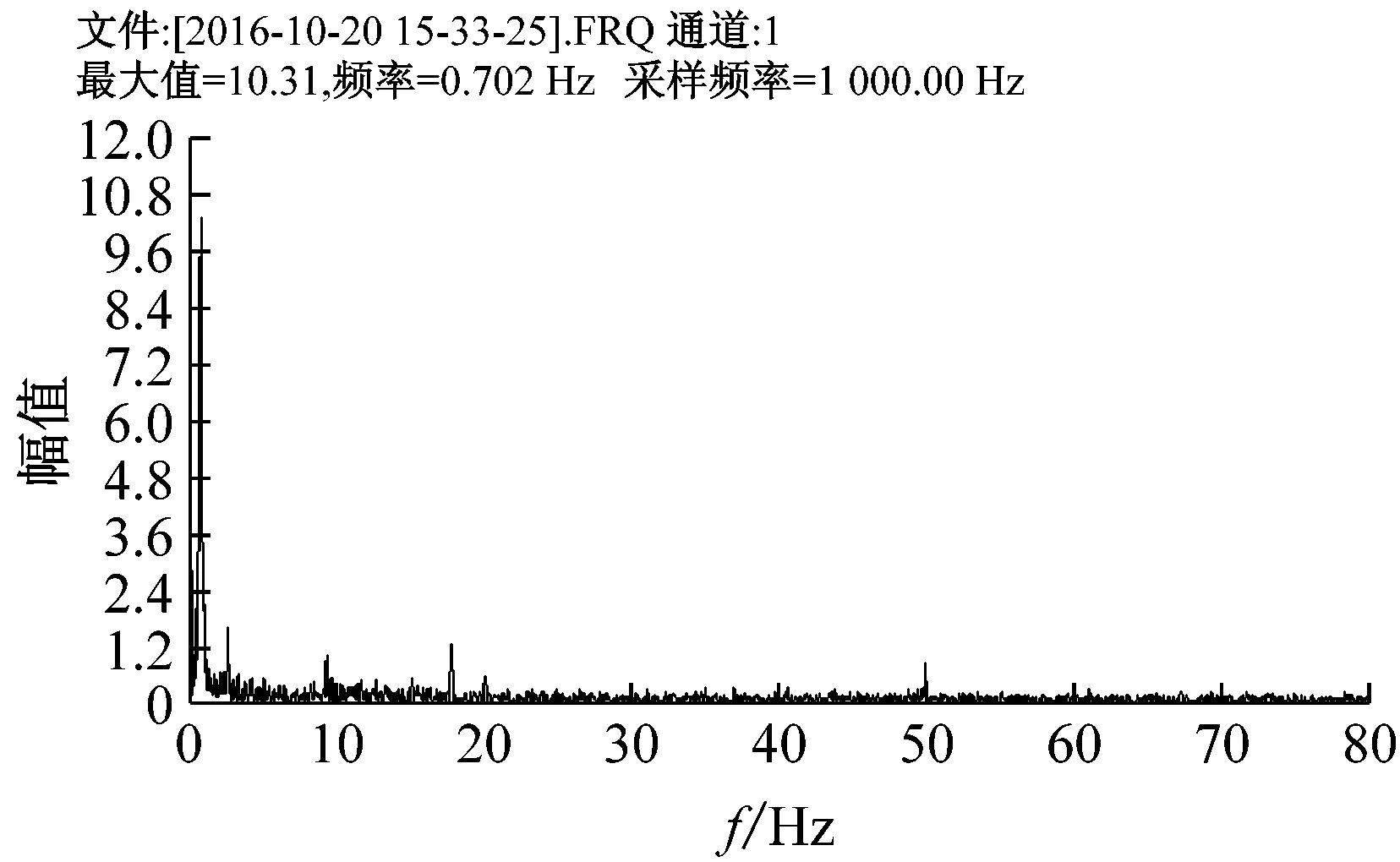
(b) 3.5D导程立管

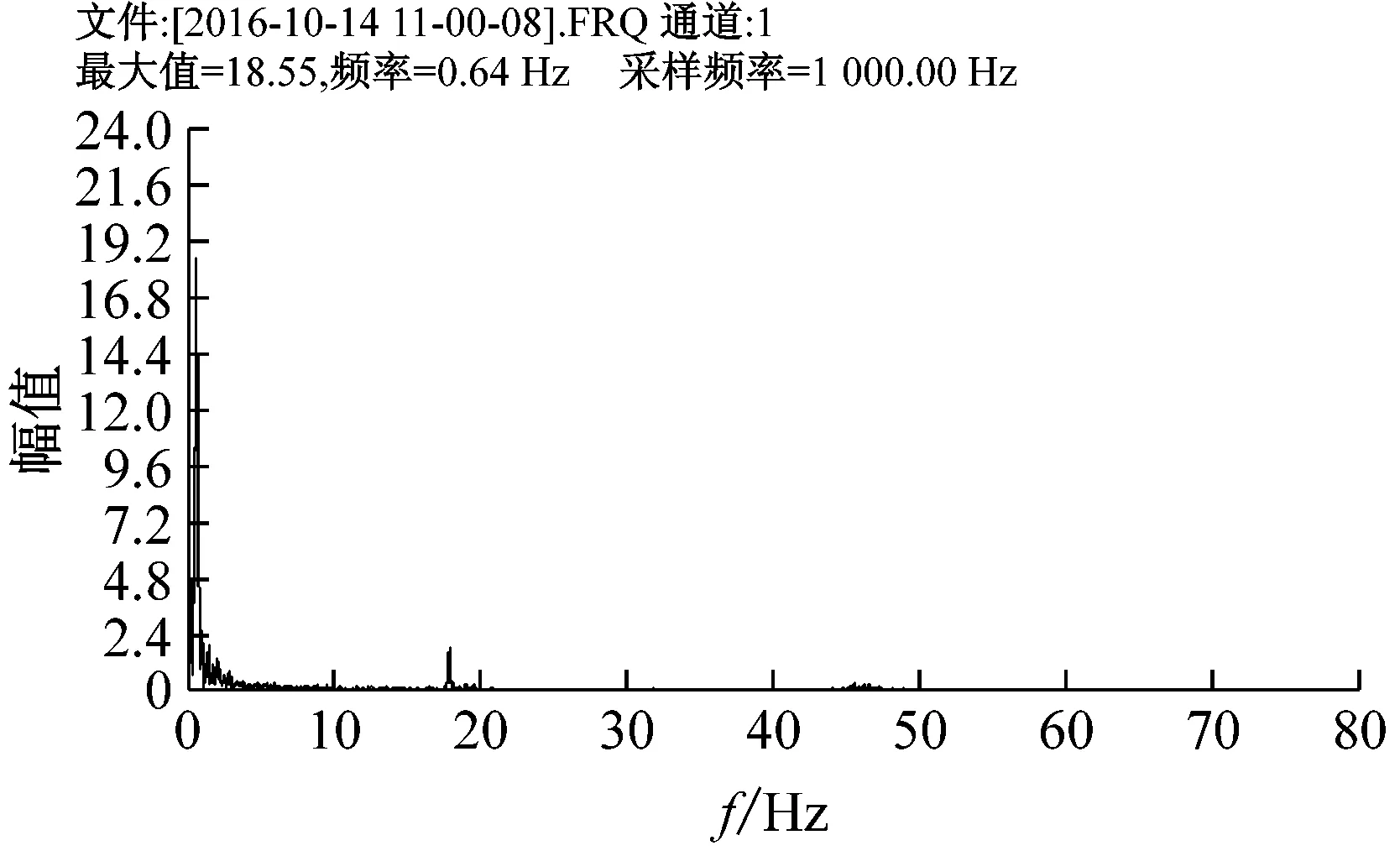
(c) 6D导程立管

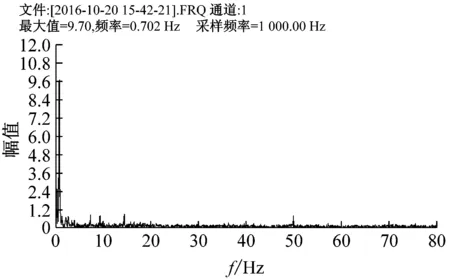
(d) 9D导程立管图8 Re=1 500时的频谱分析图Fig.8 Re=1 500, spectrum analysis of vortex-induced vibration

Re=1 500时，光滑立管、3.5D导程立管、6D导程立管、9D导程立管的St数分别为0.21、0.19、0.17、0.19，由于带螺旋侧板立管的水动力直径难以计算，此处计算St数所采用的直径均为管直径，这一定程度上导致了带螺旋侧板立管计算所得St数的减小。

图9给出了4组立管模型的St数随雷诺数变化的情况。从图中可以看出，光滑立管的St数几乎在各雷诺数情况下都比其他3组带螺旋侧板立管的要大，而且在雷诺数200以前，St数呈递增形式，在雷诺数200以后，基本在0.21附近，这与现有光滑圆柱体的研究结果一致。3组带螺旋侧板立管的St数随雷诺数变化并不表现得与光滑立管非常一致，从整体上看，雷诺数200以前的这3组立管的St数基本在0.17附近，雷诺数200以后在0.19附近，而且这3组立管的St数随雷诺数变化曲线也并不存在明显的大小关系，是3条相互交叉的曲线，可以认为立管的螺旋侧板导程变化对St数有影响，但是与St数变化并无明显规律性关系。

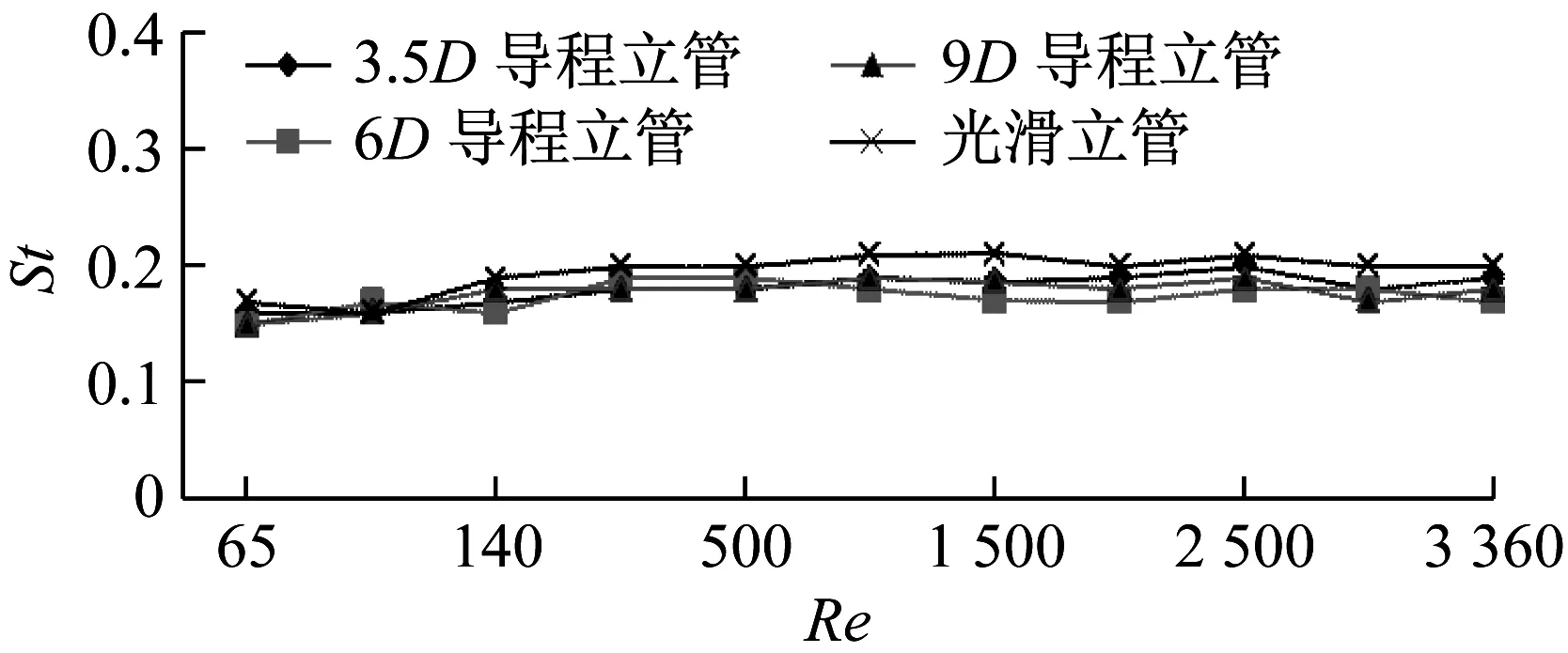
图9 4组立管的St数变化Fig.9 Strouhal number of the four models

3 结 论

本文就3组不同螺旋侧板导程的立管和一组光滑立管在不同雷诺数下进行了两向涡激振动对比试验，可以得出以下结论：

(1)通过对立管两向涡激振动响应时程的分析发现，4组立管横流向与顺流向振动的相位差均为90°，可见立管的振动轨迹为椭圆形。有无螺旋侧板对立管的振动轨迹影响较大，而螺旋侧板导程的变化对立管的振动轨迹影响很小。

(2)通过对比4组立管模型的两向涡激振动应变响应发现，螺旋侧板的应用可以大幅度减小立管的横流向振动响应，减小幅度可达70%左右，但立管的顺流向振动响应有一定程度的增加，在很多情况下带侧板立管的顺流向振动响应甚至超过了横流向的振动响应，这是目前涡激振动研究中比较少见的。其中9倍管径导程的螺旋侧板对立管的涡激振动抑制效果最佳，配置该侧板立管的两向涡激振动响应较其他两组带侧板立管的两向振动响应都要小。

(3)通过对尾流涡旋泄放的示踪显示，观察到了光滑立管明显的2S泄放模式，并展示了螺旋侧板对流场的扰乱作用，试验的尾流显示效果达到了数值模拟水平。同带螺旋侧板的3组立管相比，光滑立管的斯托哈尔数在各雷诺数情况下普遍要大一些，雷诺数200以后，光滑立管和带侧板立管的斯托哈尔数分别在0.21和0.19附近。

本文对带螺旋侧板立管的两向涡激振动特性进行了试验研究，揭示了螺旋侧板抑制涡激振动的机理以及抑制效果，对工程应用有重要参考价值。本文的研究内容未对螺旋侧板的厚度，高度等参数以及模型两端的边界条件进行讨论，在下一步研究工作中可以对这些设计参数进行比较分析，必要时还可以引入数值模拟。