深孔台阶爆破近区振动信号趋势项去除方法*

韩 亮，刘殿书，辛崇伟，梁书锋，凌天龙，武 宇，李 晨

(1.华北科技学院安全工程学院，北京 101601; 2.中国矿业大学(北京)力学与建筑工程学院，北京 100083; 3.北京科技大学土木与环境工程学院，北京 100083)

振动测试过程中，由于周边环境及系统自身而导致的振动波形偏离基线中心的现象，称为信号趋势项。在深孔台阶爆破震动观测中，近区信号受趋势项的影响比远区更大。受趋势项影响，波形最大峰值将发生变化，频谱分析的精度降低，同时也会对信号的积分变换造成一定的影响。

近年来，有不少学者对趋势项的消除方法进行了研究[1-2]，其中，小波法和经验模态分解(empirical mode decomposition, EMD)法应用于非平稳信号处理的案例较多[3-4]。二者区别在于，小波法需针对信号特征事先选择小波基函数及分解层数，分解得到的低频系数可能与趋势项频带差距较大，分解过程对操作者的先验知识水平要求较高；而EMD法为自适应分解，对先验知识水平要求较低，但EMD法在分解过程中，会受到端点震荡和模态混叠效应的影响，最重要的是，目前尚无依据确定哪个固有模态函数(intrinsic mode function, IMF)分量为趋势项的主要组成部分。

基于此，本文中拟采用集合经验模态分解(ensemble empirical mode decomposition, EEMD)并结合小波阈值去噪方法，辅以人工判别及自相关分析手段，探索并建立适用于爆破近区的振动信号趋势项去除方法。

1 趋势项去除方法

1.1 基于人工判别的EEMD趋势项去除方法

1.1.1EEMD方法对EMD方法的改进[5]

EEMD方法较EMD方法的改进主要在于：在进行EMD分解时，加入高斯白噪声，原信号经多次添加噪声序列，并多次分解后，对同一尺度下各IMF分量求和，可得到各IMF分量的“集体”。由于加入的i次噪声是不相关随机序列，其统计均值为零，因此，对各IMF分量整体平均后，加入的i次噪声可近似相互抵消。

1.1.2EEMD方法的分解步骤

(1)添加标准白噪声信号wi(t)至原信号x(t)，二者等长。

xi(t)=x(t)+wi(t)i=1,2…,n

(1)

式中：i为加入噪声的次数，xi(t)为原信号x(t)加入i次噪声后的信号。

(2)对xi(t)进行EMD自适应分解，得到相应的各IMF分量，记为cij(t)，余项为ri(t)，cij(t)为第i次加入白噪声后分解得到的第j个IMF，j=1,2…,k，其中k为分解尺度。

(3)对各IMF分量进行总体平均，即得真实的IMF分量:

(2)

1.1.3人工判别

针对分解得到的各IMF分量，目前尚缺少明确的判别准则来识别哪一个分量为趋势项有效组成部分，趋势项的去除存在一定的盲目性。通过对深孔台阶爆破近区大量实测振动信号的分析，总结出趋势项产生的原因，结合现场振动测试系统的物理指标，可建立人工判别准则。

(1)近区爆破振动的特点是瞬时输入能量大、持时短、振幅波动大。传感器在较大脉冲的作用下，受内部惯性原件和电路部分的输出限制，测量指标很难保持线性输出；

(2)目前广泛使用的的爆破测振仪，其可测频率的最低值一般为5 Hz。现场观测得到的爆破信号，低于5 Hz的部分将很难保持线性输出，因此可视为低频干扰。

1.2 基于自相关分析的小波阈值去噪

利用EEMD方法对原始信号分解并消除趋势项分量后，引入的高斯白噪声将导致重构信号的信噪比明显下降。此时，可通过小波阈值法对保留的IMF分量进行去噪。为了有效甄别噪声分量，可借助自相关函数的特性，对保留IMF分量进行辅助判别，并对判别得到的具有噪声特征的分量进行去噪处理，最后，将所有IMF分量重构，整个去噪过程结束。

1.2.1自相关分析

随机变量在时间域的相互依赖关系可以用自相关函数来表示，如下所示：

(3)

式中：x(t)代表某一随机过程，N为采样点个数，t1和t2为不同时刻。

对于高斯白噪声，其自相关函数在图像上通常具备如下特点：最大值集中在坐标零点，其余各点近似为零。

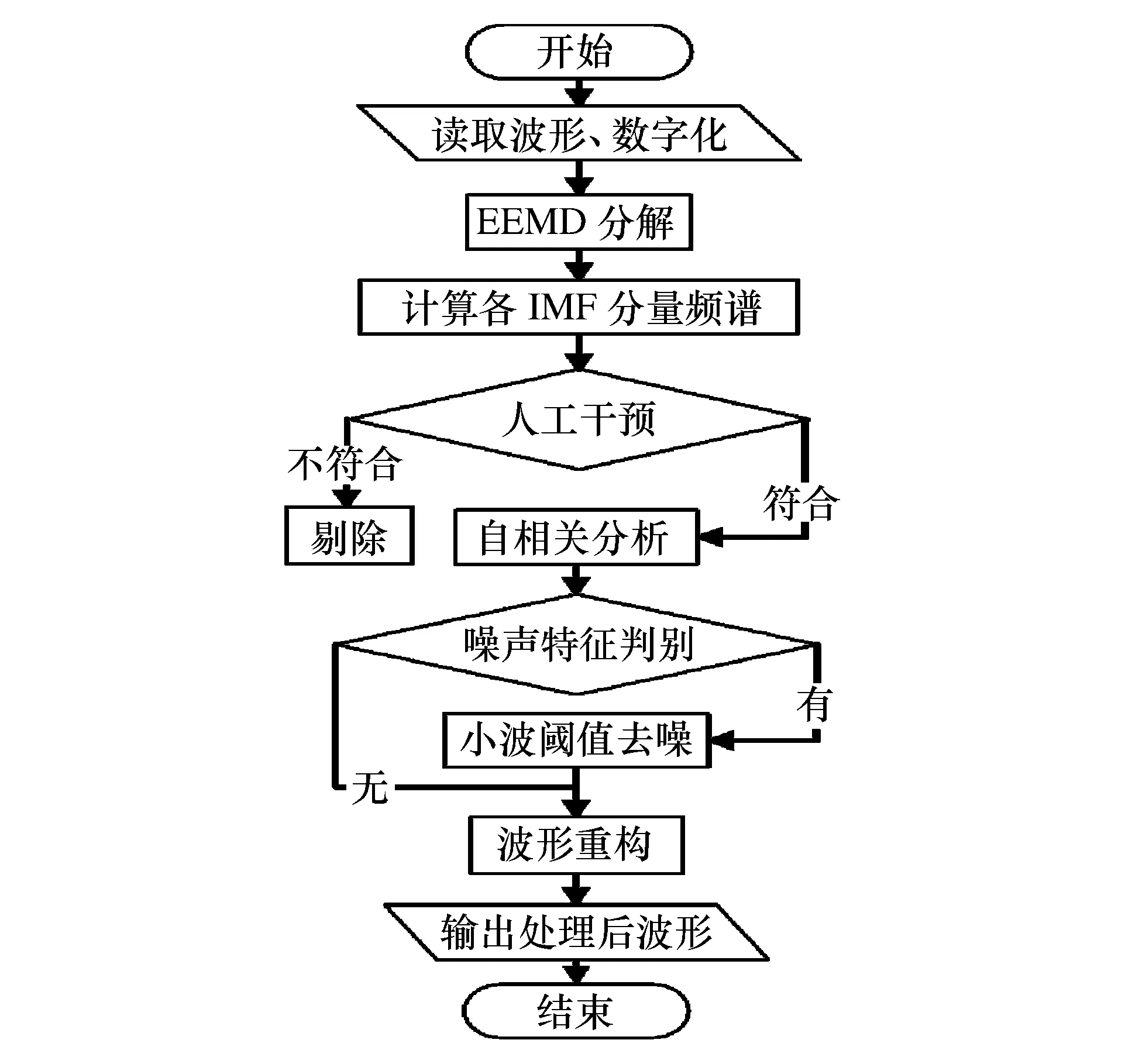
图1 趋势项去除流程Fig.1 Removal process of trend

1.2.2小波阈值去噪

小波阈值去噪是通过比较小波系数与设定阈值的大小，以此来判断小波系数主要是由信号还是噪声引起。去噪前首先需要确定阈值门限并选择合理的去噪方法。阈值门限的选取规则主要有固定阈值门限准则、无偏风险估计准则、混合阈值门限准则以及极大极小阈值门限准则；去噪方法主要有为软、硬阈值法。将去噪后的小波系数重构，即得到了去噪后的信号。

1.3 趋势项去除流程

根据上述分析，整理得到了深孔台阶爆破近区振动信号的趋势项去除方法，通过Matlab平台可编程对实测波形进行批量化处理，如图1所示。

2 实例分析

2.1 测试条件

选取现场某次垂向振动信号，利用前述方法对实测信号进行趋势项去除，并对重构信号进行评价。测试的条件见表1。

表1 信号测试条件Table 1 Conditions of the test signal

2.2 趋势项去除

2.2.1EEMD方法分解

初始设置白噪声标准差为0.1，集成次数100。分解得到14个IMF分量及1个余量r，如图2所示。

图2 EEMD方法分解结果Fig.2 Decomposition results by EEMD method

从图中不难看出，EEMD方法分解得到的各IMF分量，端点振荡效应及模态混叠效应已基本消除。

2.2.2IMF分量尺度排序

利用FFT变换，可以得到各IMF分量的尺度信息。按照由大到小的顺序，各IMF分量的主频，如表2所示。由于趋势项是低频干扰，为简化显示范围，可略去高频分量IMF1～IMF4，仅在频谱曲线图中显示IMF5～IMF15分量，如图3所示。

表2 各IMF分量主频Table 2 Dominant frequency of each IMF component

图3 IMF分量频谱图Fig.3 Frequency spectra of IMF component

2.2.3人工干预判别

由图5可以看出，IMF5～IMF8频段较高，频带较宽；IMF9～IMF14频段较低，频带较窄。由表2中各IMF分量的主频值可知，IMF9～IMF14分量主要集中在0～5 Hz频带，已明显超出爆破测振仪的有效监测范围，上述分量将引起信号趋势项的产生。因此，需将IMF9～IMF14分量去除。

2.2.4趋势项去除后剩余分量重构

对保留的IMF1～IMF8分量重构，如图4～5所示。从图中可以看出，波形重新回到基线中心，主频也由低频缓慢过渡到合理区间，主频幅值突高的情况消失。

图4 原始波形与重构波形Fig.4 Original and reconstruction waveforms

图5 原始波形与重构波形频谱Fig.5 Spectra of original and reconstruction waveforms

2.2.5自相关分析

对保留的IMF1～IMF8分量进行自相关分析，如图6所示。由图中可以看出，8个IMF分量中，IMF1～IMF3分量的自相关函数符合高斯白噪声的特征，因此，主要对IMF1～IMF3分量进行小波阈值去噪。

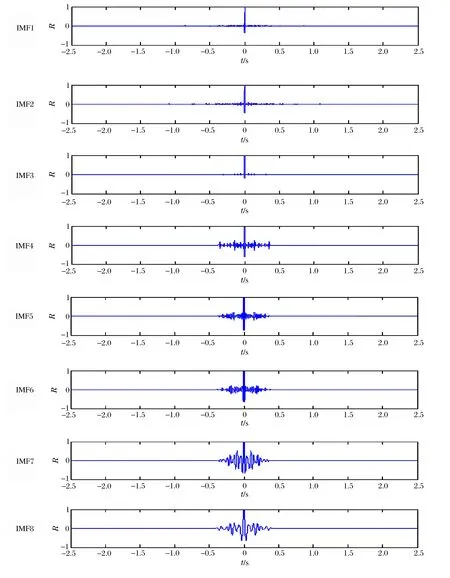
图6 IMF分量自相关函数图Fig.6 Autocorrelation function graphs of IMF components

2.2.6小波阈值去噪

阈值函数确定方法较多[6]。本文中阈值门限准则采用heursure函数，去噪方法采用软阈值函数。

2.2.7去噪后剩余分量重构

IMF1～IMF3分量去噪结束后，将其与其余IMF分量一并进行重构，即可得到最终爆破振动信号，如图7所示。从图中可以看出，去噪后波形的信噪比得到一定提升，滤波效果显著。

图7 小波阈值去噪前后波形对比Fig.7 Contrast of wavelet thresholds before and after denoising

3 结 论

(1)深孔台阶爆破条件下，爆破近区振动信号产生趋势项的原因为瞬时大能量输入引起的非线性失真，在此基础上以测试仪器有效监测范围作为识别趋势项组成部分的判别准则。

(2)借助EEMD方法及小波分解，提出一种基于各IMF分量频带指标，辅以人工判别的趋势项去除方法，以及利用自相关分析识别噪声特征的小波阈值去噪方法，并通过实例验证了方法的有效性。