三模块IPOS高压直流电源系统的稳定性研究∗

吴 帅 李进军李 强

（1.海军大连舰艇学院学员五大队 大连 116018）（2.海军大连舰艇学院导弹与舰炮系 大连 116018）

1 引言

近年来，随着高压直流电源在大功率武器装备上越来越广泛的应用，对采用多模块输入并联输出串联（IPOS）的方式以满足高电压输出的要求也随之提高［1～7］。输出串联的串联变换器提高了输出电压，但带来了各电源模块输出电压不均的问题，电压不均导致纹波过大，部分模块所受应力过大，降低了电源寿命［8～9］。这些应力分布不均会直接导致各模块的工作状态不稳定，若电源系统工作不稳定，负载功率将失去平衡且在逐渐恶化的过程中将导致整个电源系统的瘫痪，继而使武器装备系统瘫痪，不能正常工作，将极大地影响战斗能力，在战时甚至会影响战争的胜败。本文基于三模块输入并联输出串联系统（IPOS）的小信号模型，对三模块IPOS高压直流电源系统进行了稳定性分析，验证了基于阻抗的稳定性分析方法的可行性，为研究多模块串联高压直流电源的系统稳定性提供了理论依据［10～12］。

2 三模块的小信号模型

由《三模块IPOS高压直流电源系统的小信号建模》一文中得到三模块的电路系统的控制框图，如图1。

由三模块控制系统的控制图得系统闭环传递函数为

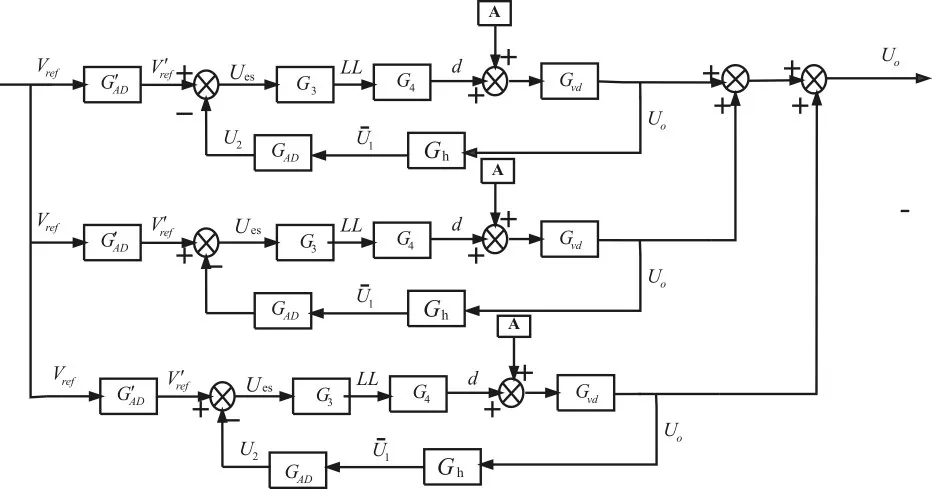
图1 三模块系统控制框图

则系统的闭环系统的开环传递函数为

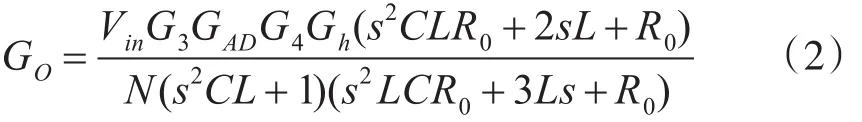
3 三模块IPOS系统的稳定性分析

按并联输入电压为220V，串联输出目标电压为3000V，输出电流1A。则有 N=0.2，R=1000，

N为变压器变比；Gud为与之间的传递函数；Gh为霍尔电压传感器；GAD为AD转换器；A为额定占空比；G3，G4为DSP转换，近似于比例环节。

代入参数（本文下面所用参数均为以上参数）到系统的开环传递函数为

3.1 劳斯判据判断稳定性

由系统的开环传递函数得系统闭环特征方程为

列写劳斯表：

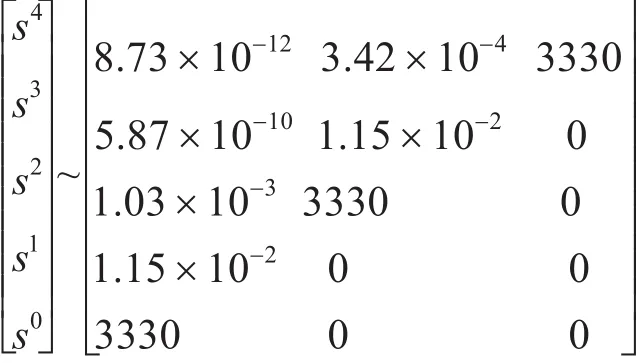
由劳斯判据得，第一列元素全为正，系统稳定。

3.2 Bode图判断系统稳定性

对所推导的三模块的开环传递函数式（3），在Matlab环境下进行编程仿真。

所得的Bode图如图2所示。

图2 系统Bode图

图中相角裕度 pm=4.37°，幅值裕度Gm=Inf，截止频率Wcp=4.5320e+03，由系统的稳定性条pm＞0，Gm＞1，可以看出系统稳定，稳定裕度较低，稳定性能不高。

3.3 基于阻抗的稳定性分析方法

3.3.1 阻抗分析系统稳定性原理

1）电源系统的模型分析

电源模块的时域模型是将电源系统分成了两个模块，其中Zo是输出负载，Zi是输入负载。电源系统时域模型框图如图3所示。

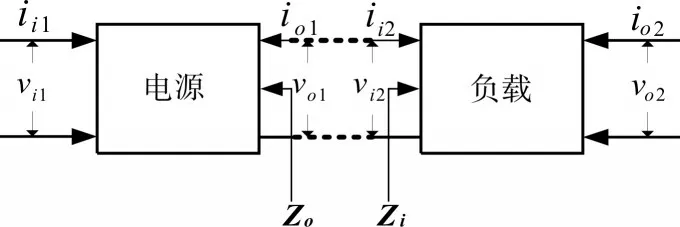
图3 电源系统的时域模型

框图中的次环路增益Zo∕Zi可用图4所示的次环路增益模型框图进行详细描述。

由图4可以得出源模块和负载模块的输入输出电压电流的关系：

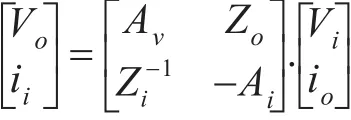
得：

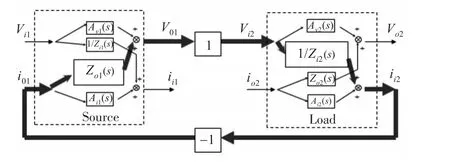
图4 次环路增益模型

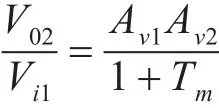
其中：

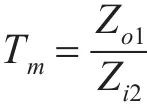
2）稳定性判断方法

3.3.2 三模块系统稳定性分析

1）小信号建模求负载阻抗

图5 三模块小信号电路

由变压器二次侧建立小信号：

各个模块的输出电压的关系有：

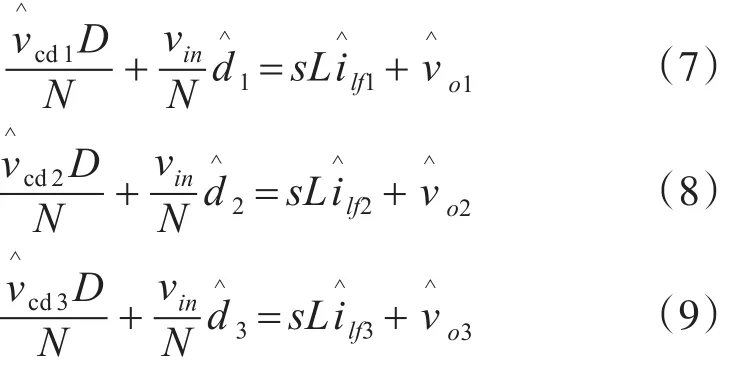
变压器源负载侧的电流关系有：

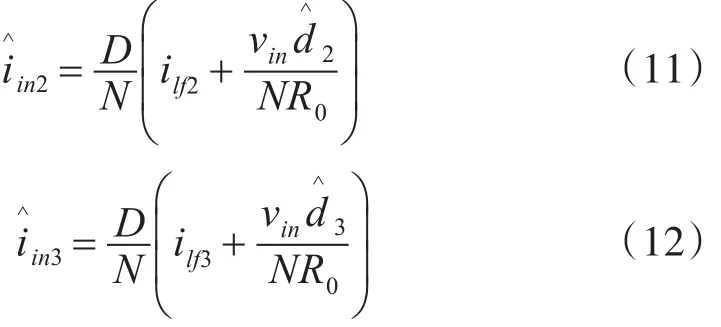
系统的控制图如下：

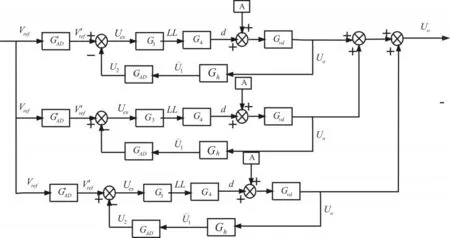
图6 三模块系统控制图

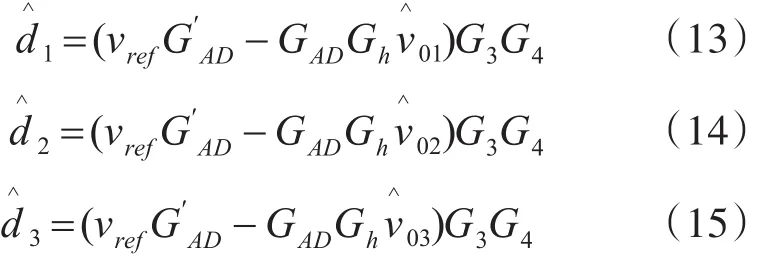
由式（17）～式（18）得：

由式（16）～（21）得三模块的负载输出端等效阻抗为

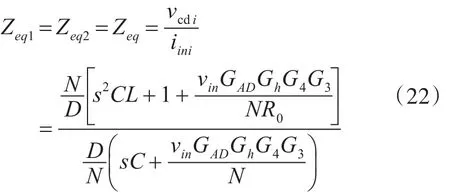
2）三模块的等效模型

将三个模块等效成源模块和负载模块两部分，源模块为一个单模块，负载模块是另外两个模块的并联然后加上原来的负载R。三模块源负载等效模型如图7所示。

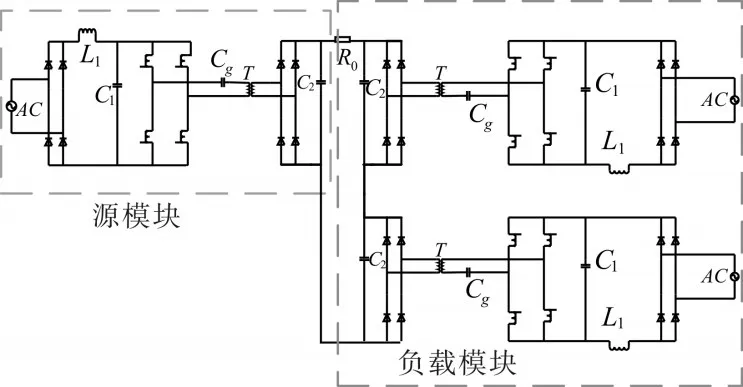
图7 三模块源负载等效模型

3）稳定性判定

Zo1为源模块的输出阻抗，Zin为负载模块的输入阻抗。

由式（23）～式（24）得源负载模块阻抗比Tm：

代入各电器元件参数，得：

由式（26）在Matlab环境下仿真得到奈式图如图8所示。

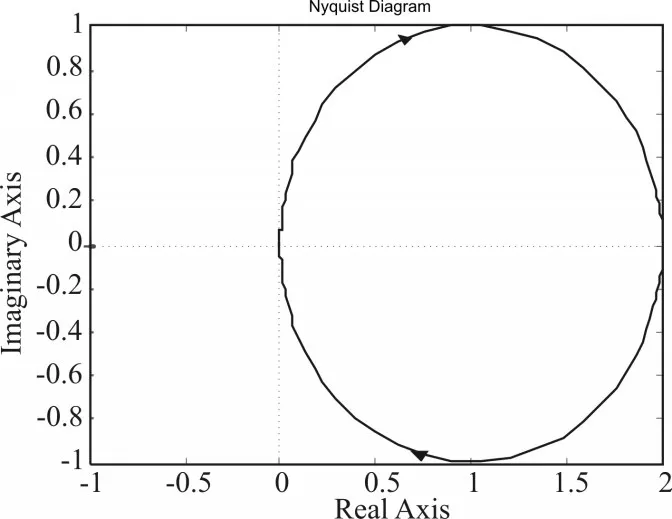
图8 阻抗比Tm的奈式图

根据奈奎斯特判据，级联电源系统稳定的充分必要条件是：在复平面上，Tm不包围（-1，j0），而由仿真结果可以看出，奈氏曲线未环绕（-1，0j），所以系统稳定。

3.4 三模块的Simulink仿真

三模块的Simulink仿真模型如图9。

图9 三模块Simulink仿真模型

仿真模型输入的参考电压vinf为1000V，每个模块的期望的输出电压为1000V，输出的总电压为3000V。仿真结果与细节如图10、11所示。

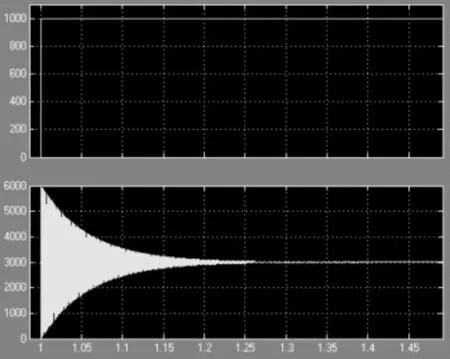
图10 三模块Simulink仿真图

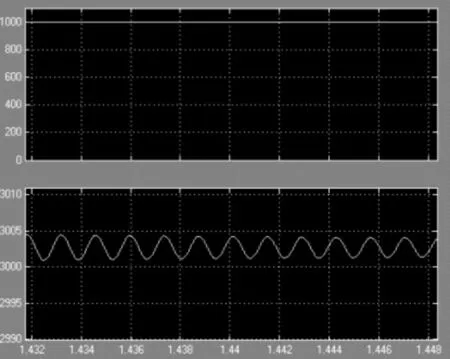
图11 Simulink仿真仿真细节

由图10～11可以得到，系统的输出在0.25s时候达到稳定，在达到稳定前，纹波较大，超调大，电源输出达到稳定后满足期望的输出值。印证了理论推导的正确性。

4 结语

本文对三模块IPOS高压直流电源系统进行了稳定性分析研究，通过劳斯判据、画伯德图及阻抗稳定性判据的系统稳定性判别方法对三模块进行了理论的验证分析，得出了三模块系统稳定。从计算的简便性可以看出，基于阻抗的稳定性判据思路简单，计算量少。本文只是通过理论的推导对三模块进行了稳定性判断。验证了基于阻抗判断系统稳定性的方法的可行性。为通过实验的方法进行测量提供了理论依据。对于三模块的模型的建立和理论的推导就已经如此麻烦，那么，对于多模块的IPOS系统的稳定性判断就更麻烦了，计算量异常庞大。很明显，用理论推导的方法对系统稳定性进行分析已经不再实用。基于阻抗的稳定性分析方法为解决这个问题提供了可行性的办法，只用测量源负载模块的阻抗，便能判断出系统的稳定性，省去了大量的计算量，提高了工作效率。