界面状态对椭圆钢管混凝土轴压短柱影响分析

程 高，张正琦，刘永健，孟俊苗

1)长安大学公路学院，陕西西安 710064；2)陕西省公路桥梁与隧道重点实验室，陕西西安 710064；3)旧桥检测与加固技术交通行业重点实验室(西安)，陕西西安 710064

椭圆钢管混凝土具有力学性能好、造型优美等特点，在工程中的应用逐渐扩大. 椭圆钢管混凝土轴压承载力高，适合用作以轴心受压为主的桥梁构件，如桥墩、拱肋和桁架弦杆[1]. 椭圆钢管混凝土具有良好的流体力学性能，可有效减少水流和风对结构的冲击作用. 其绕两对称轴的惯性矩不同，可通过调整截面尺寸及长短轴比最大限度提高构件的抗弯承载力和刚度.

钢管与混凝土界面状态易受混凝土收缩徐变、温度及受荷方式等影响发生明显改变，从而影响钢管混凝土柱及节点的工作性能. 刘爱荣等[2-3]进行了30个方、圆钢管混凝土界面推出试验，指出方、圆形钢管混凝土界面黏结-滑移曲线具有相似的变化规律，在达到黏结强度之前基本呈线性关系，达到黏结强度后保持不变，且两者剪切模量接近. 圆钢管混凝土界面抗剪黏结强度明显大于方钢管混凝土界面抗剪黏结强度，界面黏结强度受混凝土强度的影响不明显，随混凝土龄期的增大而略有增大，随钢管长径比的增大而增大，随钢管径厚比(宽厚比)的增大而减小[4]. 在此基础上，刘永健等[5]提出方、圆钢管混凝土界面抗剪黏结-滑移本构关系. 姜绍飞等[6]提出，钢管混凝土界面黏结强度从方形、八边形到圆形呈增大趋势，机械振捣方式下黏结强度明显比人工振捣方式下的要大. 仵建斌[7]进行了14个方钢管混凝土构件推出试验，将界面黏结滑移过程分为无滑移阶段、滑移阶段、破坏阶段、下降阶段和水平残余阶段，并给出了相应的黏结强度计算公式. 蔡绍怀[8]进行了11个不同轴压比的界面黏结破坏试验，指出轴压比对黏结强度的影响显著，随偏心率和轴压比增大黏结强度均呈增加趋势.

钢管混凝土轴压构件在工程应用中可能出现的典型受荷模式，主要有钢管和混凝土共同受力、仅混凝土受力及仅钢管受力等. 不同受荷模式下钢管混凝土轴压短柱的破坏模式和工作性能存在较大区别. 而现有研究多集中在钢管和混凝土共同受力这一模式. 韩林海等[9-10]对比了钢管内是否进行涂油处理对轴压短柱承载力的影响，指出界面脱黏与否对圆、椭圆钢管混凝土构件的承载力影响不明显. 于学增[11]建立无黏结、完全黏结及半黏结状态下方钢管混凝土轴压短柱有限元模型，提出黏结状态对短柱轴心受压承载力、刚度和破坏模式的影响不大，其差异基本在相同试件的误差范围内. 王玉银等[12]开展了不同受荷模式下圆钢管混凝土力学性能的有限元分析，指出钢管和混凝土共同受力模式下黏结强度对轴压短柱的力学性能没有影响，仅混凝土受力模式下无黏结强度时，钢管对管内混凝土的约束作用增强，构件极限承载力增大，但刚度减小. LIU等[13]进行了仅混凝土受荷模式下圆钢管约束混凝土轴压试验，指出界面摩擦系数越小，钢管纵向应力就越小，横向应力越大，钢管对混凝土的约束作用增强. 可见，考虑不同受荷方式时，界面状态对构件的力学性能影响规律不一致. 为此，本研究针对椭圆钢管混凝土这种新型构件，引入受荷模式，分析界面状态对轴压短柱力学性能的影响，为椭圆钢管混凝土的推广应用提供技术支撑.

1 模型参数设计

钢-混界面状态可分为完全黏结、有黏结滑移和完全脱黏等3种情况. 完全黏结的界面状态是一种主要用于钢管混凝土结构分析的假定，便于数值模拟和理论推导分析. 本研究完全黏结参数采用线弹性的黏结-滑移本构关系，且剪切模量较高，以保证钢管与混凝土轴压过程中界面不分离. 有黏结滑移状态是钢管混凝土界面的正常工作状态，直接使用文献[5]中黏结-滑移本构关系. 完全脱黏状态是钢管混凝土界面易受施工条件和工作环境影响而出现的一种病害状态. 以上3种界面状态反映了钢管混凝土可能出现的典型界面工作状态. 界面黏结滑移的本构关系如图1[5]. 其中，E0为界面法向抗压模量，取决于钢管的面外抗弯刚度；E2为界面黏结滑移剪切模量，文献[5]取165 MPa；E1为完全黏结滑移剪切模量，文献[5]在试验基础上，扩大100倍，取16.5 GPa，以保证钢管与混凝土界面始终保持黏结；E3为脱黏时界面黏结滑移剪切模量，取为0.

图1 界面黏结滑移本构关系[5]Fig.1 Bond slip constitutive relation[5]

图2 受荷模式Fig.2 Force exerting modes

有限元分析模型的参数设计，是在文献[10]椭圆钢管混凝土轴压短柱试件的基础上得到材料的力学指标，并增加了受荷方式和界面状态参数，共有3组9个试件，所有试件的几何尺寸均一致，具体为2b×2a×t=150 mm×75 mm×4 mm，L=300 mm. 其中，b为椭圆钢管半长轴长；a为椭圆钢管半短轴长；t为椭圆钢管壁厚；L为椭圆钢管混凝土柱的长度. 按照受荷方式分为3组试验(图2). 混凝土和钢材分别选用C30和Q235，ET-A代表钢管混凝土共同受力组，ET-B代表仅混凝土受力组，ET-C代表仅钢管受力组，组内试验依据界面状态分为3个试件，以编号序列01、02、03分别表示完全脱黏、有黏结滑移和完全黏结3种钢混界面黏结状态.例如，ET-A-01代表钢管和共同受力，钢混界面完全脱黏状态下的试件. 模型的参数设计可分析不同受荷方式下界面状态对椭圆钢管混凝土轴压短柱力学性能的影响.

2 有限元模型建立

有限元模型考虑了材料非线性、几何非线性和接触非线性.

2.1 钢材和混凝土本构关系

钢材的应力-应变关系曲线采用二折线的弹塑性曲线，钢材弹性阶段的弹性模量Es和泊松比υs分别取2.06×105MPa和0.283[14]，塑性段弹性模量为0.01Es. 混凝土泊松比υc取0.2，混凝土轴心抗压强度及弹性模量取值按《混凝土结构设计规范》GB50010—2010[15]计算. 混凝土本构关系采用ABAQUS有限元软件中的混凝土塑性损伤模型，混凝土单轴受压、单轴受拉模型采用《混凝土结构设计规范》GB50010—2010[15]中混凝土的应力-应变关系，混凝土受压损伤、受拉损伤模型采用《混凝土结构设计规范》GB50010—2010[15]中混凝土的损伤因子-应变关系.

2.2 单元类型选取与模型网格划分

基于ABAQUS有限元软件，钢管采用S4四节点完全积分的壳单元，混凝土采用C3D8八结点线性六面体单元模拟，加载板采用刚性体单元模拟. 模型网格划分采用最小化网格过渡的扫描技术[16]，如图3所示.

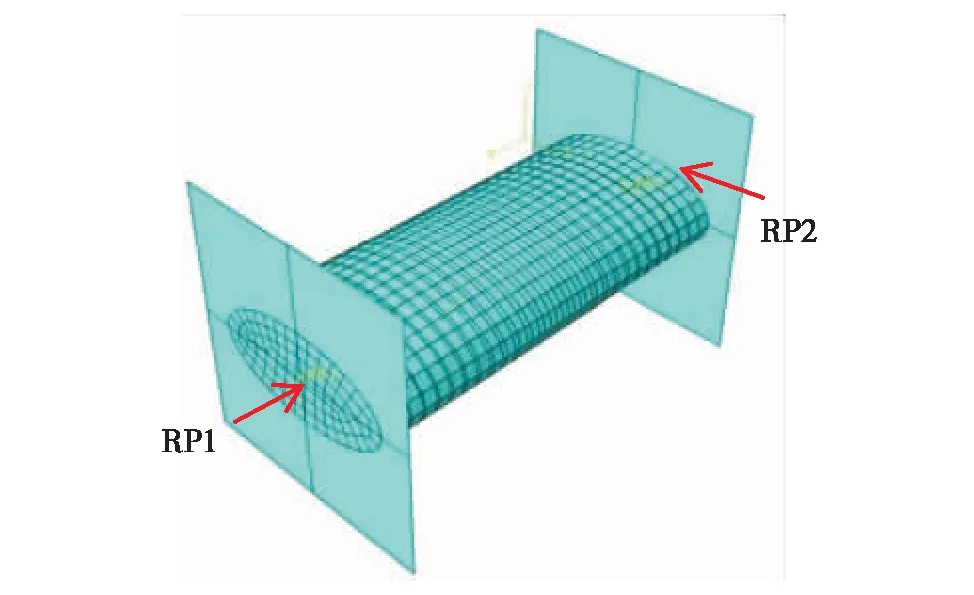
图3 网格划分[16]Fig.3 (Color online) Mesh generation[16]

2.3 界面接触、模型边界及荷载条件模拟

钢-混界面接触模型由钢与混凝土界面的法向接触和切向黏结滑移构成，刚度较大的混凝土作为主面，钢管作为从面. 对于有黏结滑移和完全黏结等界面状态，钢管与混凝土界面法向接触采用ABAQUS中黏性接触模型，接触界面法向和切向行为均采用图1中黏结滑移本构关系. 对于脱黏状态，界面法向接触采用“硬”接触，接触面传递界面压力p， 界面切向接触采用“库仑摩擦”模型，界面摩擦系数取0[17].

在加载板中心设置参考点RP，参考点与加载板采用耦合连接，约束参考点RP1的X、Y和Z方向的平动自由度，约束参考点RP2的X、Y方向的平动自由度，并施加参考点RP2的Z正方向的10 mm位移，参考点位置如图3所示. 改变参考点RP2对应的加载板与椭圆钢管混凝土柱的连接条件，实现不同受荷模式.

2.4 非线性有限元模型的验证

基于上述建模方法，采用文献[10]中椭圆钢管混凝土柱钢材及混凝土力学指标和加载方法，分别建立混凝土标号为C30、C60和C100的有限元模型，并提取其轴向荷载-位移曲线，与文献[10]试验值对比可知，有限元计算值与试验值总体吻合较好，验证了本研究有限元模型的可靠性.

3 结果分析

3.1 界面法向应力分布

图4至图6分别为模式A、B和C下界面法向应力随极限荷载倍数的变化曲线. 由于椭圆钢管混凝土短柱呈中心对称，仅选取1/4截面进行分析，取界面法向压应力为正，拉应力为负.

图4 模式A下界面法向应力变化曲线Fig.4 (Color online) Interfacial normal stress on mode A

由图4可知，在0.5倍的极限荷载前，界面法向应力较小，材料的泊松比影响着界面法向应力分布；由于钢的泊松比大于混凝土的泊松比，轴压过程中钢管横向变形较管内混凝土大，使得界面法向以拉应力为主，形成钢管拉伸混凝土状态. 超过0.5倍的极限荷载后，界面法向应力沿椭圆圆周方向呈现出不均匀分布，长轴顶点处界面法向压应力最大，离长轴顶点越远压应力值越小，最远到短轴顶点处压应力最小. 管内混凝土刚度退化加剧，横向变形增大，且变形速度较钢管快，使得界面法向以压应力为主，形成钢管约束混凝土受力状态. 可见，界面完全脱黏推迟了钢管约束混凝土作用，界面法向应力分布不同于有黏结滑移和完全黏结界面状态. 在钢管和混凝土共同受力模式下，有黏结滑移状态和完全黏结状态两者界面法向应力分布基本一致，均随荷载的增加而增大.

图5 模式B下界面法向应力变化曲线Fig.5 (Color online) Interfacial normal stress on mode B

由图5可知，仅混凝土受力模式时完全脱黏和有黏结滑移界面状态下界面法向以压应力为主，且随轴压荷载的增加而增大，构件处于钢管约束混凝土状态. 完全黏结状态下，0.8倍的极限承载前，界面法向以拉应力为主.拉应力不足0.1 MPa，达到0.8倍的极限荷载后，界面法向应力由拉应力逐渐变为压应力.钢管对混凝土的约束作用较弱，这是由于钢管与混凝土界面始终黏结，荷载沿柱轴向传递一定长度后变为钢管和混凝土共同承担.

图6 模式C下界面法向应力变化曲线Fig.6 (Color online) Interfacial normal stress on mode C

由图6可知，仅钢管受力模式时，完全脱黏、有黏结滑移和完全黏结3种界面状态下，界面法向应力存在本质区别. 完全脱黏状态下，界面法向应力为0；有黏结滑移状态下，界面法向应力以拉应力为主；完全黏结状态下，0.9倍的极限荷载前界面法向应力表均为拉应力，随着荷载的增加，界面法向应力由拉应力转变为压应力.

3.2 钢管和混凝土截面压应力分布

图7和图8给出了短柱达到极限荷载时各界面状态对应的混凝土中截面压应力分布. 由图7可知，钢管和混凝土共同受力模式时3种界面状态下管内混凝土压应力分布情况接近，均表现为压应力峰值出现在椭圆长轴顶点处，离椭圆长轴顶点越远，压应力值越小.

图7 模式A下混凝土截面压应力分布(单位：MPa)Fig.7 (Color online) Compressive stress of concrete section on mode A(unit：MPa)

由图8可知，仅混凝土受力模式时完全脱黏和有黏结滑移状态下混凝土压应力分布情况接近，完全黏结状态下混凝土压应力值较小. 综上，混凝土截面压应力呈“双同心圆”分布，圆心位于长轴顶点处. 仅钢管受力模式时，混凝土截面压应力接近0；椭圆钢管混凝土轴压过程中，钢管截面压应力呈均匀分布；以上情况不再用图形表示.

图8 模式B下混凝土截面压应力分布(单位：MPa)Fig.8 (Color online) Compressive stress of concrete section on mode B(unit：MPa)

根据有限元计算结果，轴压全过程中混凝土截面压应力均呈“双同心圆”分布，圆心位于长轴顶点处，钢管截面压应力呈均匀分布. 为便于掌握钢管和混凝土截面压应力随轴压荷载及压缩量的变化关系，提取了压应力随纵向应变的变化曲线，如图9所示. 其中，Δ为轴向压缩量；Δ/L为短柱的名义纵向应变. 由图9(a)可见，钢管和混凝土共同受力模式时3种界面状态下钢管和混凝土截面压应力随纵向应变规律基本一致. 由图9(b)可知，仅混凝土受力模式时界面状态显著影响钢管和混凝土截面压应力分布，界面黏结作用越强，钢管截面压应力就越大，混凝土截面压应力就越小，这说明钢管分担的轴向荷载随界面黏结作用的增强而增大. 由图9(c)可见，仅钢管受力模式时界面黏结作用越强，钢管截面压应力就越小，混凝土截面压应力就越大，这说明混凝土分担的轴向荷载随界面黏结作用的增强而增大.

图9 截面压应力变化曲线Fig.9 (Color online) Compressive stress curve

图10 荷载-压缩量变化曲线Fig.10 (Color online) Load-compression change curve

3.3 极限承载力

为分析不同受荷模式的椭圆钢管混凝土轴压短柱极限承载力，本研究得到了各试件的荷载-压缩量变化曲线，如图10所示. 极限承载力取为荷载-压缩量曲线的峰值荷载，轴压刚度取为荷载-压缩量曲线弹性段直线的斜率，用0.4倍极限荷载时荷载-压缩量割线模量表示. 由图10(a)可知，钢管和混凝土共同受力模式下，界面状态对构件的极限承载力不明显，进行构件的承载力计算和分析采用钢管与混凝土界面完全黏结这一假定是成立的. 由10(b)可知，仅混凝土受力模式下，界面状态对构件的承载力影响显著，随着界面黏结强度的提高而呈增大趋势. 由图10(c)可知，仅钢管受力模式下，非完全黏结即完全脱黏和有黏结滑移状态下构件的极限承载力接近，但小于完全黏结状态下构件的极限承载力；完全黏结状态下，钢管受到的约束作用增强从而提高了构件的极限承载力.

3.4 轴压刚度

图11给出了不同受荷模式下各界面状态对应的构件轴压刚度. 由图11可知，钢管和混凝土共同受力模式下3种界面状态下构件的轴压刚度基本一致. 仅混凝土受力或仅钢管受力时完全黏结状态下构件轴压刚度显著高于完全脱黏和有黏结滑移界面状态，但仍小于钢管和混凝土共同受力时构件的轴压刚度.

图11 轴压刚度Fig.11 (Color online) Axial compressive stiffness

4 结 论

综上研究可见：

1)仅混凝土受力和仅钢管受力模式下，界面状态显著影响椭圆钢管混凝土轴压短柱的力学性能. 界面黏结作用越强，钢管和混凝土互相帮助分担荷载的能力就越强，构件抵抗变形的能力就越强. 钢管和混凝土共同受力模式下，界面状态对构件的钢管和混凝土截面压应力、极限承载力及轴压刚度几乎无影响.

2)钢管和混凝土共同受力模式时，椭圆钢管混凝土轴压短柱混凝土截面压应力呈“双同心圆”分布，圆心位于长轴顶点处，离长轴顶点越远，压应力越小，短轴顶点处压应力最小. 钢管截面压应力呈均匀分布. 界面完全脱黏推迟了钢管约束混凝土作用，界面法向应力分布不同于有黏结滑移和完全黏结界面状态，但三者的压应力峰值接近.

3)仅混凝土受力时，非完全黏结状态下构件处于钢管约束混凝土状态，界面法向压应力随轴压荷载的增加而增大，混凝土截面压应力分布基本一致，钢管压应力值较小，构件的极限承载力和轴压刚度均小于完全黏结状态下相应的量值.

4)仅钢管受力模式下，非完全黏结状态下界面法向应力值较小，且达到极限荷载前未出现压应力，混凝土截面压应力值较小，构件的轴压刚度显著小于完全黏结状态下对应的量