基于统计感知的大数据系统计算框架
2018-09-26魏丞昊黄哲学何玉林
魏丞昊,黄哲学,何玉林
深圳大学计算机与软件学院大数据技术与应用研究所,广东深圳 518060
大数据分析的重要挑战之一是如何在一定的计算资源条件下、在可接受时间范围内实现大数据的可计算化[1].分而治之是处理大数据计算的主要策略,即通过将大数据划分为若干小数据块文件分布式存储在集群节点上.在对大数据分析时,通过融合所有数据块并行分析结果来达到对全量大数据挖掘和学习的目的[2].Hadoop分布式文件系统(Hadoop distributed file system,HDFS)[3]主要实现大数据的划分存储和数据块文件的管理.Spark采用弹性分布式数据集(resilient distributed datasets, RDD)内存数据结构将大数据分布式读入节点内存中计算,避免了MapReduce[4]反复地读写磁盘,极大地提高了算法的运行效率[5].但当数据量超出集群的最大内存容量时,Spark算法的执行效率将大大降低,甚至无法运行[6-7].因此,内存资源成为Tbyte级以上大数据的深度分析、挖掘和建模的瓶颈.
通过合适数据划分的方法,使得大数据分布式存储的数据块可直接作为全量数据的随机样本来使用,减少了大数据分析与建模对内存的约束.但是,当前的分布式文件系统的数据块文件不能被当作大数据的随机样本使用,因此本研究在图1的Bigdata-α系统中,提出基于随机样本划分的分布式存储模型和基于逼近式的学习框架.
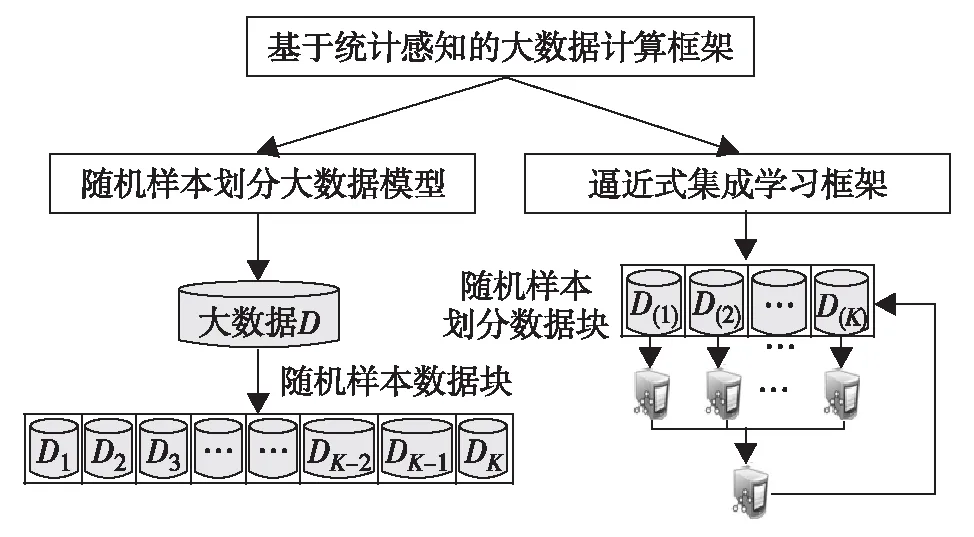
图1 Bigdata-α框架Fig.1 Bigdata-α framework
1 基于随机样本划分的大数据管理
定义1随机样本块. 若D={x1,x2,…,xn}是一个大数据集的样本集合,F(x)是D的分布函数 (sample distribution function).设T完成对D的某种任意划分,则有T={D1,D2, …,DK}, 若T中有
E(Fk(x))=F(x),k=1, 2, …,K
(1)
其中,F(x)为Dk的样本分布函数;E(Fk(x))表示其期望值.满足这样条件下的Dk是D的一个随机样本块.生成随机样本块的算法实现程序的代码请扫描文后二维码.
2 基于逼近式集成学习的大数据分析
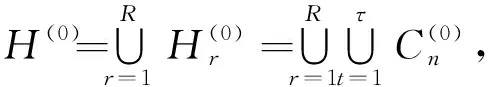
3 实验结果
本研究实验使用包含50个计算节点的集群,每个节点配置为24核CPU、128 Gbyte内存和12.5 Tbyte外存,HDFS最大支持128 Mbyte的切分数据块.图2为基于Spark模拟正态分布的1 Tbyte数据集(1亿条样本记录、每条记录包含100个特征值)被划分成1万个随机样本数据块后相应的样本分布情况.图中显示了随机挑选4个数据块的样本分布与总体样本分布具有一致性,证明了本研究理论的有效性.正是这种一致性保障了通过随机样本数据块所构建的大数据学习模型的无偏性和收敛性.
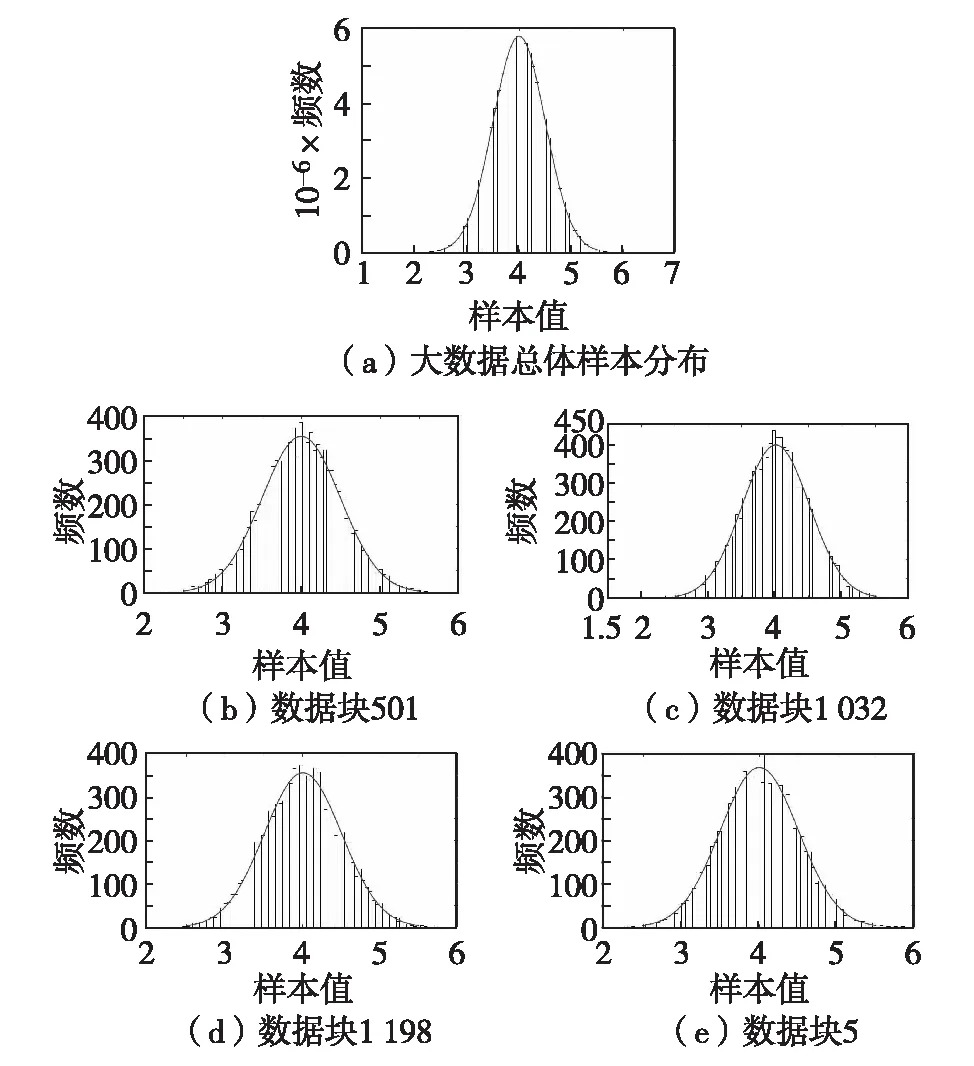
图2 大数据划分后一个样本特征分布Fig.2 Sample distribution after big data partition
图3给出了逼近式集成学习框架利用一致同分布数据块对Higgs数据集分类模型优化的过程.由图3可见,随着数据块的增加,集成学习模型的精度会逐渐收敛,其中虚线为基于大数据总体学习到的单个模型的分类精度.当分析数据量达到整体的15%后,分析精度基本与整体数据分析持平的同时,数据量显示只需使用10%的数据分析结果就可达到使用90%数据量的整体分析精度.
结 语
以大数据“随机样本划分”思想为出发点,提出基于统计感知的Tbyte级大数据系统计算框架Bigdata-α.不同于现有的Hadoop分布式文件系统HDFS,Bigdata-α保证了划分数据块与大数据总体分布的一致性.尽管单个子块存在统计偏差,但是多个子块的集成会逼近原始数据集的统计特性最终实现了对Tbit级大数据的无偏收敛学习.Bigdata-α实现了大数据在计算、统计、优化及应用4方面的统一.Bigdata-α具有处理流式数据的能力,对于与大数据总体分布一致的新增数据,将其直接视为大数据的随机样本数据块;对于分布不一致的新增数据,对其进行随机打乱,重构新的大数据随机样本划分.
致谢:衷心感谢深圳大学张晓亮博士的耐心指导.
