梯度提升随机森林模型及其在日前出清电价预测中的应用

谢晓龙 叶笑冬 董亚明

(上海电气集团股份有限公司中央研究院 上海 200070)

0 引 言

从20世纪90年代末开始，我国就已经开始逐步进行电力体制改革的尝试。

2002年开始电改，其目标包括：实施厂网分开、实行竞价上网等内容。自实施以来，电力行业破除了独家办电的体制束缚，从根本上改变了指令性计划体制和政企不分、厂网不分等问题。但电力行业仍然面临一些亟待解决的问题，包括：交易机制的缺失、市场化定价机制尚未完全形成等问题。因此，国务院于2015年发布《关于进一步深化电力体制改革的若干意见》以及一系列文件，明确指出了深化改革的方向和举措[1]。

电价是电力市场的核心内容，电力市场的参与者以电价进行电力交易和结算，因此，电价的波动直接影响到各个市场参与者的收益。对于发电企业，在竞价市场中，其需要能够准确地预测电价，才能保证提供合理有效的报价，进而实现效益最大化[2]，因此电价的预测是值得研究的问题。

不同的电力交易市场模式中采用了不同的机制，目前采用较多的是统一出清电价的机制。各发电企业分别报价，交易中心按照报价从低到高依次选择，直至发电量与需求电量平衡，最后一个被选中的发电企业报价作为市场出清电价MCP(market clearing price)，最后所有投标获胜的发电企业全部按MCP进行结算[3]。本文以美国PJM(Pennsylvania—New Jersey—Maryland)电力市场中的日前市场为例，研究其日前市场电价的预测问题。日前市场是PJM电能市场的重要子市场，发电商于交易日前一天的截止时间之前提交报价，截止时间过后进行出清，其结果是交易日24个小时的电价。

关于电价预测，研究人员做了大量的探索，采用不同的方法进行预测，包括ARIMA模型[4]、GARCH模型[5]、神经网络模型[6]、小波神经网络[7]、灰色模型[8]、支持向量回归[9]、时间序列分解[10]、决策树[11]等。上述文献大多采用单个全局优化模型，另一种思路是可以采用集成学习模型，即通过结合多个学习机的结果得到更准确的预测结果。集成学习模型中最常用的是随机森林RF(random forest)模型和提升树GBDT(gradient boosting decision tree)模型。集成学习模型一般具有相对较高的预测准确性和模型稳定性。随机森林模型已应用于多个场景，如文本分类[12]、肿瘤诊断[13]等。提升树模型也已成功应用到短期电力负荷预测[14]等领域。

本文在以上两种集成学习模型的基础上，结合二者的优势，提出了一种新的集成学习模型——梯度提升随机森林GBRF(gradient boosting random forest)模型。其能够有效利用随机森林模型稳定性高的优点，并在其基础上，发挥梯度提升算法的优点，进一步提高模型预测的准确性，使得提出的模型优于传统的集成学习模型。

1 梯度提升随机森林模型

1.1 集成学习模型

集成学习模型与传统的全局机器学习模型，如神经网络、支持向量机等不同，其不是学习一个全局模型，而是通过建立一系列机器学习模型，然后将其组合以获得准确性更高、稳定性更好的模型。其中集成学习模型中的各个模型，称为基础学习机。集成学习模型通过一定的集成策略将众多基础学习机集成，最常用的集成策略是Bagging策略[15]和Boosting策略[16]。两种集成学习策略如图1与图2所示。

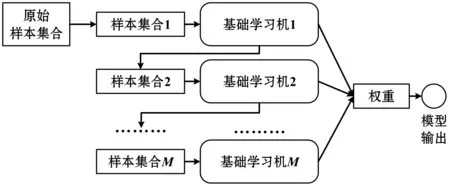
图2 Boosting集成学习策略示意图

如图1所示，Bagging策略采用并行结构，首先使用bootstrap方法进行采样，为不同的基础学习机提供不同的训练样本集合，然后分别训练各个基础学习机，最终将各个结果综合后作为整个Bagging模型的结果。如图2所示，Boosting策略采用串行结构，前一个基础学习机的结果会影响后一个基础学习机的样本，即后续的基础学习机不断修正或提高前面基础学习机的结果。最终将各个基础学习机的结果综合后作为整个Boosting模型的结果。在某些模型中各个基础学习机可能会根据其性能分配不同的权重。

1.2 随机森林模型

随机森林模型[17]作为一种集成学习模型，其基础学习机为决策树，采用Bagging策略。为了增加每个决策树的随机性，以增加不同树之间的差异性，在每个决策树的生成过程中，采用随机子空间策略。随机森林模型的算法示意图如图3所示。

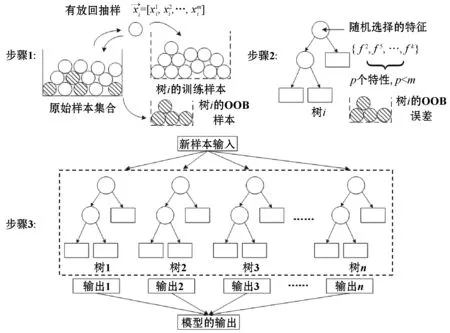
图3 随机森林模型算法示意图

如图3所示，随机森林模型的算法分为3步，其基础学习机为决策树，本文约定树的数目为N，样本数目为T，输入特征数目为P，算法具体如下。

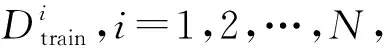
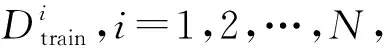
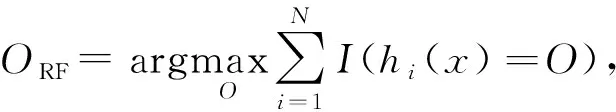
随机森林模型的一个优点是其可以在训练的同时进行泛化误差的估计，即OOB估计。如图1所示，每个决策树有各自的OOB样本，这些样本在该决策树的训练过程中未被使用，因此可利用这些样本来估计模型的泛化能力，而不像其他模型一样，需要借助交叉验证的方法单独估计泛化误差。根据理论推导，随机森林模型的泛化误差上界可表示如下:

(1)

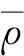
一般的，模型的泛化误差可以解释为由偏差和方差引起。对于随机森林模型，其偏差的期望与各个基础学习机偏差的期望相等，即随机森林模型一般不会显著降低模型的偏差，但其可以显著减小模型的方差。假设各个决策树的方差均为σ2，则随机森林模型的方差可大致表示为：

(2)

由式(2)可知，当各个决策树的相关性较小时，随机森林模型的方差会显著下降。因此，Bagging策略一般需要准确性较高的基础学习机，其基础学习机决策树模型不进行剪枝，整个模型通过降低方差的方式提高泛化性能。

1.3 梯度提升算法

集成学习的主要策略有Bagging与Boosting，且各有优势与不足。随机森林模型采用Bagging策略，可以减小模型的方差，但难以显著降低偏差，因此要求基础学习机具有相对较高的准确性。Boosting策略则可以降低模型偏差。原理上讲，即使采用了准确度相对较低的基础学习机，也可以通过逐步提升的方式，提高整个模型的准确性。在Boosting策略中，使用较多的有AdaBoost模型和GBDT模型，其训练过程本质上采用的是前向分步(forward stage-wise)算法，整个模型是一种加法模型，采用Boosting集成学习策略的模型可表示如下：

(3)

式中：集成学习模型FM(x)由M个基础学习机模型线性组合而成，fm(x)为第m个基础学习机，αm为第m个基础学习机的权重。下一步便是如何训练各个基础学习机，AdaBoost和GBDT分别采用不同的方法进行训练，其中AdaBoost通过对训练样本分配权重，然后根据分类正确与否更新权重的方式训练不同的基础学习机，GBDT则采用梯度提升方法进行训练。一般AdaBoost适用于分类问题，如果要应用于回归问题，需要做一定的改进，如AdaBoost.RT方法[18]；GBDT方法可直接用于分类和回归问题。本文中的出清电价预测属于回归问题，因此使用梯度提升方法进行模型的训练。

梯度提升算法的原理是基于泛函的梯度下降法，首先定义目标函数如下:

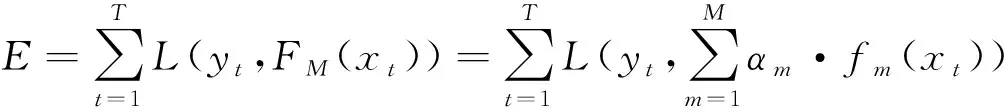
(4)

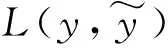
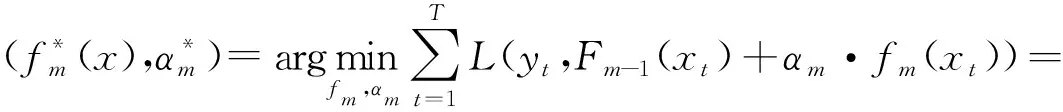
(5)

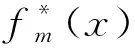
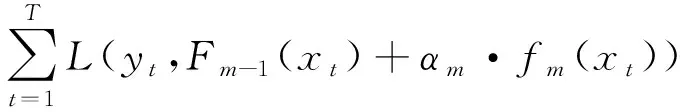
(6)

根据梯度下降法的原理，最佳模型应为目标函数的负梯度方向，即：

(7)

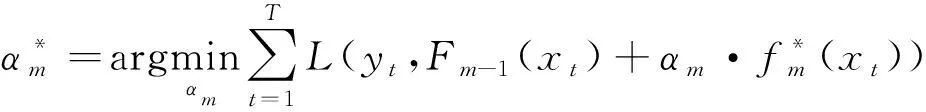
(8)

重复以上过程，直到训练完成所有的M个基础学习机及其系数，最终按照式(3)得到集成学习模型。应用梯度提升算法的集成学习模型，采用了加法模型，后续的基础学习机模型能够在前面各个基础学习机模型的基础上，进一步提高精度，因此可以降低模型的偏差，这是其与Bagging策略的不同之处。其基础学习机可以是准确性不高的模型，通过提升方法，逐步提高整个模型的准确性，但同时，也存在一定的过拟合风险[19]，而不容易过拟合正是随机森林模型的优势之一[16]。

1.4 梯度提升随机森林模型算法

以上两小节分别介绍了采用Bagging和Boosting集成策略的模型及其优点与不足，随机森林模型不容易过拟合，但其要求基础学习机具有相对较高的准确性，不会显著降低偏差；梯度提升算法可以逐渐地降低模型偏差，但仍存在过拟合的风险。因此，为了提高出清电价预测的准确性，本文提出将两种集成策略结合，以发挥各自的优势，同时避免其不足。思路是，在梯度提升模型中，基础学习机不再采用简单的基础学习机，如决策树等，而是采用随机森林模型。即首先使用随机森林模型将众多决策树并行训练，得到一个方差较小的基础学习机模型，然后再利用梯度提升算法可以降低偏差的特点，在随机森林模型的基础上，进一步降低模型的偏差。通过较少次数的梯度提升训练，便可在随机森林模型的基础上，进一步降低模型的偏差，从而降低整个模型的偏差和方差，提高模型预测的准确性与稳定性。

首先定义模型训练的目标函数，实际中一般采用平方误差函数：

(9)

式中：fm(x),m=1,2,…,M为随机森林模型。然后，根据梯度提升方法，对第m个随机森林模型，计算目标函数关于Fm-1(x),m=2,3,…,M的负梯度，作为第m个随机森林模型的目标值。

(10)

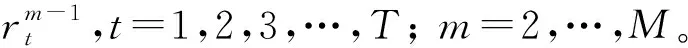
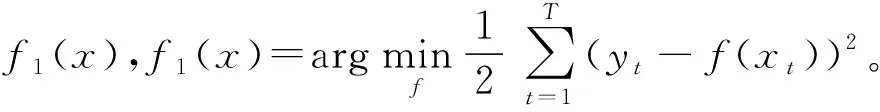
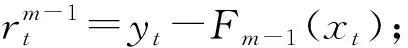
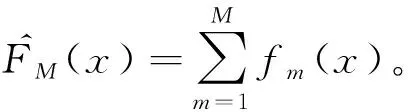
通过以上算法，结合随机森林模型不容易过拟合的优点和梯度提升方法可降低模型偏差的优点，进一步提高模型预测的准确性与稳定性。本文提出使用梯度提升随机森林模型进行电价的预测，其预测流程如图4所示。

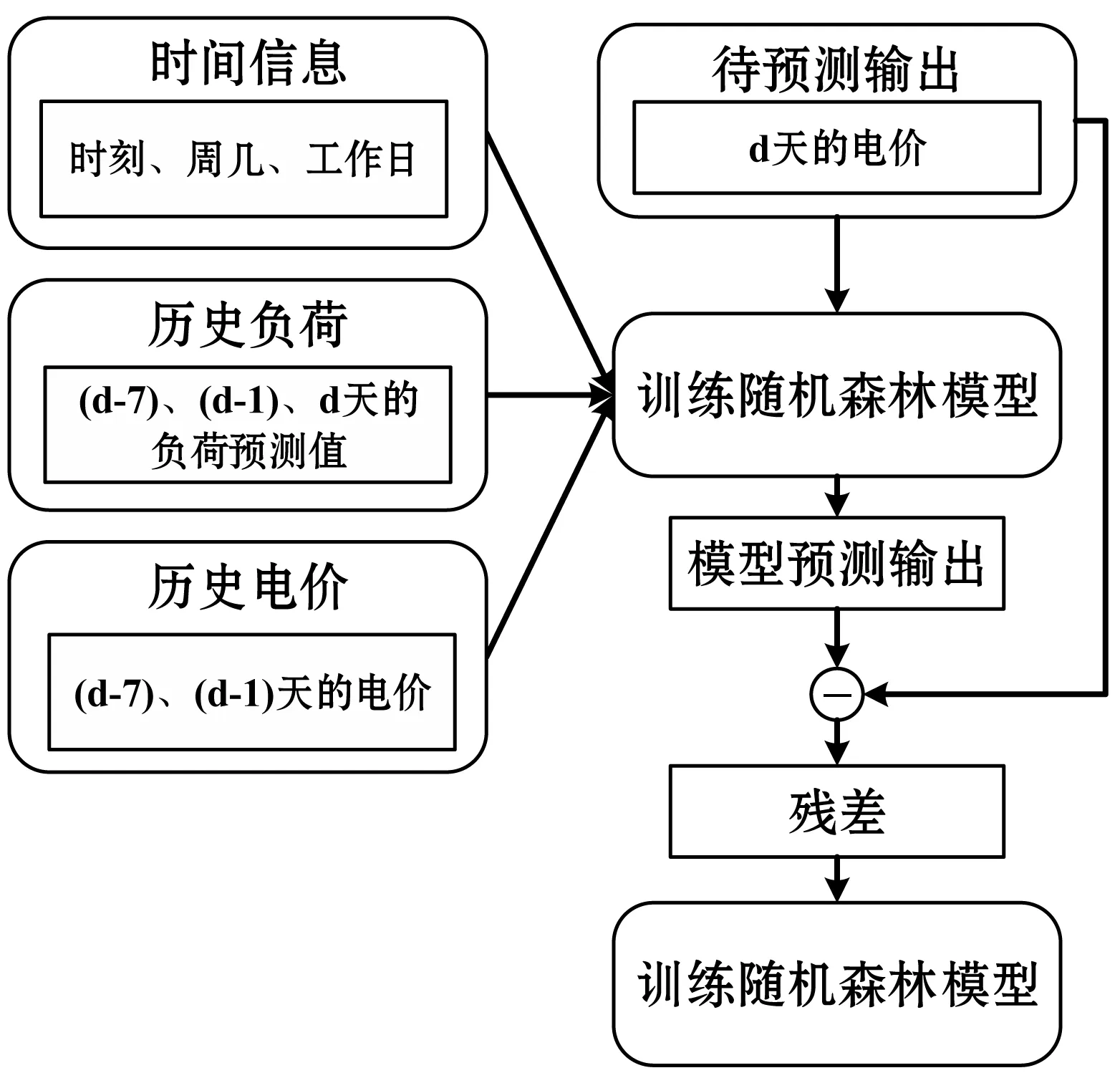
图4 基于随机森林模型的电价预测流程

首先确定电价预测模型的输入特征。影响电价的因素很多，但对其影响程度较大的主要是时间因素、电网负荷和历史电价等。其中，时间信息包括当前时刻、交易日为周几等，因为电价序列中有一定的周期性。负荷信息中包括一周前对应时刻的负荷值、一天前对应时刻的负荷值，以及待预测时刻的负荷预测值等。历史电价信息中包括一周前和一天前对应时刻的电价值。以上为模型的输入信息，模型的输出则为待预测时刻的电价Y。将这些信息输入第1个随机森林模型，训练得到f1(x)，便得到该模型对训练样本的估计O1。根据梯度提升算法，计算二者的残差r1=Y-O1。下一步，基于原始输入信息和残差r1训练第2个随机森林模型f2(x)，类似的，计算其对训练样本的估计O2，然后继续计算残差r2=Y-O1-O2=r1-O2。按照以上过程不断重复，直到训练完成M个随机森林模型。当有新的样本输入时，可同时输入到M个随机森林模型中，最后将各个模型的输出求和后，得到梯度提升随机森林模型的预测值。

2 实验结果与分析

2.1 样本选择

本小节使用美国PJM日前电力市场的数据对本文提出的预测算法进行验证，收集PJM电力市场2014年9月至2017年2月的数据进行验证。使用2016年9月之前的数据作为训练样本，剩余的作为测试样本。训练样本包括2年的数据，测试样本包括半年的数据。每一个交易日包含24个负荷值与24个电价值。使用图4所示的方式训练模型并对交易日某时刻的电价进行预测。

2.2 实验设计与结果分析

为了验证本文提出预测模型的效果，设计实验进行验证。梯度提升随机森林模型中，需要设置某些对模型结果有较大影响的超参数(hyper-parameter)，包括随机森林模型中决策树的数目N、决策树算法中每个节点处随机选择的特征数目p、梯度提升框架中随机森林模型的数目M。对于超参数p，本组实验中设置p=5。对于其他的超参数，则通过设置不同值进行对比。

随机森林模型的超参数N对模型预测精度一般有较大的影响，因此在实验设计中，对比不同N值，分别设置N值为10、20、50、80、100、200、500、800、1 000。梯度提升模型中随机森林的数目M依次设置为2、3、4、5。为了验证本文提出模型的有效性，分别使用随机森林(RF)模型和提升树(GBDT)模型进行对比实验，两个模型分别采用了Bagging策略和Boosting策略，通过将其与本文模型对比，可验证本文提出的算法能否将两种集成策略的优势结合，进一步提高模型的预测准确性，在对比模型中采用同样的超参数设置。

在GBRF模型中，随机森林模型的个M可取不同值，根据实验结果发现当M=2时模型的预测准确性已经较高，再增加模型的个数，会增大计算量，但并不会显著提高模型的准确性，因此在实验中，GBRF模型的M设置为2。

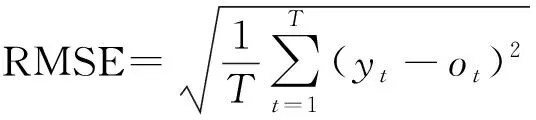
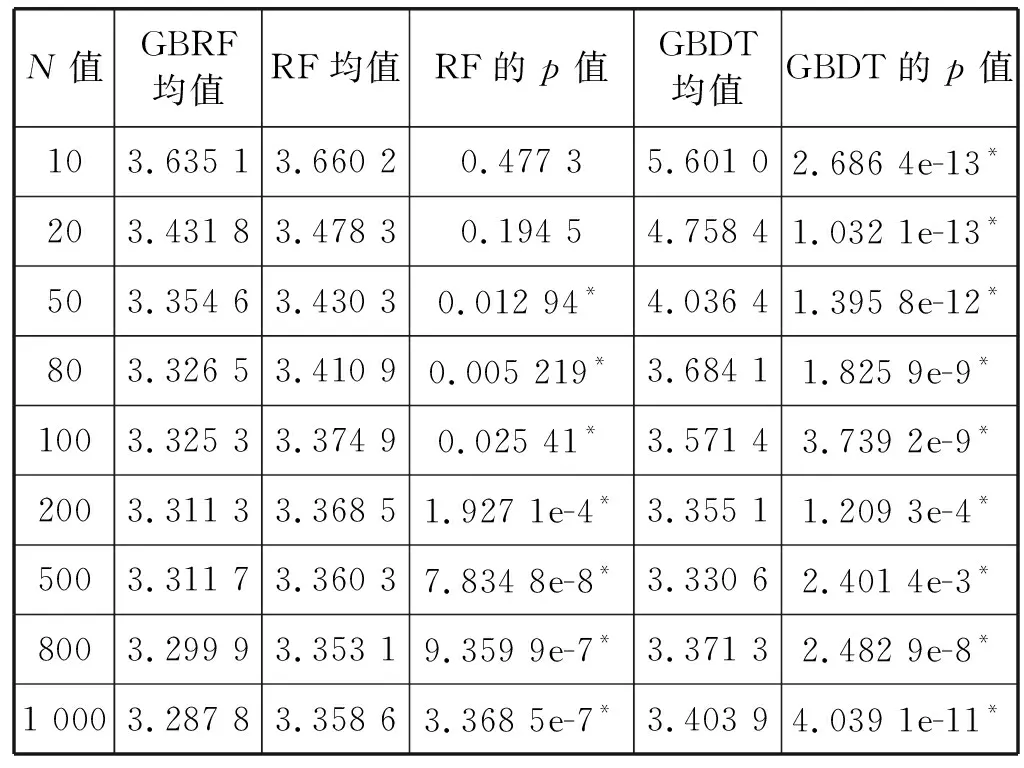
表1 不同N值下各个模型RMSE的对比结果

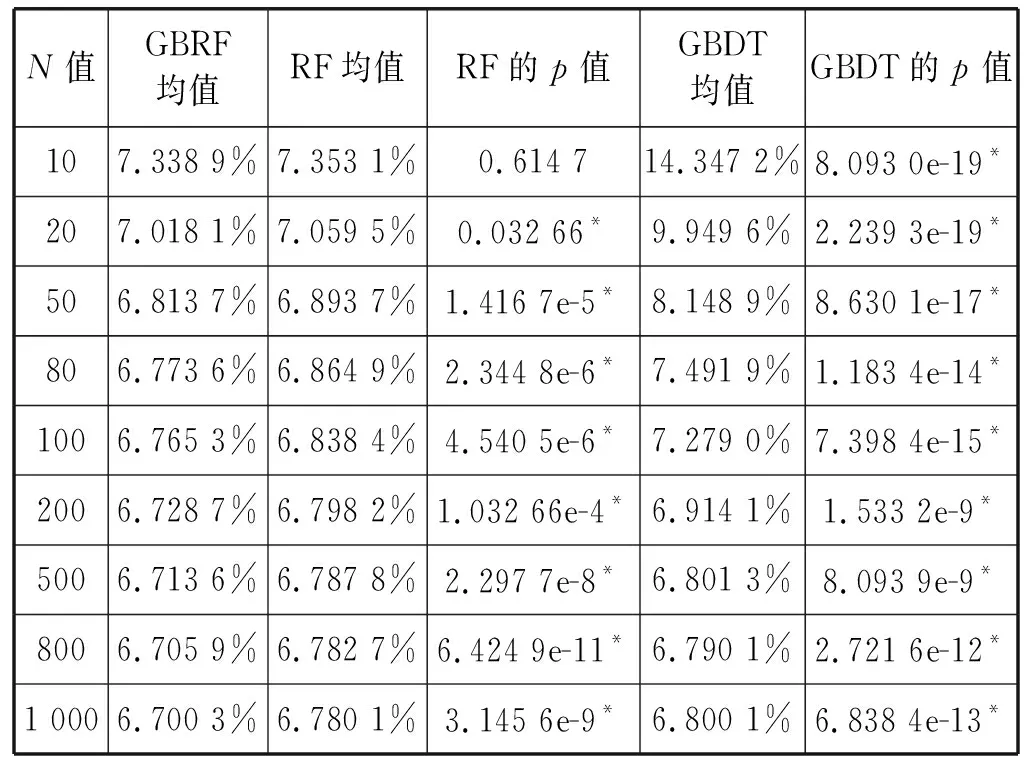
表2 不同N值下各个模型MAPE的对比结果

表1、表2中，GBRF为本文提出的模型，RF为随机森林模型，GBDT为梯度提升树模型，每个模型运行10次，分别统计10次的RMSE和MAPE的均值，并将两个模型的10次误差分别与GBRF模型的结果进行t检验，以确定两个模型的平均预测准确性是否有显著差异。表格中显示t检验的结果p值，当p值小于0.05时，可认为该模型与本文提出的GBRF模型有显著的差异，表格中具有显著差异的p值均以下划线方式标出。

可以看出，本文提出的GBRF模型的预测精度在统计意义上优于对应的RF模型和GBDT模型。对比GBRF模型与RF模型，可看出，当N大于等于50时，GBRF模型的准确性优于RF模型，这说明在第1个RF模型的基础上采用梯度提升算法，确实可以进一步降低模型的偏差，提高模型预测的准确性。对比GBRF模型与GBDT模型，可看出GBRF优于GBDT模型。二者均采用梯度提升算法，不同的是基础学习机，GBRF采用RF作为基础学习机，可以仅使用2次迭代，便达到较高的准确性，而GBDT采用决策树作为基础学习机，需要多次迭代才可完成模型训练，说明采用方差相对更小的模型作为基础学习机，可以使用更少次数的梯度提升，达到相对较高的准确性。因此，GBRF模型通过使用RF模型作为基础学习机，降低模型的方差，通过使用梯度提升算法，在RF模型的基础上，进一步降低模型的偏差。结果表明，本文提出的GBRF模型可以有效结合两种集成学习策略的优势，进一步提高模型的准确性。

为了直观对比不同模型预测准确性的差异，将以上3个对比模型的RMSE和MAPE绘制如图5与图6所示。由表1和表2的结果可看出，当N小于80时，GBDT模型的预测误差相对较大，为了更准确的观察不同模型的差异，图中只绘制N大于等于80时各个模型的结果。

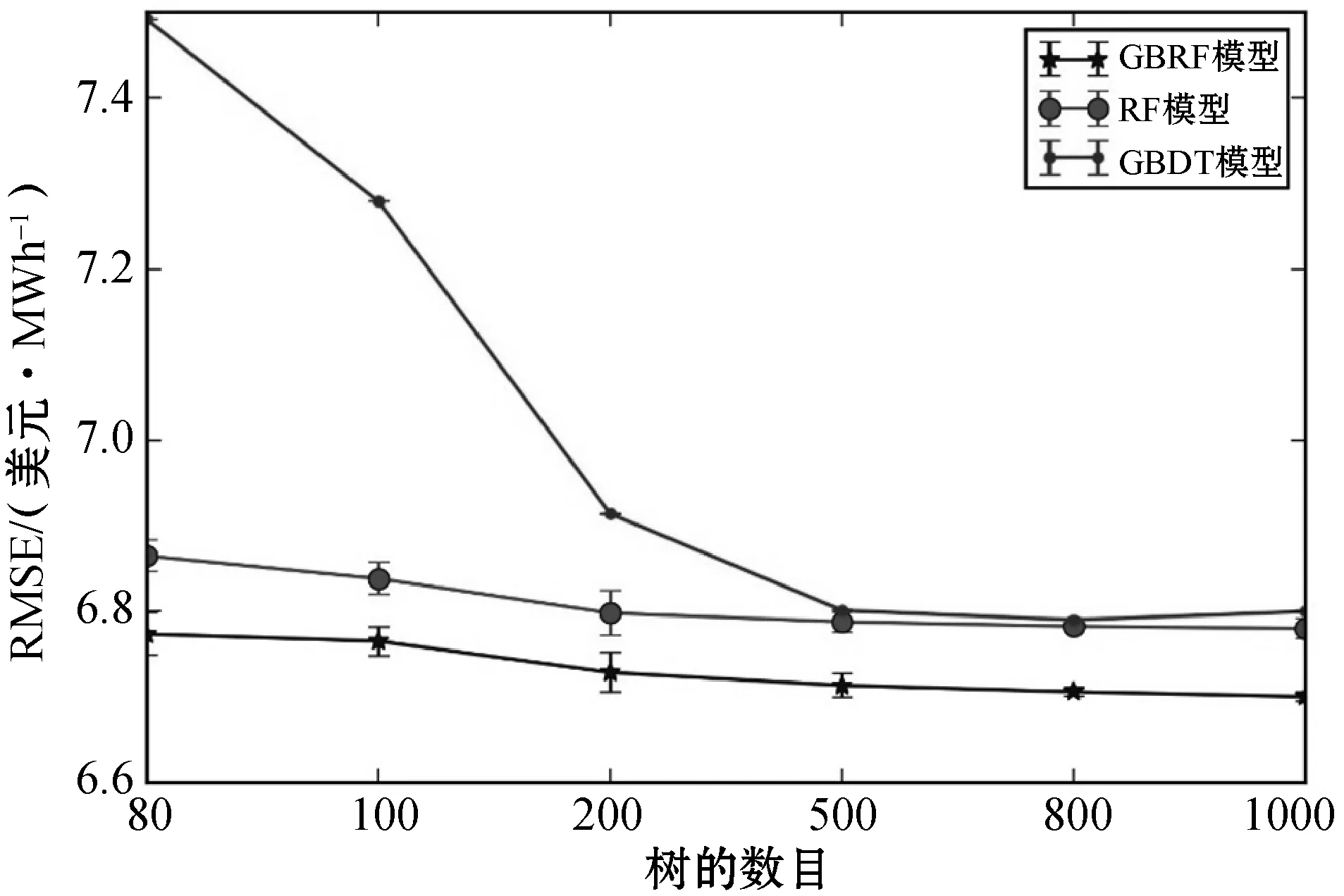
图5 不同模型RMSE对比

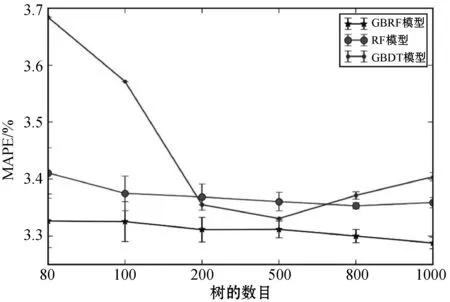
图6 不同模型MAPE对比

图中分别展示了3个模型在不同N值时RMSE和MAPE的均值与标准差，分别代表模型的准确性和稳定性。可以看出，GBRF模型的准确性优于RF模型和GBDT模型。GBRF模型与RF模型的变化趋势几乎相同，但二者之间一直存在一定的差距，说明在RF基础上，本文提出的GBRF模型确实可以进一步提高准确性。观察RF模型，随着N值的增大，模型只能逐渐减小方差，而无法显著提升模型的准确性，而采用梯度提升方法改进之后，GBRF模型的方差仍与RF相仿，但准确性却显著提升，这说明，采用梯度提升算法，在保持方差较小的前提下，确实可以降低模型的偏差，验证了本文提出算法确实可以将二者的优势结合。

总结而言，本文提出的梯度提升随机森林方法，有效结合了Bagging和Boosting两种集成学习策略的优点，可以在随机森林模型的基础上，进一步提高模型的预测准确性。

3 结 语

为了提高出清电价预测的准确性，本文提出梯度提升随机森林模型，可有效结合Bagging和Boosting两种集成学习模型的优点，进一步降低模型的偏差。GBRF模型使用随机森林模型作为基础学习机，借助随机森林模型方差较小的优点，在其基础上采用梯度提升学习算法，借助提升算法可有效减小偏差的优点，在保持方差较小的前提下，进一步降低偏差，最终得到的模型具有较小的偏差与方差。将模型应用于PJM日前市场的电价预测，经过实验验证，该模型优于随机森林模型和提升树模型，能够在随机森林模型的基础上，进一步提高模型预测的准确性。