基于决策树的钢铁企业蒸汽管网调度规则系统

马 湧 孙彦广

(冶金自动化研究设计院混合流程工业自动化系统及装备技术国家重点实验室 北京 100071)

0 引 言

蒸汽是钢铁企业生产和生活所必需的能源，蒸汽能耗占企业能耗总量的10%左右。在大型联合钢铁企业里，蒸汽系统具有大时滞、大惯性、非线性等特点的复杂对象。面对这样的复杂运行状况，管理人员基本还是依靠多年来的生产所运行积累下的经验指挥系统运行[1]，难以避免发生放空、降质使用等情况，造成极大的浪费。国内外学者对此展开了研究，文献[2-4]的研究对方程求解易于陷入局部最优解，造成得到解是非最优解。文献[5]根据特定企业生产实际，从供应和生产两端分别入手进行求解，该方法通用性有待改进。

本文基于钢铁企业蒸汽调度历史记录，建立决策树模型，并进行调度规则求解，得到优化的企业调度规则系统，从而有效提高管网操作水平和效率，保证管网高效安全运行。

1 某钢铁企业蒸汽管网概况

某钢铁企业蒸汽管网由S1、S2、S3三个压力等级管网构成。S1管网压力相对较高，其汽源和用户数量较少，结构简单。S2管网有8个供汽源和20个主要用户。S3蒸汽管网又称作低压蒸汽管网。该钢铁企业蒸汽管网系统整体结构图如图1所示。

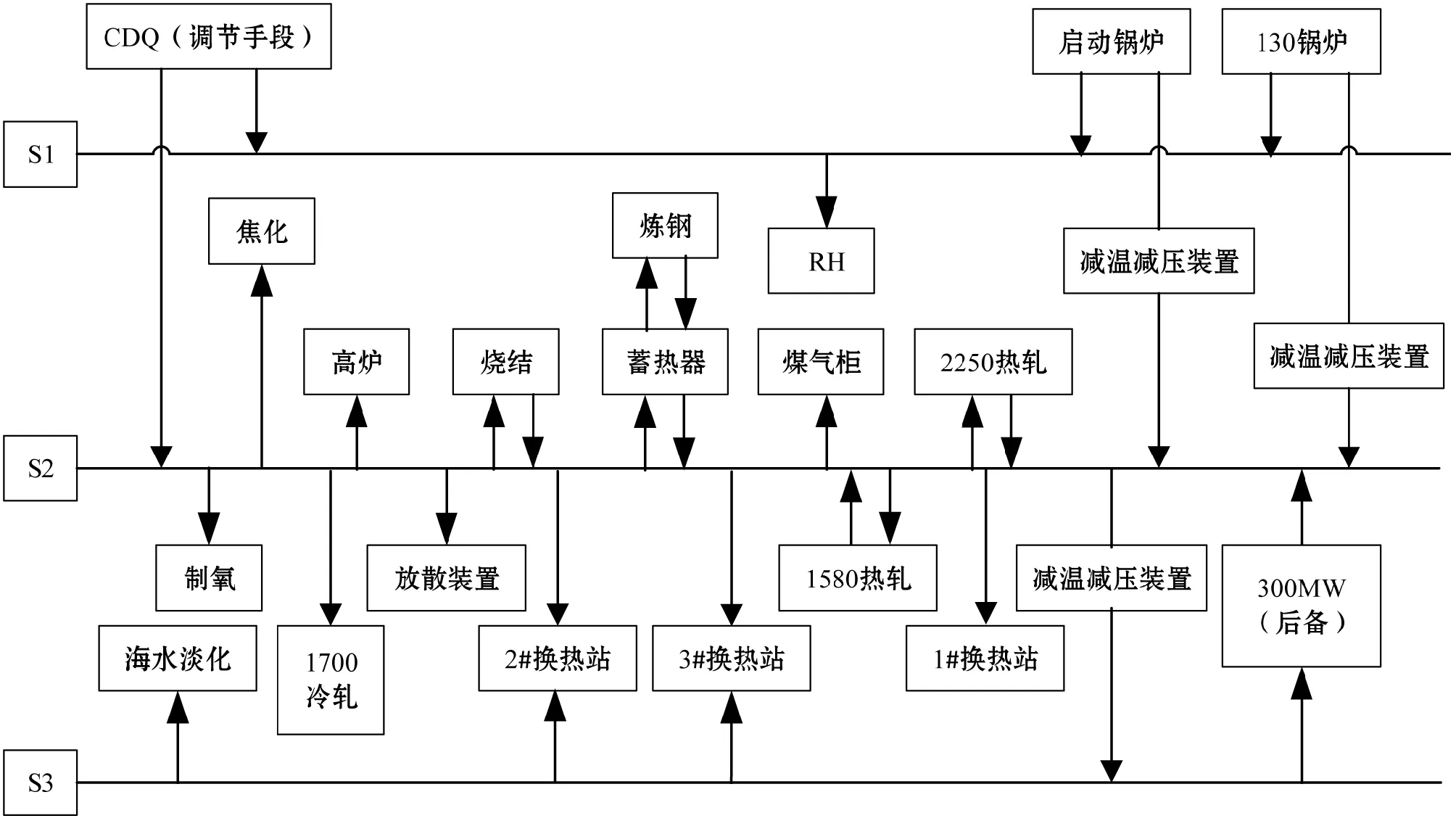
图1 某钢铁企业蒸汽管网结构图

该钢铁企业蒸汽系统是多汽源、多用户系统，其日常调度严格按照事先制定规则执行。例如，以一个管网的波动周期为例，根据企业的调度规则，当管网压力处于上升区间时，首先判断汽源锅炉是否还有可调节余量，若有则调控汽源锅炉，减少供汽量最大调节幅度每次10 t/h；若压力继续上升并超过A2则调节CDQ汽轮机，减少抽汽量，增大发电功率；若压力超过A3，则增大海淡产量，以及提高换热站使用S2的蒸汽量；若压力继续升高，则要开启放散阀以保证管网的运行安全。

反之，当压力低于正常运行值时，首先增加汽源锅炉供汽量，若达不到目标要求，则增加CDQ抽汽量，压力持续降至A6则需海淡减产，换热站增用S3，减少S2用量，直至调整300 MW发电机组增加供汽量。调控过程如图2所示。

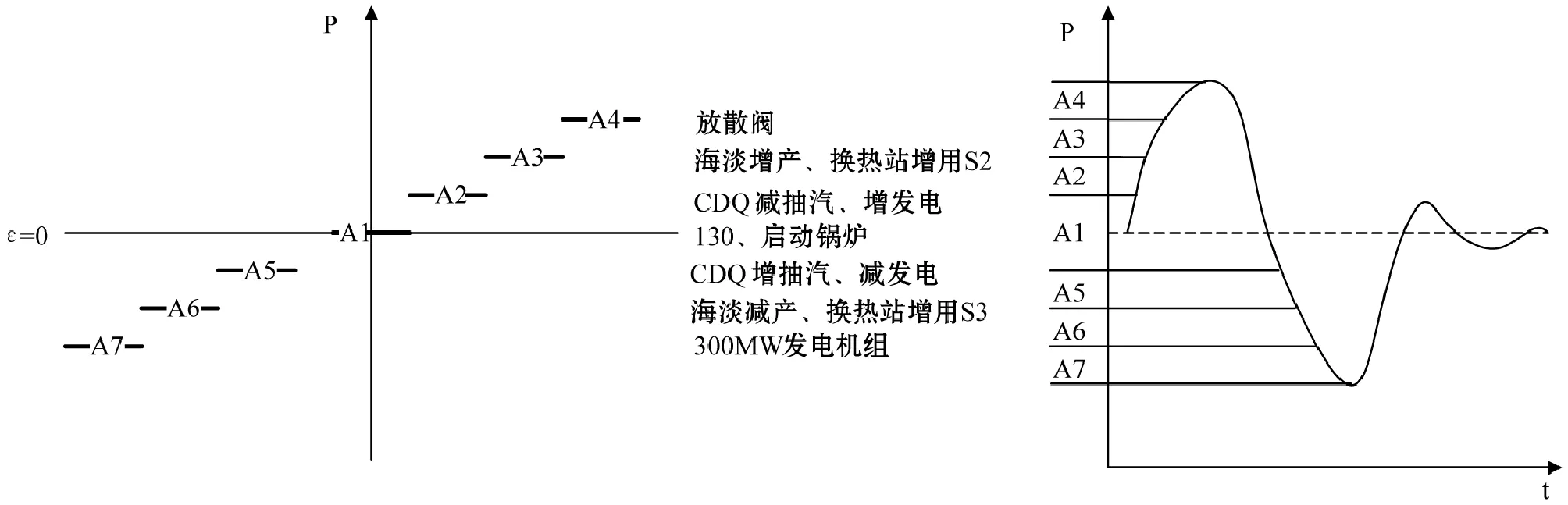
图2 一个管网波动周期内调控示意图

在该大型钢铁企业蒸汽管网系统中，S1管网用户单一，且规模较小，其控制和调度较为简易。S3管网为低压管网，用户均为稳定长期低压用户，管网波动较小，对管网冲击有限。S2管网连接几乎全部的生产用户和所有供汽源，波动频繁，对管网的冲击较大，因而S2管网调度难度最大。

蒸汽系统运行的调度控制指标分为三个区间，分别是：绿区，0.7～0.85 MPa，正常工作区间；黄区，0.6～0.7 MPa，0.85～0.95 MPa，偏离正常状态、需调整区间；红区，小于0.6 MPa，大于0.95 MPa，不能满足生产或极有可能引起生产故障的非法区间。

总的调度原则是保证管网大部分时间在绿区运行，减少黄区运行时段，消除红区运行工况。

2 决策树方法及理论

决策树是一种算法结构，其结构即为决策型树状结构，与流程图的树形结构类似[6]，树的根节点是顶层节点。决策树的选择分裂规则很多，属性选择度量方法是较为常见的一种[7-9]。其主要思想为一种启发式方法，即将给定类标号的训练样本集的数据S按照“最纯”的标准划分为单个类。在建立决策树算法的过程中，如何建立最佳分裂属性显得非常重要和关键，而属性选择度量的方法又多种多样，如信息增益、增益率、GINI(基尼)指标、距离度量以及相关度等方法[10]。本文所主要介绍的选择度量方法是信息增益属性度量方法。

1948 年，香农(C.E. Shannon)提出信息论后，把熵(Entropy) 定义为衡量一个系统混乱程度的统计量，其中熵值越大，则表明系统越混乱，反之则越小。信息论中对信息量(Information)和熵(Entropy)也分别作出明确的定义和解释：

Information=-log2(pi)

(1)

Entropy=-∑pilog2(pi)

(2)

式中：pi为该样本属于某类别的概率值。

• 划分前数据集的熵：

对于样本集合S，有s个数据；对于分类属性C划分了m个分别不同的离散值c1，c2，…，cm(即表明数据样本S最终要被分成m个类别)。样本数s1，s2，…，sm对应的分类属性值分别为c1，c2，…，cm。则划分之前，样本集S的总熵值：

(3)

式中：pi是S集中任意一个样本属于类别ci的概率，并用si/s估计。

• 划分后数据集的熵：

设{a1，a2，…，an}是属性A对应的n个不同的离散属性值，则可使用属性A将数据集S划分为n个子集{s1，s2，…，sn}，对应其中每个子集Sj中所有样本的属性A都是aj。

设子集Sj中的全部样本数为sj，其中分类属性值为c1，c2，…，cm的样本数为s1j，s2j，…，smj，则子集Sj的熵为：

(4)

式中：pij=sij/sj，是Sj中样本分别属于类别ci的概率。

使用属性A把数据集S划分成n个子集后，S的总熵为n个子集的熵的加权平均：

(5)

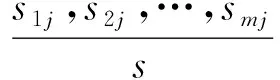
• 信息增益:

信息增益是用来表示系统中由于分类而获得的信息量，其量度是由系统熵的增减而定。把S划分前后的熵差定义为数据集S按属性A划分后的信息增益，公式如下：

Gain(A)=I(s1,s2,…,sm)-E(A)

(6)

3 实 例

钢铁企业蒸汽系统优化调控是一个极其复杂的问题，许多优秀的调度员在长期的工作中，通过对自己调度经验的总结与沉淀，形成了一些经验型的调度知识。这些调度知识不仅是钢铁企业的宝贵财富，同时也构成了钢铁企业能蒸汽态优化调控专家系统的知识库中的核心知识。专家知识主要包括主动调整和被动调整，其中主动调整包括主动计划调度和被动计划调度，被动调整是指事故状态下调度相关的调度原则。

以该大型钢铁企业蒸汽管网某时段内18条调度记录为例，调度记录中包括三个条件属性和一个决策属性。其中调度状态包括：主动计划调度、被动计划调度、事故状态调度；管网波动原因为导致管网管网不平衡的用户或者汽源；管网调节量是指需要达到管网平衡所需要调节的量；调度方案为决策属性变量，是最终调度人员采取的调度手段。调度人员值班记录如表1所示。

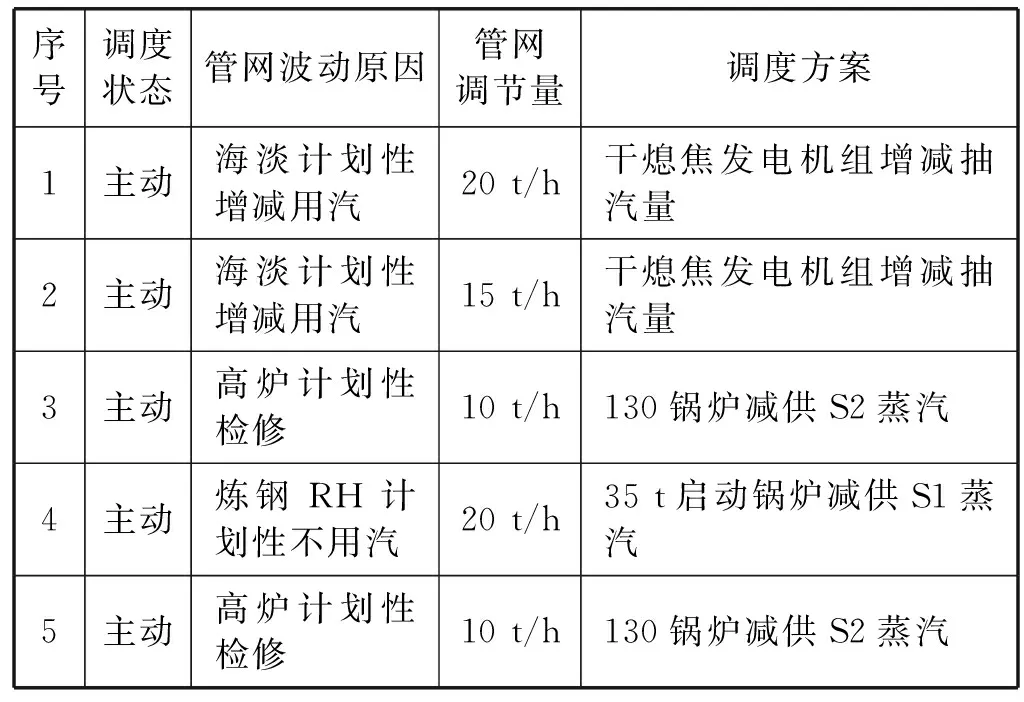
表1 调度人员值班记录表

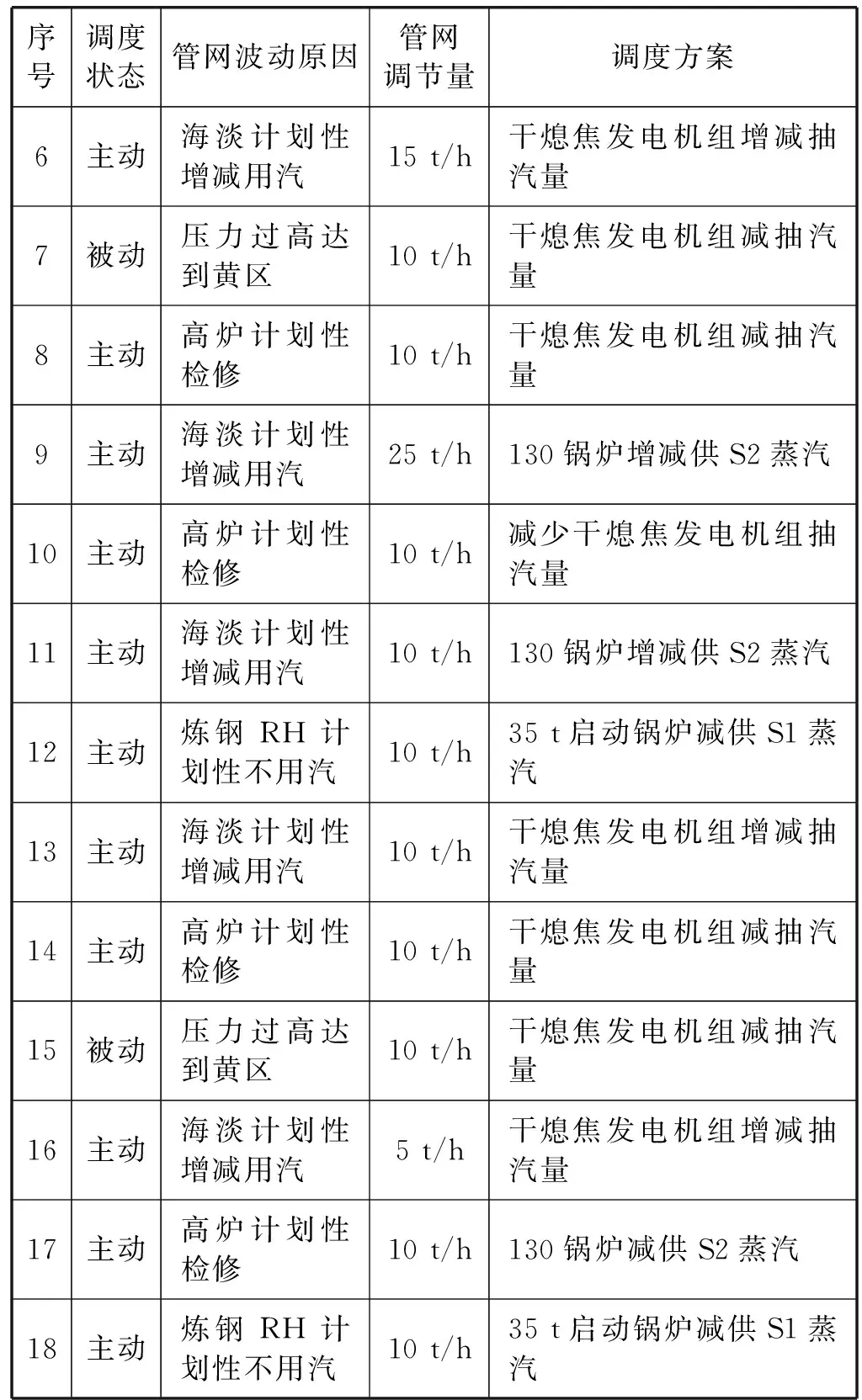
续表1

上述样本集S的总熵(期望信息)为：

0.471 1+0.513 3+0.430 8=

1.415 2

(7)

调度状态信息熵：

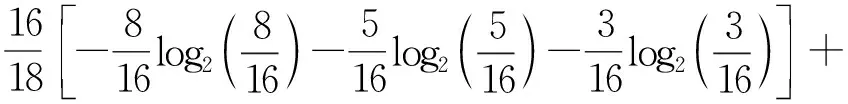
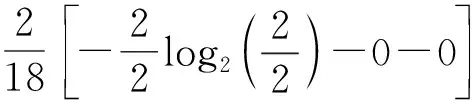
1.312 9

(8)

信息增益：

Gain(调度方式)=1.415 2-1.312 9=0.102 3

同理可得其他属性的信息增益：

Gain(管网波动原因)=0.015 5

Gain(管网调节量)=0.010 6

可以看出Gain(调度方式)最大，即有关调度方式的信息对分类帮助最大，提供最大的信息量。根据增益最大化原则，选择调度方式作为测试属性，将训练集分成两部分，即生成两个节点，然后再对这两个节点依次递归使用以上方法。生成决策树如图3所示。

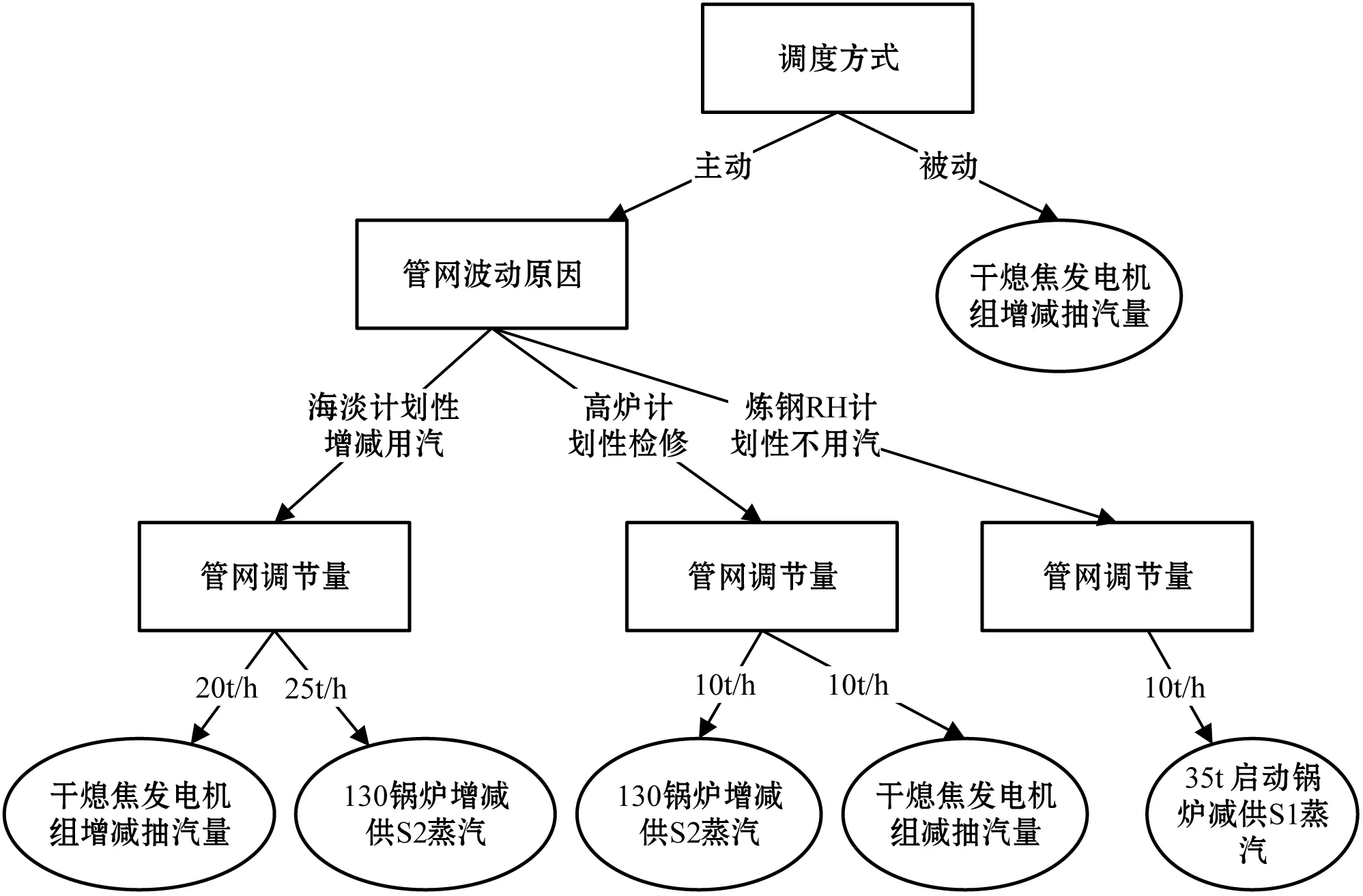
图3 蒸汽管网调度决策树

调度规则决策树的形成是基于现场的专家知识库系统以及事实库最终形成调度规则决策树，对于形成的决策树，按照“if-then”的形式从树根到树叶获取调度规则，更加适于计算机编程实现。例如数据集有属性X、Y、Z，可以得到的调度规则为ifX=“x1” andY=“y1” thenZ=“z1”。将上面树状的调度决策树表示成易于计算机语言来表示的“if-then”形式如下：

在主动调度方式下：

① IF (海淡计划性增减用汽&&调整量为20 t/h)

THEN {增减干熄焦抽汽量;}

② IF (海淡计划性增减用汽&&调整量为25 t/h)

THEN {130锅炉增减供汽量;}

③ IF (高炉计划性检修&&调整量为10 t/h)

THEN {130锅炉增减供汽量‖增减干熄焦抽汽量;}

④ IF (炼钢RH计划性不用汽&&调整量为10 t/h)

THEN {35 t启动锅炉减供S1蒸汽;}

在被动调度方式下：

IF (压力过高达到黄区)

THEN {干熄焦发电机组减抽汽量;}

在上述调度过程中，蒸汽调度的调整以保持管网平衡为基本原则，同时要符合产用汽设备的能力限制等条件。

选取该企业连续两个月正常生产情况下，前一个月采用原有调度方式，后一个月采用决策树系统进行调度。然后将两个月管网运行状况进行对比分析。在决策属系统应用前，管网运行的区间分布为：绿区占72.62%，黄区占27.05%，红区占0.33%。投入决策属系统后红区工况消除，黄区运行时间降至10.8%，绿区运行时间时间提高到89.2%。具体对比如图4所示。蒸汽决策树规则系统提高了管网运行效率和安全性能，对蒸汽系统的管理调度提供了有针对性的决策支持。

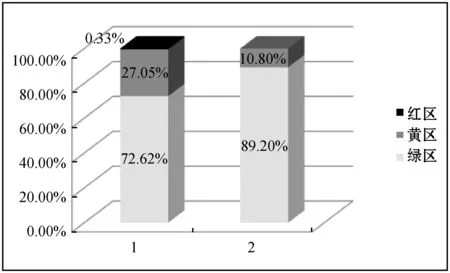
图4 决策树规则系统应用前后效果对比图

蒸汽系统是钢铁企业生产生活所必备能源之一，以上应用结果表明，建立一套有效的综合蒸汽管网调度控制系统可全面提升企业的蒸汽系统管理水平，保证蒸汽管网的安全高效运行。

4 结 语

本文以决策树方法理论为基础，研究了钢铁企业蒸汽管网调度规则系统。根据决策树原理的系统熵及决策属性等方法，结合现有企业调度规则库、专家知识库以及事实库，以典型的决策树算法建立某钢铁企业蒸汽管网调度规则决策树系统。验证表明，该决策树规则系统可大大提高管网绿区运行时间，减少黄区运行时段，消除红区工况，使得管网调度策略更加合理安全，有效提高蒸汽管网运行效率，保证管网更加安全运行。