基于综合改进随机森林算法的中国财政风险预警研究
2018-09-26刘新雯
刘 新 雯
(兰州交通大学数理学院 甘肃 兰州 730070)
0 引 言
风险是经济运行中的核心问题,财政生来就要承担公共风险。财政是所有经济活动的主要中心。一旦财政发生危机,它会对经济产生巨大冲击,甚至导致社会动荡[1]。所以应该精确地量化我国财政风险,并做出科学预警,使财政相关政策负责人有足够时间与依据来预防财政风险的发生,使财政危机的破坏度最大限度地降低甚至化解即将发生的危机,这具有非凡的意义。
随机森林(RF)算法是由Breiman提出的一种比较新的统计学习理论[2],其本质是一种组合分类器。该算法有高精度预测、强抗噪力、可调参数少、适应力强以及可避免“过拟合”等优点,在如生物信息学[3]、生态学[4-6]、医学[7-10]、网络安全[11-12]等领域都有广泛的应用。随着RF算法越来越受欢迎,其缺陷随之显现。近年来,一些学者在不同方面改进了RF算法。2010年,王爱平等[13]提出一种IERF算法,并将其应用于解决视频在线跟踪问题,经过反复实验验证其有效且稳定;2014年,曹正凤[14]为解决数据集不平衡问题提出C_SMOTE算法;2015年,陈斌等[15]提出了一种基于k-均值的基于KM-SMOTE算法,以解决由不均衡数据引起的分布式边缘化问题;2016年,Chaudhary等[16]针对多维分类问题提出一种改进的RF算法,有效提高了RF算法的精度;2017年,赵清华等[17]提出了基于SMOTE的改进算法TSMOTE(triangle SMOTE)和MDSMOTE(max distance SMOTE),达到降低算法复杂度的目的;2018年,贾文超等[12]提出一种基于特征选择的RF改进算法, 并将其应用于Webshell 检测研究中。
综上所述,本文提出了一种改进的RF算法,通过大量的实验验证了该算法,并与原始RF算法的性能进行了比较,结果显示,CIRF算法性能优良,同时也大大地降低了算法时间复杂度。
1 算法原理
1.1 Bagging算法
1996年,Breiman[18]根据Bootstrap思想提出Bagging算法。它是一种决策树的集成算法,其核心是应用Bootstrap重采样方法产生不同的训练样本集来训练各个决策树。其算法流程如下:定义示例样本集S={(Xi,Yi),i=1,2,…,n},其中每个样本的属性的数量为M,被划分为c个类别,测试样本x,决策树个数为N。则Bagging算法步骤如下:
1) 使用Bootstrap方法进行重采样,并随机生成k个训练集S1,S2,…,Sk。
2) 根据CART算法,每个训练集被用来生成相应的决策树C1,C2,…,Ck。
3) 将测试集X导入程序中测试每个决策树,产生相应的分类结果C1(X),C2(X),…,Ck(X)。
4) 根据k个决策树的分类结果,测试样本集X的分类是由决策树的多数投票方法决定的。
1.2 CART算法
1984年,Breiman等以信息熵为理论基础提出了CART算法。该算法以递归的思想构建决策树产生分类规则, 采用Gini指标最小原则进行节点分裂。
1) 样本的Gini系数:
(1)
式中:Pi代表类别i在样本集S中出现的概率。
2)每个划分的Gini系数:将S分隔成l个子集S1,S2,…,Sl,则此次划分的Gini系数为:
(2)
1.3 随机森林算法
原始随机森林RF是一种基于决策树的分类器集成算法。该算法将随机性引入训练集样本的提取与生成决策树节点分裂属性的选择中,并且最终采用简单投票法决定分类类别。它能够较好地解决单个决策树所存在的过拟合问题,有效提高了分类精度。RF算法步骤如下:
导入样本集S={(Xi,Yi),i=1,2,…,n},测试样本Xtest。
1) forj=1,2,…,N用bagging方法对对训练集进行抽样,以产生训练子集Sj(j=1,2,…,N);
2) 构造第j颗决策树的样本集为训练子集Sj;
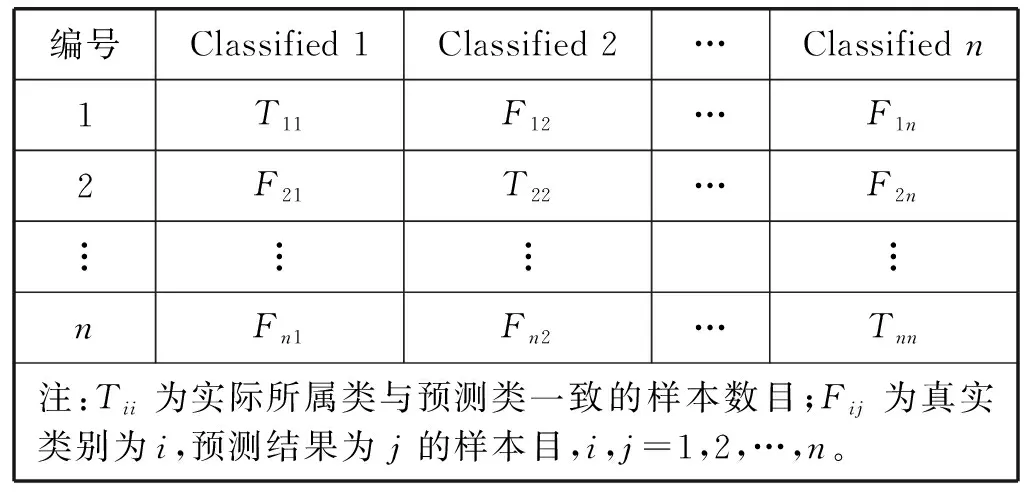
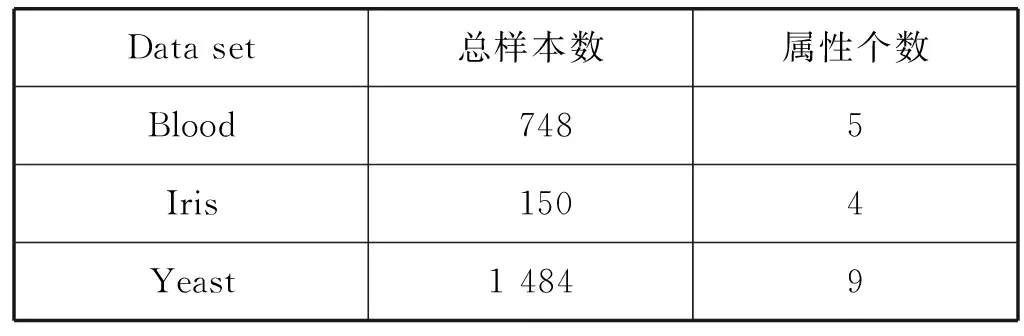
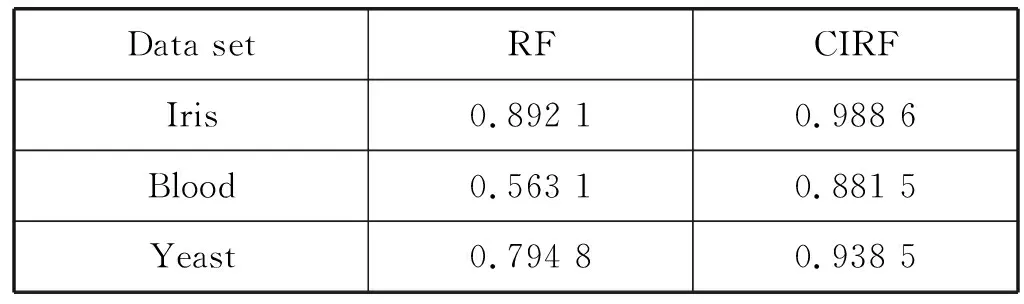
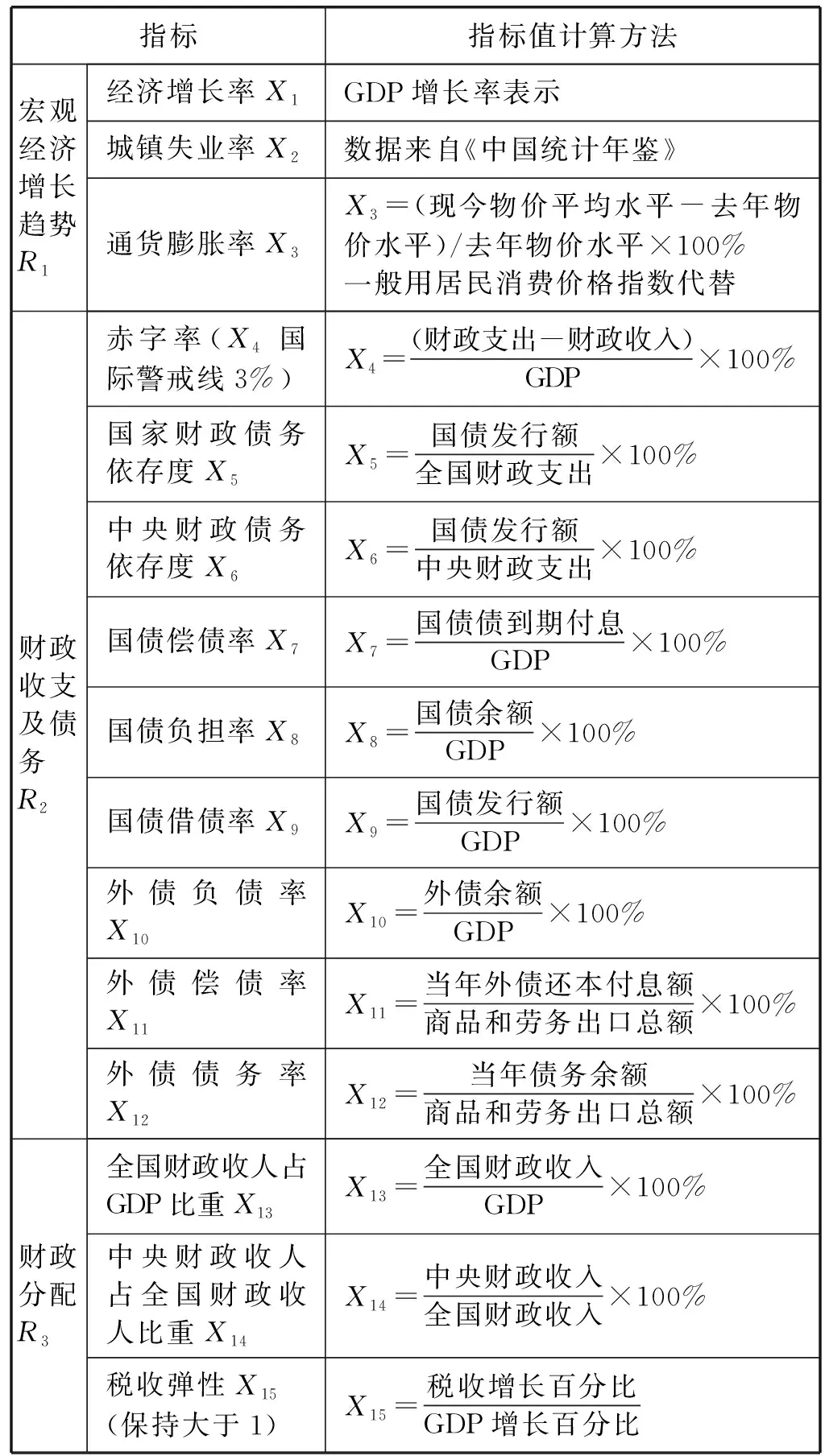
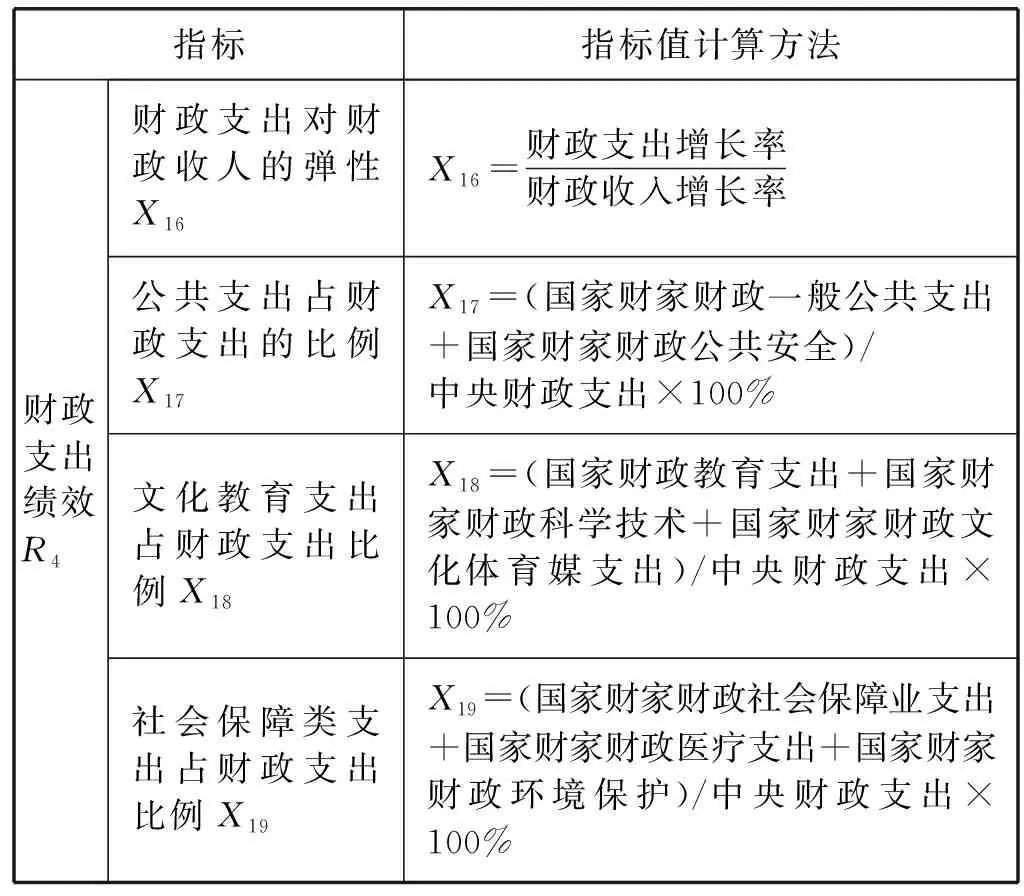
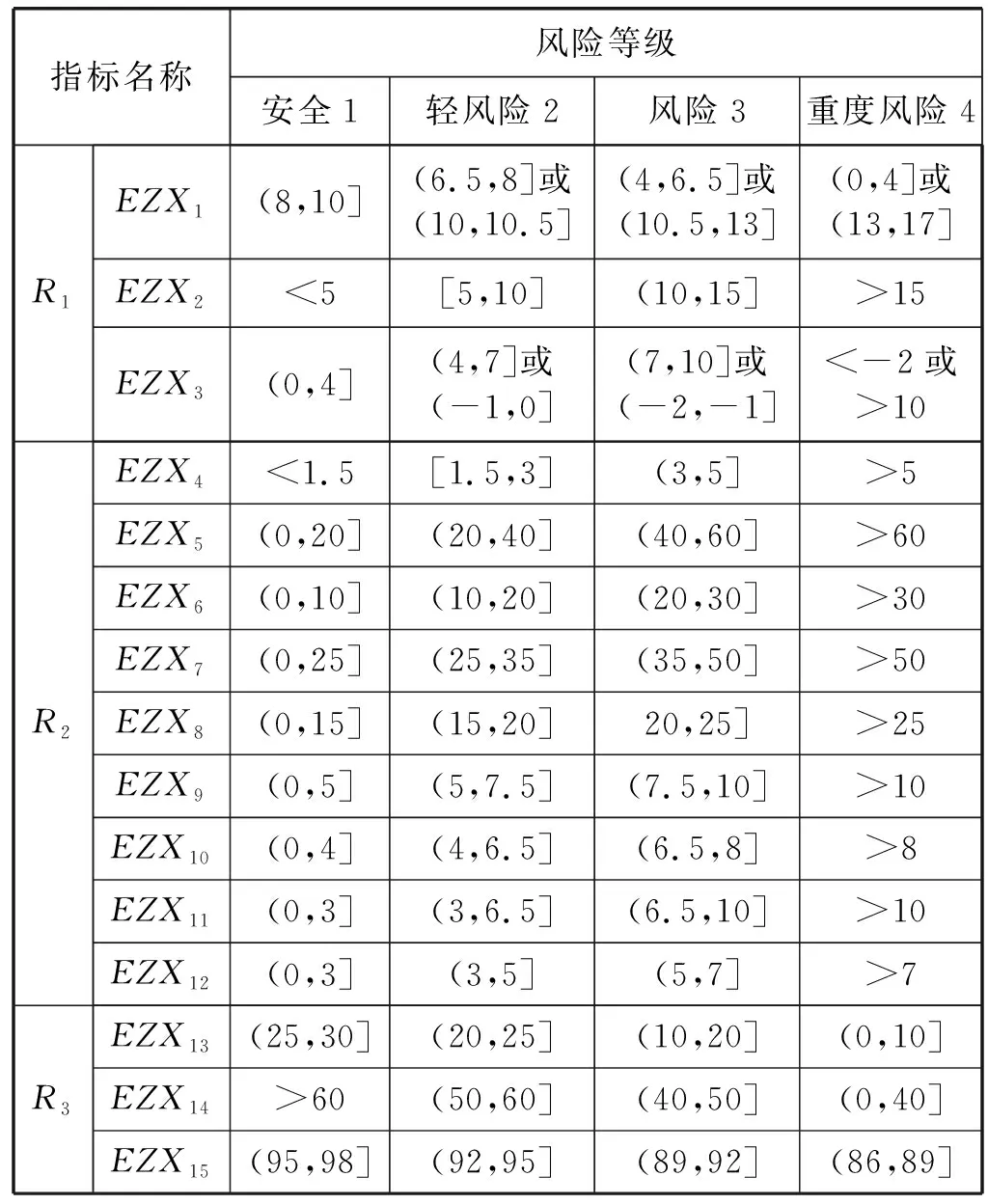
3) 随机选择样本属性中的m(m 4) 选择Gini指数最小的属性来分裂节点生成决策树,总共得到N个决策树; S_Bootstrap抽样算法是Bootstrap抽样算法的一种改进算法,根据已知的类别个数c将观测样本S分成c个子集S1,S2,…,Sc。对每个子集再进行Bootstrap抽样,进而产生小样本集s1,s2,…,sc,小样本集si的样本数由Si的样本数决定。然后将小样本集s1,s2,…,sc综合产生实验样本训练集SB={s1,s2,…,sj,…,sN}。 由于原始RF算法选择特征属性集合时采用完全随机选择方法导致决策树之间的相关性增强,从而降低了决策树的分类性能。故本文提出形似加权的一种特征选择方法。其核心过程为:首先根据已知类别将实验数据集SB划分为c个子集;然后对每个子集的特征进行因子分析,根据因子得分将特征M划分为公共特征Mshare,私有特征M1,M2,…,Mc和不重要特征Mleft;根据特征的重要程度构建特征子集,从而降低决策树间的相关性。 在改进的RF算法中,将分割节点的选定指标改为信息增益率,以最大信息增益率的节点作为分割节点。其相关计算如下: 1) 实验样本SB的信息熵为: (3) 式中:Pi代表类别i在样本集SB中出现的概率。 2) 在特征A的作用下,SB被划成l个子集SB1,SB2,…,SBl,则该划分的信息熵为: (4) 3) 信息增益(Gain): Gain(SB|A)=Entropy(SB)-Entropy(SB|A) (5) 4) 信息增益率: (6) 当原始的RF算法进行分类预测时,所涉及的每棵树的重要程度都相同,这可能忽略了决策树之间的差异性和对样本的判别出现不同的情况。故在该改进RF算法中引入一种加权集成的投票法则参与最终决策,并把基分类器的权重表示为如下的形式: (7) 式中:c为类别数,l为分裂子集数,Pil表示分类器Ti把样本X分成l类的概率。 再计算每个类别的置信度为: (8) 将2.1节-2.4节所提改进算法融合应用于RF算法中形成CIRF算法,其算法流程如下: 导入数据样本集S={(Xi,Yi),i=1,2,…,n},测试样本Xtest。 1) 使用S_Bootstrap方法从样本集S={(Xi,Yi),i=1,2,…,n}抽样,以产生训练子集sj(j=1,2,…,N); 2) 选训练子集sj为构造第j颗决策树的样本集; 3) 根据2.2节中的特征选择方法构建特征子集,并根据式(6)计算特征子集中各个属性的信息增益率; 4) 选择具有最大GainRatio值的属性作为分裂节点产生决策树,最后得到N颗决策树; 5) 将待测样本Xtest训练好的N颗决策树Tj(j=1,2,…,N)中,再根据式(8)计算各个决策树的置信度,并把置信度最大的类别作为算法的输出。 为不失一般性,该实验采用模型的精度作为随机森林分类性能优劣评价指标。该评价指标是在混淆矩阵(如表1)的基础上发展而来的。 表1 n维混淆矩阵 模型的精度表示所有正确分类在所有分类中所占比例: (9) 为验证改进算法的有效性,使用UCI数据库的3种不同的数据集作为实验数据集(见表2),对改进算法进行仿真实验。 表2 仿真数据集 仿真实验中,将实验数据的4/5当作训练集,1/5为测试集;每次实验重复1 000次。最终指标值是求解1 000次实验结果的均值得到。 实验结果分析: 在三种数据集上试验后,RF算法与CIRF算法的Accuracy值(决策树个数为10)如表3所示。 表3 RF算法与CIRF算法的精度值对比 由表3可知,在三种数据集中CIRF算法的Accuracy值在RF算法的基础上都有所提高。说明CIRF算法比原始RF算法有更好的分类性能。 衡量财政风险的指标有很多,本文所使用的指标大致可分为四组,分别用R1、R2、R3、R4表示,总计19个指标,具体指标与其计算公式见表4。 表4 财政风险衡量指标 续表4 根据各个指标的国际警戒线,本文将财政风险划分为四种状态,分别为“安全”(记为1)、“轻风险”(记为2)、“风险”(记为3)、“重度风险”(记为4),这里的得分是指数得分。具体的判定准则见表5。 表5 财政风险等级判断准则 再根据各个指标的指数得分,对财政风险等级进行划分。本文采用的财政风险等级划分准则[19]见表6。 表6 财政风险等级划分准则 续表6 1) 确定指标数据及其预处理 由于数据需求类别较多,大多数指标的月度数据与季度数据严重缺失,故本文选用1998年-2016年的年度数据作为实验样本数据。为了消减量纲不同对实验的影响以及方便后续财政风险程度衡量,将原始指标数据先进行标准化处理再进行指数化处理,处理后的指标用EZXi,i=1,2,…,19表示。处理后的部分数据见表7。 表7 衡量财政风险指标值 2) 确定指标权重 本文对各个指标采用因子分析的方法确定权重。首先分别对四组指标进行组内因子分析,结果见表8。然后再进行组间因子分析,结果见表9。 表8 指标组内因子得分 表9 指标组间因子得分 3) 实验数据整理 根据以上理论与计算,将原始数据进行整理,根据财政风险划分准则,可得出1998年-2016年的财政风险状况,部分数据见表10,数据详细信息见表11。 表10 1998年-2016年的财政风险状况 表11 财政风险实验数据信息 3.3.1 实验流程 将表10的完整数据作为实验数据集S={(EZXi,Ri),i=1,2,…,19},用1998年-2013年数据作为训练集,2014年-2016年数据作为测试集EZXtest,则基于CLRF算法的中国财政风险预警的具体实验流程如下: 导入数据样本集S={(EZXi,Ri),i=1,2,…,19},测试样本EZXtest。 1) 使用S_Bootstrap方法从样本集S={(EZXi,Ri),i=1,2,…,19}抽样,以产生训练子集sj(j=1,2,…,N); 2) 选训练子集sj为构造第j颗决策树的样本集; 3) 根据2.2节中的特征选择方法构建特征子集,并根据式(6)计算特征子集中各个属性的信息增益率(GainRatio); 4) 选择具有最大GainRatio值的属性作为分裂节点产生决策树,最后得到N颗决策树; 5) 将待测样本EZXtest训练好的N颗决策树Tj(j=1,2,…,N)中,再根据式(8)计算各个决策树的置信度,并把置信度最大的类别作为算法的输出。 3.3.2 参数设置 将决策树个数N分别设置为3、5、7、9、11、13、15、17、19、21、23、25、27、29、31,节点分裂属性个数设置为3,实验重复1 000次,结果均取其均值。 经过1 000次实验后,将其结果求均值得到不同决策树个数对应的模型精度值如表12所示。 表12 不同决策树个数对应的指标值 如图1所示,随着决策树个数的增加,评价指标的值也随之增加。当决策树个数达到19时,指标值达到最大值0.903 7,再增加决策树至23时一直不变,但当继续增加时,精度反而减小。故在随后财政风险预警试验中,决策树个数设置为19,节点分裂属性个数设置为3。表13是测试集数据EZXtest的实验结果数据。 图1 不同决策树个数对应的指标值对比 时间EZX1EZX2…EZX19R预测的R风险等级预测风险等级20140.371.53.5740.479 8 41.509 92220150.311.54.2432.112 2 33.270 52220160.281.174.6630.055 5 30.355 422 由表13可知,CIRF算法对2014年-2016年的财政风险预测分类完全正确,分类准确率达到100%,并且预测的综合得分与实际得分相比只差1个单位左右,预测的准确度相当高。所以,如果将该算法应用于财政风险预警工作中,可节省大量的人力和时间。 对2017年-2018年的财政风险进行预测,结果见表14(2017年的部分数据在公共数据平台上没有公布,故可将其作为预测的一部分)。 表14 财政风险的预测结果 由表14可知,2017年与2018年的财政都处于轻风险状态,不会对社会经济的正常运行和国家安全造成严重影响。 本文针对RF算法预测精度低的问题,提出一种CIRF算法。该算法对原始RF算法进行全方位的改进,采用UCI数据库中的三种数据集对该算进行仿真实验,并与原始RF算法作比较。结果显示,CIRF算法有更好的分类性能。因此CIRF算法可应用于各个领域。本文将其应用于中国财政风险预警中,预测结果显示,2017年与2018年的财政风险状态为轻风险,不会对社会经济的正常运行和国家安全造成严重影响。下一步,将针对随机森林本身在构建过程中存在的问题进行进一步的改进研究。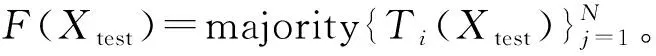
2 CIRF算法
2.1 S_Bootstrap算法
2.2 改进的RF特征选择方法
2.3 改进节点分裂算法
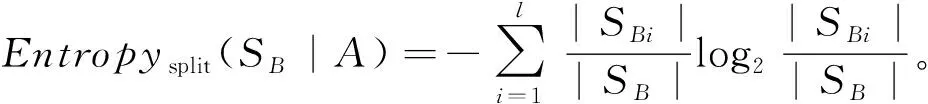
2.4 改进投票算法
2.5 CIRF算法流程
2.6 CIRF算法性能评价指标
2.7 CIRF算法性能验证
3 基于CIRF算法的中国财政风险预警
3.1 确定预警指标体系

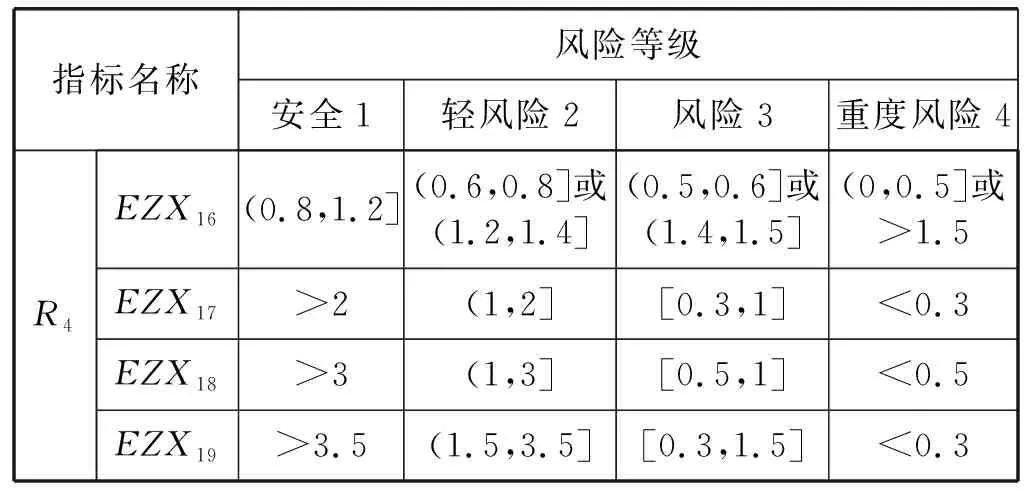
3.2 实验数据准备
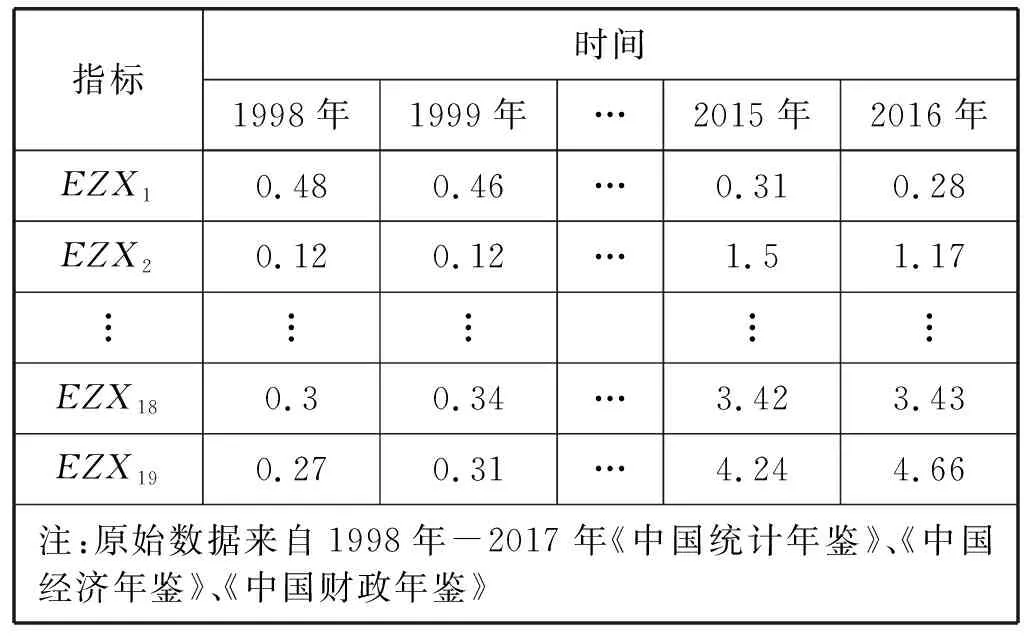
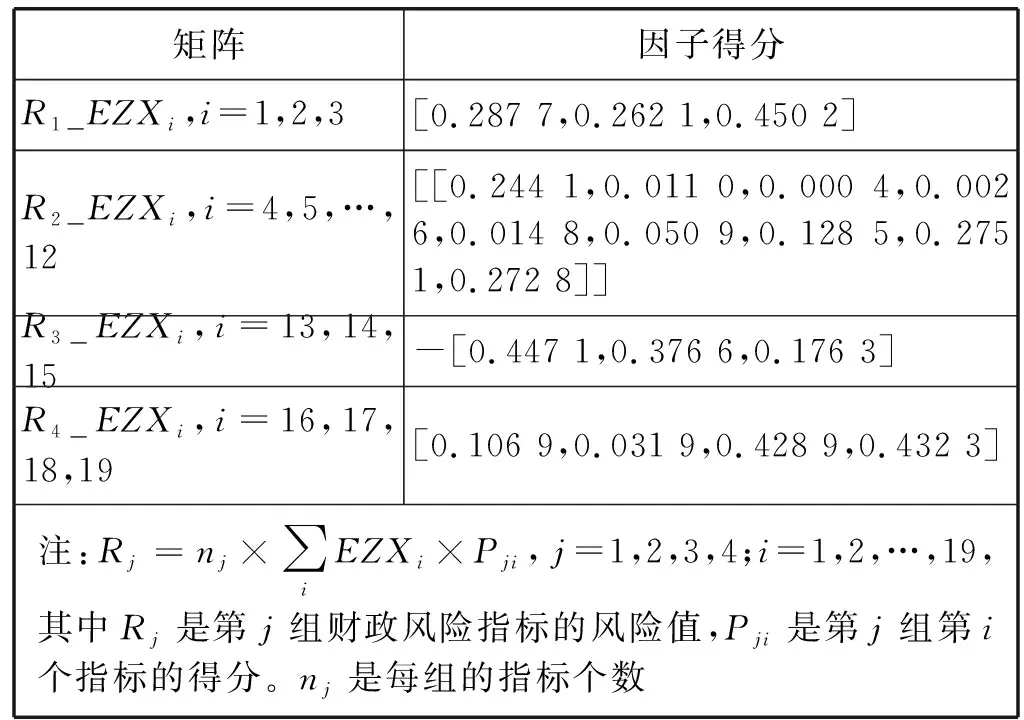

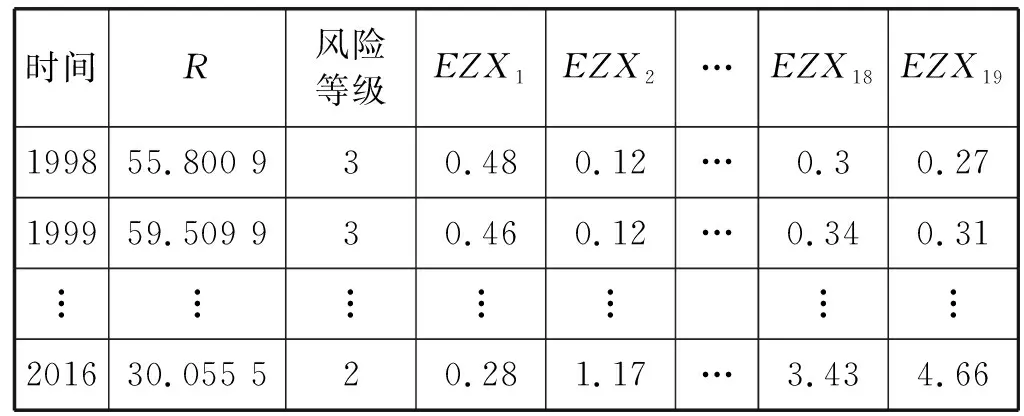

3.3 实验流程及参数设置
3.4 实验结果及分析
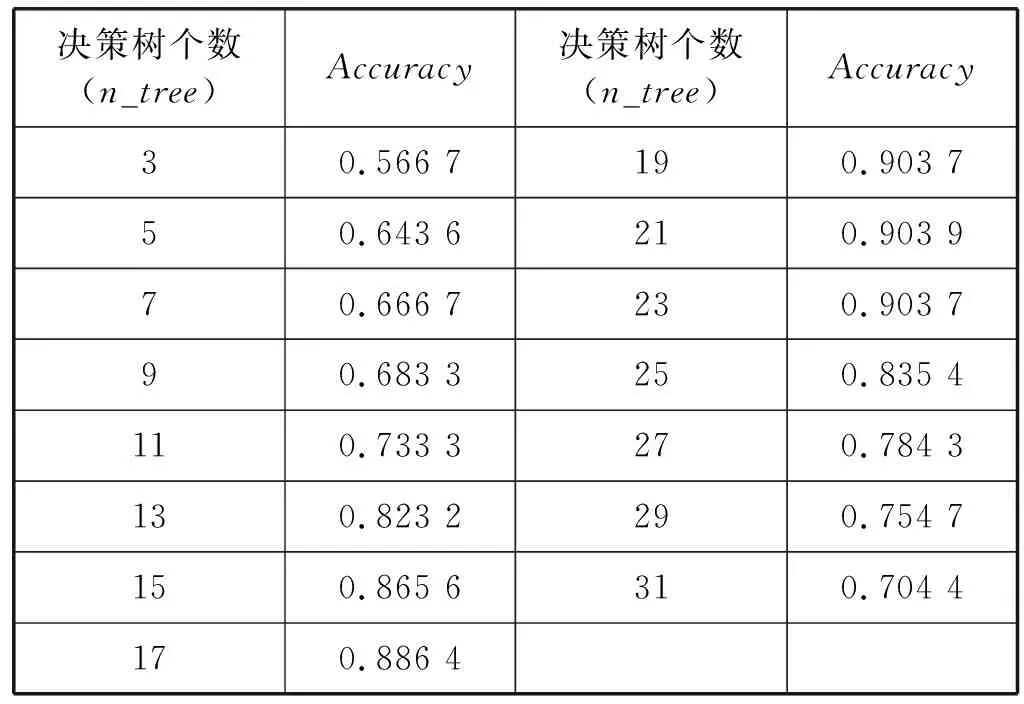
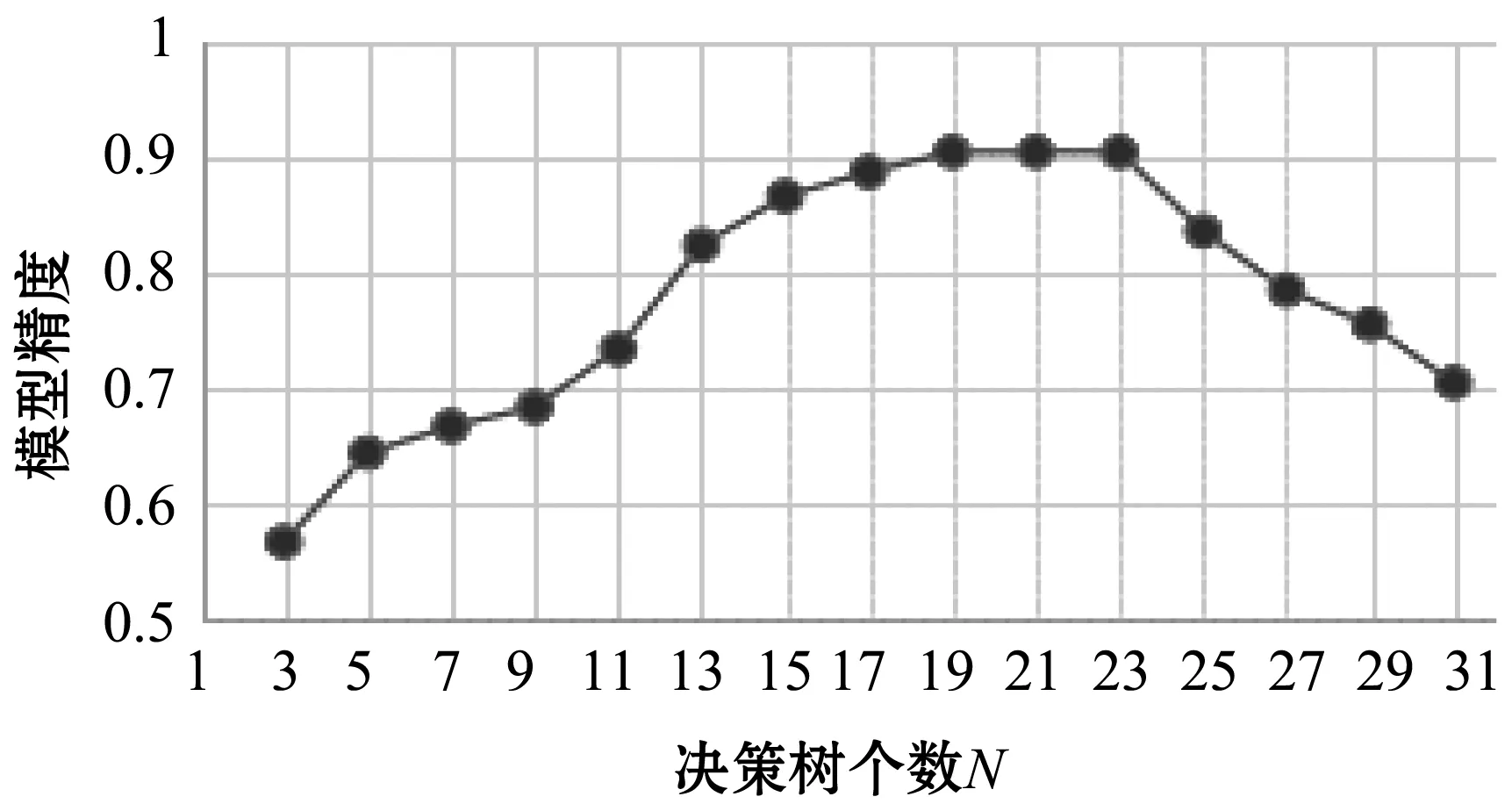
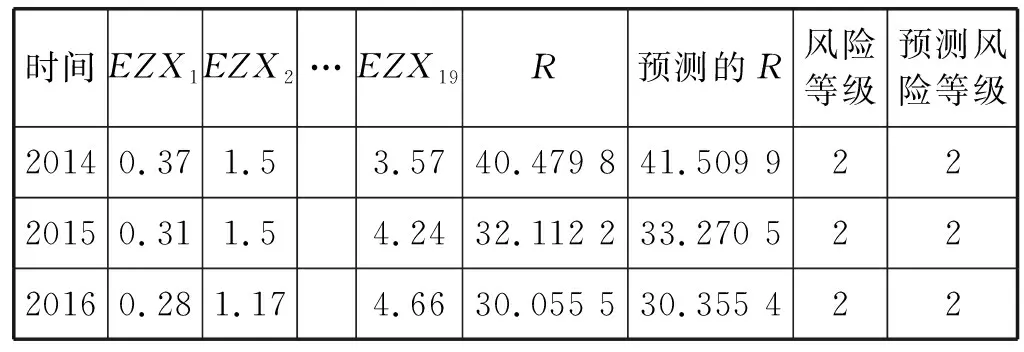
3.5 财政风险预警
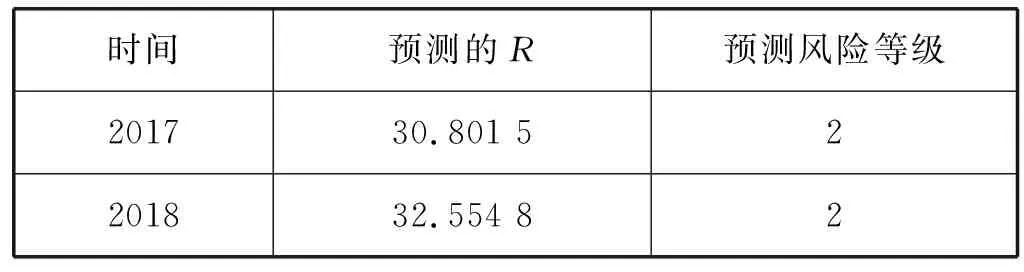
4 结 语
