SIS病毒传播模型在单向网络中的动力学研究
2018-09-26李纪康
李纪康 唐 亮,2 焦 鹏 靖 可
1(沈阳航空航天大学机电工程学院 辽宁 沈阳 110000)2(大连海事大学交通运输管理学院 辽宁 大连 116000)
0 引 言

目前,国内外学者已逐渐开始关注特定传播模型下的动力学特性,并且致力于丰富该领域的理论研究中。文献[15]研究了传播媒介对病毒传播过程中的模型,提出了一种新型的SIS传播模型。文献[16]通过平均场方法研究在社会网络上的病毒传播动力学行为,推导出传播阈值公式,发现传播阈值与模块化系数呈负相关关系。文献[17]将SIS病毒传播模型引入到供应链风险传播研究中,建立了供应链网络风险传播模型。结果表明,当风险传播概率小于风险传播阈值时,供应链网络可以吸收风险。当风险传播概率大于风险传播阈值时,供应链网络将会受到风险影响。文献[18]研究在复杂网络中,节点具有感染方向的新型SIS模型动力学特性。用时滞来描述带有方向感染过程中节点的状态,运用平均场函数理论求出传播的临界值,运用数学分析方法验证网络稳定性。结果表明,传播临界值与实质因素无关。Xu等[19]基于SIS模型的随机微分方程,提出了一种新型的随机临界值理论。文献[20]研究在非线性发生率情况下,一系列随机SIS病毒模型中病毒的持续和消弭。结果表明,临界值对病毒的持续和消弭产生重要的影响。文献[21]研究在非线性发生率和周期系数情况下的,随机SIS病毒模型的动力学行为,运用了Khasminskill的边界周期马尔科夫过程,模型的随机周期解的存在性得到了求证。
以上文献研究了SIS病毒传播模型在无向网络中的传播动力学行为,然而对SIS病毒传播模型在有向网络中传播动力学的研究相对较少。本文研究SIS病毒传播模型在单向规则网络中的传播动力学行为,规则网络选取ER随机网络,网络规模为n。运用数学语言和简单的图形描述病毒在网络中的传播,运用平均场理论得出病毒传播的理论模型,运用数学方法求得病毒的临界值,临界值与出度的平均度呈反比例关系。传播临界值与病毒的传播概率呈正比例关系与恢复概率呈正比例关系。恢复临界值与传播概率和出度平均度呈正比例关系。
1 模型描述
1.1 感染过程数学描述

表1 符号说明
Step1网络选取ER随机网络,出度平均度〈k〉out,网络规模为n,感染概率为λ,恢复概率为δ。初始感染节点为i,出度为ki,初始感染密度ρk(0)=0。
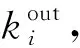
Step3当传播时间为t时,网络中初始感染节点的密度为ρk(t-1),此阶段感染节点密度为(1-δ)ρk(t-1)+λ〈k〉out(1-ρk(t-1))ρk(t-1)。此阶段恢复为易感状态的节点密度为δρk(t),此时处于感染状态的节点密度为(1-δ)ρk(t-1)+λ〈k〉out(1-ρk(t-1))ρk(t-1)-δρk(t)。
Step4当t→∞时,网络的稳态感染密度为ρ*,此阶段属于感染状态的节点数为(1-δ)ρ*+λ〈k〉out(1-ρ*)ρ*。感染节点以δ的概率恢复为易感状态,此阶段恢复为易感状态的节点密度为δρ*。此时处于感染状态的节点密度为(1-δ)ρ*+λ〈k〉out(1-ρ*)ρ*-δρ*。
1.2 感染过程图形描述

图1 感染过程实例描述

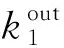
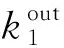
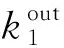
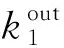
Step5节点1和3处于感染状态,节点4和5恢复为易感状态。该阶段处于感染状态的节点为1、3。节点2和5的感染概率都为λ,感染节点1和3的恢复概都为δ。
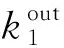
Step7节点3恢复为易感状态,网络中所有节点全部处于易感状态。此时网络处于稳定状态。
2 理论模型构建
由感染模型中的数学描述可以得到如下节点传播的递推式,模型中节点出度为k,在t+1时刻节点感染密度即可表示为:
ρk(t+1)=(1-δ)ρk(t)+λ〈k〉out(1-ρk(t))ρk(t)
(1)
在网络传播达到稳定状态情况时,节点出度为k时的感染密度可表示为:
(2)
ρ*=(1-δ)ρ*+λ〈k〉out(1-ρ*)ρ*
(3)
对式(3)进行处理可以得到:
(4)
理论分析结果表明,病毒在单向网络中同样存在临界值,传播临界值与网络的出度平均度和恢复概率有关。理论分析结果概括如下:
结论1:当恢复概率δ为定值时,传播临界值λc与网络的出度平均度呈反比例关系。
结论2:当网络的出度的平均度为定值时,发生临界现象时的传播概率和恢复概率呈线性关系。当恢复概率δ为1时,即感染节点完全恢复时,临界值为:
理论分析结果表明,即使感染节点完全恢复,网络同样存在临界现象。
结论3:当恢复概率δ为1时,传播临界值只与网络的出度的平均度有关,并且与出度平均度呈反比例关系。
对式(3)进行处理可以得到:
δ=λ〈k〉out(1-ρ*)
(5)
δc=λ〈k〉out
理论分析结果表明,恢复临界值与网络的出度平均度和传播概率有关。理论分析结果概括如下:
结论4:当传播概率λ为定值时,恢复临界值与网路的出度平均度呈正比例关系。
结论5:当网络的出度的平均度为定值时,发生临界现象时的传播概率和恢复概率呈线性关系。
3 传播临界值仿真分析
为了验证上述理论分析的结论和相应的分析结果,本文采用VB语言进行数值仿真,仿真结果主要侧重于相关因素对临界值的影响程度。仿真实验所用ER随机网络均为随机产生,仿真结果为多次仿真结果的平均值,并且随着仿真的进行,网络的结构也会发生相应的调整。

首先研究,当恢复概率δ为定值,网络稳态感染密度ρ*和传播概率λ的关系。模型中的参数取值为:恢复概率δ=0.8,出度的平均度〈k〉out=3和〈k〉out=4,初始感染密度为ρ0=0.001、ρ0=0.005、ρ0=0.01。在以上参数取值情况下,对网络进多次仿真,仿真结果如图2所示。

图2 恢复概率为定值时,稳态感染密度和传播概率的关系
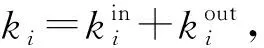
其次研究,网传播概率λ为定值,网络稳态感染密度ρ*和恢复概率δ的关系。模型中的参数取值为:传播概率λ=0.2,出度的平均度〈k〉out=3和〈k〉out=4,初始感染密度为ρ0=0.001、ρ0=0.005、ρ0=0.01。在以上参数取值情况下,对网络进行多次仿真,仿真结果如图3所示。
由图3可得,病毒传播不仅存在临界现象,而且恢复临界值存在一定的规律。网络的初始感染密度不同时,临界值有所不同,随着初始感染密度ρ0的增大,网络临界值逐渐增大。即使初始感染密度不同,当恢复概率δ=0时,网络的稳态感染密度趋于相同值,网络处于稳态下节点基本全部发生感染。由图3可得,出度的平均度〈k〉out越大,临界值越大。实验结果表明,当传播概率λ为定值时,恢复临界值与出度平均度呈现正比例关系,与结论2基本一致。在同种网络中,即使初始感染有所密度不同,但是伴随着恢复概率的增大,稳态感染密度的值都趋于相同值。在初度平均度不同的网络,随着恢复概率的不断变小,网络的稳态感染密度趋于相同值。伴随恢复概率的增大,不同网络稳态感染密度的差别逐渐增大。
接着研究,网络恢复概率δ=1时,即感染节点全部恢复情况下,网络稳态感染密度ρ*和传播概率λ的关系。模型中的参数取值为:恢复概率δ=1,出度的平均度〈k〉out=3和〈k〉out=4,初始感染密度为ρ0=0.001、ρ0=0.005、ρ0=0.01。在以上参数取值情况下,对网络进行多次仿真,仿真结果如图4所示。
由图4可得,即使恢复概率δ=1,网络依然存在临界现象,并且临界值存在一定的规律。网络的在初始感染密度不同时,临界值有所不同,随着初始感染密度ρ0的增大,网络传播临界值的逐渐变小。当传播概率大于临界值时,稳态感染密度由0急剧上升,但是随着传播概率的逐渐增大,网络稳态感染密度增长较为缓慢。即使初始感染密度不同,随着传播概率的增大,稳态感染密度趋于相同值。随着传播概率的增大,稳态感染密度趋于相同值。随着网络出度平均度〈k〉out的增大,传播临界值逐渐减小。当传播概率λ=1时,稳态密度下网络有近半的节点发生感染。实验结果表明,当恢复概率δ为1时,临界值与出度平均度有关,临界值与出度平均度呈反比例关系,与结论3基本一致。
最后研究,当网络发生临界现象时,临界值的理论值和仿真值之间的关系。模型中的参数取值为:出度的平均度〈k〉out=4,初始感染密度为ρ0=0.001、ρ0=0.005、ρ0=0.01、ρ0=0.5、ρ0=1。在以上参数取值情况下,对网络进行多次仿真,仿真结果如图5所示。
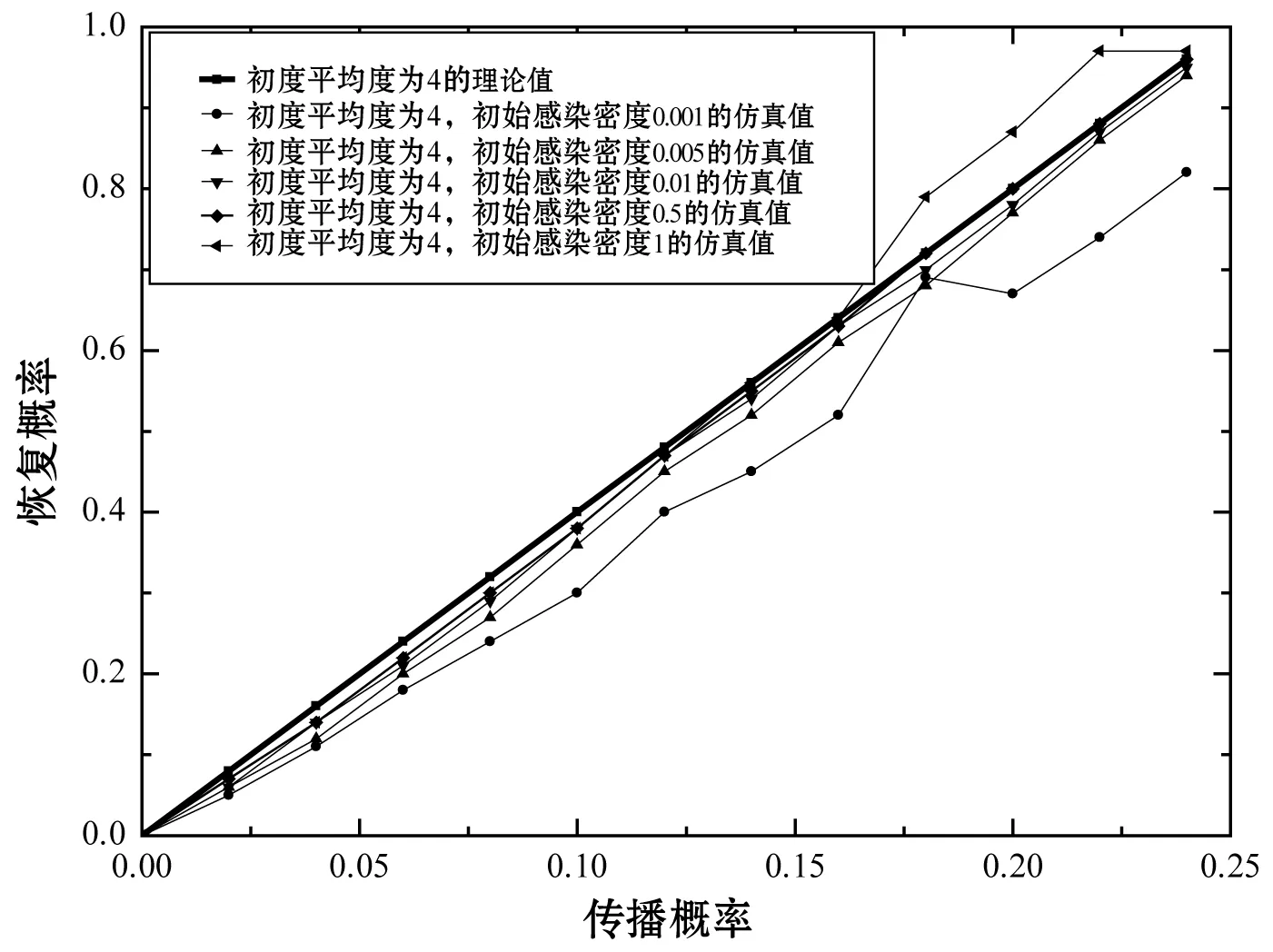
图5 出度平均度为4时,理论值和仿真值之间的关系
图中加粗的直线为临界值的理论值,在初始感染密度不同时,网络临界值的仿真值也有所不同,每组的仿真值都是随着传播概率的增大而进行线性增长。当初始感染密度ρ0=0.001时,在此情况下,临界值的仿真值和理论值之间具有较大的误差。当初始感染密度ρ0=0.5时,临界值的仿真值于理论值误差最小,并且随着传播概率的增大,临界值的仿真值与理论值之间的误差越来越小。当初始感染密度ρ0=1,传播概率λ<0.15时,临界值的仿真值与理论值误差较小,当λ>0.15时,临界值的仿真值不仅超过了理论值,并且随着传播概率的增大,临界值与理论值的误差值逐渐增大。当网络的出度平均度〈k〉out为定值时,发生临界现象时的传播概率与恢复概率呈线性关系,与结论4和5结论基本一致。
由图2-图5可以看出,在特定的情况下,病毒在单向网络中传播,总会存在临界现象。并且发现发生临界现象时的传播临界值和恢复临界值与网络的初度平均度呈线性关系。理论分析的五个结论在仿真分析中均得到了有效的验证。除此之外,从四个图的仿真结果还显示,在同种网络中临界值也会存在差异,并且网络趋于吸收相态时的速率有很大的差别。在不同网络中,网络临界值与初度平均度和初始感染密度有关。最后实验的仿真值和理论值之间的关系图显示,理论值和仿真值存在一定的误差,并且在初始感染密度趋于某些值时,误差可以得到有效控制。
4 结 语
基于SIS病毒传播模型的网络传播过程中,临界值与网络平均度密切相关。理论分析表明,当传播概率为定值时,网络的恢复临界值与网络的出度平均度呈正比例关系。并且发生临界现象时,传播概率和恢复概率呈线性关系。恢复概率为定值时,网络传播临界值与网络的出度平均度呈反比例关系。恢复概率为1时,传播临界值与初度平均度同样呈反比例关系。研究结果表明,单向网络的临界值同样存在,并且与单向网络的出度平均度相关。传播临界值随着出度平均度的线性增加而减小。当恢复概率和出度平均度为定值时,随着初始感染密度的线性增大,临界值的仿真值也呈线性增长的趋势。相反,当传播概率和出度平均度为定值时,临界值的仿真值也随着初始感染密度的变化而变化。随着初始感染密度的增加,临界值的仿真值与理论值之间的误差逐渐缩小。本文提出了基于SIS病毒传播模型的单向网络传播模型,利用简单的数学和图形描述来刻画病毒在单向网络中的传播过程,利用平均场理论研究该模型在均匀单向网络中的传播动力学行为。实验验证了理论分析的五个结论,本文只考虑了均匀单向网络,在实际生活中大多网络是无标度网络。未来会对单向无标度网络进行进一步的详细研究,以丰富复杂网络临界值的研究。
