平面变形回弹迭代补偿的收敛准则及应用
2018-09-22王春鸽翟瑞雪
马 瑞 王春鸽 赵 军 翟瑞雪
1.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,066004 2.燕山大学机械工程学院,秦皇岛,066004 3.浙江大学宁波理工学院机电与能源工程学院,宁波,315100
0 引言
板料成形过程中弹性变形的存在,导致回弹不可避免,而板料成形领域的学者对回弹问题的研究也从未止步。为了实现回弹的有效控制,工程上一般采用工艺控制和模面补偿控制两种方法。工艺控制法是通过调节压边力、凸模行程等参数[1⁃2],改变加载方式[3⁃4],增加成形步骤[5⁃6],提高成形温度[7⁃8]等方式控制回弹,将其限制在工程允许范围内。工艺控制可以在一定程度上减小回弹,但不能彻底消除。因此,对于高精度要求的冲压件,需根据预测值在回弹反方向对模面施加一定补偿量,使回弹后工件满足设计要求,此即为模面补偿控制法。
工程应用中多是通过反复试压和修模,不断改变补偿量,这种方式难以确定补偿量和补偿方向,需花费大量的人力和物力。伴随计算机科学的发展,基于数值模拟分析的半解析有限元法大大提高了回弹控制的补偿效率。针对回弹补偿算法的研究中,应力表述法(force descriptor meth⁃od,FDM)[9⁃10]和位移调整法(displacement adjust⁃ment method,DA)[11]得到学者的广泛认可。以此为基础,为了优化补偿方向、光顺补偿曲面和提高迭代速度,许多改进的补偿算法被陆续提出,如SDA(smooth displacement adjustment)算 法[12]、AC(accelerated compensation)算 法[13]、SGD(shape global deformation)算法[14]、CC(compre⁃hensive compensation)算法[15⁃16]、E-DA(enhanced displacement adjustment)算 法[17]、DCA(discrete curvature adjustment)算 法[18]、CATIA-SGCS(CATIA springback geometry compensation sys⁃tem)系统[19]以及 SEC(sheet elements compensa⁃tion)算法[20]等。
上述改进的FDM算法或DA算法均基于有限元法,将模面单元节点的应力或坐标作为迭代参量,并引入补偿因子进行回弹控制。有限元法是公认的解决工程问题的有效方法,但是其精度依赖于材料模型、单元类型、边界条件等参数的选择,存在反复试错、因人而异的现象,而且采用补偿因子进行定量和定向补偿,无法保证控制参数的收敛性。理论解析可以对迭代参量的变化趋势进行有效分析,但仍无法建立精确计算模型。此外,借助物理试验可以确定当前步迭代参量与目标值的误差,却无法确定下一步的补偿量。为此,本文从数学分析的角度提出了迭代补偿算法,建立了迭代参量收敛性的判定准则,对简单应力状态下和V形自由弯曲工艺中控制参量的收敛性进行了解析证明,并通过宽板V形弯曲实验进行了迭代补偿应用研究。
1 基于简单迭代法的迭代补偿机制
1.1 简单迭代法的引入
在讨论影响回弹的因素时,王允禧[21]明确指出,“弯曲中心角α愈大,则变形区的长度愈大,弹复积累也愈大,故弹复角Δφ也愈大”。肖景容等[22]也强调,“弯曲角α愈大,则在总变形中的弹性变形所占的比例会相应增大,回弹值Δα也愈大”。此外,由图1所示的弹塑性变形回弹过程中的等效应力应变关系可知,较大等效应变量εˉ2产生的回弹量明显大于较小等效应变量 εˉ1产生的回弹量因此,对于普通金属材料,在变形条件不改变的前提下,变形量越大,回弹量越大,这也是本文的理论基础。

图1 回弹过程中的等效应力应变关系曲线Fig.1 Equivalent stress-strain curve in elastic-plastic deformation and springback process
设x为控制参量回弹前的值,f(x)为控制参量回弹前后的函数关系,则回弹量可以表示为

根据上述理论基础,如果Δ(x)为单调增函数,即Δ′(x)> 0,则有

回弹控制的目的是确定一个回弹前的值a,使其回弹后为ap,也就是求解方程

为此,引入简单迭代法[23],按照其求根思想,构造迭代方程

又由式(2)可知

由简单迭代法的局部收敛定理可知,迭代方程(4)是收敛的,即存在x*满足x*=φ(x*)。如图2所示,取初值为ap,按照迭代方程得到迭代序列:

对于预先设定的误差e,当 |xk-xk-1|≤e时,认为x*≈xk,同时有f(x*)-ap=0,即为所求。

对于回弹控制问题,构造回弹前后参量的关系函数y=f(x),若满足f′(x)< 1,则可以采用迭代补偿法使控制参量收敛到目标值。因此,对于回弹问题的补偿计算,f′(x)<1可作为所选参量收敛性的判定准则,且此种收敛方式适用于弯曲回弹后变小的参量,如曲率K、弯曲角α。
目前所有回弹问题的理论解析方法皆不能建立精确计算模型,但理论解析对参量变化趋势的预测是可信的;试验方法虽然能给出与目标量的误差,但没有理论指导确定下一步的补偿量。本文的迭代补偿是基于理论解析f′(x)<1判定迭代收敛,再基于每次试验的回弹量确定下一次的补偿量。
1.2 回弹控制的迭代补偿机制
对于一般的回弹问题,难以建立1.1节中回弹前后参量值的函数关系式y=f(x),因此,本文基于简单迭代法建立了通用回弹问题的迭代补偿算法。回弹控制的迭代补偿机制描述如下:对于一般冲压工艺的回弹问题,确定一个工艺参数,该值具有回弹后值比回弹前值小的特点,并能够根据局部收敛定理证明其迭代收敛性,即可基于迭代补偿算法,对该参量按照一定的精度要求进行有限次补偿操作,使其逐渐逼近所需目标值。
如图3所示,确定迭代工艺参数的收敛性后,欲使工件回弹后的参数值为ap,确定回弹前的值(即模面形状参数a)的迭代法流程如下:
(1)准备。确定初值,一般选为目标值x0=ap。
(2)迭代。进行工艺操作,获得回弹后值x1。
(3)控制。检查x1-ap:若 |x1-ap|≤ e(e为预先指定的成形件尺寸精度),则终止迭代,且有a=x0;否则,将 | x1-ap|作为补偿量,令x0=x1+ | x1-ap|,转步骤(2),继续迭代。
(4)输出。当 | x1-ap|≤e时终止迭代,a=x0,即最终模面参数值。

图3 回弹控制的迭代补偿流程图Fig.3 Iterative compensation process for springback control
上述补偿流程表明,运用迭代补偿机制可以从数学分析的角度对回弹问题补偿控制的正确性提供理论依据。同时,基于迭代补偿机制,根据每次试验的回弹量可以预测下一次补偿值,提高收敛速度。而且,对于同一材料的同一成形工艺,该补偿值只取决于迭代参量回弹前后的差值,因此,该机制的通用性很高。
2 简单应力状态下的迭代收敛性证明
简单应力状态下,假设材料符合双线性硬化模型为
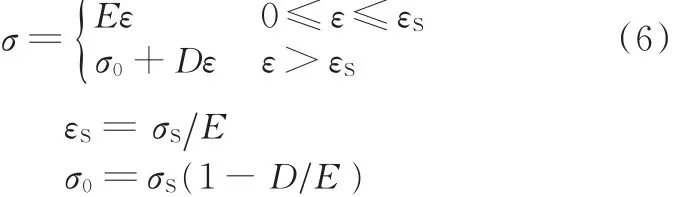
式中,σ为应力;ε为应变;E为弹性模量;D为塑性切线模量;σS为屈服极限。
2.1 平板单向拉伸
受单向拉伸的平板见图4,整个工件处于单向应力状态。设平板的初始长度为l0,加载结束后长度为l,卸载后长度为l′,σT为拉伸结束时的截面应力。

图4 平板单向拉伸Fig.4 Flat uniaxial stretching
由双线性应力应变关系式可知,截面应变
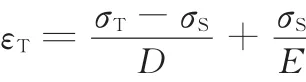
卸载后板料长度
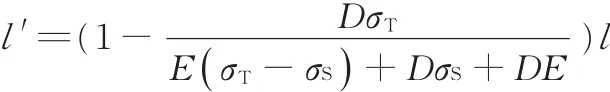
对上式求导,可得
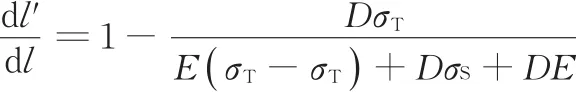

即

由式(2)所示回弹问题迭代参量收敛性的判定准则可知,板材单向弹塑性拉伸变形中,轴向长度可作为迭代控制参数进行回弹控制。
2.2 平板双向拉伸
受双向拉伸的平板处于平面应力状态见图5。假设加载方式为简单加载,σ1方向为主应力方向,初始长度为l10,加载结束后长度为l1,卸载后长度为l′1;σ2方向为次应力方向,初始长度为l20,加载结束后长度为l2,卸载后长度为l′2。
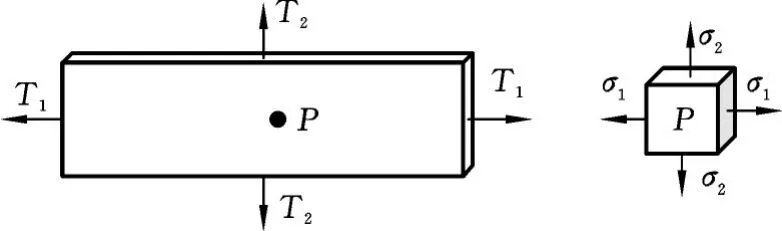
图5 平板双向拉伸Fig.5 Flat biaxial stretching
定义α和β分别为应力比和应变比,且满足

其中,σ1为主应力,σ2为次应力,ε1为主应变,ε2为次应变。显然,α<1,β<1。
又由真实应变(对数应变)定义可知
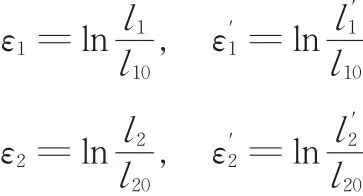
根据经典卸载理论,卸载回弹部分的应变

又由广义胡克定律可知

式中,υ为泊松比。
根据体积不变条件,等效应变εˉ和残余等效应变 εˉ′可分别表示为
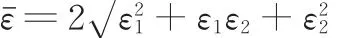
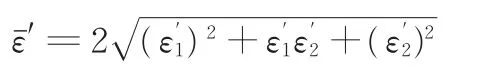
又由双线性材料模型可知,等效应力应变满足
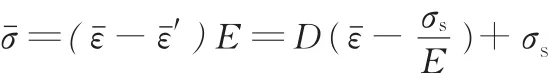
令

则有
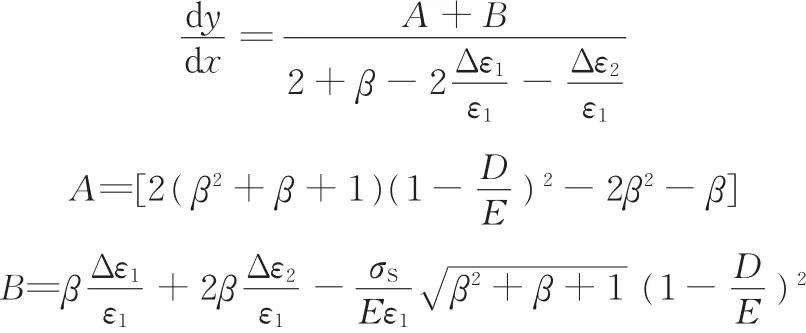
在 一 般 的 塑 形 变 形 中 ,因 为 ε1≫ Δε1,ε1≫ Δε2,所以

对于一般金属材料,E≫D,故(1-D E)2≈ 1,所以
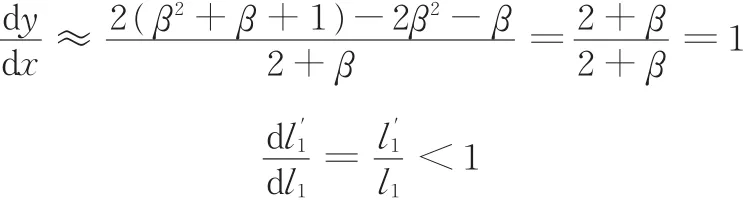
由式(2)所示回弹问题迭代参量收敛性的判定准则可知,x向轴向长度可作为迭代控制参数进行回弹控制。同理,选取y向长度也可以证明轴向长度的收敛性。因此,在板材双向弹塑性拉伸变形中,轴向长度对于迭代补偿机制具有收敛性,可以进行补偿计算。
3 V形自由弯曲的迭代收敛性证明
矩形截面板在弯矩M的作用下发生自由弯曲,并在卸载后发生回弹,回弹前后的几何关系见图6。现设定如下:弯曲后,板料中性层的弯曲半径为ρ,曲率为K,弯曲角为α,弯角(即弯曲角的补交)为β;回弹后,板料中性层的弯曲半径为ρp,曲率为Kp,弯曲角为 αp,弯角为 βp;回弹角为 Δα,曲率回弹量为ΔK。
显然,在工程实际中,有:0 < ρ< ρp,K=1 ρ,Kp=1 ρp,则0<Kp<K;π≥ α> αp≥ 0,β=π-α,βp=π-αp,故 0≤β<βp≤π;Δα=
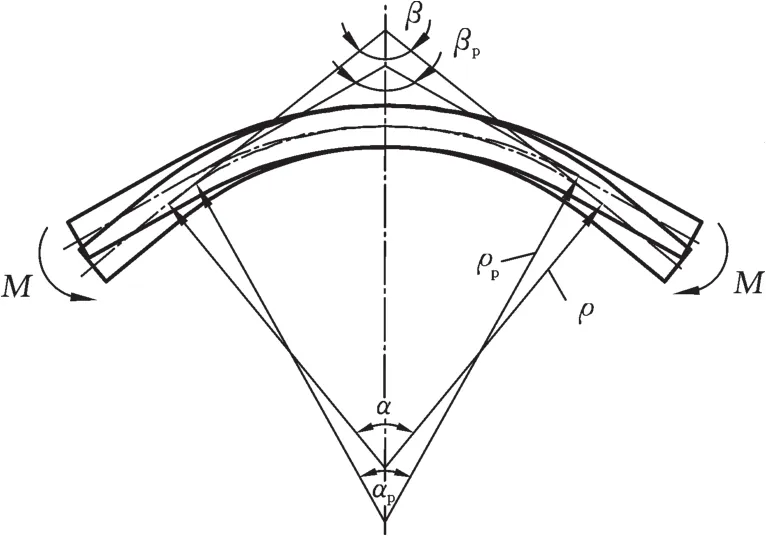
图6 板料弯曲回弹前后的几何关系Fig.6 Geometrical relationship before and after springback
弹塑性弯曲过程中,曲率回弹量[22]
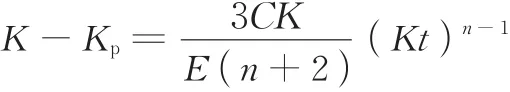
其中,C、n均为与材料性质有关的常数,通常由实验得出;t为板厚。将上式对K求导,可得

同时,弯曲角回弹量[22]
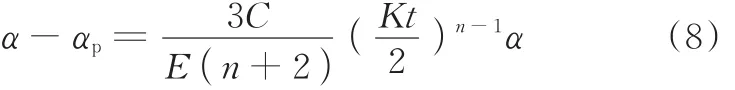
将上式对α求导,可得
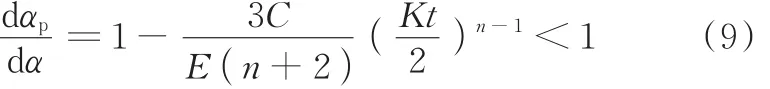
由式(7)和式(9)可知,曲率和弯曲角满足式(2)所示迭代参量收敛性的判定准则。因此,在V形自由弯曲工艺中,板料曲率K和弯曲角α均可作为迭代控制参数进行补偿计算。
4 迭代补偿机制的应用研究
4.1 实验方案
为了研究迭代补偿机制的应用情况,对V形自由弯曲工艺分别进行曲率迭代补偿控制工艺实验和弯曲角迭代补偿控制工艺实验。实验模具安装在WDD-LCT-150型电子拉扭组合多功能试验机上,其位移控制精度为0.01 mm。采用美国星科(CimCore)公司生产的3000iTM系列便携式三坐标测量仪测量弯曲板坯的形状,测量精度为0.01 mm。
图7a中,曲率迭代补偿控制工艺实验模具主要由上模、下模和调整垫片组成,下模圆角半径r2为25 mm,两圆角中心距L为100 mm。弯曲上模有3个,半径分别为60 mm、80 mm和113.33 mm。图7a中垫片为平均厚度为0.08 mm的中硬铝簿,与凸模组合,形成等效上模,实现弯曲半径的微段变动。弯曲角迭代补偿控制工艺实验模具与曲率补偿实验共用一套下模,上模为半径为33.33 mm的半圆形冲头,见图7b。

图7 迭代补偿实验模具Fig.7 Iterative compensation experiment of V-free bending
实验板料为SS400钢板,其几何尺寸及材料性能参数见表1。实际上,本文提出的迭代补偿机制不依赖材料特性,表1只是为了给出实验材料的相关信息。

表1 实验用SS400钢板的几何尺寸及材料性能参数Tab.1 Geometrical dimensions and material properties of SS400 steel sheet
曲率迭代补偿控制工艺实验包括以下两组:①曲率收敛性证明实验。采用“弯曲模+垫片”组合,得到弯曲半径ρ分别为60 mm、68 mm、80 mm、90 mm和113.33 mm的“等效上模”,对板坯进行加载,并对回弹前后的弯曲曲率进行测量统计,分析其收敛性。②曲率迭代补偿工艺实验。确定误差精度为0.1%,按照上文提出的迭代补偿算法,分别进行目标弯曲半径ρd为70 mm和95 mm的迭代补偿实验。为了便于实验数据的测量,试验过程中对弯曲半径ρ进行控制和测量,并换算为曲率K后进行分析计算。
与曲率迭代补偿控制工艺实验类似,弯曲角迭代补偿控制工艺实验包括以下两组:①弯曲角收敛性证明实验。通过控制上模压下量对板坯进行多组弯曲实验,然后对回弹前后弯曲角进行测量统计,分析其收敛性。②弯曲角迭代补偿工艺实验。目标弯曲角αd分别为30°和60°,误差不大于0.5%。V形自由弯曲过程中,上模与板坯接触的包覆角被近似为弯曲角。因此,由板坯弯曲过程中的几何关系确定的上模压下量S与弯曲角α的关系为
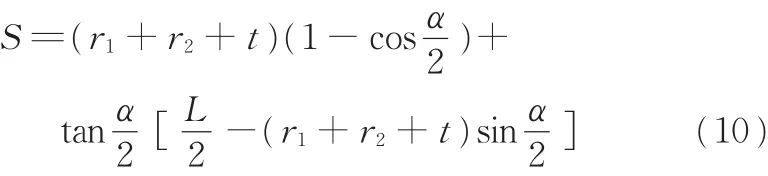
4.2 曲率迭代补偿控制工艺实验结果分析
对实验板料进行不同弯曲半径的加载—卸载实验,见图8,得到回弹前后的中心层曲率,见图9。对板坯弯曲曲率K与回弹后曲率Kp进行拟合,满足关系式Kp=-5.5817K2+1.0419K+10-5。显然,当K>0.003 75 mm-1时,曲线上任意一点的曲率小于1,而且,K越大,斜率越小。因此,由迭代收参量敛性准则可知,曲率可以作为迭代参数进行回弹控制,这也与理论解析的结论一致。
对SS400钢板分别进行目标弯曲半径ρd为70 mm和95 mm的曲率补偿工艺实验,对应曲率分别为1.428 57×10-2mm-1和1.052 63×10-2mm-1,补偿过程见表2。

图8 曲率收敛性证明实验Fig.8 Proof experiment of curvature convergence
以目标弯曲半径ρd为70 mm为例,详述其补偿过程:
(1)确定补偿精度为0.1%,即半径补偿误差小于0.07 mm,曲率误差小于1.43×10-5mm-1;

表2 曲率迭代补偿计算Tab.2 Iterative compensation process of curvature in V-free bending
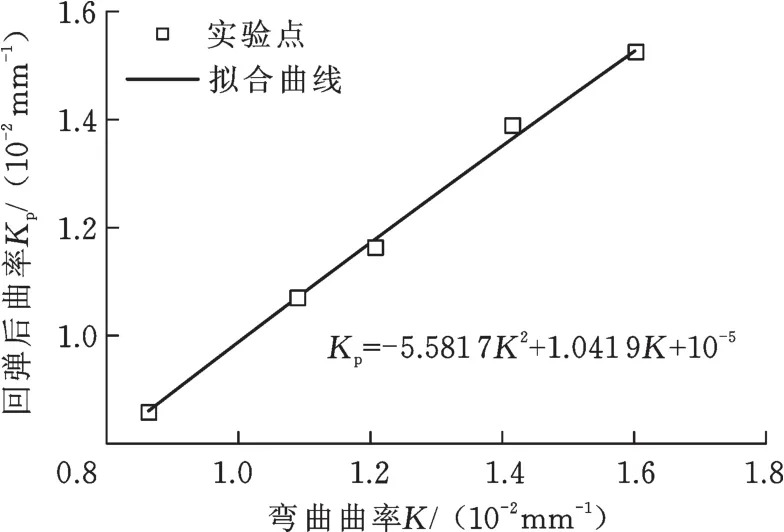
图9 回弹前后的弯曲曲率关系Fig.9 Curvatures of bending parts in V-free bending before and after springback
(2)以目标值作为迭代初值,首次弯曲上模的半径ρ1=70.021mm,待板坯包覆上模后,卸载,测得回弹后弯曲半径=73.072 mm;补偿误差为-Kd|=59.940×10-5mm-1,不满足精度要求,需进行第二次补偿;确定二次弯曲曲率=K(2)+|-Kd|=1488.08 × 10-5mm-1。
通过3次补偿,确定自由弯曲上模半径为67.088 mm时,可获得弯曲半径为70 mm的弯曲件,误差可控制在0.1%以内。由表2可知,随着补偿次数的增加,补偿误差快速减小,迭代参数快速逼近目标值。由此表明,对于自由弯曲工艺,可以将弯曲曲率作为迭代参量,通过有限次迭代补偿确定上模尺寸,获得满足精度要求的成形件。
4.3 弯曲角迭代补偿控制工艺实验结果分析
通过控制压下量对SS400板坯进行多组自由弯曲实验,对回弹前后的弯曲角数据进行拟合,结果见图10。回弹前后弯曲角满足关系式αp=-0.0004α2+1.0122α-1.278。显然,当弯曲角大于20°时,曲线上任意一点的斜率小于1。因此,弯曲角可以作为迭代参数进行迭代补偿控制。

图10 回弹前后的弯曲角关系Fig.10 Bending angles of bending parts in V-free bending before and after springback
对SS400钢板分别进行目标弯角αd为30°和60°的弯曲角迭代补偿工艺实验,补偿过程见表3,其补偿流程与曲率迭代补偿工艺实验类似,不再赘述。由表3可以看出,经过2~3次迭代补偿,就能够获得目标弯曲角,且误差小于0.5%。由此表明,基于迭代补偿算法的回弹控制方法,其回弹量的动态补偿具有稳定的收敛方向,且误差可评估,是具有实用价值的有限次补偿方法。
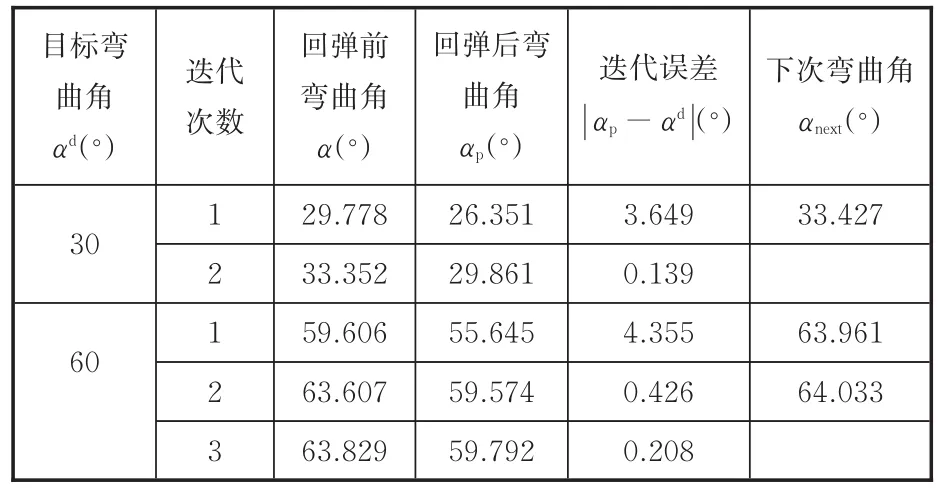
表3 弯曲角迭代补偿计算Tab.3 Iteration compensation calculation of bending angle
5 结论
(1)基于简单迭代法,提出了平面变形回弹控制的迭代补偿机制,该机制不依赖于材料性能和力学模型,更具有实用价值。
(2)基于迭代补偿机制,建立了迭代参量收敛性证明的判定准则,并理论证明了简单应力状态下,轴向长度可以作为迭代参量进行回弹补偿控制。
(3)依据迭代参量收敛性判定准则,理论证明了V形自由弯曲工艺中曲率和弯曲角的迭代收敛性,对回弹控制问题中模具修正方法的正确性提供了本质的理论依据,并完善了实际操作的理论基础。
(4)将迭代补偿机制用于V形弯曲回弹控制,经2~3次迭代,即可获得误差小于0.1%的目标曲率和误差小于0.5%的目标弯曲角,收敛速度很快。
