一种改进的非局部极值FCM图像分割算法

马冬梅，武永娟，火元莲，邹 鑫

(西北师范大学 物理与电子工程学院，甘肃 兰州 730070)

0 引 言

图像分割是图像分析中最艰巨的任务和最具有挑战性的问题之一。其目的是将图像划分为区域或簇，使得同一簇中的像素尽可能相似，而且不同簇中的像素尽可能相异。图像分割用于机器人视觉、地理、对象识别和监控视频分析等各种领域。图像分割方法可以分为基于图论的方法、基于分类的方法和基于聚类的方法[1]。模糊C均值算法(FCM)是一种无监督的聚类算法，目前广泛应用于医学图像[2]、遥感图像[3]和红外图像[4]等多个方面。

FCM算法由Dunn[5]提出并由Bezdek[6]改进建立了FCM算法理论，它是在硬聚类分割的基础上引入模糊性，可以保留图像中更多的信息。FCM算法的主要缺点是：确定聚类中心和聚类数、未考虑空间信息。针对这两个问题，研究者提出了改进的FCM算法。例如，Hemalatha等[7]采用改进的粒子群优化聚类中心，克服了对初始值敏感的问题，但是与传统FCM算法结合，分割效果差；刘万军等[8]首先用图像的灰度直方图确定聚类数，然后使用一种改进的快速FCM方法产生初始聚类中心，解决了自动分割的问题，但是计算复杂度高；Gong等[9]引入了权重加权模糊因子和核函数，增强了FCM算法的抗噪性能和鲁棒性，但聚类中心迭代公式存在理论缺陷，计算复杂度高；胡嘉骏等[10]将图像的邻域灰度信息和隶属度的信息加入算法中，以自动调节算法对噪声的影响，但是未考虑初始值的选取，导致分割结果陷入局部极值。

在上述研究的基础上，文中利用直方图的斜率确定聚类中心和聚类数，解决了对初始值敏感、易陷入局部最优解的问题。采用非局部滤波方法，既能去除噪声也能很好地保持图像细节信息，提高了分割精度。

1 模糊C均值聚类

用于图像分割的FCM聚类算法的基本思想是，通过迭代像素到特征空间中的聚类中心的距离最小化的目标函数来实现，然后，按照最大隶属度准则对像素进行划分，实现图像分割。目标函数定义为：

(1)

其中，c[2,N)为聚类数目；N为像素的总数；m为模糊隶属度上的权重指数；‖xi-vj‖2为第i个像素xi与第j个聚类中心vj之间的欧氏距离；uij为xi相对于vj的模糊隶属度。

式1需要满足的约束条件为：

j=1,2,…,c

(2)

使用拉格朗日乘子法，在约束条件式2下找到目标函数式1的极值，构建拉格朗日函数。通过拉格朗日函数对各个变量求偏导，取得模糊隶属度和聚类中心的迭代公式如下：

(3)

(4)

从式1目标函数得出不包括任何的局部信息，FCM对噪声敏感。为了克服这一问题，Ahmed等[11]通过在像素周围应用正方形窗口来找到每个像素的邻域。该方法的目的是使用局部邻域信息保留图像细节，以增强图像对噪声的鲁棒性。FCM_S算法的目标函数如下：

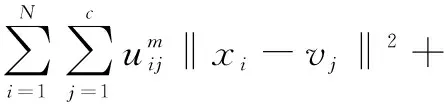
(5)

其中，α(0≤α≤1)为控制邻域空间信息的参数；Ni为像素i落在邻域窗口中的邻域点；NR为邻域点的数量；xr为xi的邻域。

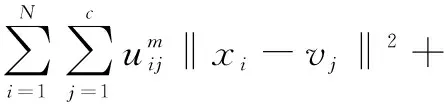
(6)

该算法需要手动设置参数α，对性能有很大的影响。对于不同图像需要设置不同的参数，导致去除噪声和保留图像细节信息都会受到很大影响。Yang和Tsai[13]针对自适应调整α，提出用高斯核函数计算新参数ηj，虽然这个参数改进了结果，但是必须在每次迭代中更新，计算费时。为了解决这个问题，Ahmed等[14]引入了自适应正则化参数和加权滤波方法，来控制每个像素的局部信息。ARKFCM具有三种形式，即均值滤波(ARKFCM1)、中值滤波(ARKFCM2)和加权滤波(ARKFCMw)。因为加权滤波实际上是一种线性滤波，所以在滤波的过程中可能给图像细节造成损失，影响分割精度。而文中的非局部滤波既能去除噪声，也能很好地保持图像细节信息，提高了分割精度。

2 文中算法

首先按照直方图的斜率来确定聚类数和聚类中心，方法如下：

直方图上的某一点p与前一点和后一点的斜率分别为：

Kmp=Kp-1,p×Kp,p+1

其中，xp-1、xp、xp+1分别是直方图中点p前一点、点p以及点p后一点的灰度值；yp-1、yp、yp+1分别是直方图中点p前一点、点p以及点p后一点的频率值。

根据斜率来判断点p是否是聚类中心，判断规则如下：

因此，不能成为聚类中心的点被删除，剩余的就是聚类中心。根据阈值参数，通过计算聚类中心之间的欧几里德距离来限制聚类中心距离差异，以确定最后的聚类中心。

阈值过程定义为：Dji≤T，点p不是聚类中心，其中Dji=‖xpj-xpi‖。

而聚类数最终是由聚类中心决定的(聚类数c=|p|)。

然后计算窗口邻域Ni中像素的相对灰度标准偏差(RSDi)，定义如下：

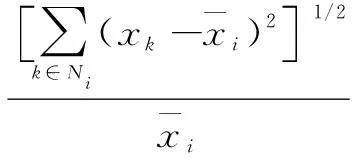
(7)

RSDi应用于指数核函数来求出局部窗口内的权重为：

(8)

将获得的权重归一化为：

(9)

自适应正则化参数γi描述如下：

(10)

通过非局部滤波[15]引入空间信息，非局部滤波像素的权重不单单只与像素点的相似性相关，而且与每个像素点的邻域图像块的相似性相关，对每个像素进行非局部滤波，定义如下：

(11)

(12)

其中，Z(i)为归一化常数，而

(13)

其中，Ni和Nj是以像素i和像素j为中心的正方形邻域；YNi和YNj是两个邻域上所有像素灰度值的邻域向量；参数σ1为控制滤波的平滑程度，根据数据本身的特性确定[16]，定义σ1如下：

(14)

文中使用核函数来代替欧氏距离，核函数就是将图像平面中的输入数据非线性映射到较高维特征空间，在特征空间中，欧氏距离‖ξi-vj‖2被‖Φ(ξi)-Φ(vj)‖2取代，定义为：

‖Φ(ξi)-Φ(vj)‖2=2(1-K(ξi,vj))

(15)

根据文献[17]，文中利用高斯核函数，方法如下：

(16)

其中，σ是核带宽。它的选择仍然是一个问题。文献[9]中，基于所有像素之间的距离方差来计算σ：

(17)

目标函数定义为：

(18)

通过使用拉格朗日乘数法最小化公式，得到新的隶属度uij和聚类中心vj的方程如下：

uij=

(19)

(20)

算法的步骤如下：

步骤1：输入待分割图像；

步骤2：计算图像直方图的斜率，确定聚类数和聚类中心；

步骤3：设置参数，如初始化阈值ε=0.001，m=2，循环计数器t=0；

步骤4：计算非局部均值ξi；

步骤5：计算自适应正则化参数γi；

步骤6：用式19计算隶属度函数uij；

步骤7：用式20计算聚类中心vj；

步骤8：如果max‖u(t+1)-u(t)‖<ε或t>100，则停止；否则，更新t=t+1并转到步骤6；

步骤9：按照隶属度大小，把像素点划分到隶属度最大的那一类，实现聚类分割。

3 实验结果与分析

以给定图像为对象，将该算法的分割结果与现有算法FCM、EnFCM、ARKFCM1、ARKFCM2和ARKFCMw进行比较，以验证算法的有效性。所有实验选择3×3像素的窗口大小，模糊指数m=2，迭代误差ε=0.001，最大迭代次数t=100。使用Jaccard相似度(JS)度量对图像分割精度进行定量分析。JS计算如下：

(21)

其中，S1、S2分别是准确分割结果和需要判断的分割结果。JS越大，分割精度越高。

第一个实验是将具有217×181的T1加权轴向切片7%噪声和20%灰度不均匀的图像进行分割，分割结果和JS、平均运行时间分别如图1和表1所示。

第二个实验是将具有181×217的T1加权矢状切片7%噪声和20%灰度不均匀的图像进行分割，分割结果和JS、平均运行时间分别如图2和表2所示。

图1 T1加权轴向切片图像分割结果

图2 T1加权矢状切片的图像分割结果

指标FCMEnFCMARKFCM1ARKFCM2ARKFCMw文中算法WM(脑白质)0.8960.9330.9400.9410.9400.943GM(脑灰质)0.7950.8510.8640.8680.8650.869CSF(脑脊液)0.8160.8540.8630.8670.8670.867JS0.8350.8790.8890.8920.8910.893时间/s7.120.895.765.655.716.48

表2 T1加权矢状切片的图像分割JS和运行时间

指标FCMEnFCMARKFCM1ARKFCM2ARKFCMw文中算法WM(脑白质)0.7400.7670.7850.7880.7860.789GM(脑灰质)0.7650.7930.8150.8160.8160.816CSF(脑脊液)0.8380.8660.8710.8720.8750.874JS0.7810.8080.8240.8250.8250.826时间/s7.130.855.765.755.786.50

从分割结果可以看出，FCM算法分割出的边界比较模糊而去噪效果差，EnFCM算法分割出的目标和背景中仍然存在很多的噪声点，ARKFCM算法中,ARKFCM2算法的分割效果最好，但是它在保持图像细节方面不准确，运行时间短。而文中算法对噪声和图像细节保持方面有更好的平衡。

4 结束语

通过计算直方图中每个点的斜率来确定聚类中心和聚类数，然后引入非局部滤波计算加权图像。自适应地结合了灰度信息和空间信息，以提高分割精度、增强噪声的鲁棒性。实验结果表明，文中算法比其他5种聚类算法具有更高的JS，并且分割结果在平滑边界和保留图像细节之间具有很好的平衡。但该算法在运行时间上相对较慢，因此，缩短运行时间是进行分割的下一步研究方向。