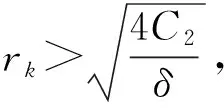一类超二次二阶Hamilton系统的周期解
2018-09-21聂千千
聂千千,郭 飞
(天津大学数学学院,天津 300354)
1 主要结论
本文主要研究二阶非自治Hamilton系统
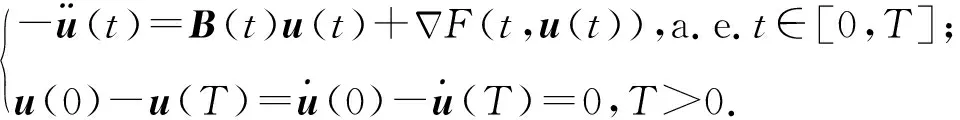
(1)

Hamilton系统周期解的存在性问题由Rabinowitz[1]于1978年解决,此后许多文献应用临界点理论和变分法对Hamilton系统周期解的存在性和多重性进行了深入研究.其中有很多文献考虑了形如(1)式的系统:在原点附近时,系统的动态行为主要由矩阵函数B(t)主导,但随着|x|的增加,能量函数F超二次增长并占据主导地位.李树杰[2]在矩阵函数B(t)是常值对称矩阵、F满足经典超二次条件下得到了系统周期解的存在性.随后李树杰和Willem[3]推广了上述结论,研究了矩阵函数B(t)为连续函数矩阵的条件下系统周期解的存在性.2014年,Pipan等[4]讨论了系统(1)在矩阵函数B(t)的元素仅是L1可积的情况下周期解的存在性问题.2016年,李林等[5]研究系统(1)时令函数F(t,u)满足下列条件:



其中λl-1和λl将在本文的第2部分介绍.在这些假设条件下,文献[5]证明了系统 (1)至少有一个T-周期解,若进一步假设F(t,-u)=F(t,u),则证明了系统(1)有无穷多个T-周期解,结果如下:
定理1.1[5]假设函数F满足条件(F1)—(F3),则系统(1)至少有一个T-周期解,且它的二阶弱导数L1可积.
定理1.2[5]假设函数F(t,u)关于u是偶的,满足条件(F1)—(F2),则系统(1)有无穷多个T-周期解,且它们的二阶弱导数L1可积.
本文将条件(F2)进行了如下推广:
(F2′) 存在常数α>0,R>0,使得
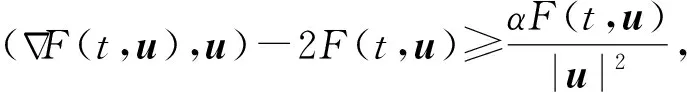
该条件由唐春雷等[6]提出,本文用这一推广的条件得到了如下更为一般的结论:
定理1.3假设函数F满足条件(F1),(F2′),(F3),则系统(1)至少有一个T-周期的弱解.
定理1.4假设函数F(t,u)关于u是偶的,且满足条件(F1)与(F2′),则系统(1)有无穷多个T-周期的弱解.
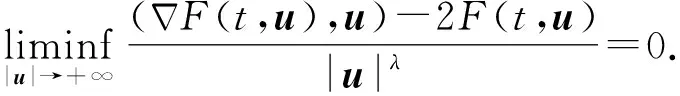
2 预备知识
在空间L2([0,T],RN)×L2([0,T],RN)上定义如下的双线性型a(·,·)和b(·,·):
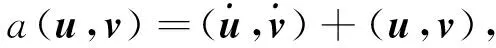
b(u,v)=-((B(t)+IN)u(t),v(t))dt.
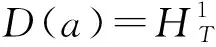
(2)
由文献 [5] 的结论知
(3)
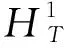
定义双线性型d(u,v)=a(u,v)+b(u,v),有如下引理:


d(u,u)>δ‖u‖2,u∈H+.
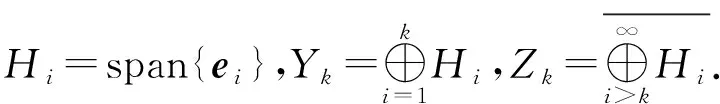
定义2.1[7]设E是实Banach空间,泛函φ∈C1(E,R).若序列{un}⊂E,{φ(un)}有界和‖φ′(un)‖(1+‖un‖)→0蕴含{un}有收敛子列,则称泛函φ满足Cerami条件,简称(C)条件.
引理2.2[5](环绕定理) 设E是实Banach空间,泛函φ∈C1(E,R),A,B是E的两个子集满足A与B环绕,且

假若泛函φ满足(C)条件,则泛函φ有一个临界点.
引理2.3[8](喷泉定理) 假设泛函φ∈C1(E,R)满足(C)条件.对于任意k∈N,存在ρk>rk>0使得:
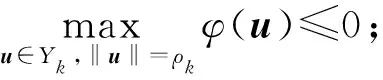

其中Yk和Zk如上述定义.则泛函φ有一列趋于正无穷的临界值序列.
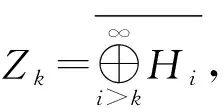
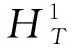
3 主要结果的证明


引理3.2假设条件(F1)和(F2′)成立,则泛函φ满足(C)条件.

|φ(un)|≤M,‖φ′(un)‖(1+‖un‖)≤M,∀n∈N*.
为了证明{un}有收敛子列,首先用反证法证明{un}有界,证明的想法来自文献[6].
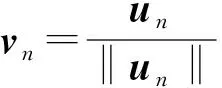
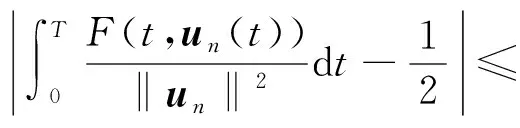
(4)
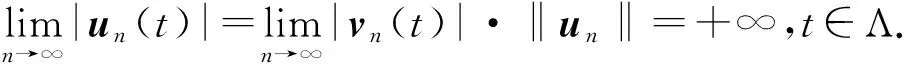
(5)
又由条件(F1)知存在常数R1>R>0使得
F(t,u)≥0,∀u∈RN且|u|>R1,t∈[0,T].
(6)
因为函数F(t,u)连续可微,故存在常数C>0,使得
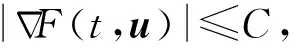
(7)
由(6)—(7)式,
F(t,u)≥-C,∀u∈RN,t∈[0,T].
(8)
再由Fatou引理以及(5)和(8)式,
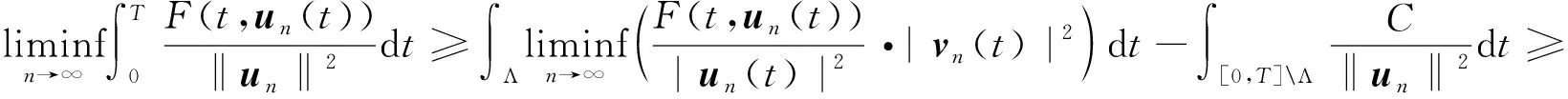
这与(4)式矛盾.
若v≡0,则由(4)式得
(9)
令Ωn={t∈[0,T]||un(t)|>R1},由(7)式以及条件(F2′),




可得‖un-u‖→0(n→∞).这就证明了引理3.2.
定理1.3的证明
证明由引理3.1和引理3.2,泛函φ满足引理2.2的所有假设,从而系统(1)至少有一个T-周期的弱解.
定理1.4的证明
证明借助引理2.3来证明.显然,泛函φ是偶的.引理3.2说明泛函φ满足(C)条件,因此为了证明定理1.2,只需证明引理2.3中的条件(A1)和(A2)成立.

-F(t,u)≤-(1+CB)M1|u|2+C1,∀u∈RN,t∈[0,T],
(10)
其中C1是常数.故对任意u∈Yk,由(3)和(10)式,

(11)
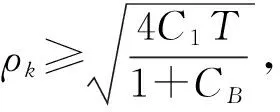
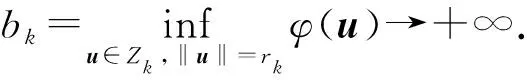
(12)