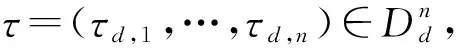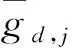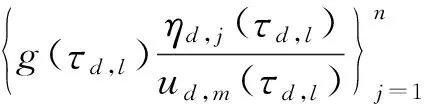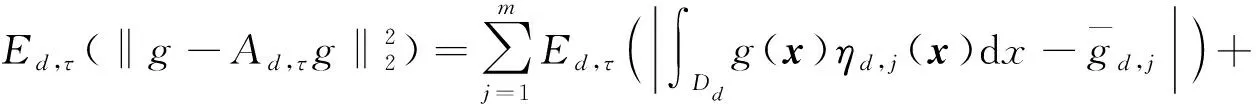平均框架下Korobov空间的逼近基于标准信息的易处理性

路婉婷，许贵桥

(天津师范大学数学科学学院，天津 300387)

1 预备知识

多元连续问题是指定义在多元函数类上算子的逼近问题.这些问题通常用信息基算法求得近似解.本文所用的信息为标准信息，即函数值.信息复杂性n(ε，d)是指对d元函数求得误差小于ε的解而需要的信息算子的最小数.多元连续问题易处理性的概念[1]于1994年引入，其着重研究n(ε，d)当维数d无限变大而ε无限变小时的变化趋势.若n(ε，d)是ε-1或d的指数函数，那么问题被称为不易处理的，否则就称为易处理的.有关易处理性问题的基本知识和结果可参见文献[2-4].本文在平均框架和归一化误差标准下讨论问题，相关定义如下：

(1) 如果存在正数C使得n(ε，d)≤Cdqε-p，则称问题是多项式易处理的；

(2) 如果存在正数C使得n(ε，d)≤Cε-p，则称问题是强多项式易处理的；

(3) 如果存在正数C，t使得n(ε，d)≤Cexp(t(1+lnd)(1+lnε-1))，

(1)

则称问题是拟多项式易处理的；

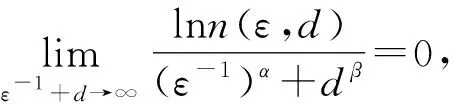
(2)

则称问题是弱易处理的.

在以上概念中，d∈N，ε∈(0，1)，p，q为与d，ε无关的正数.若问题是强多项式易处理的，则满足n(ε，d)≤Cε-p的p的下确界，称为强多项式易处理性的指数，并记作pstr.

2 Korobov空间逼近问题的易处理性

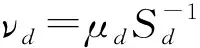
(3)

对任意n，利用Λall的最优算法An，d为

(4)

且其平均误差为

(5)

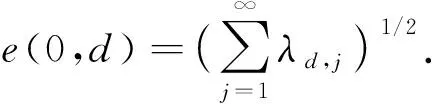
在平均框架下对于归一化误差标准，由文献[2]知利用Λall逼近的复杂性nall(ε，d)(利用nall(ε，d)代替n(ε，d)以区别于标准信息类)为

(6)

基于(6)式，在平均框架下利用Λall逼近的易处理性问题已有大量的研究.[2，4-9]计算函数在一点的值远比计算函数的连续线性泛函容易，因此比较Λstd和Λall的逼近效果成为近期的研究热点.[4，8]但至今未出现Λstd和Λall完全一致的易处理性结果.本文利用文献[10]构造随机逼近算子的思路来证明对文献[5]提出的基于一元Korobov核的多元逼近问题，在易处理问题上Λstd和Λall有相同逼近效果.

以β∈[0，1]，r>1/2为参数的一元Korobov核Rγ，β定义为

假设{gk}满足

1≥g1≥g2≥…>0.

(7)

记Dd=[0，1]d.对d∈N，定义d元Korobov核

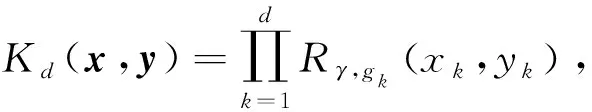
(8)

考虑连续实函数空间C(Dd)上具有零均值高斯测度，且其协方差核为

的Korobov空间在L2(Dd)上的逼近问题：APP={APPd}d∈N.其中对任一固定d逼近问题为APPd：C(Dd)→L2(Dd)，这里APPdf=f，∀f∈C(Dd).

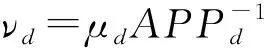
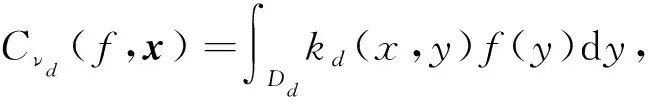
的特征值集合可表示为

Ad={λd，z|Z=[z1，z2，…zd]∈Nd}，

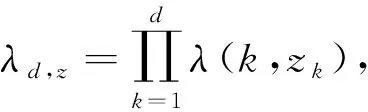
(9)

这里λ(k，1)=1，且

λ(k，2j)=λ(k，2j+1)=gk/j2r，∀j∈N.

(10)

为使用方便，把Ad中的元素重新排列为{λd，i}i∈N，使其满足λd，1≥λd，2≥…≥0.由文献[5]知相应的特征向量为三角多项式，记为ηd，i.由(4)式知其对应的最优算法为

(11)

对于归一化误差标准，文献[5，7-8]得到了问题APP关于Λall具有易处理性的一些结果：

引理1设逼近问题APP={APPd}的gk满足(7)式.对于Λall，有：

(1)APP是多项式易处理的，当且仅当

(12)

(2)APP是多项式易处理的，等价于APP是强多项式易处理的，且

pstr=max(2/(2r-1)，2/(ρg-1))；

(3)APP是拟多项式易处理的，当且仅当

(13)

其中ln+x∶=max(1，lnx)；

(4)APP是一致弱易处理的，当且仅当

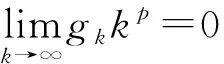
(14)

(15)

定理1设逼近问题APP={APPd}的gk满足(7)式.对于Λstd，有：

(1)APP是多项式易处理的，当且仅当

(16)

(2)APP是多项式易处理的，等价于APP是强多项式易处理的，且

pstr=max(2/(2r-1)，2/(ρg-1))；

(3)APP是拟多项式易处理的，当且仅当

(17)

(4)APP是一致弱易处理的，当且仅当

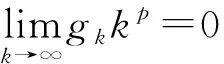
(18)

(19)

证明必要性可由Λstd⊂Λall及引理1给出，下证充分性.对任意固定的整数m

(20)

(21)

(22)

其中

(23)

(24)

(25)

(26)

(27)

(28)

由(24)及(28)式可得

(29)

由(29)式及Fubini定理，

(30)

(31)

由(21)，(30)—(31)式可得

(32)

(33)

下面作迭代.令Ad，0=0，

Ad，kg=Ad，k-1g+Ad，τ(g-Ad，k-1g).

(34)

令Δd，kg=g-Ad，kg，则上式化为

Δd，kg=Δd，k-1g-Ad，τ(Δd，k-1g).

(35)

(36)

由(33)及(36)式可推出

(37)

对任意给定的0<ε<1，在(37)式中令m=nall(ε/2，d)，n=2nall(ε/2，d)且令k=[2log2ε-1]+1，则由(6)式可得到

(38)

由于算法Ad，k仅用到了2([2log2ε-1]+1)nall(ε/2，d)个标准信息且有(38)式成立，因此

n(ε，d)≤2([2log2ε-1]+1)nall(ε/2，d).

(39)

由(39)式和引理1容易检验定理的充分性，由于检验过程所用方法极其常规，这里略去.

注1本文算法是非构造性的，寻找构造性的算法是更有意义的问题.