人体肺呼吸非线性动力学模型的构建及求解

闫 妍，佟 倜，孙媛媛，单桂晔，孙迎春

(1.东北师范大学物理学院国家级物理实验教学中心，吉林 长春 130024；2.吉林大学第二医院胸外科，吉林 长春 130041；3.长春职业技术学院国际交流学院，吉林 长春 130033)

0 引言

氧气是地球上绝大多数生命存活的根本，动植物通过呼吸进行体内外的二氧化碳和氧气的交换，形成了具有一定节奏的物理化学过程及特定的生物节律.生物节律对地球上各种生命的生长发育起到了极其重要的作用.生物节律的紊乱可引起人类发生各类疾病，比如糖尿病、心脑血管疾病、肿瘤等.[1]因此，近年来生物节律成为科研人员高度关注的问题之一，并从实验和理论上进行了深入的研究和探讨.[2-3]果蝇体内具有特定的生物钟机制，并通过实验获得了生物钟的DNA和相关转录蛋白，此项结果对生物节律分子水平上的认识具有开拓性意义，因此，该项成果获得2017年诺贝尔生理医学奖.[4-6]另外，在哺乳类动物体内，由于自身生物钟的调控作用，使得精氨酸和尿素的分泌具有节律性[7].2017年，国际上有78个重要研究团队制定了在基因组范围内研究生物节律的导向[8]，说明对生物节律研究的重要性.

呼吸系统是机体进行内外气体交换的调节器官和通道，也是从外界获取氧气的唯一途径.良好的呼吸状态是维持机体内环境稳定、进行正常生理活动的前提条件.如果肺通气不足，会导致二氧化碳潴留，出现呼吸性酸中毒；若肺通气过度，则会导致二氧化碳排出过多，出现呼吸性碱中毒，致使内环境失稳.[9-10]建立动力学模型进行肺呼吸过程的模拟，对于研究呼吸机理以及预防和治疗肺部疾病具有重要的意义和价值.

正常成年人平静状态下的呼吸是具有一定节律的过程，其周期为4 s左右，参与呼吸各参量之间正负反馈的调节控制具有非线性特征.因此可以采用探讨非线性问题的理论和方法，研究其各参量之间的相互作用及变化行为.研究表明，对人体生理中相对独立的循环系统建立非线性动力学模拟，可以较好地解释其内在参量的作用规律，并与相关实验结果相吻合.本文依据人体肺脏生理结构特点及肺呼吸调节规律，通过分析影响呼吸节律的主要因素及各因素之间的相关性，首次构建一个合理的肺呼吸系统非线性动力学模型，并通过计算机软件平台求出与生理实验结果一致的数值解.

1 模型建立

正常成年人在平静呼吸过程中，肺通气量V(即单位时间内肺泡体积变化率)主要取决于两种因素的作用：(1)机械作用.当肺泡内压p小于体外大气压p0(即Δp=p-p0<0)时，刺激呼吸中枢使呼吸肌收缩，从而引起肺扩张使气体吸入肺内，肺泡体积增大，随后会由于体积增大而产生阻力，进而引起肺扩张反射等负反馈作用来阻碍吸气；当肺内压大于大气压时，呼吸肌自然舒张呼出气体.(2)化学反馈作用.血液(肺泡气)中的CO2浓度升高到一定程度时，刺激脑中枢的相关化学感受器，再经迷走神经传入呼吸中枢，形成正反馈，促进呼吸肌收缩而吸进空气.当血液(肺泡气)中O2的浓度升高时，刺激外周化学感受器，后经迷走神经传入呼吸中枢，形成负反馈，使呼吸肌自然舒张抑制吸进空气.因此，可构建出相对封闭的肺呼吸过程各参量之间相互作用的生理框图(见图1)，以便直观地描述呼吸系统各个参量之间的相互协调作用.

图1 人体肺呼吸过程中各参量之间相互作用的生理框图

在相对封闭的呼吸系统中，肺泡气的二氧化碳分压(pCO2)和氧分压(pO2)的改变是通过二者在血液以及组织细胞新陈代谢过程中的酶促反应实现的，参与呼吸过程的各个量之间存在正负反馈调节作用[11]，其值具有一定的饱和性而不能无限增大.根据以上呼吸机理，依照酶促反应动力学和推广的米氏方程(Michaelis-Menten Equation)[12]，即可构建有理分式形式的非线性微分方程组：

(1a)

(1b)

(1c)

(1d)

该动力学方程可以很好地描述由于机体不断从外界吸收氧气，使血氧含量持续增加，以维持组织细胞新陈代谢活动能够不断进行，并且通过呼气或其他方式排出代谢产物，此循环确保了机体维持稳定及生长代谢正常运行的有效机制.

2 模型求解与分析

2.1 均匀周期振荡解

调节方程组(1)中的24个待定常系数ai为以下数值时，可获得人体肺呼吸过程中各个参量随时间变化的周期振荡解，方程组为：

(2a)

(2b)

(2c)

(2d)

为了直观显示方程组(2a—2d)的数值解变化趋势，做出了该方程组中各参量随时间变化的关系(见图2)，由图2可见，在60 s内，经过很短的暂态后，系统显现出周期振荡模式，共出现14个振荡峰，振荡周期为4 s，这与正常成年人平静呼吸时的实际测试结果完全一致.[13-14]图2中x1，x2，x3，x4变量的波峰、波谷值范围及含义为：

(1) 图2(a)显示的是肺内压与大气压的差值随着呼吸运动在-0.148 7～0.133 5 kPa之间变化；

(2) 图2(b)显示的是肺的功能余气量的最低点值是2.689 L，肺泡单次通气的体积为最高点与最低点数值之差，即3.017与2.689 L之差为0.328 L.若取呼吸频率为 14次/min[13]，则可得到肺泡通气量为V=0.328 L×14 min-1=4.592 L·min-1；

(3) 图2(c)显示的是肺泡气的氧分压值随呼吸运动变化在4.182 9～16.385 6 kPa之间；

(4) 图2(d)显示的是肺泡气中二氧化碳分压值随呼吸运动变化在4.895 7～5.917 2 kPa之间.

4个变量的波峰、波谷值范围的计算结果与临床测定值完全符合(见表1)，说明了模型方程组是合理的.

(a)Δp-t；(b)V-t；(c)pO2-t；(d)pCO2-t

理论与实验值肺内外气压差Δp/kPa肺泡通气量/(L/min)肺泡气氧分压pO2/kPa肺泡气二氧化碳分压pCO2/kPa临床实验值[13-14]-0.26～0.263.5～6.34.0～17.34.7～6.6理论模拟值-0.133～0.1334.5924.2～16.44.9～5.9

为了更进一步直观地显示出方程周期解的特征以及各参量之间的相位关系，做出了各参量之间的相图(见图3).

(a)Δp-V；(b)V-pO2；(c)pO2-pCO2

由图3可见，呼吸系统处于周期振荡状态时，各参量之间的相位关系是经一个暂态后成为一圈闭合的曲线，表示此系统中各参量相互协调作用，达到稳定的往复循环的均匀周期运动状态，表明正常情况下呼吸的均匀性.

以上结果表明，化学反馈和机械反馈是呼吸节律控制和调节最主要的2种负反馈调节因素.

2.2 倍周期解

肺呼吸状态随着人的个体差异、心里活动以及运动状态会有很大的不同，周期一致的呼吸是一种理想状态，通常人体的肺呼吸是非常复杂的不均一状态.因此，为了模拟更接近真实的肺呼吸过程，在均匀周期振荡解的基础上，继续调节动力学模型微分方程组的各个参量前的待定系数，得到一组具有2倍周期的优化参数解，方程组为：

(3a)

(3b)

(3c)

(3d)

方程组(3a—3d)中各参量随时间的变化，经暂态后系统出现明显的2倍周期振荡见图4.其中高位的峰值周期性高低变化，而低位保持不变，说明机体在进入下一个循环前的各参量水平始终保持一致，这也是健康机体呼吸系统内环境稳定的表现.

(a)Δp-t；(b)V-t；(c)pO2-t；(d)pCO2-t

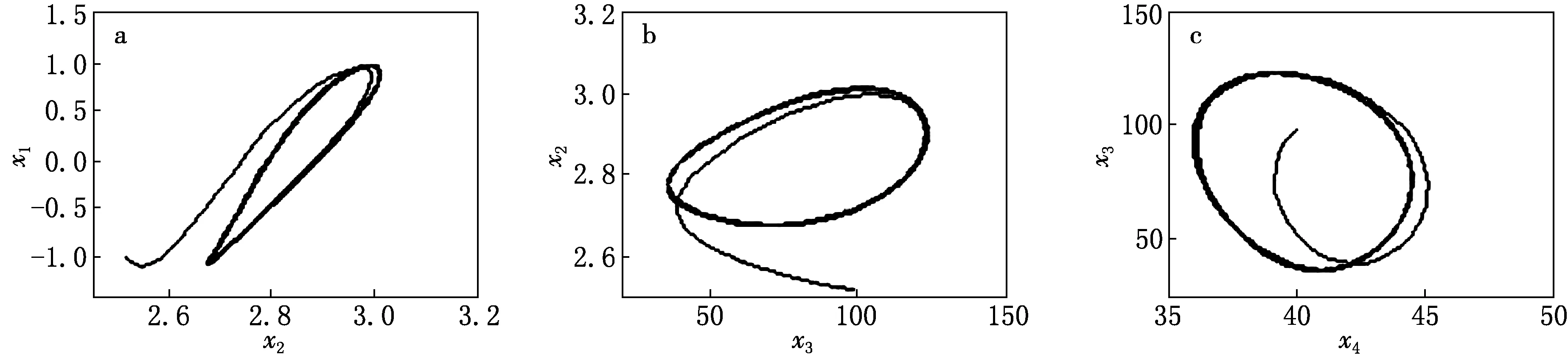
同样可得到具有4倍、8倍周期特征的倍周期解(见图5)，经一段暂态后出现明显的4圈和8圈的封闭曲线，即是分叉现象.这也充分说明了正常情况下，人体肺呼吸并不是遵从严格的均匀周期状态，而是呈现高低起伏的变化状态.

图5 参量pO2-pCO2之间2倍、4倍、8倍周期解相图

2.3 混沌解

实际人体肺呼吸的不均一性不仅会体现出倍周期，还会出现更为复杂的非线性现象.通常临床上认可的肺呼吸监测仪获得的呼吸信息是无确定性规律，但是呼吸频率和单次潮气量必须在一定限度范围内[15]，因此，为了模拟更为复杂的呼吸状态，在均匀周期解和倍周期解的基础上，更为细致地调节各个参量前的常系数，得出一组具有混沌特征的优化参数，方程组为：

(4a)

(4b)

(4c)

(4d)

各参量随时间的动态变化见图6.由图6可见，4个呼吸参量为非周期的不均匀振荡，波峰、波谷大小随时间的变化高低不一，后一状态不能复制前一状态，但幅值都不会超过限制值，且控制在一定范围内，模拟结果体现了肺泡膜张力的弹性和可塑性，呼吸时的自主调控以及对外界因素影响的适应性等.这种现象即为混沌行为，越来越多的研究表明，混沌行为不仅存在于很多的自然现象中，而且在各学科领域还有十分广泛的应用.可利用多项式混沌的方法，对场线耦合的响应不确定度进行量化[16].在地月轨道转移中，应用混沌实现多步控制[17]，可利用量子混沌粒子群优化算法，对分数阶超混沌系统进行参数估计[18].

(a)Δp-t；(b)V-t；(c)pO2-t；(d)pCO2-t

图7显示了各参量相互作用关系的相图.明显可见无限多的闭合曲线出现，且全部闭合曲线都限定在一定范围内，后一时刻与前一时刻的状态完全不重复，说明每一次呼吸的深浅和间隔时间都不是严格一致，有少许的差异，这与实际情况完全相符.因此，该模型证明了肺呼吸运动节律具有混沌特征，也显示了非线性肺呼吸系统从非混沌态到混沌态的演化过程.

(a)Δp-V；(b)V-pO2；(c)pO2-pCO2

3 结果与讨论

首次建立了肺呼吸系统非线性动力学模型，在调节模型方程组的过程中发现，系数a1，a7和λ2对从周期振荡到倍周期现象的调节起关键作用；在倍周期到混沌现象的调节过程中，系数a6的影响很大，当a6的值由原来0.7增大至9.9时，混沌特性就出现了.这表明非线性系统从倍周期分岔到混沌态的演化过程中，控制参数是可在一定范围内变动的，对应的是一个混沌态区域[19].本文从均匀周期振荡、倍周期分岔直到混沌态的演变过程的调节，充分说明呼吸系统具有典型的非线性特征，呼吸节律具有内禀的随机性，其对初始状态具有很强的敏感性[20].此过程也充分体现倍周期分岔现象是非线性系统从非混沌态到混沌态的演化过程的窗口.