一类Block型李超代数的超导子

陈 丹，远继霞，唐孝敏

(黑龙江大学数学科学学院数学系，黑龙江 哈尔滨 150080)

为了简化相对论的费米子与玻色子的统一理论，1974年Wess和Zumino提出了超对称性，将普通时空满足的Poincaré李代数扩充为超Poincaré代数.于是将有限个不同内部量子数的玻色子和费米子放在李超代数的一个不可约表示中，从而拉开了李超代数研究的序幕.[1-2]众所周知，李代数与李超代数有着密切的关系，李超代数的偶部恰为一个李代数.李超代数是在李代数的基础上发展起来的一个代数学分支.[3-4]李超代数分为特征零李超代数和特征p李超代数.关于特征零李超代数的研究，目前已取得了相当丰富的成果.李超代数的研究主要分三个方面：结构、分类和表示.关于李超代数的研究经历了一系列的发展，特别是在单李超代数的结构和表示方面.

李超代数在Killing理论、特征零单李超代数的分类理论[5]、表示理论以及向量场李超代数理论等方面都有着系统的发展.李超代数与李代数的密切联系及其在数学物理领域的重要作用，使李超代数及其相关课题的研究成为数学中较为活跃的领域之一[6-7].在李超代数领域里，特征0的代数闭域中存在着更多的有限维单李超代数和线性无限维单紧李超代数[8].由于李超代数的偶部是一个李代数，所以李超代数的研究方法常借鉴于李代数的研究方法.

近20年来，Block型李代数引起了越来越多学者的关注，并在结构理论和表示理论方面取得了一定的成就.Block型李代数可以通过满足特定条件的代数对(A，D)来构造，而对Block型李超代数的研究尚未实现，因此对满足特定条件的代数来构造Block型李超代数，进而研究其结构具有重要意义.

1 预备知识

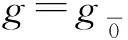
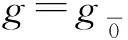
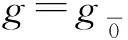
[x，y]=-(-1)|x||y|[y，x]，x，y∈g，

(-1)|z||x|[x，[y，z]]+(-1)|x||y|[y，[z，x]]+(-1)|y||z|[z，[x，y]]=0，x，y，z∈g.

则称g是C上的李超代数.

例1.1设SB(q)是复数域C上的一个代数，其基为{Lα，i，Gβ，j|α，β，i，j∈Z}，运算定义如下：

[Lα，i，Lβ，j]=(β(i+q)-α(j+q))Lα+β，i+j，

[Lα，i，Gβ，j]=(β(i+q)-α(j+q))Gα+β，i+j，

[Gα，i，Gβ，j]=2Lα+β，i+j.

易证，SB(q)为一个李超代数.

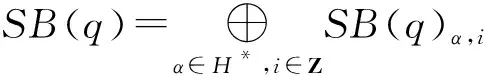
SB(q)α，i=span{Lα，i，Gα，i|i∈Z，α∈H*}.

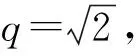
设V和W是复数域上Z-阶化向量空间且齐次分支个数有限，则V和W的Z-阶化诱导为

其中

Homa(V，W)={f∈Hom(V，W)|f(Vb)⊂Wa+b，b∈Z}.

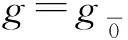
(1) (δx+ηy)v=δ(xv)+η(yv)，δ，η∈C，x，y∈g，v∈V；

(2)x(δv+ηw)v=δ(xv)+η(xw)，δ，η∈C，x∈g，v，w∈V；

(3) 若x∈gλ，v∈Vμ其中λ，μ∈Z2，则xv∈Vλ+μ；

(4) [x，y]v=x(yv)-(-1)|x||y|y(xv)，x，y∈hg(g)，v∈V.

则称V是一个g-模.

设V和W均为g-模，并且非零阶Z-阶化的个数有限，则V和W的模结构诱导了如下Hom(V，W)的g-模结构：x·f(v)=x·(f(v))-(-1)|x||f|f(x，v)，∀x∈g，v∈V.

定义1.3[9]设g是复数域上的一个超代数，V是一个g-模.D∈Hom(g，V)，若满足

D(xy)=(-1)|D||x|x·D(y)-(-1)|D(x)||y|y·D(x)，

则称D为一个g到V的超导子.当V=g时，称D为g的一个超导子.

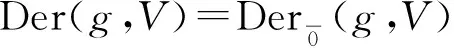
ad(g)⊆Der(g)，[D，ad(g)]=ad(Dg)，

则称ad(g)为g的内超导子集合.集合Der(g)/ad(g)中的元素称为外超导子.

定义1.4[10]商空间

H1(g)=Der(g)/ad(g)

被称为g的系数在伴随模上的一阶上同调群.易证，一阶上同调群是一个超代数，即

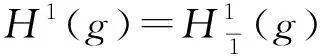
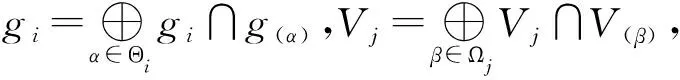
定义1.5[11]设H是作用在复向量空间V上的线性李超代数，φ是定义在H上的取复数值的函数.如果V中存在非零向量ξ，使得Aξ=φ(A)ξ对任意A∈H成立，则函数φ称为H的一个权，ξ称为H的对应于权φ的权向量.下文将零权记为θ.

定义1.6[11]设α∈H*且D∈Der(g)，若满足D(gα)⊆gα，则称D为零权导子.

3 超导子代数及其一阶上同调群

引理3.1[12]设g是一个有限维Z-阶化李超代数，V是一个g-模，则一个具有非零权的权导子φ∈Der(g，V)是内导子.特别地，当g=V时结论同样成立.

证明设φ∈DerD(g，V)，D≠θ.则存在t∈T使得D(t)≠0.因此，对任意的x∈g，都有

d(t)φ(x)=(t·φ)(x)=t·(φ(x))-φ([t，x])=x·(φ(t)).

这说明φ(x)=x·(D(t)-1φ(t))，即φ是一个内导子.

上述引理表明研究超导子时除内导子以外，只需研究零权导子θ即可.

D(Lβ，j)=aβ，jGβ，i+j，D(Gβ，j)=bβ，jLβ，i+j，

(1)

其中β，j∈Z，aβ，j，bβ，j∈C.

引理3.2采取(1)式中的符号.对任意j∈Z，都有D(L0，j)=0.

证明用D分别作用在如下两个等式：

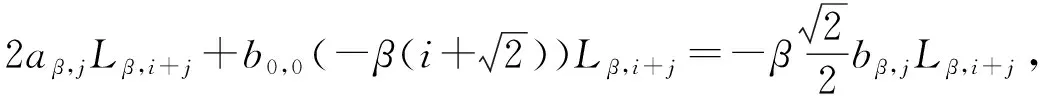
引理3.3采取(1)式中的符号.对任意α，γ，j，k∈Z，都有aα，k=aα，j+k，bγ，k=bγ，j+k.

证明用D作用在等式

上，可得

由于a0，j=0，因此

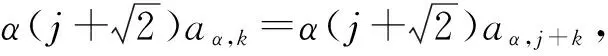
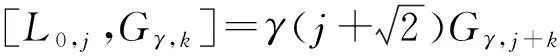
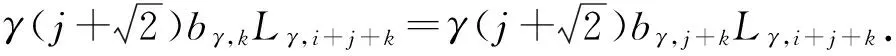
也就是bγ，k=bγ，j+k.

引理3.4采取(1)式中的符号.对任意β，j∈Z，都有

证明用D作用在等式

[Lγ，j，Lfγ，k]=(fγ(j+q)-γ(k+q))L(f+1)γ，j+k

两端，整理系数得faγ，j=afγ，j+k=afγ，j，因此aβ，j=βa1，0.

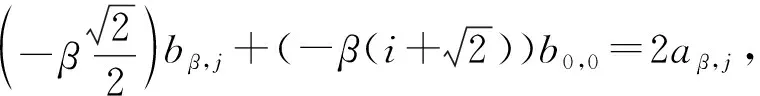
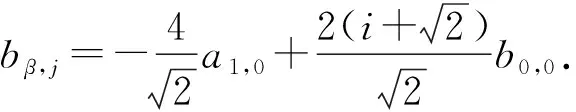
令D1：g→g是一个线性映射，其在g的基底上作用为

D1(Lβ，j)=0，D1(Gβ，j)=Lβ，i+j，β，i，j∈Z.

(2)

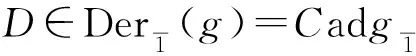
D(Lβ，j)=aβ，jLβ，i+j，D(Gβ，j)=bβ，jGβ，i+j，

(3)

其中aβ，j，bβ，j∈C，β，i，j∈Z.

引理3.5采取(3)式中的符号.对任意β≠0，且β，j∈Z，都有aβ，j=bβ，j.

证明用D分别作用在如下两个等式两端：

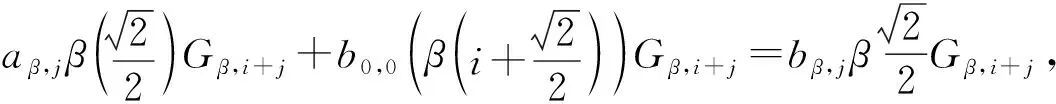
2bβ，jGβ，i+j+2b0，0Gβ，i+j=2aβ，jGβ，i+j.

故有

2bβ，j+2b0，0=2aβ，j.

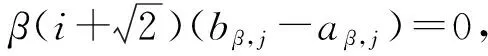
这表明aβ，j=bβ，j.

引理3.6采取(3)式中的符号.则对β≠0及β，γ，j，k∈Z，都有aβ，j=βa1，0+ja0，1.

证明用D分别作用如下两个等式两端：

可得

令d1：g→g是一个线性映射，其在g的基底作用为

d1(Lβ，j)=0，d1(Gβ，j)=Gβ，i+j，β，i，j∈Z.

(4)

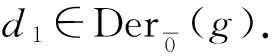
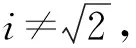
D′(Lβ，j)=0，D′(Gβ，j)=0.

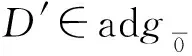
由定理3.1和定理3.2可得如下结论：