小型混流式水泵水轮机损失分析与正交优化设计

严健儒，左志涛，侯虎灿，周 鑫，陈海生



小型混流式水泵水轮机损失分析与正交优化设计

严健儒1,2，左志涛1，侯虎灿1，周 鑫1，陈海生1,2

（1中国科学院工程热物理所，北京 100190；2中国科学院大学，北京 100049）

为了研究各部件对小型混流式水泵水轮机水泵工况和水轮机工况下水力性能的影响，对一小型水泵水轮机进行不同流量下的全流道数值模拟，针对两工况下总压损失集中的叶轮进行正交设计优化。应用L9(34)正交表，选取4个叶轮关键设计参数，以水泵工况扬程偏离率、效率和水轮机工况效率作为目标，进行4因素3水平的正交设计，并通过全流道数值模拟方法和极差分析方法进行选优。结果表明叶片出口直径对泵和水轮机工况性能影响最大，优化后水泵设计工况效率提高了1.06%，水轮机设计工况效率提高1.62%，其相应最优工况点因包角增加而向小流量工况移动。

水泵水轮机；正交优化；水力设计；损失分析

随着化石燃料的短缺及环境污染问题日益严重，积极开发利用太阳能、水能、风能等可再生能源成为能源结构调整的重要途径。为适应这些可再 生能源的大规模开发利用，增加能源系统的综合利用效率，保障电力和能源供应的稳定性，电力储能技术迅速发展[1]。目前的电力储能技术根据能量转换形式，总体上可分为物理储能、电磁储能和化学储能。其中物理储能中的抽水蓄能发展历史长、技术成熟，已在大规模商业系统中运行。

相比于大规模抽水蓄能，小型抽水蓄能机组具有工程位置灵活、投入产出比小、对输电线路要求较低以及能够较好解决个别单位和部门峰荷需要等优点[2]，如海水抽水蓄能和楼宇间抽水蓄能，目前受到国内外学者的广泛关注[3-5]。随着分布式能源的普及，小型抽水蓄能既能作为大规模抽水蓄能的补充，又可以解决分布式能源转化率低、稳定性差的问题。

抽水蓄能机组根据机组类型可以分为四机分置式、三机串联式和二机可逆式，其中二机可逆式结构简单、造价低、土建工程量小，因此得以广泛应用。水泵水轮机是二机可逆式抽水蓄能机组的关键部件，其正向旋转时作为泵使用，消耗电能将水从下水库抽到上水库；反向旋转时作为水轮机使用，来自上水库的水冲击叶轮带动发电机轴旋转发电。作为其核心部件的水泵水轮机的效率和流动状态直接影响抽水蓄能级组的效率和稳定性，所以很有必要对小型水泵水轮机的合理设计进行研究。黄祺等[6]以水轮机工况为主，运用二元设计理论设计了水泵水轮机并进行了内流分析，但是水泵工况效率并不高。王旭鹤等[7]应用全三维反问题设计方法，按照水泵工况给定设计参数设计了水泵水轮机的叶轮，但是水轮机工况叶轮进口冲击损失和叶片背面低压区导致水轮机工况效率降低，需要进一步优化叶片设计。毛秀丽等[8]采用二元理论结合螺旋势流设计了低水头下的混流式水泵水轮机，并且比较了三种导叶形式和厚度对两种设计工况下效率的影响，发现对称式的导叶更适合两种工况。可以看出，在对水泵水轮机初步设计之后，有必要进行优化设计来提高两种工况的水力效率。

正交试验设计是研究多因素多水平的一种设计方法，它是根据正交性从所有试验中挑选出部分有代表性的点进行试验。这些有代表性的点具备了“均匀分散，齐整可比”的特点，使用正交设计方法可以高效快速地进行优化，减少试验次数。目前正交设计方法已经广泛应用于泵的设计优化，但是对于水泵水轮机的应用很少。高雄发等[9]选取旋流泵的叶轮外径、叶片数、叶片宽度、叶片出口安放角、叶片进口安放角为主要因素，对原型泵的扬程和效率进行了优化。优化后泵效率提高4.2%。郭晓梅 等[10]对诱导轮离心泵的前置孔板进行了正交数值模拟，得到了有效抑制诱导轮离心泵小流量下不稳定特性的最佳参数组合的孔板。侯虎灿等[11]对一种IS系列泵的前置导叶进行了正交设计优化，综合考虑了扬程和水力效率随主次因素的变化，优化后加装前置导叶的泵效率提高1.43%，总能耗节约2.06%。综上，正交设计可以有效地对目标水平进行优化。

本文运用二元设计理论完成了小型水泵水轮机的水力初步设计，并结合数值模拟结果分析各关键部件损失。针对损失影响最大部件叶轮进行正交优化设计，采用4因素3水平的正交表，以叶片出口直径、出口宽度、叶片出口安放角和叶片包角为因素设计9组叶轮，并探究这些变量对水泵工况效率、扬程和水轮机工况的效率影响。基于此，获得各关键参数的影响规律及最终优化方案，为小型水泵水轮机的性能优化提供参考。

1 小型混流式水泵水轮机水力设计

混流式水泵水轮机水流沿径向进入叶轮，然后沿轴向流出。理论上相同水头和转速下，水泵的叶轮直径为水轮机1.4倍，实践也证明水泵作为水轮机反转时效果较好，水轮机反转抽水性能较差。所以水泵水轮机设计时一般以泵为基础，以水轮机工况的性能作为校核[12]。整个水力设计方法流程如图1所示。

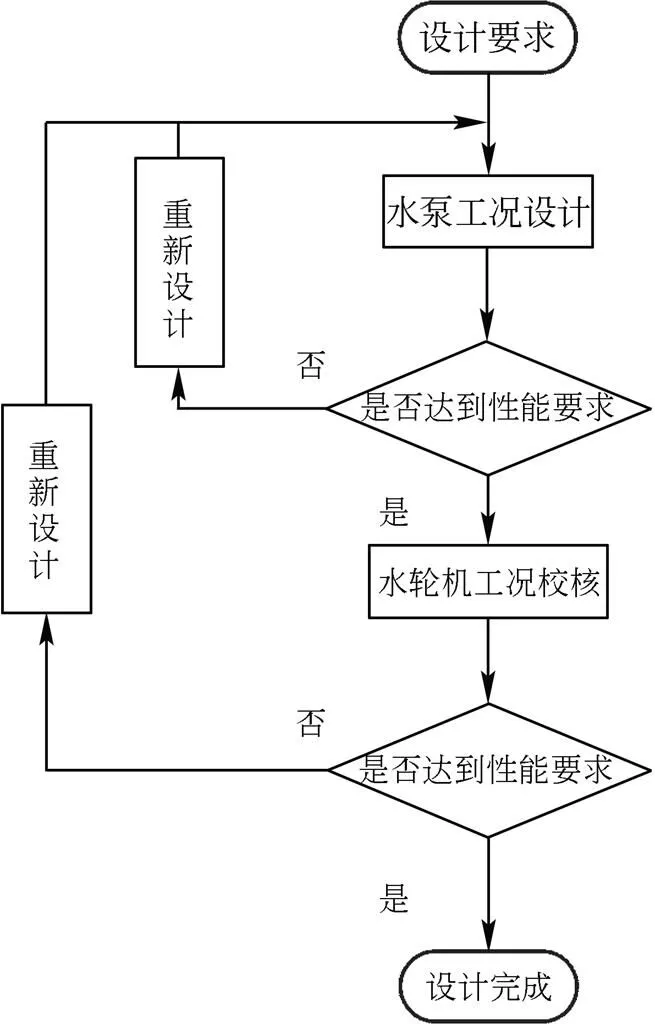
图1 小型水泵水轮机设计流程图

小型混流式水泵水轮机形状类似于离心泵，叶片包角大，流道狭长，叶片数一般为6或7[12-13]，高水头转轮可达9片。在这一范围内叶片数对水泵工况和水轮机工况的水力性能没有明显影响[6]。叶轮为了适应水轮机工况，出口安放角一般为16°～20°。对于蜗壳的设计，水泵工况下为了防止脱流，蜗壳面积的扩散度不能过大，水轮机工况下则希望较大的断面来使水流均匀进入叶轮。实践证明大断面的蜗壳更能较好地同时适应两种工况[14]。

根据小型抽水蓄能的应用范围[2]，基本参数设置为设计水头18 m，设计流量为50 m3/h。通过初步设计得到的小型水泵水轮机如图2所示，包括尾水管、叶轮、蜗壳和出口段。其中叶轮为闭式叶轮，叶片数为6片，叶轮直径为141.5 mm，叶片出口安放角为 20°，叶片包角为140°。蜗壳基圆直径为156 mm，进口宽度为20.5 mm，隔舌安放角为18°，扩散段长度为120 mm，扩散角为10°。设计所得水泵水轮机如图2所示。

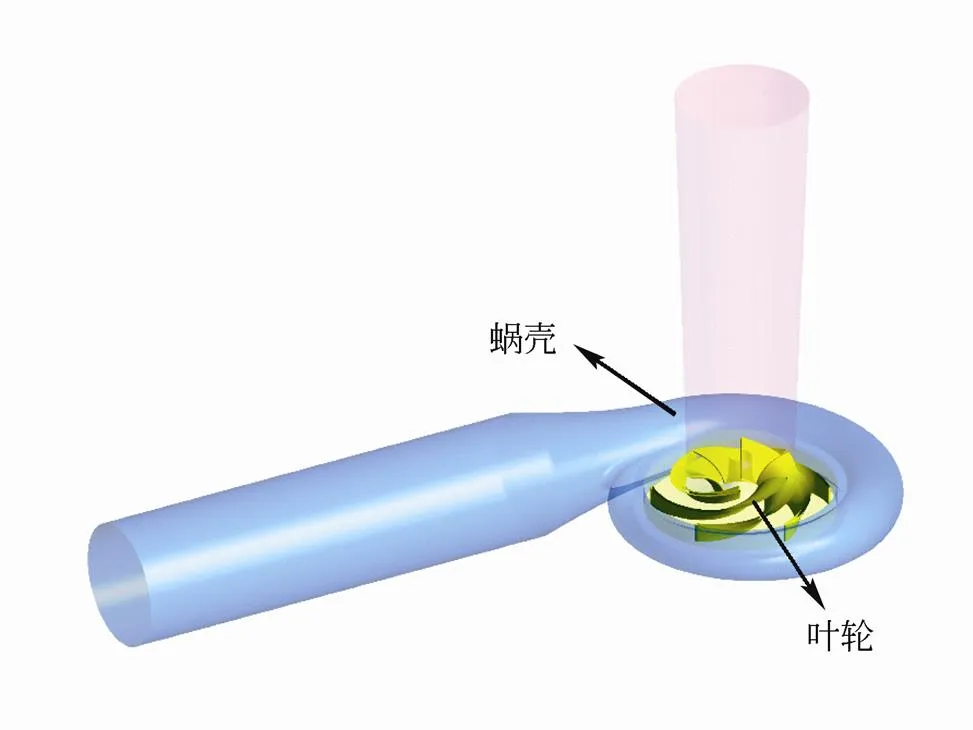
图2 小型水泵水轮机结构模型

2 水泵水轮机数值模拟

数值模拟使用TurboGrid和ICEM进行各个部件的结构化网格划分，最后在Ansys CFX里进行全流道的数值计算，整个水泵水轮机的计算域如图3所示。为了减少出口边界对内部流动影响，保证流动稳定性，对进口管和出口段进行了延伸。流动控制方程的离散采用耦合了有限元的有限体积法，湍流模型选用模型，壁面函数选用Scalable壁面函数。整个计算区域中，叶轮为转动部件，其余部件均为静止部件，动静交界面采用Frozen rotor。为了更准确地反映壁面附近的流动状况，对曲率变化较大的部位，如叶片前缘、叶片后缘以及蜗壳隔舌处进行边界层加密处理，计算所得整体壁面的+最大值为179.4，满足计算要求。固壁处采用无滑移边界条件。

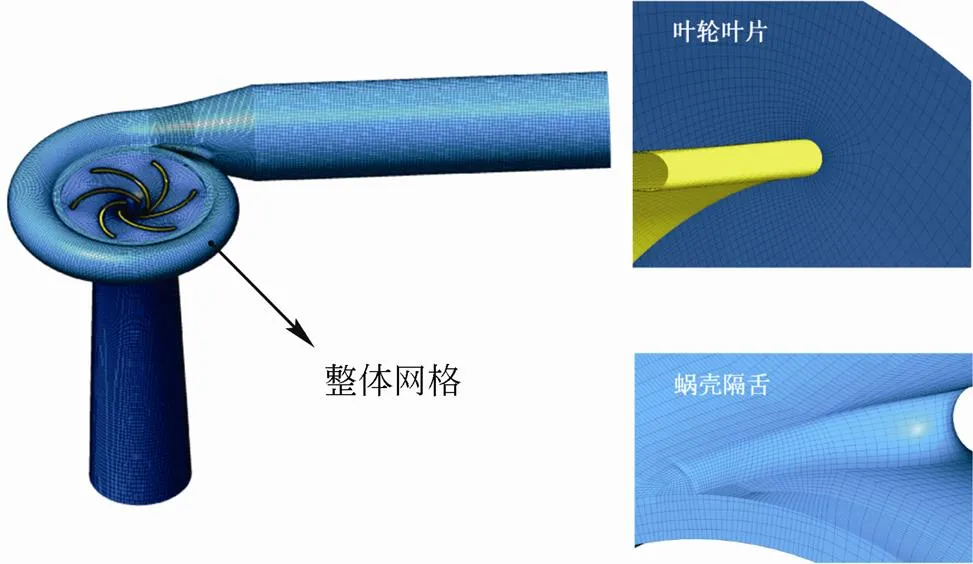
图3 小型水泵水轮机计算域及网格

水泵工况下，进口给定总压边界条件，相对总压设定为0 Pa。出口给定流量边界条件，水轮机工况下，进口给定流量边界条件，出口给定1个大气压的平均静压边界条件。

为了尽量降低网格数量对计算结果的影响，同时兼顾准确性和计算时间，本文对计算网格进行了网格无关性分析。以原型水泵水轮机为例，将额定工况点的扬程和水力效率η设为指标，计算结果如表1所示。

由表1可知，当网格数大于462万之后，模型泵的扬程和效率都趋于稳定，扬程值相差在0.0075%，效率相差在0.011%以内。综合考虑后选取462万左右网格作为后续模拟计算的网格数。

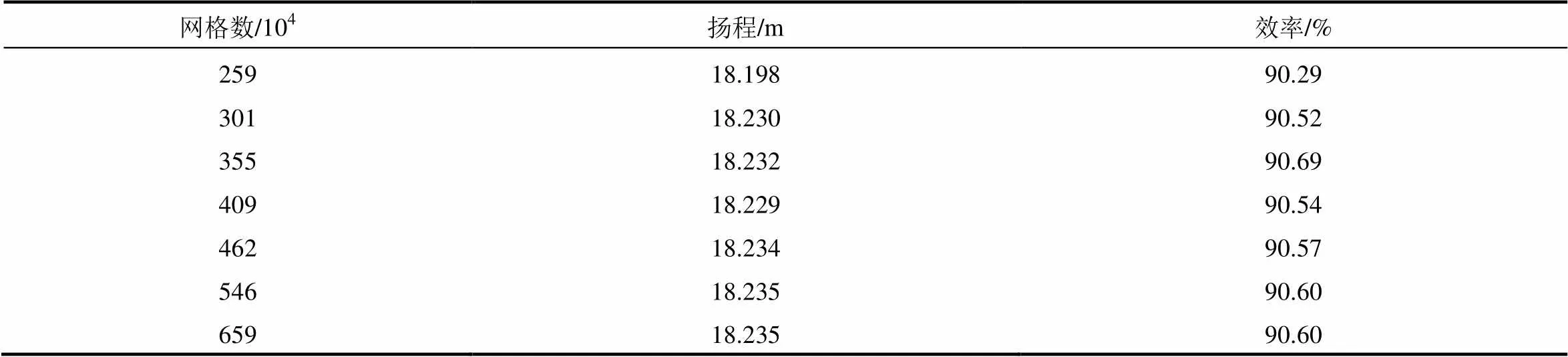
表1 网格无关性评估

确定网格量之后，本文选取已公开实验结果的混流式水轮机HLA696-LJ-108进行计算模型可靠性验证，水轮机计算域如图4所示。网格量选取470万，蜗壳进口给定总压条件，尾水管出口给定流量边界条件。计算结果对比了3个工况点，发现计算结果与试验结果的最高效率差为1.6%，如表2所示，表明采用该计算模型预估水泵水轮机转轮在不同运行工况下的效率是可行的。

表2 数值验证

图4 数值验证全流道计算模型

3 关键部件损失分析

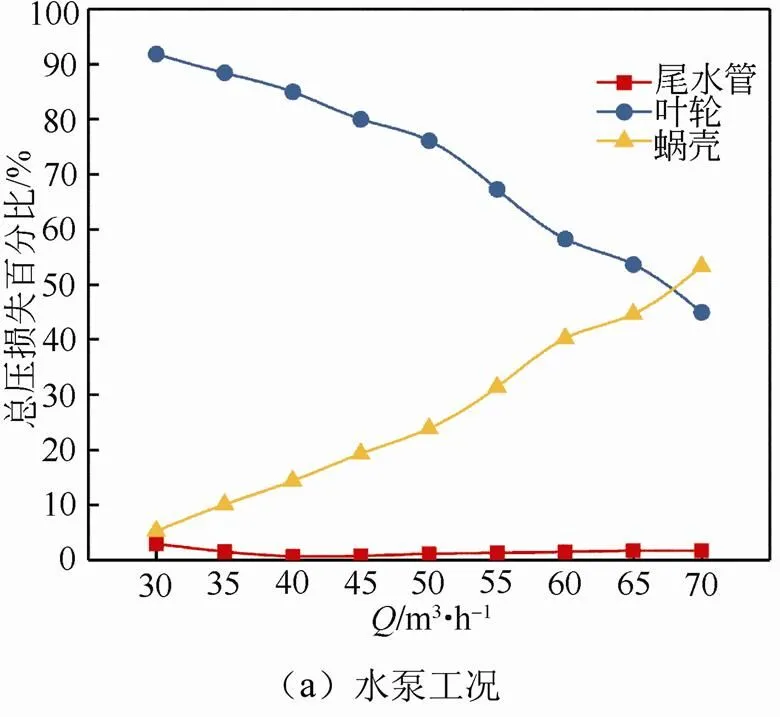
对30～70 m3/h流量范围内的水泵与水轮机两种工作状态下流场进行模拟，各部件总压损失计算方法如下：尾水管和蜗壳的总压损失为各自进出口总压之差，而叶轮的总压损失为水泵水轮机整体进出口的总压损失减去尾水管和蜗壳的总压损失。计算后各部件的总压损失百分比如图5所示。由图5(a)中不同流量下各部件的水力损失百分比可以看出，水泵工况下，除最大流量外的绝大多数工况下叶轮的水力损失在总损失中占比较大，均高于总损失的50%。当流量进一步增大到1.4倍设计流量，即更加偏离设计工况时，由于蜗壳中流动分离严重，蜗壳内部的水力损失开始占主导地位。由图5(b)可知，水轮机工况下，由于蜗壳在叶轮之前，所以一直流动状况良好，水力损失小。流量不断增大时，尾水管中流动损失增加，但水力损失大部分始终集中在叶轮处，损失占比均高于70%。综上可知， 对叶轮进行优化设计是提高水泵水轮机水力效率的关键。

4 正交优化设计

正交设计试验可以找出各优化变量对指标的影响程度，叶轮的主要设计参数有叶轮出口直径、叶轮进口直径、叶片出口直径、出口宽度、出口安放角、进口安放角、叶片扭角和叶片包角。合理地选择叶轮设计参数可以保证较小尺寸下达到扬程要求并提高两种工况的效率。叶片出口直径和出口宽度将直接影响叶轮的做功能力和通流量，进而影响两工况的效率。出口安放角会影响泵工况扬程和水轮机工况的进口冲击[15]，属于典型的在水泵水轮机设计中应兼顾的变量。包角大小直接影响流道长度，过大时摩擦损失显著，效率下降；过小时流道中易出现二次流现象[16]，且叶片做功能力下降明显。因此，本文中将针对叶片出口直径2、出口宽度2、出口安放角2a和叶片包角这四个因素进行研究，每个因素分别根据文献和经验，取3个水平如表3所示，选用L9(34)正交表确定的正交设计方案如表4所示。原型水泵水轮机的因素组合即为2222。

表3 正交因素水平表

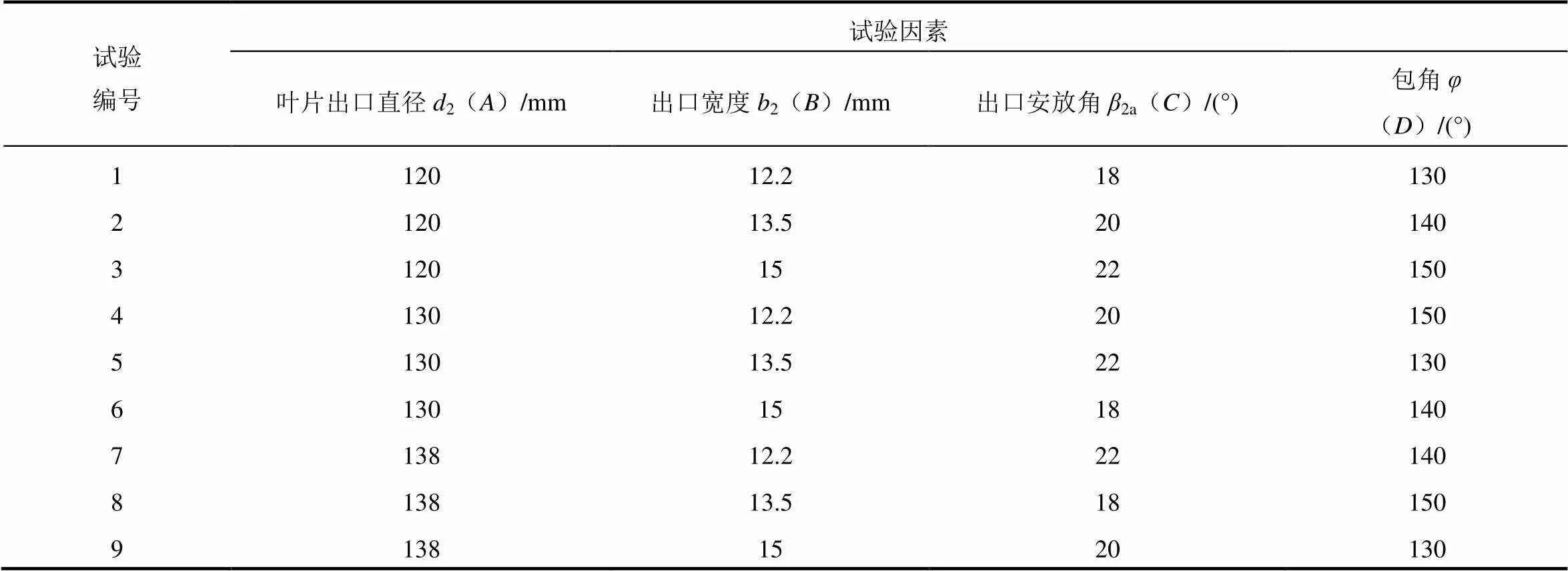
表4 正交试验方案

水泵水轮机需要在两种工况下运行以满足抽水和发电的要求，所以优化时需要兼顾两种情况的效率，因此本文将正交设计优化的指标确定为水泵设计工况的效率p和水轮机设计工况的效率t，以及为了保证设计扬程（水泵设计扬程d=18 m）而引入的扬程偏移百分比。本文将研究4个变量对这三个指标的影响权重，在尽量减少设计水头偏离的情况下，提高两种设计工况的效率。扬程偏移百分比如式(1)计算。

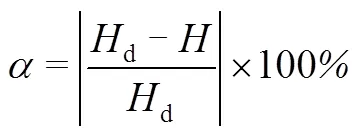
5 正交设计结果分析

根据正交试验方案设计分析得到9组水泵工况和水轮机工况的水力效率，如表5所示。

从表5可以看出，水泵效率最高的是6号方案，p=91.59%。水轮机效率最高的是2号方案，t=90.91%。编号1、2、3偏离设计扬程18 m最严重。为分析各个设计参数对水泵水轮机的性能影响权重，并找到影响效率的主要因素和优化方案，需要对模拟结果进行极差分析，结果如表6所示。其中K表示相应水平的几种模拟情况的指标之和，而M为相应水平的指标平均值，是各平均值的极差。为了更直观地反映试验因素的水平改变对试验结果的影响，以因素的变化水平为横坐标，以各指标平均值为纵坐标，所做的折线图如图6所示。

表5 数值模拟结果

图6 3个指标与各因素关系

由图6的极差分析可以看出，叶轮这4个变量对两种设计工况下水力性能的影响是各不相同的，极差越大说明该列因素的水平变化对试验指标在数值上的变化影响越大。因此，通过比较极差的大小，可以获得叶片出口直径、出口宽度、出口安放角和叶片包角对泵工况下水力效率、扬程和水轮机工况下水力效率的影响程度。各设计参数对水泵工况效率p的影响主次顺序为，对水泵工况扬程偏移量百分比的影响主次顺序为，对水轮机工况效率t的影响主次顺序为，可见在水泵水轮机叶轮参数设计中，应该优先考虑叶片出口直径对泵工况下水力效率、扬程和水轮机工况下水力效率的影响。就正交设计中的单个因素而言，比较该因素下各个水平试验指标数值的大小，可以得出该因素各个水平对该试验指标影响的主次顺序。因素对p的影响顺序为213，对的影响顺序为132，对t的影响顺序为123。因素对p的影响顺序为231，对的影响顺序为132，对t的影响顺序为213。因素对p的影响顺序为132，对的影响顺序为213，对t的影响顺序为132。因素对p的影响顺序为321，对的影响顺序为132，对t的影响顺序为231。综合考虑以上三个指标，选定2213为兼顾设计水头和两种工况效率的最优组合。

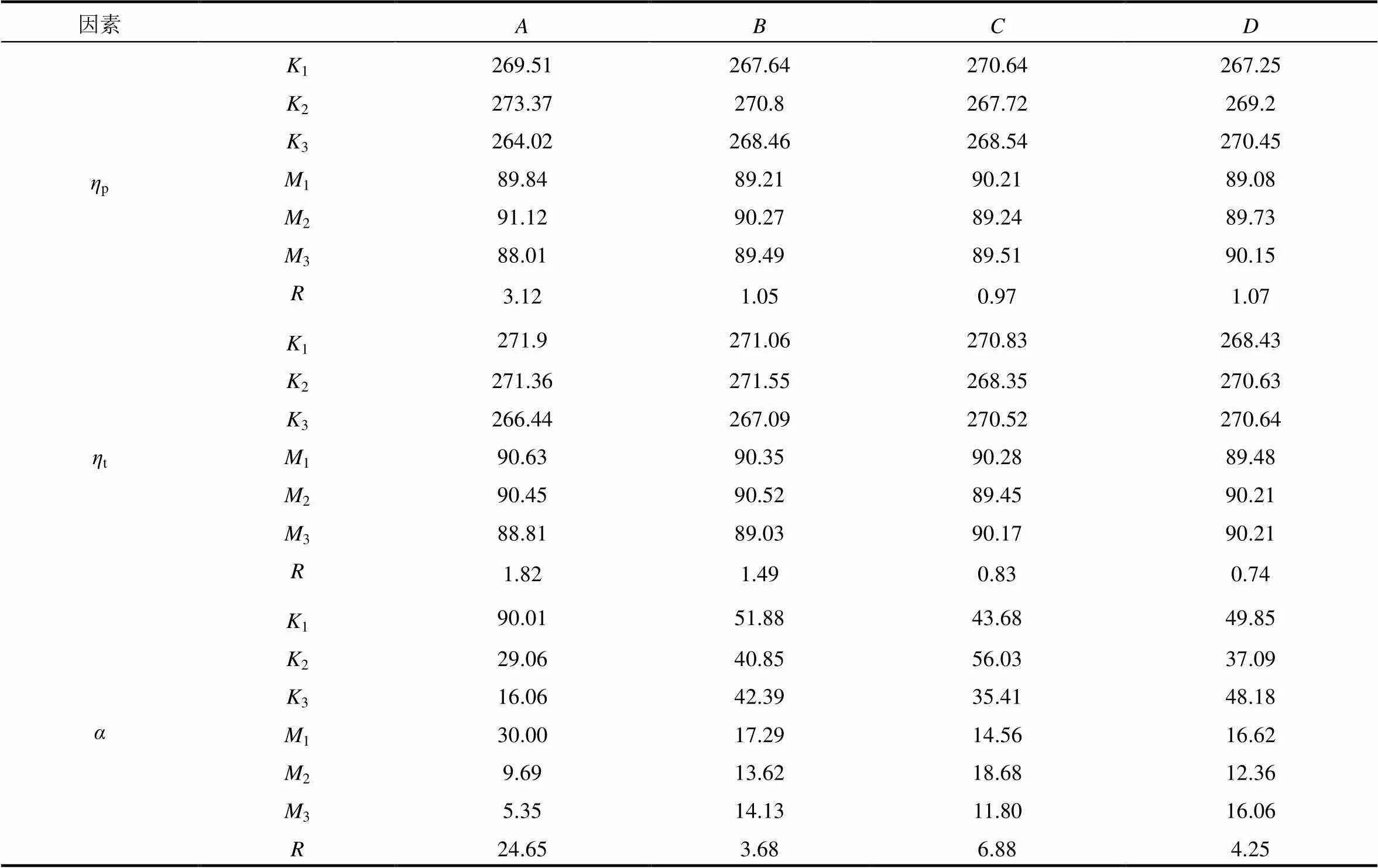
表6 数值模拟结果极差分析

最优组合中叶片出口直径2=130 mm，出口宽度2=13.5 mm，出口安放角2a=18°，叶片包角=150°，和原型2222相比，优化后的水泵水轮机叶轮出口安放角减少2°，包角增大10°，如图7所示。利用Ansys CFX对最佳方案进行全流道的数值模拟计算，将优化后的水泵和水轮机两种工况下不同流量的性能曲线分别与优化前对比，如图8所示。

图7 优化前后出口安装角对比

图8中可以看出，优化后水泵水轮机的流量效率曲线在设计点和小流量工况下都比原型水泵水轮机要高。水泵设计工况点优化后效率为91.66%，扬程为17.69 m，比原型水泵水轮机泵效率高出了1.06%，扬程略有下降。在(0.5～1.0)d范围内，整体效率都有提高且平均提高1.23%。与正交结果中的9种方案对比泵工况效率比较理想，验证了正交设计方法的可行性。水轮机工况流量效率曲线的变化和水泵性能曲线变化类似，小流量和设计工况点的水轮机工况效率都有提高，整体效率曲线向小流量方向偏移。在设计流量50 m3/h处，优化后水轮机工况效率提高1.62%。在(0.5～1.3)d范围内，整体效率平均提高2.67%。，和优化前的原型机相比，水泵工况扬程下降是因为出口安放角的略微调整（减小2°）。而水泵工况和水轮机工况的流量扬程曲线向小流量下移动，主要是因为包角增加，流道相对变长，大流量下摩擦损失显著增加，导致效率下降，最佳效率点向小流量方向移动。

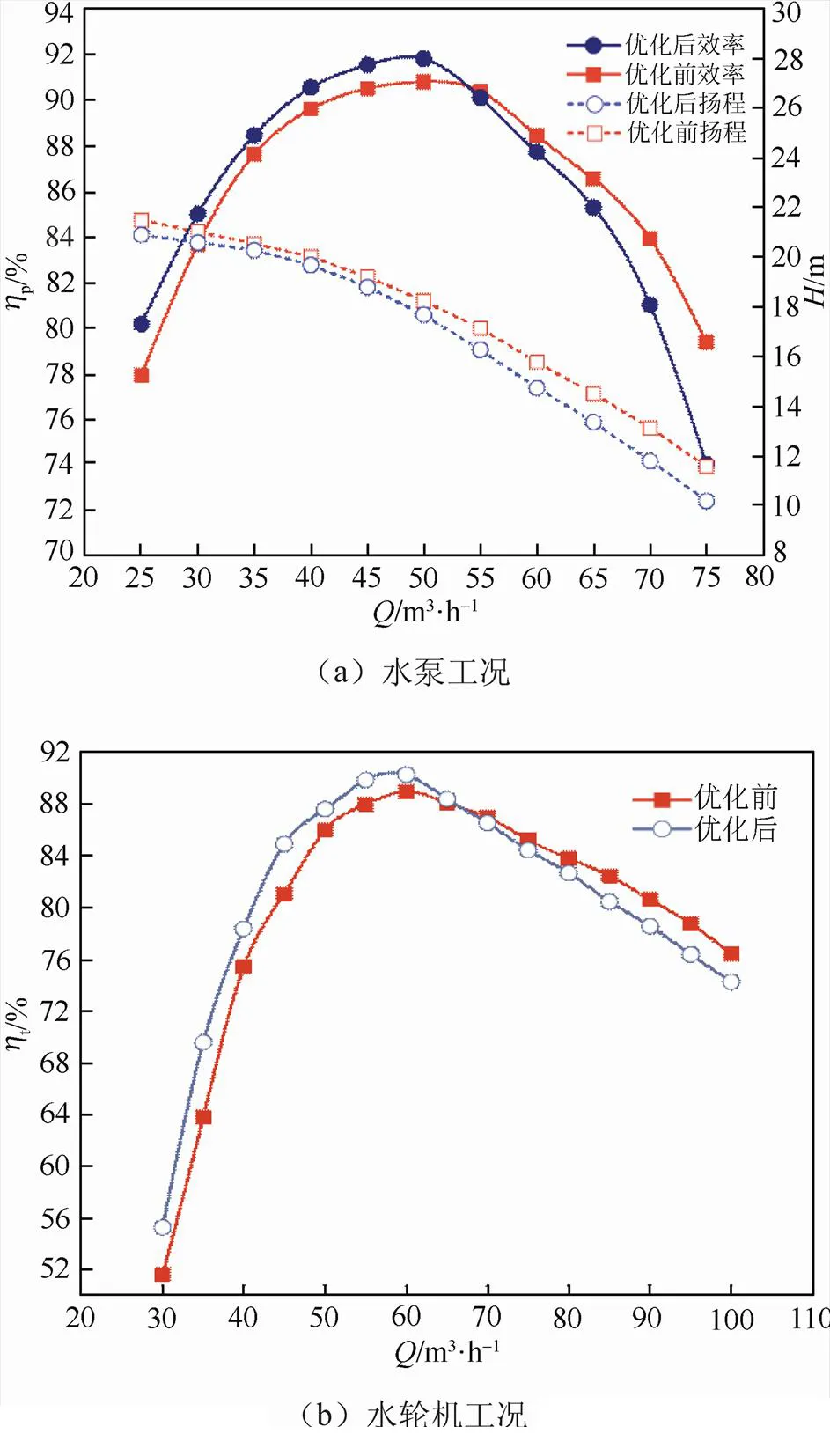
图8 优化前后性能曲线

6 结 论

本文对水泵水轮机不同流量下水泵工况和水轮机工况进行全流道数值模拟，在分析了主要部件的总压损失后，针对叶轮进行了正交设计优化，得到如下结论。

（1）优化前水泵工况下，流量在(0.6～1.3)d时，叶轮处总压损失超过50%。流量为1.4d时，蜗壳中的损失大于50%；水轮机工况流量在(0.6～1.4)d时，叶轮处总压损失均超过70%。

（2）各设计参数中叶轮出口直径对水泵工况的扬程、效率和水轮机工况效率影响最大，出口宽度、出口安放角和叶片包角次之，且其相互间主次关系受评价参数影响。

（3）对于正交优化设计后的水泵水轮机，水泵设计工况点效率提高1.06%，水轮机设计工况点效率提高1.62%，两工况性能曲线因包角增加向小流量工况偏移。

[1] 严晓辉, 徐玉杰, 纪律, 等. 我国大规模储能技术发展预测及分析[J]. 中国电力, 2013, 46(8): 22-29.

YAN Xiaohui, XU Yujie, JI Lv, et al. Forecasting and analysis on large-scale energy storage technologies in China[J]. Electric Power, 2013, 46(8): 22-29.

[2] 周学志, 徐玉杰, 谭雅倩, 等. 小型抽水蓄能技术发展现状及应用前景[J]. 中外能源, 2017, 22(8): 87-93.

ZHOU Xuezhi, XU Yujie, TAN Yaqian, et al. Development status and application prospects of small-scale pumped hydro energy storage technology[J]. Sino-Global Energy, 2017, 22(8): 87-93.

[3] SINGH P M, CHEN Z, CHOI Y D. Hydraulic design and performance analysis on a small pump-turbine system for ocean renewable energy storage system[J]. Journal of Mechanical Science & Technology, 2017, 31(11): 5089-5097.

[4] TAGARE D. Hydroelectric generation pumped storage, minor hydroelectric, and oceanic based systems[M]. USA: John Wiley & Sons, Inc. 2011: 45-68.

[5] 陈海生, 谭春青, 孟爱红, 等. 微型抽水储能系统: 102477931A[P]. 2012-05-30.

CHEN Haisheng, TAN Chunqing, MENG Aihong, et al. Minitype water pumping energy storage system: 102477931A[P]. 2012-05-30.

[6] 黄祺. 可逆式水泵水轮机水力设计及内部流场分析[D]. 兰州: 兰州理工大学, 2012.

HUANG Qi. Hydraulic design and internal flow field analysis of pump-turbine[D]. Lanzhou: Lanzhou University of Technology, 2012.

[7] 王旭鹤, 祝宝山, 樊红刚, 等. 水泵水轮机转轮三维反问题设计与特性研究[J]. 农业机械学报, 2014, 45(12): 93-98+116.

WANG Xuhe, ZHU Baoshan, FAN Honggang, et al. 3D inverse design and performance investigation of pump-turbine runner[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(12): 93-98+116.

[8] 毛秀丽, 郑源, 屈波, 等. 小型混流式水泵水轮机水力设计[J]. 南水北调与水利科技, 2014, 12(6): 123-126+158.

MAO Xiuli, ZHENG Yuan, QU Bo, et al. Hydraulic design of small mixed-flow reversible pump turbine[J]. South-to-North Water Transfers and Water Science & Technology, 2014, 12(6): 123- 126+158.

[9] 高雄发, 施卫东, 张德胜, 等. 基于CFD正交试验的旋流泵优化设计与试验[J]. 农业机械学报, 2014, 45(5): 101-106.

GAO Xiongfa, SHI Weidong, ZHANG Desheng, et al. Optimization design and test of vortex pump based on CFD orthogonal test[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(5): 101-106.

[10] 郭晓梅, 朱祖超, 崔宝玲, 等. 基于正交试验的诱导轮前置孔板的参数化研究[J]. 工程热物理学报, 2011, 32(8): 1319-1322.

GUO Xiaomei, ZHU Zuchao, CUI Baoling, et al. Study of pre-positioned orifice's parameters before the inducer based on orthogonal test[J]. Journal of Engineering Thermophysics, 2011, 32(8): 1319-1322.

[11] 侯虎灿, 张永学, 李振林, 等. 离心泵前置导叶的正交优化设计[J]. 工程热物理学报, 2015, 36(12): 2618-2623.

HOU HuCan, ZHANG Yongxue, LI Zhenglin, et al. Optimization design of inlet guide vane in a centrifugal pump based on orthogonal method[J]. Journal of Engineering Thermophysics, 2015, 36(12): 2618-2623.

[12] 梅祖彦. 可逆式水泵水轮机的若干设计问题[J]. 华北电力技术, 1988(4): 45-49+59.

MEI Zuyan. Some design problems of reversible pump turbine[J]. North China Electric Power, 1988(4): 45-49+59.

[13] 盛树仁, 房壮为. 可逆式水轮机转轮水力设计的探讨[J]. 大电机技术, 1983(5): 45-52+2.

SHENG Shuren, FANG Zhuangwei. Discussion on hydraulic design of reversible turbine impeller[J]. Large Electric Machine and Hydraulic Turbine, 1983(5): 45-52+2.

[14] 张兰金. 大型混流式水泵水轮机转轮的研究[D]. 北京: 中国农业大学, 2007.

ZHANG Lanjin. Research on large mixed flow pump turbine runner[D]. Beijing: China Agricultural University, 2007.

[15] 阮辉, 廖伟丽, 赵亚萍, 等. 叶片高压边安放角对高水头水泵水轮机性能的影响[J]. 排灌机械工程学报, 2015, 33(3): 220-225.

RUAN Hui, LIAO Weili, ZHAO Yaping, et al. Effects of blade angle at high pressure end on performance of pump- turbine with high head[J]. Journal of Drainage and Irrigation Machinery Engineering, 2015, 33(3): 220-225.

[16] 马达. 可逆式水泵水轮机叶片包角对性能影响的研究[D]. 兰州: 兰州理工大学, 2013.

MA Da. The research on the influence of blade angle to the performance of pump-turbine[D]. Lanzhou: Lanzhou University of Technology, 2012.

Loss analysis and design optimization of a small scale mixed-flow pump turbine using the orthogonal method

YAN Jianru1,2, ZUO Zhitao1, HOU Hucan1, ZHOU Xin1, CHEN Haisheng1,2

(1Institute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing 100190, China;2University of Chinese Academy of Sciences, Beijing 100049, China)

Numerical simulations were performed on a small scale pump turbine device under different flow conditions. The impeller on which the total pressure loss concentrates was optimized using the orthogonal method. A L9(34) orthogonal table was produced with four important design factors for an impeller at three levels. The optimization considered pump head deviation, pump efficiency and turbine efficiency. The results showed that the blade outlet diameter affected significantly the performance of pump turbine. Compared with the original baseline pump turbine, the optimized pump efficiency increased by 1.06% and the optimized turbine efficiency increased by 1.62% under the design conditions. Both the optimized efficiency points under the pump and turbine operating conditions moved toward to a low flow rate due to the augment of the wrap angle.

pump turbine; orthogonal optimization; hydraulic design; loss analysis

10.12028/j.issn.2095-4239.2018.0093

TK 734

A

2095-4239（2018）05-913-08

2018-06-16；

2018-07-05。

国家重点研发计划（2017YFB0903604），国家自然科学基金（51606188），中国科学院洁净能源先导科技专项（XDA20170200）及中国科学院前沿科学重点研究项目（QYZDB-SSW-JSC023）。

严健儒（1994—），男，硕士研究生，主要研究方向为水泵水轮机设计，E-mail：yanjianru@iet.cn；

陈海生，研究员，主要研究方向为新型大规模电力储能系统与材料、微型燃气轮机、微小尺度流动与传热等，E-mail：chen_hs@mail.etp.ac.cn。