丛聚的含气泡水对线性声传播的影响∗

范雨喆 陈宝伟 李海森 徐超

1)(哈尔滨工程大学,水声技术重点实验室,哈尔滨 150001)2)(海洋信息获取与安全工信部重点实验室(哈尔滨工程大学),工业和信息化部,哈尔滨 150001)3)(哈尔滨工程大学水声工程学院,哈尔滨 150001)(2018年4月18日收到;2018年5月18日收到修改稿)

1 引 言

含气泡水是重要的自然及工业现象,常见于舰船螺旋桨空化、水下爆炸和生物医学应用等领域中[1−3].关于含气泡水中的线性声传播问题已有大量研究,主要基于两种方法.其一是通过集平均[4]或体积平均[5]建立起描述含气泡水内的声传播的基本方程,在结合气泡动力学方程[6]后,对整体做线性化近似.当然,这些线性声传播理论由于忽略了气泡间的相互作用,会在含气泡水浓度较高时产生较大误差.通过考虑气泡与含气泡水中的平均量相互作用,可以初步解决这一问题[7−10].另一种方法则是先对气泡动力学方程做线性化近似,在此基础上将含气泡水中的声传播问题看作多体多次散射问题[11,12].同样,在含气泡水气泡体积分数较高时,需引入气泡间的再辐射对理论进行修正[13−16],这种方法也被称为多泡散射法(multiple-scattering approach,MST)[17].在不考虑气泡间相互作用时,上述两种方法在线性声传播框架内的结论是一致的.此外,也可以寻求该问题的数值求解办法,但是其过高的计算量阻碍了精确仿真环境的建立[18].

然而,这些研究的一个共同的重要假设是:气泡在空间均匀分布且相互间统计独立.这导致含气泡水中声传播理论大多忽略了含气泡水内气泡的空间分布对声传播的影响.事实上,含气泡水中气泡在空间上分布并均匀是十分严苛的条件,即使在实验室环境中也很难达到.现有的含气泡水线性声传播实验中,相速度和衰减系数的峰值往往低于理论预测值,且存在低频偏移[19,20].通过实验观测[21],多分散的含气泡介质内气泡间可能存在小范围的聚集趋势(在后文统一称作丛聚现象),这为合理解释预测和测量结论间的偏差提供了研究方向.本文基于MST框架,将准晶体近似(quasi-crystalline assumption,QCA)引入自洽方法(self-consistent approach,SCA)[21,22],推导出了考虑空间分布时多分散介质中的等效声波波数形式,并在此基础上引入Neyman-Scott点过程(Neyman-Scott point process,NSP)描述了含气泡水内气泡小范围的丛聚现象[23],给出了丛聚气泡水内等效声波波数.考虑到空间分布的统计信息提取对相关研究的精确与否起到重要作用,本文引入了一种比例无偏估计,通过该方法获得了仿真环境下丛聚含气泡水模型的相速度及衰减系数,该建模及统计方法也可作为相关实验工作的理论基础.

2 气泡水中声传播的自洽方法

2.1 气泡的小幅度振动

考虑气泡在声场作用下的动力学方程,假设其在振动过程中始终保持球形,并忽略气泡与水间的质量交换,气泡的径向振动可由Prosperetti修正的Keller-Miksis方程[6]表示为

其中pin为

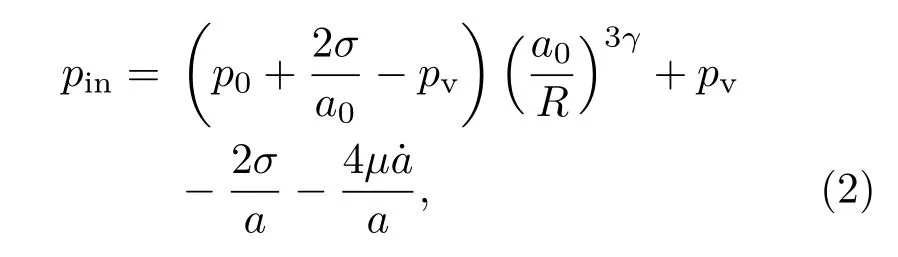
其中p0为环境大气压,pv是泡内蒸汽压,σ是液体表面张力,µ是液体的黏滞系数,c0为声波在液体中的传播速度,ρl是液体密度,γ是泡内气体的多方指数,a0是气泡初始半径,a=a(t)为气泡任意时刻的半径,p∞为声场和环境压力.(1)式在低Mach数下,能准确地模拟气泡在声场中振动的动力学过程.对(1)式做一阶微扰处理,此时稳态的气泡随声场做同频率周期振动,假设a(t)=a0(1+X),p∞=p0(1−εe−jωt)和pin=pin,equ(1−ΦX),可得气泡的线性动力学方程[24]

此处

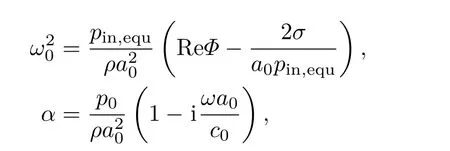
其中pin,equ=p0+2σ/a0,在多方过程假设下,Re{Φ}=3γ.为建立气泡振动与MST理论的联系,必须求解单个气泡的散射声场.在以ω为角频率的声场中,对ri处的气泡,将其散射声场写作ps(r)=fspinc(ri)G(r−ri)exp(−iωt),其中G(r−ri)=exp(ik|r−ri|)/|r−ri|是三维空间的格林函数[25],pinc(ri)为ri位置处的入射声场,ps(r)为点气泡在r处气泡的散射声场,fs为气泡的声散射幅度.对脉动气泡,根据Eular方程,有

表示了气泡散射声场和气泡径向振动的关系.考虑到气泡的径向运动可以表示为a(t)=a0[1+X(t)],且其随声场做稳态的同频率周期振动,于是有ω2X=−¨X,将其代入(3)式并结合(4)式[24],又考虑到在点源假设下ka0≪1,可以求解单个气泡的声散射幅度fs为

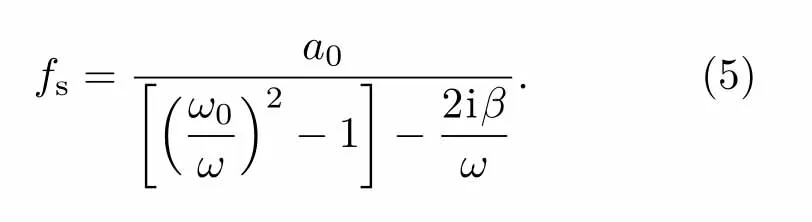
2.2 自洽方法

图1 含气泡水中的声传播Fig.1.Acoustic propagation in bubbly water.

当声波在含气泡水中传播时,每个气泡都会对声波进行再辐射,而其辐射的声波又会被其他气泡吸收和再次辐射.如图1所示,采用SCA时,忽略时间因子exp(−iωt),将气泡的声散射幅度重新写作fs(ai),其中ai为气泡i的初始半径,其相应的散射声场也重新写为pis(r,ai) =fs(ai)pinc(ri)G(r−ri).考虑到等效波数并非入射角度的函数,为简化问题,假设含气泡水内声波沿z轴传播,可将其在ri处的声压简化为

其中κ为含气泡水内等效波数,P为相应的声压幅值.由于研究对象为多分散介质,气泡半径ai也同样作为随机变量引入,各个散射体的散射幅度fs(ai)都变为随机变量的函数.

任取一个气泡j作为参考点,其空间位置变量为rj,气泡半径为aj,二者都为随机变量(图1).参考点与ri处大小为ai的气泡i的相对距离为rij=|rj−ri|.在参考点处的声压可以获得如下方程

式中pi,in为气泡i受到的激励声压,pex(rj)=εp0ejkzj为背景声场.对含有N个气泡的气泡水而言,pi,in为2N个随机变量ri和ai的函数.对参考点气泡,在(7)式两边同时求取条件期望,可得

其中〈P〉j表示气泡j的条件期望,是在参考气泡空间位置和气泡大小一定时,其余N−1个气泡的空间位置和大小的条件概率密度,其可以进一步写作气泡j一定时气泡k的条件概率密度与气泡j,k一定时其余N−2个气泡的条件概率密度的乘积f(ςN−1|rj,aj)=f(ςN−2|rk,ak,rj,aj)f(rk,ak|rj,aj). 将其代入(8)式,并假设含气泡水在空间上是统计均质的(简称均质),各个气泡的统计特征无明显差异,在此基础上(8)式化简为

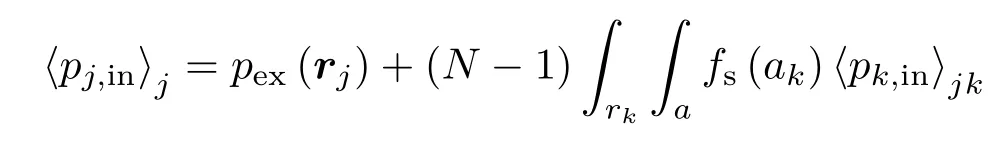
其中〈pk,in〉jk表示对气泡j,k取条件期望.对(9)式进行求解,首先给出随机变量的条件概率密度函数.相对参考点rj,大小为ak的气泡k位于drk的概率为[22,23]

其中g([rk;ak],[rj;aj])表示气泡k和j在空间上的相互影响,对均质气泡群时,g([rk;ak],[rj;aj])=g(|rk−rj|),空间影响退化为径向函数且与具体位置无关,称作径向关联函数(pair-correlation function,PCF),(10)式中气泡间的相互影响仅通过PCF表示;m(rk)为气泡群的气泡数量密度函数,在均质时退化为常数m0;n(ak)是气泡孔径的概率密度函数(这里将m0和n(ak)这两个函数区分开表示,更方便表述含气泡水的空间特性).因此,(9)式简化为

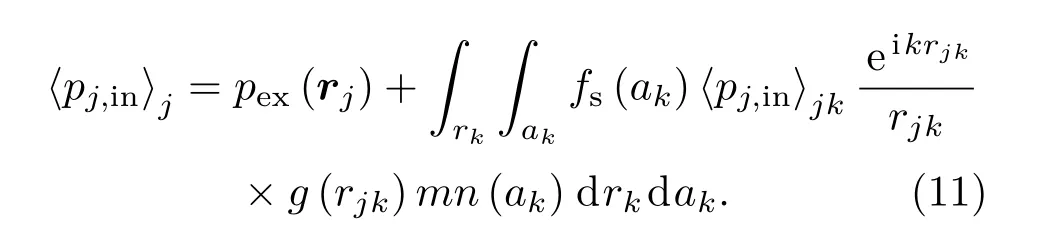
此时,在(11)式中引入QCA[26],〈P〉jk=〈P〉j,再进一步考虑气泡与含气泡水中的平均量相互作用[7−10],将〈pj,in〉j=Pexp(iκzj)代入(11)式,并去掉角标k以做化简,(11)式变换为

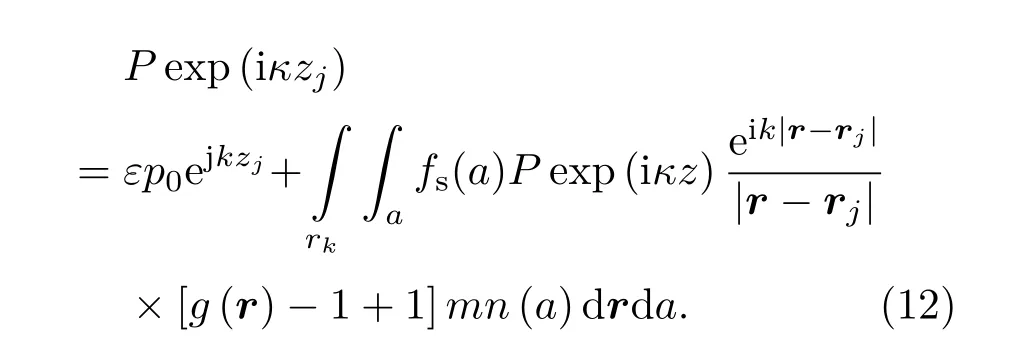
2.3 丛聚时含气泡水对声传播的影响

对丛聚的含气泡水,引入NSP对这一现象进行描述[23].采用这一方法,避免了由于气泡间的复杂受力[28]导致的含气泡水空间结构研究上的困难[29],直接给出了不同情况下含气泡水的统计特征,用统计特征建立起了含气泡水中声传播与空间分布的联系,在简化问题的基础上给出了更具一般性的结论.气泡数量密度为m的含气泡水中分布着iNSP个小范围的丛聚子气泡群,我们假设这些丛聚的成因无明显差异并在短时间内无明显变化,统计上认为这些丛聚子气泡群内空间分布相同,并在空间上整体服从Poisson分布,各自的数量密度为m0.对任意的从聚子气泡群而言,其内部仍服从Poisson分布,在空间上的一次实现中含有Nc(iNSP)个气泡.将NSP的一次实现写作

其中丛聚子气泡群nc=〈Nc〉,m0=〈iNSP〉, 且m=m0nc.本文直接给出其空间分布特征如下(数学证明可参考文献[23]),考虑到引入了QCA,因此只需要考虑二阶统计量,PCF为

这里

其中,R为气泡聚集范围的半径.将(15)式代入(13)式中,就得到了丛聚的含气泡水内的等效波数

3 数值模拟

3.1 相速度和声衰减的变化分析

在(16)式中,含气泡水中气泡空间分布的相关参数被引入到了等效波数中,在本文的数值模拟中,我们始终保持含气泡水的体积分数为5×10−4.选取边长为2.6×10−3m的观测窗,在此基础上改变nc,观察气泡空间分布对含气泡水的影响,其一次实现的x-y面侧视图如图2所示,其中,含气泡水空间分布的仿真方法在3.2节中说明.含气泡水的气泡的尺寸分布服从log-normal分布,其孔径的概率密度函数为

其中设气泡的孔径分布函数中aµ=8µm,σa=0.4,丛聚半径为20aµ.此时,注意到含气泡水小范围内的孔隙率已远大于5×10−4,那么气泡间的相互作用会对声传播产生影响,为解决这一因素的影响,进一步通过修正(5)式,考虑与背景声场的相互作用下的单个气泡的声散射能力[15]

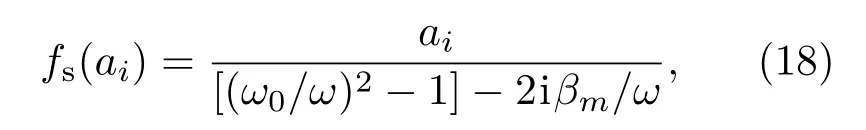
由图2可以看出,当nc较小时,直观上较难区分出含气泡水是否产生了丛聚现象,因此,在现有的实验研究中,其气泡群是否存在丛聚,是无法从直观上判断的[19−21];随着nc增长,丛聚现象逐渐明显.nc=30时,从一次实现上直观观测的结果而言,其更类似于空化产生的气泡群形成的空间球状结构,如文献[30]中图2.13中的测量结果所示.此外,观察文献[31]中图117的空化结构,如果空间网状结构中的细丝不明显存在,图2(d)也可尝试用于描述网状空化气泡群的空间结构.因此,本文的理论研究也适用于空化气泡群结构特征的研究.在此基础上,分析丛聚含气泡水对声速变化及声衰减的影响,如图3所示.

可见,丛聚现象对含气泡水内声传播的影响,主要集中在声衰减及相速度的峰值附近,对比无丛聚含气泡水可知(气泡体积分数较小且无丛聚时,本文的理论模型退化为Commander和Prosperetti[5]的结论),即使在nc=1时,其也对含气泡水的声衰减有明显抑制作用,通过对比实验结果,由图3可以看出,(16)式可以从空间信息上对现有实验结论中的偏差进行解释,即相速度和衰减系数的峰值往往低于理论预测值且存在低频偏移是由于空间不均匀导致的.此外,随nc增加,声衰减及相速度在峰值附近受到的抑制逐渐加剧,随频率远离峰值段,丛聚现象对含气泡水中声传播的影响逐渐变弱.

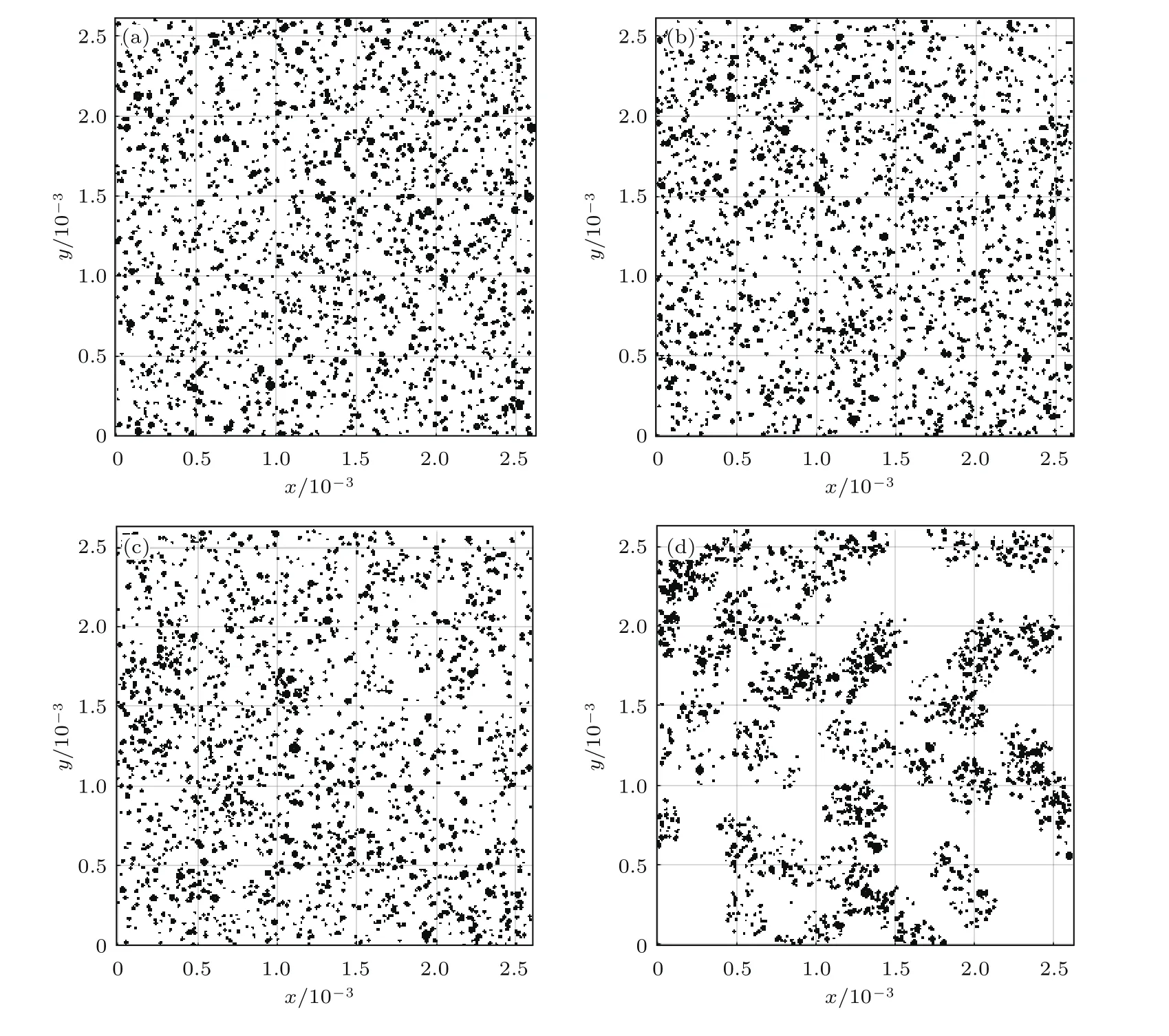
图2 不同气泡数量密度下丛聚含气泡水的一次实现的侧视图 (a)无丛聚;(b)nc=1;(c)nc=3;(d)nc=30Fig.2.Realization of clustered bubbly water with different sub-bubble number density:(a)No cluster;(b)nc=1;(b)nc=3;(b)nc=30.

图3 不同丛聚半径下声衰减及相速度随频率的变化关系 (a)声衰减;(b)相速度Fig.3.Attenuation and phase speed versus frequency with different radius of clusters:(a)Attenuation;(b)phase speed.

3.2 数值建模方法及统计分析

基于前文的结论,能否在实验中对空间信息进行有效提取,对含气泡水内声衰减及相速度的理论预测与测量结论是否拟合起到决定性作用.考虑到现有含气泡水实验研究缺乏相应的统计手段,本文引入了一种比例无偏估计以对后续实验研究进行指导.事实上,比例无偏估计既可以对(16)式中的丛聚参数测量[32],也可以对统计量自身进行直接测量[21],本节引入后一种方法,因为其更具有普遍性,在此基础上,对统计结论与理论预测的误差进行观察.

考虑到统计全部含气泡水内各个气泡的空间位置是不现实的,我们在仿真环境中也只采取其样本(后文统一称为观测窗W)进行分析.在仿真环境中,为保证考虑到W外的丛聚气泡群对W的影响,首先在扩展观测窗W⊕b(0,R)中建立丛聚子气泡群,一次实现的丛聚个数服从Poisson分布;其次,建立各个丛聚子气泡群中的气泡,每个子气泡群的气泡总数服从期望为nc的Poisson分布;最后按log-normal分布产生各个气泡的半径,就可以获得含气泡水的样本空间W,如图2所示,选取边长2.6 mm的正方形观测窗,以保证观测窗内样本气泡充足(期望值约为2000个).

为在仿真环境中建立图2所示含气泡水对声传播的影响,须对其空间信息进行提取.根据(16)式的需求,首先对其气泡数量密度进行估计,其标准估计为

其中N(W)是观测窗内含气泡总数,V(W)为观测窗体积.该标准估计是无偏的.在此基础上,对含气泡水的PCF进行统计分析,本文不加证明地引入比例无偏的PCF估计方法(具体证明过程可参考文献[21]):

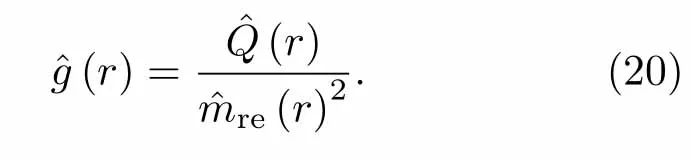
该方法通过对气泡数量密度估计进行修正保证了统计的比率无偏性(ˆmre只用于估计ˆg(r)).其中

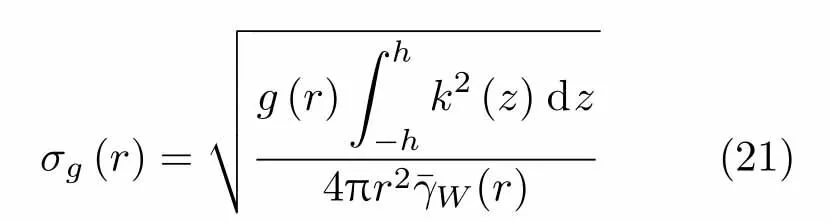
最小,将核函数表示为

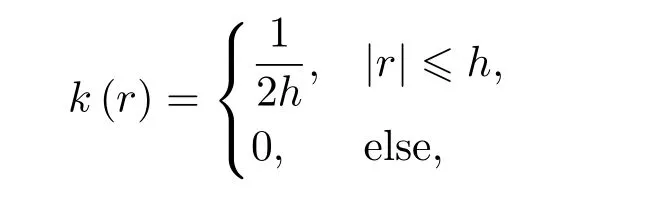
其中h为经验参数,为保证估计结果平滑且有效信息捕捉准确,本文选取h=10−5.此外,将修正的气泡数量密度写作

其中V2(W∩∂b(ri,r))表示中心位于ri半径为r的球体在观测窗内的表面积.根据(18)式及(19)式对图2(c)进行估计,可得其PCF如图4所示.

图4中红色误差棒为PCF理论值±1 MSE,将统计结果代入(13)式得到丛聚含气泡水中声速及声衰减随频率的变化,如图5所示.

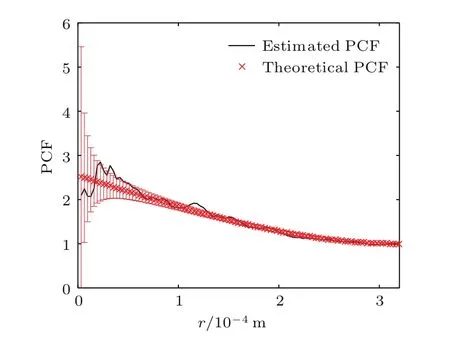
图4 PCF统计结果及误差分析Fig.4.Estimated value of PCF and error analysis.

图5 声衰减及相速度随频率变化的数值结果及误差分析(a)声衰减;(b)相速度Fig.5.Numerical results of attenuation and phase speed versus frequency comparing with theoretical value:(a)Attenuation;(b)phase speed.

以理论值求得的κ2{nc,R}做对比分析,可见当丛聚产生时,忽略空间信息会导致对声衰减及相速度的预测出现较大误差,而考虑空间信息时预测值与理论值符合良好.如果要进一步缩小考虑空间信息时仍存在的微小误差,可以通过适当扩大样本,或对观测窗进行多次采样、估计取平均值来达到目的.

4 结 论

含气泡水的空间结构是复杂的,自然现象产生的含气泡水中的气泡很难保证均匀分布.在实验室环境下,含气泡介质内气泡间也常存在小范围的聚集趋势,而现有描述水下气泡群对声传播影响的理论往往基于空间均匀分布假设.因此,当含气泡水存在聚集时,现有理论描述声波在含气泡水中的传播时存在较大误差.为分析非均匀分布的含气泡液体对声波线性传播的影响,我们将QCA引入自洽方法中,推导出了考虑空间分布时多分散介质中的等效声波波数,在此基础上引入NSP描述了含气泡水内气泡的丛聚现象.分析发现,即使直观上无法观测到的丛聚现象,也会对含气泡水内声传播产生较大干扰,因此含气泡水的空间信息不可忽视.

通过本文给出的数值仿真方法,可观测到丛聚的含气泡水对声衰减及相速度的准确预测影响较大,忽略空间信息会过高估计声衰减及相速度的峰值,因此,在进行相应的实验研究中必须对空间信息进行有效提取,而本文的建模及比例无偏估计方法可作为相关实验工作的理论基础.