含几何缺陷金属管失稳外压计算模型的优化分析
2018-09-21魏晨杨阳
魏 晨 杨 阳
(1.四川建筑职业技术学院土木工程系,四川德阳618000;2.四川建筑职业技术学院电气工程系,四川德阳618000)
0 引言
在外压作用下,导致管道发生失稳的因素中,除管道残余应力、管道轴向载荷外,管道截面椭圆度也是一个重要因素。实验表明,椭圆度会使管道失稳压力最大下降约25%。管道残余应力、管道轴向载荷对管道失稳产生的影响,可依据API-5C3标准进行判断,而椭圆度对管道失稳产生的影响,尚未有可靠的理论依据,因此提出一个能够准确描述椭圆度与管道失稳关系的模型是非常必要的。现有的管材在椭圆度影响下失稳外压计算模型在提出过程中做了一些限定条件及假设:以点压力代替面压力、压力计算过程中忽略管道径厚比,从而导致模型分析结果与实验结果相比过于保守,模型的实际指导意义有限。一个更为可靠的管道失稳评判模型应在保障管道使用安全前提下,以尽可能提高管道使用率为目标。因此有必要对椭圆度影响下管道失稳模型进行优化处理,满足安全与使用两方面的要求。
1 椭圆度影响下管道失稳外压计算模型
模型计算得出的失稳压力保守的原因主要有两方面:首先弯矩项最初带有指数,为方便失稳压力的计算,将弯矩项指数去掉,即忽略管道径厚比可能带来的影响,这会导致计算的失稳压力比实际的小;其次由于管道截面的椭圆化,管道截面各个点的失稳压力是不同的,用危险点失稳压力代表整个截面的失稳压力,得到的管道失稳压力也比实际的小。因此提高模型可靠性可从上述两方面着手。
2 从数学角度对模型进行修正
椭圆度影响下管道失稳是一个多因素问题,目前存在可参考的类似模型是管道在弯曲与外压共同作用下的失稳问题。从管道在弯曲与外压共同作用下的失稳模型出发,利用材料力学中弯矩与曲率的关系、曲率与椭圆度的关系,得到椭圆度影响下管道失稳压力计算模型:
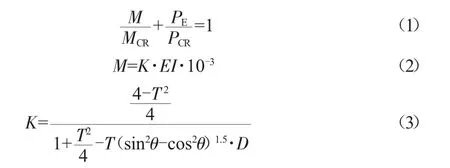
式中,M为一定椭圆度对应的弯矩(N·m);MCR为管道仅在弯曲作用下临界失稳弯矩(N·m);PCR为管道仅在外压作用下临界失稳外压(MPa);PE为待求失稳压力(MPa);K为一定椭圆度对应的曲率,无量纲数;T为管道截面椭圆度,无量纲数;D为管道外径(mm)。
模型计算得出的失稳压力较为保守的原因主要有两方面:(1)模型(1)中弯矩项最初带有指数,将弯矩项指数去掉,即忽略管道径厚比可能带来的影响,这会导致计算失稳压力比实际小;(2)由于管道截面的椭圆化,管道截面各个点的失稳压力是不同的,式(1)得到的是管道危险点的失稳压力,即用危险点失稳压力代表整个截面的失稳压力,得到的管道失稳压力也比实际小。因此提高模型可靠性可从上述两方面入手。
现有计算模型指数中包含了管道径厚比与失稳压力,较难直接进行求解,故需要在大量实验基础上对指数项进行试算,使得指数项在相应条件下成为一个仅与径厚比有关的常数。大量直接的实验数据表明:(1)当管道径厚比在10~20之间时,径厚比对其值的影响有限;(2)当管道径厚比大于20时,管道属于大口径薄管壁管道,发生失稳的概率大大增加;(3)椭圆度平均会使得管道失稳压力为理想情况下压力的80%左右。
(1)径厚比在10~20之间:

(2)径厚比大于20时:
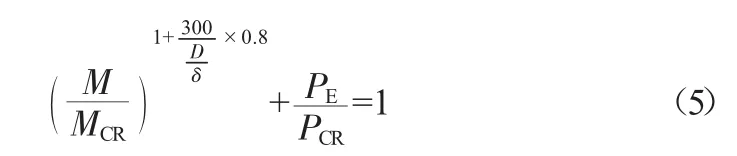
为了验证模型可靠性,计算管径为40 mm、径厚比为12.8情况下的模型失稳压力并与实验失稳压力进行比较。试验样本材料为Q235,屈服强度为235 MPa,杨氏模量为200 GPa,由API-5C3标准得出管道仅在外压作用下的失稳压力PCR,将椭圆度、截面各点处曲率输入模型得到管道截面各点处弯矩及管道失稳压力(表1)。

表1 初次修正后模型失稳压力与实验失稳压力比较
修正后模型计算失稳外压约为实验失稳外压值80%,修正前模型失稳外压约为实验失稳外压值的60%。说明通过对模型的修正显著提高了模型的实际指导意义,提高了管道材料的利用率,但同时模型保留了一定的安全裕度,保障了管道的使用安全。
3 从力学角度对模型进行优化
模型中通过曲率引入椭圆度,同时曲率项中包含标定管道截面具体位置的角度项θ,由曲率的表达式及模型(3)我们可以看出当角度取0与π时,即在管道截面的长轴处管道的失稳压力最小,管道截面长轴处最先发生失稳,故长轴处为管道截面的失稳危险点。模型(1)用管道截面危险点的失稳压力代表整个截面的失稳压力,一定程度上存在误差,这里在大量实验的基础上,用截面管道利用率期望作为管道的截面系数β,取代曲率项中的角度项θ,进而得到整个截面的失稳压力来描述椭圆度对管道失稳的影响。
假设管道在椭圆度影响下管截面是标准椭圆,故根据对称性只研究角度在0与π/2之间的情况,分布点的选择按照近长轴处紧密,近短轴处稀疏的原则选取,选择0°、30°、45°、90°。截面系数的可靠性与实验数据量的多少以及分布点的选择正相关,在各个点处的失稳压力计算方法与前面相同(表2)。
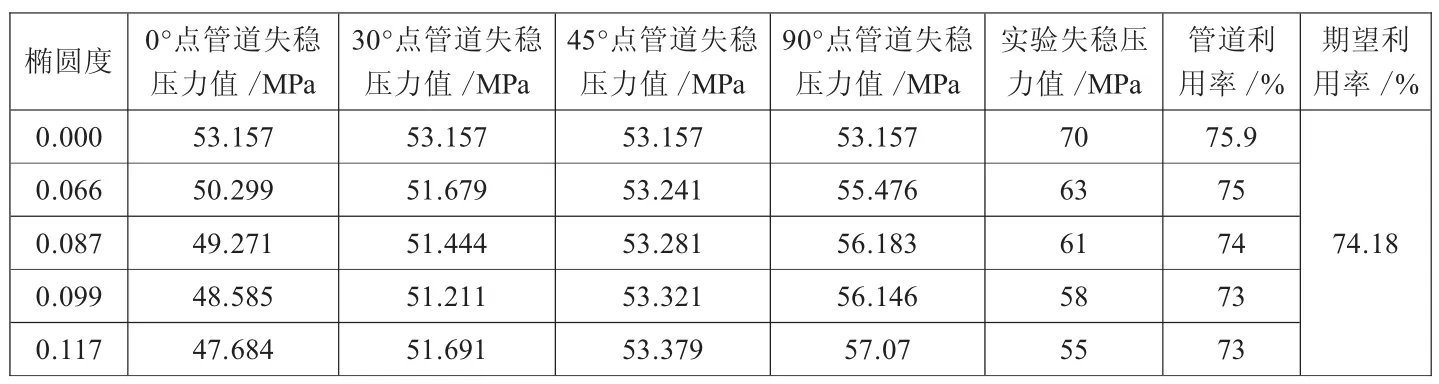
表2 管道截面分布点失稳压力
由表2得出β=0.741 8,这样曲率的表达式改写为:
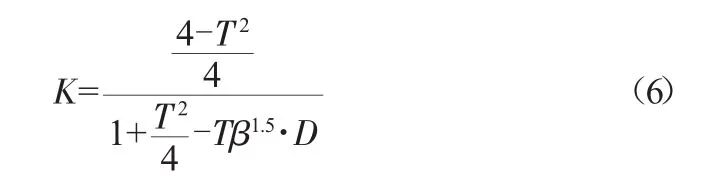
为了验证截面系数的可靠性,计算管径为40 mm、径厚比为12.8的模型失稳压力并与实验失稳压力进行比较。试验样本材料为Q235,屈服强度为235 MPa,杨氏模量为200 GPa,由API-5C3标准得出管道仅在外压作用下的失稳压力PCR,根据材料力学知识得出管道仅在弯曲作用下的失稳弯矩MCR。将椭圆度代入(6)得到相应椭圆度管道截面各点处曲率,将曲率代入(2)得到管道截面各点处弯矩,将弯矩代入优化后计算模型(4)得到最终管道失稳压力(表3)。
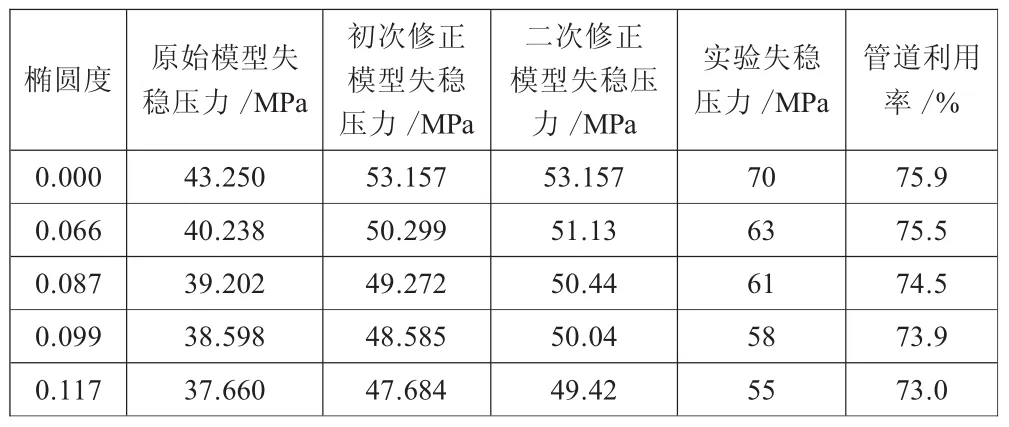
表3 二次修正后模型失稳压力值与实验失稳压力值比较
用截面失稳压力代表截面危险点失稳压力,可进一步提高管道使用效率,但效果很有限,这与截面系数β有关,截面系数β依赖于实验数据量,可靠的β建立在大量实验数据的基础上。利用计算机编程功能得到更多分布点失稳压力,可获取更为全面的截面系数。
4 结论
(1)由图1可知,在原始模型基础上,通过引入管道径厚比使得模型失稳压力较原始模型失稳压力可靠性显著提高,且可靠性随着椭圆度的增大而增大,这说明初次优化后该模型能够作为评判管道在椭圆度影响下失稳的理论依据。
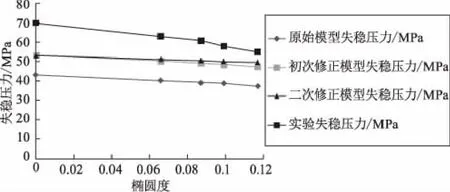
图1 原始模型与各级优化模型效果对比
(2)在初次优化的基础上通过引入截面系数,以截面失稳压力代表管道失稳压力这一思路得到最终优化模型。随着椭圆度的增大最终优化模型相较初次优化模型在可靠性及相较实验失稳压力的误差方面的优势显现出来,说明引入截面系数更加符合客观事实,但其实际对模型的优化效果有限,这与管道截面系数的选取有关,要使截面系数更加具有普遍适用性,就必须建立在大量实验数据上或是依靠计算机寻找截面系数。
