绳索式3D驱动装置原理与算法

杨一通 王树国 严卫庆 张骏杰 赵 辉

（东北林业大学，黑龙江哈尔滨150040）

0 引言

3D驱动在人们的生活中有着广泛的应用，最常见的3D驱动装置为“天车式”驱动装置[1]，图1为工程天车简图。工作平台首先在两根轨道梁上进行x轴方向的运动，其次进行垂直于轨道梁的y轴方向的运动，最后进行z轴方向的运动，从而实现3D驱动。“天车式”3D驱动在吊装、3D打印等众多领域都有所应用。

图1 工程天车简图

“三角爪式”3D驱动应用在三角洲系列3D打印机等装置中，如图2所示。工作原理为三个步进电机通过齿条带带动三组滑车在三根立柱上进行竖直运动。三组滑车分别通过三组连杆与工作平台连接，从而实现对工作平台的3D驱动[2-3]。

本文所研究的绳索式3D驱动装置，以“三角爪式”3D驱动装置为基础，建立新的三角形框架结构，将带动平台运动的连杆用绳索加以替换，通过对程序的重新改写，进而实现通过绳索对工作平台进行3D驱动[4]，形成结构简单、成本低、大范围运动的3D平台。

1 绳索式驱动装置硬件结构的设计

绳索式驱动装置包括机架、电路控制板、步进电机三个、容绳机构三组、滑轮三组、绳索三组、工作平台一套，如图3所示。三组步进电机接收到程序信号，分别带动各自的容绳机构，通过控制绳索的长度，对工作平台进行空间驱动。电路控制板通过连接线与计算机相连接，通过在Cura[5]软件输入目标图形或路径后运行，便可带动工作平台进行3D驱动。

图2“三角爪式”3D打印机机架模型

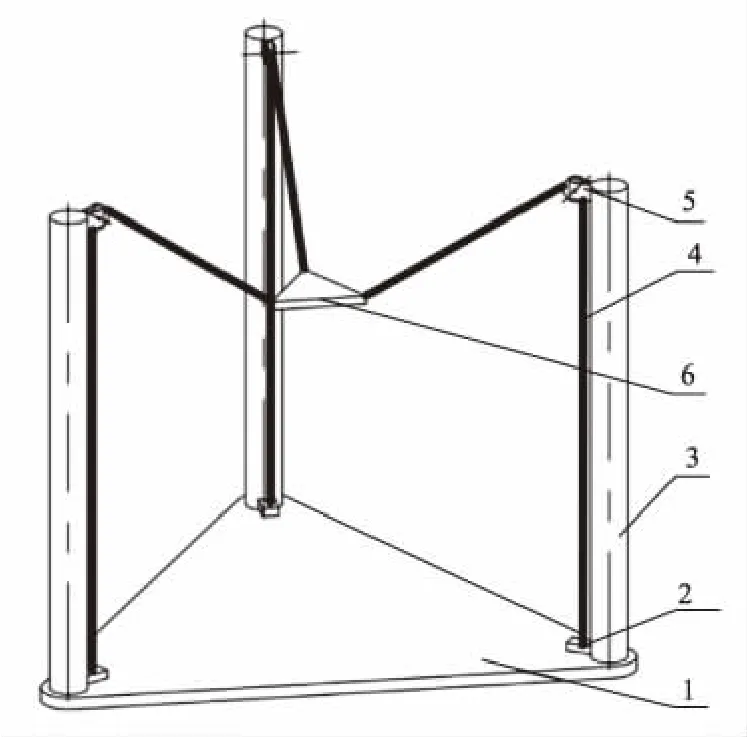
图3 装置示意图

2 绳索式驱动装置的算法设计

装置的电路控制板采用Arduino Mega 2560开发板[6]，程序以3D打印机Marlin固件[7]为基础重新进行编译。

2.1 驱动装置算法空间坐标系的建立

首先，在空间直角坐标系任取xOy平面上方三点A、B、C，连接AB、BC、AC，形成△ABC。将△ABC投影到xOy平面为△A1B1C1，A、B、C三点到xOy平面的距离分别为h1、h2、h3。

令BC、AC、AB边长分别为a、b、c，B1C1、A1C1、A1B1边长分别为a1、b1、c1，如图4所示，则有关系：

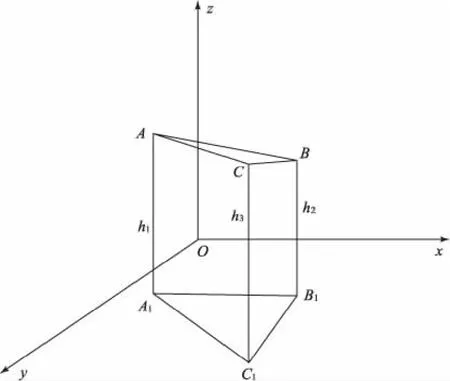
图4 空间坐标关系示意图

我们以△A1B1C1的外接圆的圆心为坐标系原点O，以过圆心且平行于B1C1边的射线作为坐标系的x轴建立平面直角坐标系，此坐标系也为程序所用坐标系。设B1C1与y轴的交点为P，如图5所示。

图5 平面坐标关系示意图

根据正弦定理及余弦定理，可以计算出外接圆的半径R为：

根据坐标系中的三角关系，有如下关系：

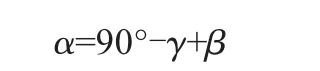
则在程序坐标系下：A1坐标为（Rsin α，Rcos α），B1坐标为

在坐标系的确立上，空间任意三角形定义到固件的主要参数为A、B、C三点到xOy平面的距离h1、h2、h3和△ABC的各边长a、b、c，以及角1的正弦值sinα与角α的余弦值cosα，共计8个参数。

2.2 驱动装置运动关系的构建

“三角爪式”3D打印机与其他打印机的区别在于“三角爪式”打印机的程序中有一个笛卡尔坐标系的转换函数，该函数位于控制打印机运动的核心部分Process_commands()中。在Process_commands()中，主要含有get_coordinates()和prepare_move()两个子程序以及一个计算目的坐标的程序段。

get_coordinates()的主要功能是获取被控制点当前所在位置的坐标，即当前坐标。计算目的坐标的程序段是根据计算机所得到的指令计算出被控制点所要达到的下一点的位置坐标，即目的坐标。prepare_move()的主要功能是根据获得的目的坐标和当前坐标控制步进电机运动。而在子程序prepare_move()中含有子程序calculate_delta()和plan_buffer_line()。其中calculate_delta()是将被控制点的坐标变化转换为步进电机的运动量，而plan_buffer_line()则根据calculate_delta()输出的结果控制电机运动。对于Process_commands()的主体流程，可用如图6所示流程图表示。

图6 主体程序流程图

本驱动装置是将传统的控制平台运动的连杆改为柔性绳索。所以，若要完成该创新改造，除需要对硬件进行改造外，还需进行控制算法的重新编写[8-10]。由于连杆结构被改成了绳索，所以其空间位置坐标改变量转换为步进电机运动量的方式发生了改变，这就要求我们对calculate_delta()的函数进行重新编写。

传统的机构是连杆传动，其结构关系如图7所示，其中l是连杆长度，为定长。

图7 连杆式杆长关系

运算关系为：

经过理论分析和数学推理发现，与电机和工作平台相连的柔性绳索与被控制点满足如图8所示的关系。

其中总绳长l′为定值，分为步进电机到滑轮的绳长l1′和滑轮到工作平台的绳长l2′。

图8 绳索式绳长关系

运算关系为：

因l1的变化量即步进电机的运动量，所以将calculate_delta()的输出值定为l1，则plan_buffer_line()即可控制步进电机根据指令运动。

运动关系程序语句如下：

delta[X_AXIS]=DELTA_STRING_LONG-sqrt(sq(DELTA_TOWER1_X-cartesian[X_AXIS])+sq(DELTA_TOWER1_Y-cartesian[Y_AXIS])+sq(DELTA_TOWER_Z-cartesian[Z_AXIS]));

delta[Y_AXIS]=DELTA_STRING_LONG-sqrt(sq(DELTA_TOWER2_X-cartesian[X_AXIS])+sq(DELTA_TOWER2_Y-cartesian[Y_AXIS])+sq(DELTA_TOWER_Z-cartesian[Z_AXIS]));

delta[Z_AXIS]=DELTA_STRING_LONG-sqrt(sq(DELTA_TOWER3_X-cartesian[X_AXIS])+sq(DELTA_TOWER3_Y-cartesian[Y_AXIS])+sq(DELTA_TOWER_Z-cartesian[Z_AXIS]))

3 装置运行实验结果

实验装置是在等边三角形机架的基础上建立的，建立好的装置如图9所示。应用Cura软件分别进行了圆环（半径为6 mm）和直线打印工作，记录方式采用工作平台搭载激光笔，对工作过程进行视频录制，将激光笔走过的轨迹在坐标纸上描绘，把相应的点输入到Matlab软件中拟合成圆和直线，如图10和图11所示，并存有相应部分的视频文件。

图9 装置实物图

图10 圆的拟合图

图11 直线拟合图

通过图中这两组具有代表性的数据可以看出，运动轨迹较为圆滑平稳。在打印头从初始位置降落到打印平台的过程中，由于振动较大，导致前面的几个点误差有较大波动。终止点由于惯性的作用，也有较大的误差。总体误差为毫米级。

4 结语

通过本文可以得出以下结论：绳索式3D驱动装置可以实现对工作平台的3D驱动。装置可根据现场情况，将电机安置于建筑物或者其他稳固物体上。工作台可根据工作需要，搭载不同的机械装置（例如打印喷头、机械手臂、电磁铁、搜寻装置等）进行3D打印、智能分拣、搬运以及搜寻工作。相比于传统的固定式工作台有灵活性高、适应性强、可用范围广以及成本低等特点，可大幅度降低劳动成本，提高劳动效率。