MapReduce背景下的复杂网络链路预测分析
2018-09-21常雅文
常雅文
(西安航空学院, 西安 710077)
0 引言
复杂网络链路预测由于在社交网络、信息通信等社会方面的广泛应用,现已成为数据挖掘的主要研究方向,已成为学术界关注的热点[1]。网络链路预测作为一种预测方式主要是通过已知网络拓扑结构和网络节点属性等信息预测网络中未产生连边的节点产生连接的可能性[2]。传统的链路预测算法以节点属性为特点,譬如马尔科夫链或机械学习等算法,尽管算法预测精度高,但由于计算复杂度高、计算中涉及的非普适性参数应用的限制,导致算法使用受限[3-4]。另一类传统链路算法则以网络结构为特点进行最大似然估计,文献[5]中介绍了一种网络层次结构为基础的链路预测算法,并显示该类算法在层次结构明显的网络中具有较高的预测精度,但该类算法的计算复杂度高。
与传统的链路预测算法相比,以网络拓扑结构为基础的链路预测算法通用性强,且网络拓扑结构极易获得。但在处理大规模复杂网络链路时,由于算法复杂度和单台计算机内存限制,处理速度慢,且准确性不足。MapReduce[6]作为Google公司2004年提出的可以并行处理海量数据的编程模式和任务调度模式,可以通过屏蔽底层实现细节减少并行编程复杂度,提高编程效率而具有广泛应用。基于MapReduce编程时,开发人员只要考虑应用程序本身特性,无需考虑集群处理,将其交由平台处理。因此在MapReduce背景下进行复制网络链路预测分析具有重要的使用价值和意义。由于MapReduce模型并不允许任意读取图中的节点以及边信息,因此本文基于节点局部信息的相似性指标进行复制链路预测分析。
1 MapReduce背景下的复杂链路预测算法
1.1 问题描述
记G(V,E)为一个无向网络,其中V和E分别代表节点集合和边集合。总的节点记为数为N,则节点对数为U=N(N-1)/2。对于两个节点,在相似性框架下,其产生链接的可能性与相似程度成正比,即相似程度越高,产生链接的可能性越大。同样,给定度量节点相似性指标,则复杂链路预测问题会转变成为一个无监督学习问题,即:对于给定的网络数据集G,依据相似性指标计算获得网络中每两个节点间的相似值,行程相似矩阵,依照相似值排序,获得两节点间产生链接的概率排序。本文定义的相似性链路预测在度量节点的相似性时,主要从网络本身拓扑结构出发分析,未考虑其他由于网络特殊性,譬如社交网络中表示节点拥有用户个性化兴趣等,造成的节点自身属性,这也是本文问题描述与其他有监督学习方法的区别。
以局部信息为基础的链路预测算法有10种,具体相似性指标定义公式,如表1所示[7]。

表1 基于节点信息的10种相似性指标
网络节点表示为x,其节点的邻居表示为Γ(x),而k(x)=|Γ(x)|则代表节点的度,Sxy则代表点对(x,y)的相似性。相对于另外9种指标,PA指标不包含共同邻居信息,为保证信息一致性,本文只考虑代表的指标CN、RA和AA。
1.2 MapReduce 并行计算模型
目前关于MapReduce并行链路预测算法的应用,主要在Hadoop平台[8]上进行。Hadoop属于分布式系统平台,包括分布式文件系统HFDS以及核心算法MapReduce。MapReduce包括两个阶段,即:Map阶段和Reduce阶段。Hadoop首先进行输入数据分片,将其形成多个小数据块,然后Map执行相关任务,Reduce则执行将Map阶段获得中间结果汇总输出。具体执行过程,如图1所示。
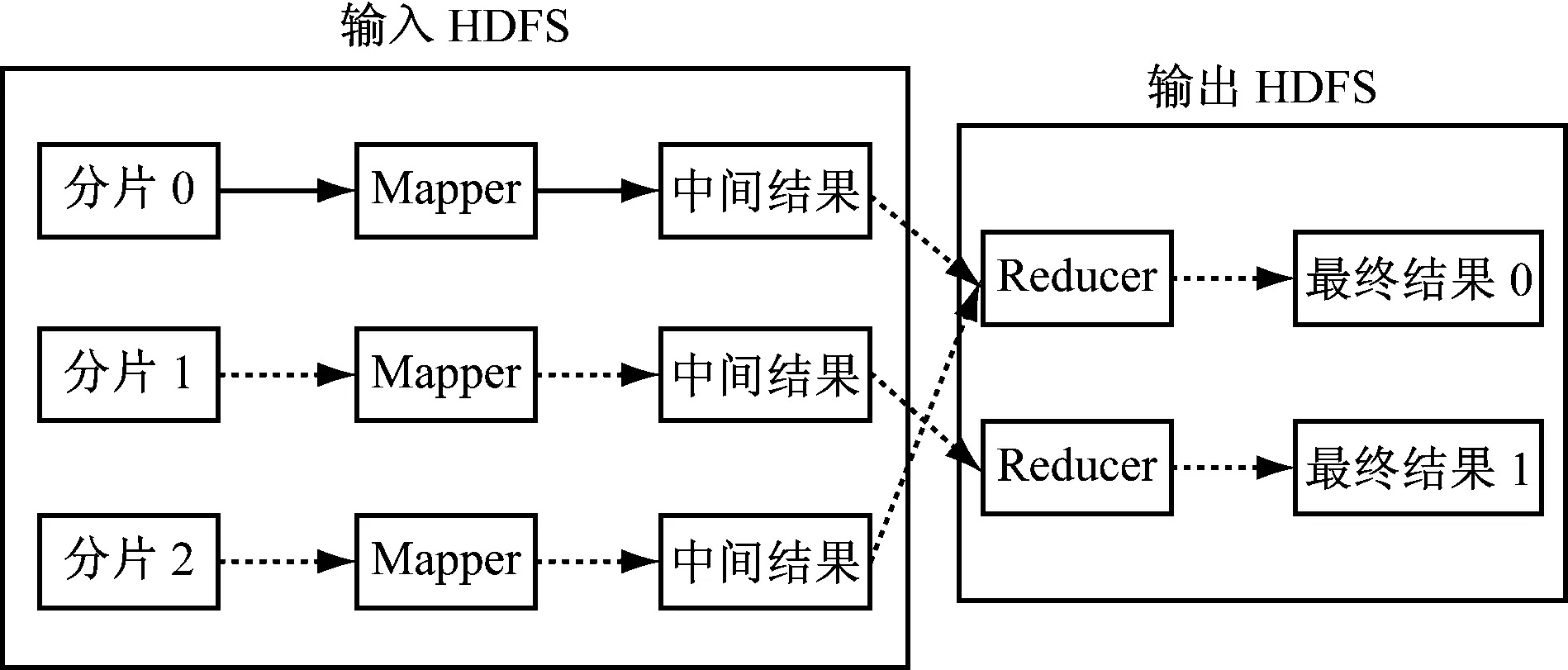
图1 具有多reducer任务的MapReduce数据流
(1) 预处理:MapReduce首先调用类库,将输入文件等大小(64MB)划分几个分片;
(2) 分配任务:JobTracker(负责对整个作业执行进行调度,一个集群只含有一个)为集群中空闲节点分配Map或Reduce任务;
(3) Map任务:Mapper读取文件分片,并转换成
(4) 确定缓存文件位置:周期性的将中间结果写入Mapper对应的本地硬盘,并将存储地点发送给Reducer;
(5) 利用Reducer获得Mapper拉取文件:利用位置信息,得到Mapper处拉取的文件。当所有临时结果被读取完毕,将所有相同key中所有value合并成一个组,获得
(6) Reduce任务:Reducer将所获得的
(7) 结束:当所有Map和Reduce运行完毕后,系统会通知用户并进行信息报告。
1.3 利用MapReduce 分析复杂网络链路预测
利用MapReduce并行计算模型实现排除基于节点局部信息的CN、AA、RA相似性指标,这3种指标应用到了节点的共同邻居信息,因此,在并行算法上具有一致性,基于MapReduce并行计算模型的复杂网络链路预测算法步骤如下:
输入:G(V,E)的边集E(文件A);
输出:AUC值(曲线下面积,通过AUC超过0.5的大小衡量链路预测算法的准确性)。
步骤一:得到网络节点数N,并将网络边集E分割形成训练集ET(文件B)和测试集EP(文件C)。
步骤二:获得ET和EP中边个数,获得ET中所有节点度。
步骤三:将ET中点对用邻接表表示;
步骤四:对于ET的邻接表,利用相似性指标获得两两点对的预测分数值(文件D);
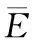
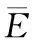
(1)
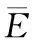
对于步骤四种中利用相似性指标获得两两点对的预测分数值的方法如下。
Mapper
输入:图G(V,E)的邻接表;
输出:图G(V,E)两两点对之间的共同邻居。
具体流程图,如图2所示。

图2 Mapper流程图
Reducer
输入:图G(V,E)两两点对之间的共同邻居;
输出:图G(V,E)两两点对之间的预测分数值。
具体流程图,如图3所示。
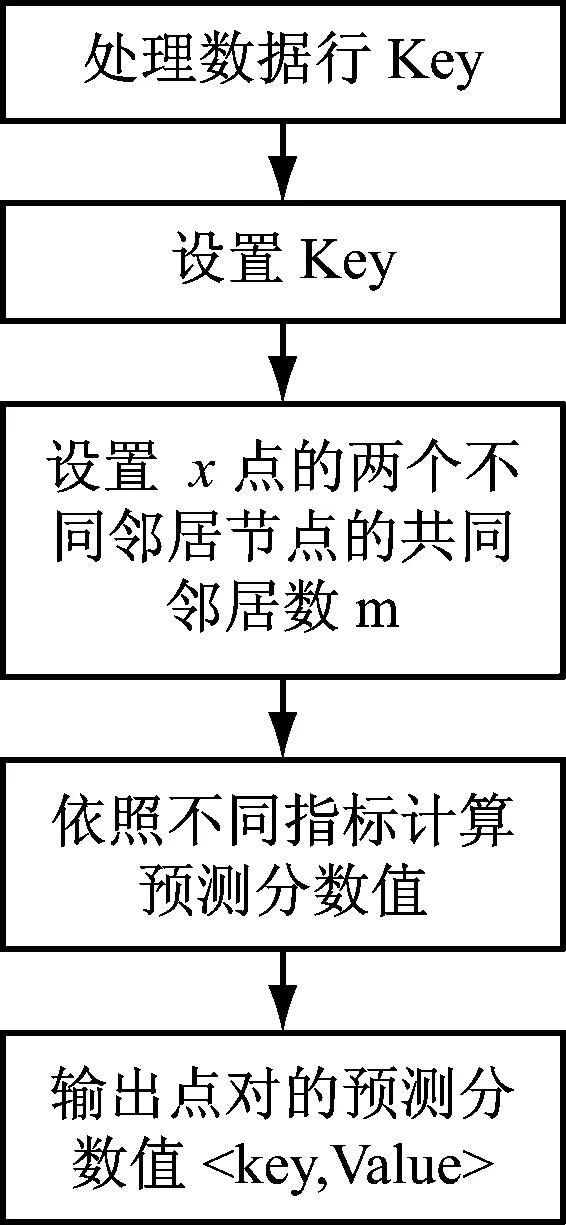
图3 Reducer流程图
2 实验结果及分析
2.1 实验设置
为验证MapReduce并行链路算法的精确度,本文选用6个不同类型的网络,包括社交网络、信息网络和生物网络等,与3种其他链路预算进行对比。选用的数据集有[10]:Jazz网络,爵士乐音乐家的一个合作网络,节点数为198个,其中每个节点代表一个音乐家,节点之间的边代表音乐家之间的合作关系;Celegans网络由watts等人汇编,属于生物网络类型,节点总数为297,每个节点代表一个神经元,边则表示神经元突触; Yeast属于酵母菌蛋白质交互(PPI)网络,属于生物网络,一个节点代表一个酵母菌蛋白质,边代表蛋白质间的相互作用;Power网络属于电力网络,节点表示发电站、中转站等,边代表高压传输线;Router网络作为一种信息网络,代表了路由器层面的计算机网络,节点表示路由器,边代表路由器之间的物理通信线路;USAir作为美国一个航空网络的数据集,节点表示航空港,边表示航线,该网络包括两千多条边,属于信息网络类型。
为6个网络的相关拓扑特性,如表2所示。

表2 不同网络基本拓扑特征比较
其中聚类系数表示网络聚类特性描述指标,聚类系数越大,代表网络社团的特征越明显;网络直径代表所有节点对的直线距离最大值;平均刻度表示节点度数的平均值。节点数越多,则平均度越小,代表网络越稀疏,节点之间联系不紧密,因此聚类系数低,网络直径大。
2.2 实验结果
对复杂网络链路预测效果采用AUC指标进行评估,在式(1)中,将复杂网络分为训练集和测试集,两者比例为9∶1,通过训练集计算获得各网络中每两节点之间的相似度分数后,每次随机从测试集和不存在的边集中分别选取一条边进行比较。若测试集中边的相似度分数值超过不存在边的相似度分数值,加1分;若两个相似度分数值相等,则加0.5分,以上独立比较N次。假设所有分数均随机产生,则获得的AUC=0.5,各种并行链路算法获得AUC值超过0.5的程度衡量了算法比随机选择准确的程度。
为不同链路预测算法的AUC评价结果,如表3所示。

表3 不同链路预测算法的AUC值
由此可见,在选取的6个不同类型的真实网络中,基于共同邻居的相似性算法基本都获得了0.8以上的链路预测AUC效果。将MapReduce背景下的复杂网络预测所得的AUC值与文献[11]中基于节点相似性的复杂网络链路预测所得AUC结果对比发现:MapReduce背景下的复杂网络预测所得的AUC值与普通条件下基于节点相似性的复杂网络链路预测所得AUC基本保持一致,误差在0.035,属于可接受范围内。
2.3 分析及讨论
实验中观察到如下现象:针对不同网络,每个算法的效果差距较大,对于CN算法,AUC结果从0.86到0.95不等,性能差异高达11%;并且每个算法其性能差异是以同样的规律波动,网络平均度对应的各个算法性能差异示意图,如图4所示。

图4 网络平均度对应的各算法性能
结果显示:选取的各个参照算法的性能基本上是按照同样的规律在波动,这显示共同邻居越多,相似性越大。
3 总结
针对MapReduce的特点,发现其可以有效规避传统并行链路算法存在的计算机复杂度高和单个计算机内存现在问题,将MapReduce应用于复杂网络链路预测分析具有重要的意义。本文主要基于MapReduce背景下进行复杂网络链路预测分析,结果显示:MapReduce背景下的复杂网络链路预测分析有效,且选取的各个参照算法的性能基本上是按照同样的规律在波动。
