基于计算流体动力学的两栖车辆水动力性能模拟及试验验证

蔡宇峰,王丽丽,汪 宇,徐永泽

(1.中国特种飞行器研究所,湖北 荆门 448035; 2.江麓机电集团有限公司,湖南 湘潭 411100;3.西递安科软件技术有限公司(上海),上海 200120)

水陆两栖车辆是同时具有陆地车辆性能和水上船舶性能的一种特殊车辆,既可以在陆地上行驶,又可以泛水浮渡。水陆两栖车辆具有船舶的特点,但不具有船舶的局限[1-2]。目前针对水陆两栖车辆水动力性能的研究方法,基本上是参照船舶设计中的拖曳试验方法。该方法虽然可靠性强,但是成本高、周期长。随着船舶计算流体动力学(CFD)技术的发展,使得采用数值计算方法研究两栖车辆的水动力特性成为可能[3-7]。

两栖车辆作为一种特殊船体,其水上性能与船舶有很大的相似性,因此参照船舶领域的研究方法是有必要的。20世纪70 年代以后,基于CFD的流场分析技术受到了船舶领域的高度重视。近年来,一些研究者采用数值计算方法对两栖车辆的绕流场进行了数值模拟。高富东等[8]利用CFD研究车体首端和尾端切角并对车辆外形进行优化,减阻效果达到了51.2%。王涛等[9]基于CFD计算了典型的两栖车辆迎浪直航运动。黄劲等[10]基于CFD将计算所得水动力导数与船舶经验公式值进行对比,分析了两栖车辆与船舶的差异对水动力导数造成的影响。

本文通过对某型两栖车辆实车和模型静水三自由度运动进行模拟,以及采用模型试验对仿真值进行验证,分析了两栖车辆实车与模型之间的水动力性能换算关系。基于CFD理论建立了两栖车辆带自由液面黏性绕流场的数学模型,采用Realizablek-ε两方程湍流模型、流体体积法及重叠网格对两栖车辆绕流场进行三维瞬态数值计算,得到绕流场、阻力、纵倾与升沉。模型试验在中国特种飞行器研究所高速水动力实验室的拖曳水池进行。

1 实车及模型的仿真模拟

1.1 研究对象

本文的研究对象是水陆两栖车辆的实车及模型,研究对象参数如表1所示。研究过程中车辆没有履带,只有车轮。

表1 两栖车辆参数Tab.1 Parameters of amphibious vehicle

1.2 数值水池及数值处理方法

在进行仿真模拟时,先将姿态角抬高5°,实车自由液面降低0.2 m,这样调整可以使计算状态提前稳定。车体运动求解采用DFBI (dynamic fluid body interaction)刚体运动模型。该模型将车体视为空间中的六自由度运动刚体,在流体压力、摩擦力、重力及其他外力的作用下发生平动及转动。 在求解过程中,主要关注重心的移动及绕重心的纵倾角度。

按照相似理论,来流方向两栖车辆不动,流体在入口以固定速度流入。入口距离车身首部1L(L为车体长度),该入口为速度入口,水线上方为气相入口,水线下方为液相入口;出口距离车身尾部3L,该出口为压力出口,压力随水深变化而变化。上边界、下边界距离车身均为1.25L,设置为速度入口。侧边距离车身1.5L,设置为对称边界。由于静水航行流场关于中纵剖面对称,因此仅对流域一半进行网格离散,中纵剖面设置为对称边界。计算时先采用整体运动网格,在计算过程中发现车身姿态变化显著,容易发生自由液面移动出网格加密区的情况,从而导致计算精度大幅降低。针对此问题,采用重叠网格,从而保证了模型在大角度姿态时自由液面的加密区网格不发生移动。采用流体体积法捕捉自由液面,该方法可以处理空气和流体具有交界面的稳态和瞬态等问题。

1.3 数值结果及流场分析

表2分别给出了实车及模型的仿真计算结果,缩尺比为2.5。表2中,实车仿真值记为A;根据弗劳德数相似的换算方法,把A换算成模型仿真值,记为B;模型仿真值记为D。速度、阻力、实际姿态、升沉的换算比例分别为λ0.5、λ3、1、λ,λ表示实车与模型间的升沉比例关系。从表2可以看出,B与D两者存在误差,但是差值不大,进一步验证实车与模型之间在一定程度上可以采用船舶的弗劳德数相似的换算方法;计算域内网格的精细程度及计算步长会导致B与D之间存在误差。

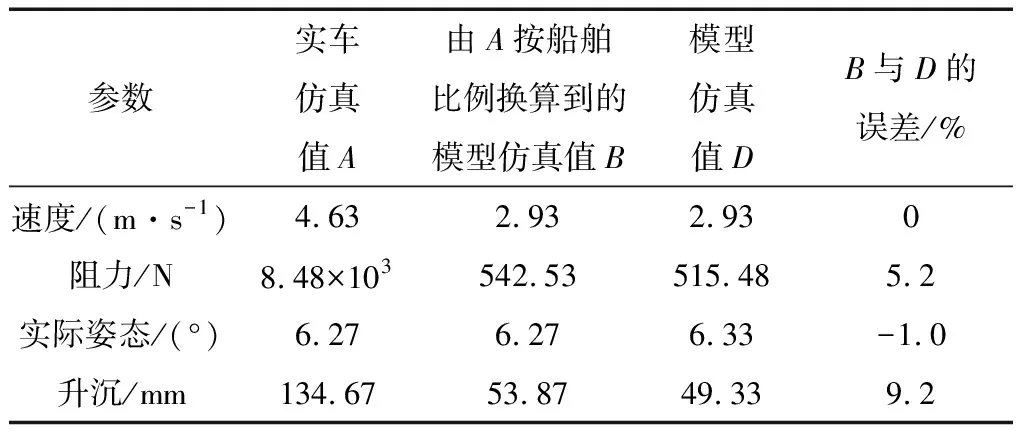
表2 实车仿真值及模型仿真值Tab.2 Numerical results of all scale car and model

如图1～3所示,车体尾部后方水面下降,车辆陷入由自身运动而形成的盆状空间内,整体车辆尚未因滑行而完全托出水面。水陆两栖车辆设计需要考虑车辆的陆地行驶性能,因此车体曲度变化较突然。在两栖车辆车体曲度骤变处,特别是车体的尾部常会产生漩涡,越靠近漩涡中心压力越低,从而形成吸力,此吸力阻碍了两栖车辆的前进。水陆两栖车辆在水上运动过程中会掀起波浪,由于波浪的产生,改变了船体表面的压力分布情况。车首的波峰使首部的压力增加,而车尾的波谷使尾部压力降低,于是产生首尾流体动压力差,进而形成阻力,压差阻力占两栖车辆总阻力的绝大部分。

图1 实车自由液面Fig.1 Free surface of all scale car

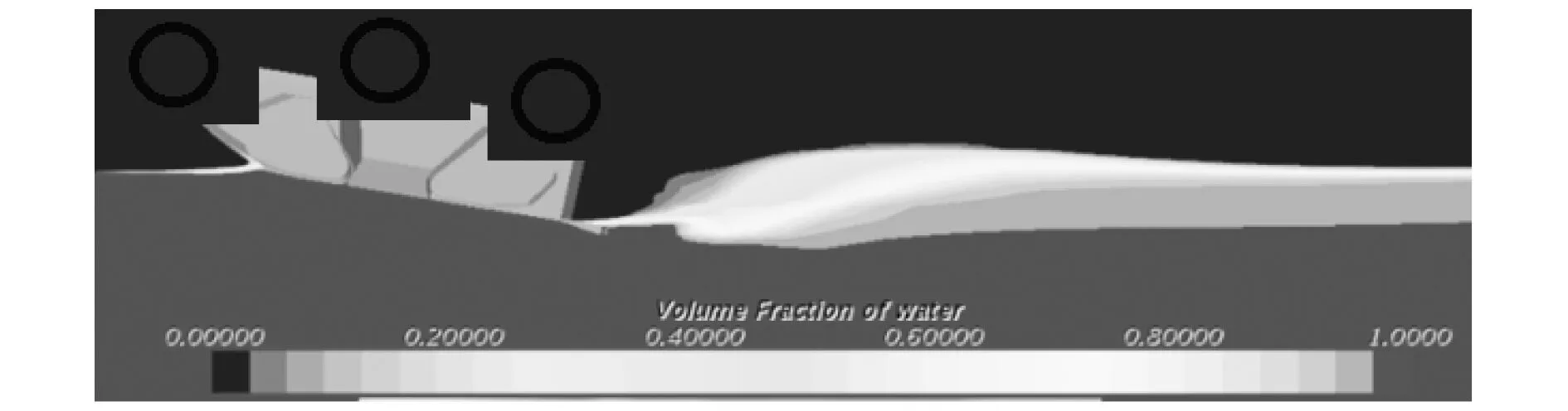
图2 实车对称面Fig.2 Symmetry plane of all scale car

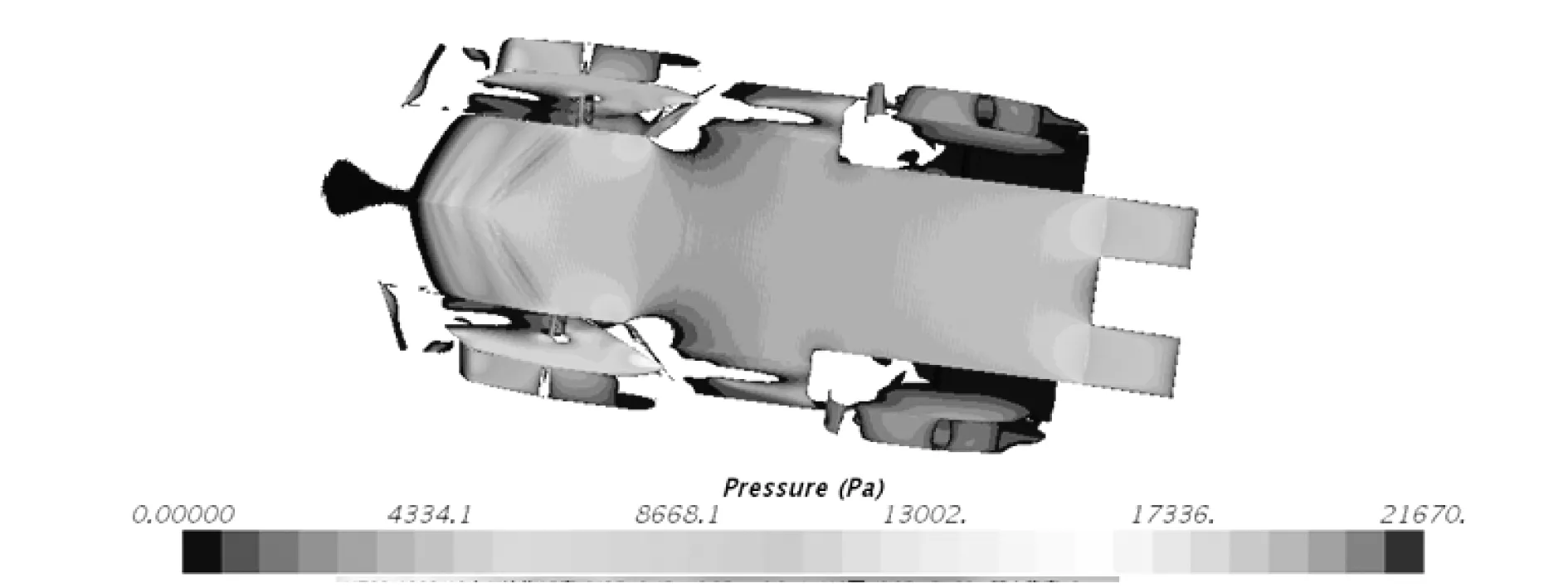
图3 实车正压Fig.3 Positive pressure of all scale car

2 模型试验

2.1 试验主要设备及模型安装

模型在605所拖曳试验水池进行试验,试验水池及拖车等水动力试验设备技术指标如下所示:

(1)水池主尺度。池长510 m,池宽6.5 m,池深6.8 m,水深5.0 m。

(2)拖车性能。速度范围0.1～22.0 m·s-1,车速稳定精度优于0.2%。

(3)测试手段。试验数据采集和处理分析自动化。

进行模型试验时,水池宽度不会引起阻塞效应。如图4所示,模型试验过程中,低速时模型首部上浪严重,因此在首部添加了挡板。

2.2 试验结果及分析

为验证仿真结果,对仿真计算的水陆两栖车辆模型进行了水动力性能试验。表3为两栖车辆模型的试验结果。

图4 模型试验Fig.4 Model test

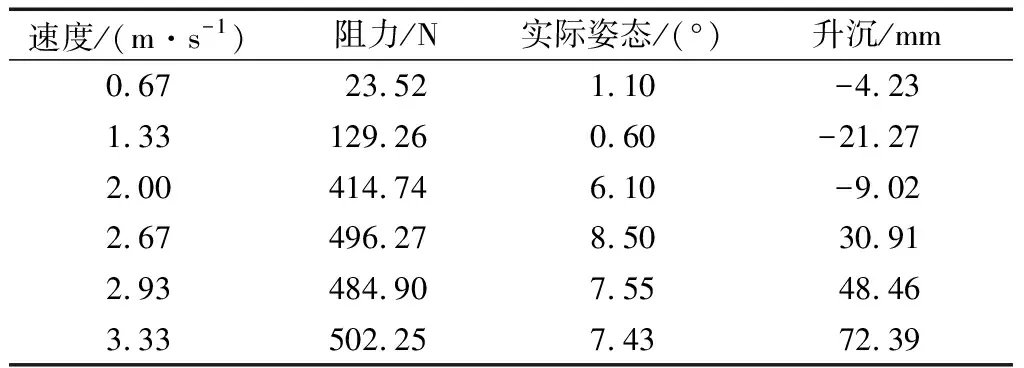
表3 模型试验值Tab.3 Experiment results of model

图5～6给出了车辆模型的水动力性能试验结果与速度的变化关系。随着速度增加,先埋首,后抬头,阻力值逐渐增加,2.67 m·s-1左右阻力趋向于一个峰值,这与船舶的运动现象类似。

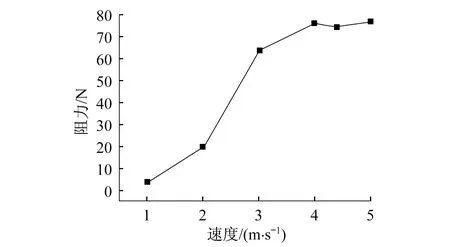
图5 阻力变化曲线Fig.5 Curve of drag with time

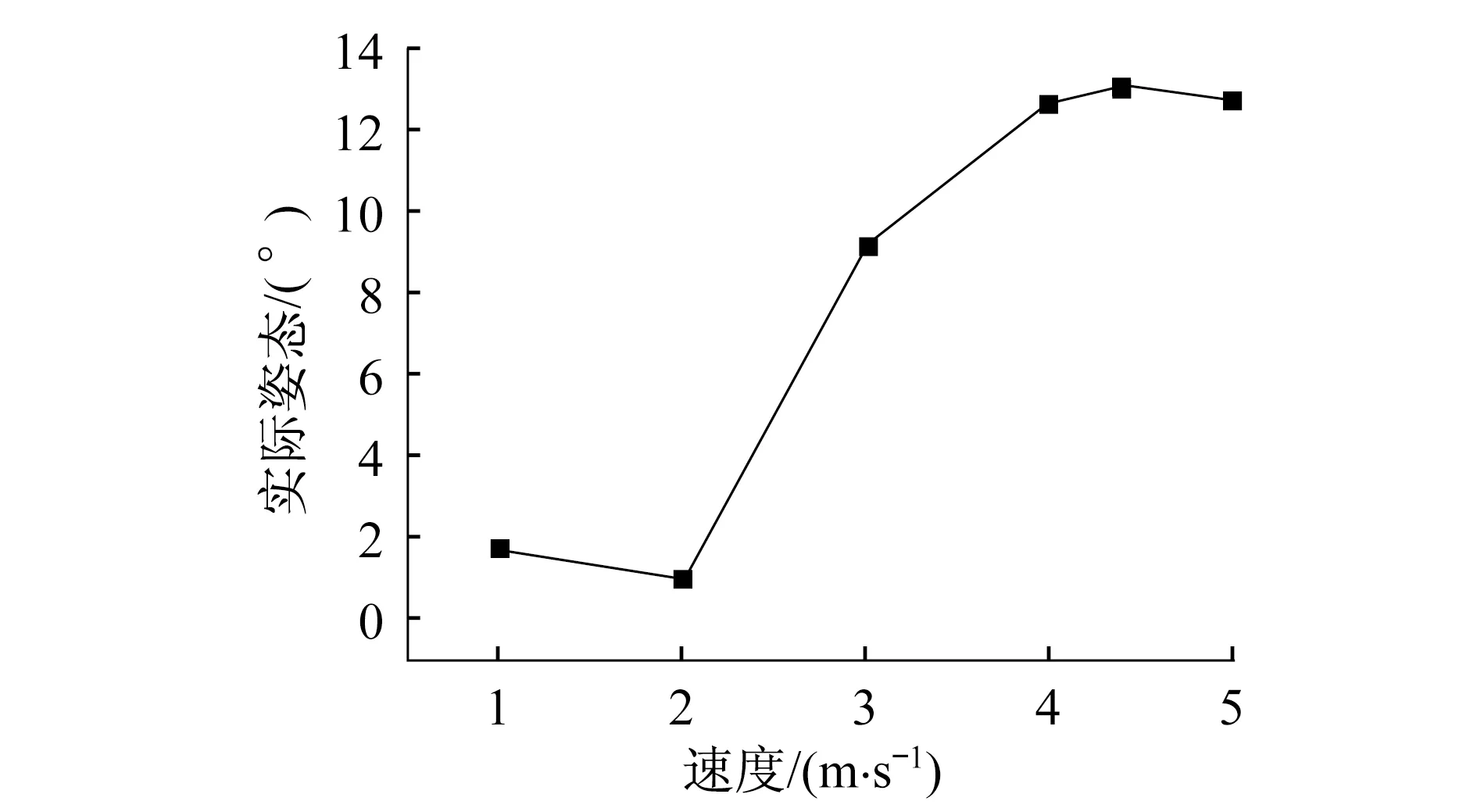
图6 实际姿态变化曲线Fig.6 Curve of heave with time

图7为两栖车辆模型试验的高速流场。从图7可以看出,由于车首为钝形,因此水线进水角较大。在车体首部还有大量的被车体掀起后很快就破碎的波浪,这种波浪称为破波。尾部呈现一波谷,此现象具有与船舶类似的特点,同时由于前车轮两侧压强较高,在该处形成较大的波峰。

3 仿真与试验对比分析

表4给出了速度为2.93 m·s-1时模型的仿真值与试验值,虽然两者存在一定的误差,但是该精度在进行两栖车辆选型及水动力性能仿真分析时也在可接受的范围内。结果表明:采用重叠网格可以较为准确地预报两栖车辆的水动力性能及求解三维流固耦合问题,运用数值方法分析两栖车辆的水动力特性是两栖车辆有效的研究方法。

图7 高速流场Fig.7 Flow field of high speed

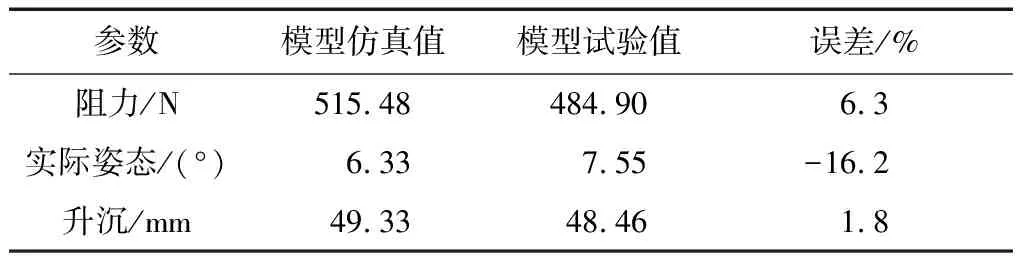
表4 模型仿真值及模型试验值Tab.4 Numerical and experimental results of model

表5给出了实车仿真值与模型试验值以及按比例换算得到的模型仿真值与模型试验值之间的关系。表5中按船舶换算比例得到的模型仿真值与试验值之间虽然存在一定的误差,但是也进一步验证了水陆两栖车辆的实车与模型之间的水动力性能换算在一定程度上可以采用船舶的弗劳德数相似的换算方法。综合比较表4与表5,可以得出试验值与仿真值在模型尺寸一致时,仿真值的精度更高。

图8～9显示了速度为2.93 m·s-1时两栖车辆模型周围的仿真与试验流场,仿真与试验结果在车体周围波形分布情况基本相同。仿真过程很好地捕捉了车体尾部的兴波,数值黏性的影响会使远车体的兴波有所衰减。鉴于此现象在车体尾部的开尔文区域进行网格加密。

表5实车仿真值及模型试验值
Tab.5Numericalresultsofallscalecarandexperimentalresultsofmodel

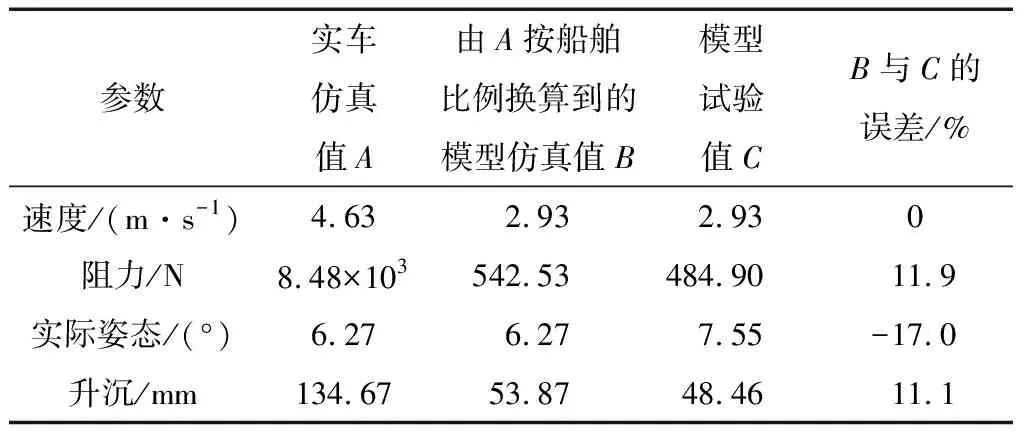
参数实车仿真值A由A按船舶比例换算到的模型仿真值B模型试验值CB与C的误差/%速度/(m·s-1)4.632.932.930阻力/N8.48×103542.53484.9011.9实际姿态/(°)6.276.277.55-17.0升沉/mm134.6753.8748.4611.1

图8 模型仿真流场(2.93 m·s-1)Fig.8 Numerical flow field of model(2.93 m·s-1)

图9 模型试验流场(2.93 m·s-1)Fig.9 Test flow field of model(2.93 m·s-1)

4 结论

本文基于计算流体动力学理论对自由液面的两栖车辆黏性绕流场进行了数值模拟并对数值结果进行了试验验证,得到以下结论:

(1) 采用重叠网格可以有效地完成水陆两栖车辆水上滑行的仿真工作,验证了重叠网格及流体体积法对求解三维流固耦合问题的有效性。

(2) 本文计算方法可以用来预测两栖车辆水面滑行状态下的水动力性能,并且指导试验方向,减少试验的盲目性和随机性,为水陆两栖车辆减阻及其设计优化提供一定的技术支持。

(3) 从模型试验值、模型仿真值及实车仿真值三者之间的关系,可以进一步验证水陆两栖车辆模型与实车水动力性能换算在一定程度上可以采用船舶的弗劳德数相似的换算方法。