基于交叉耦合控制的双轴轮廓加工系统设计研究

2018-09-20张耿汪有为

电气自动化 2018年4期

张耿, 汪有为

(1.合肥工业大学机械工程学院，安徽合肥 230009；2.奇瑞汽车股份有限公司，安徽芜湖 241000)

0 引言

在一般多轴机床系统中，每个轴是被单独的伺服控制回路设计成最小化轴向位置误差。即使用最佳设计的伺服算法，这些类型的传统解耦控制策略也不能够控制机床拥有足够的精度来满足新设计零件不断增长的精度要求。

双轴轮廓加工系统的电机按给定的信号运转，要求运动的实际轮廓与预期轮廓之间的轮廓误差控制在相对小的范围内，以提高数控加工的精度。为了实现这个功能，本文选择将单轴PID控制和交叉耦合策略同时应用到双轴控制系统中，以减小直线路径和圆弧路径下轮廓误差[1]。

1 双轴轮廓加工系统总体设计

双轴轮廓加工系统硬件组成包括上位机、DSP控制板、伺服电机驱动器和三相交流电机。如图1所示，上位机软件可以向DSP控制板发送预期的轮廓信号，并接收来自下位机的预期位置信息以及实际位置信息。DSP控制板通过伺服驱动器向电机发送控制信号并能接收电机的位置反馈。

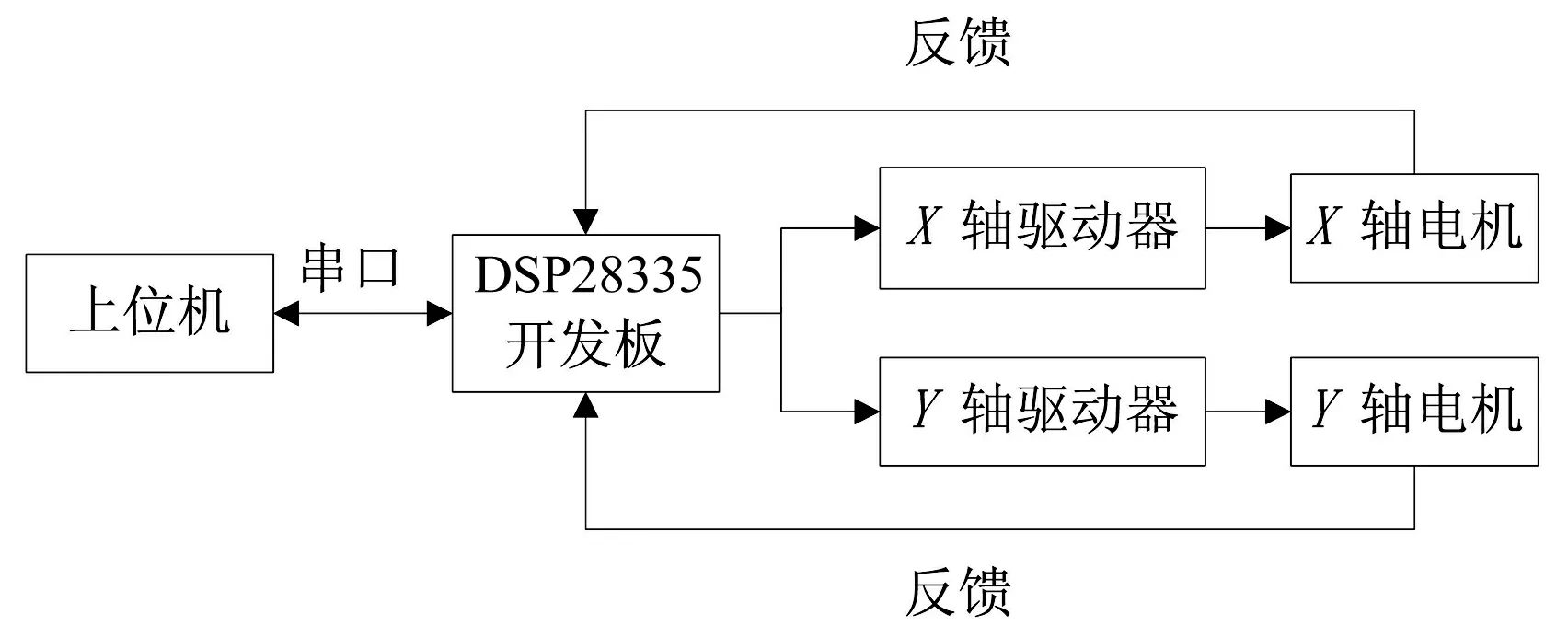
图1 硬件结构图

图2为软件设计结构图[2]，包含了1个插补单元、2个单轴控制单元、1个交叉耦合的系统控制器以及2个被控对象。就本系统而言， 2个被控对象就是2台三相交流伺服电机。

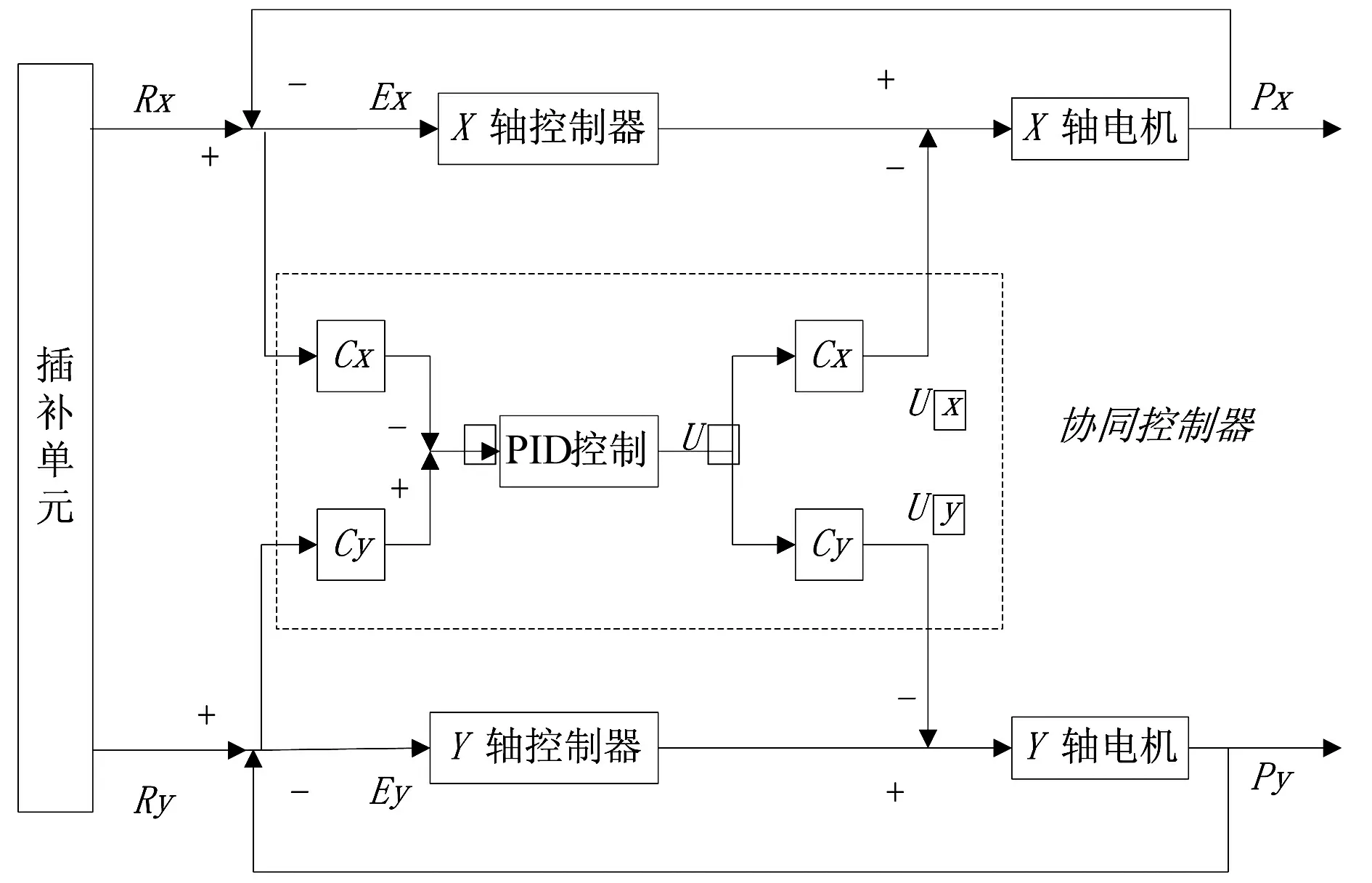
图2 软件结构图

插补单元就是一个直线路径或者圆弧路径的插补器，根据加工指令的进给速度，逼近预期轮廓。

单轴控制器在本系统中是一个PID控制器，它所产生的作用是为了减小每个轴的轴向跟踪误差。

交叉耦合控制器是针对双轴之间动态影响形成的轮廓误差精度问题，在直线路径或者圆弧路径下改善轮廓误差。

2 插补算法

插补计算的主要目标是算出下一插补点的坐标，即每个坐标的进给量ΔX和ΔY，根据加工指令的进给速度，以插补周期为时间单位，计算每一插补周期的轮廓步长，到达下一插补点。在进给过程中，对实际位置采样，与理论坐标值比较，在后一插补周期修正位置误差[3]。在本设计中，插补单元是一个直线路径或者圆弧路径的插补器。根据上位机发送到下位机DSP的位置信号，逐步逼近预期的轮廓。

无论进行直线还是圆弧插补，都必须要计算出单位时间的进给量，然后进行插补点的计算。

(1)

式中：V为指令进给速度， mm/min；T为插补周期， ms；L为单位时间进给量，μm/ms。

2.1 直线插补

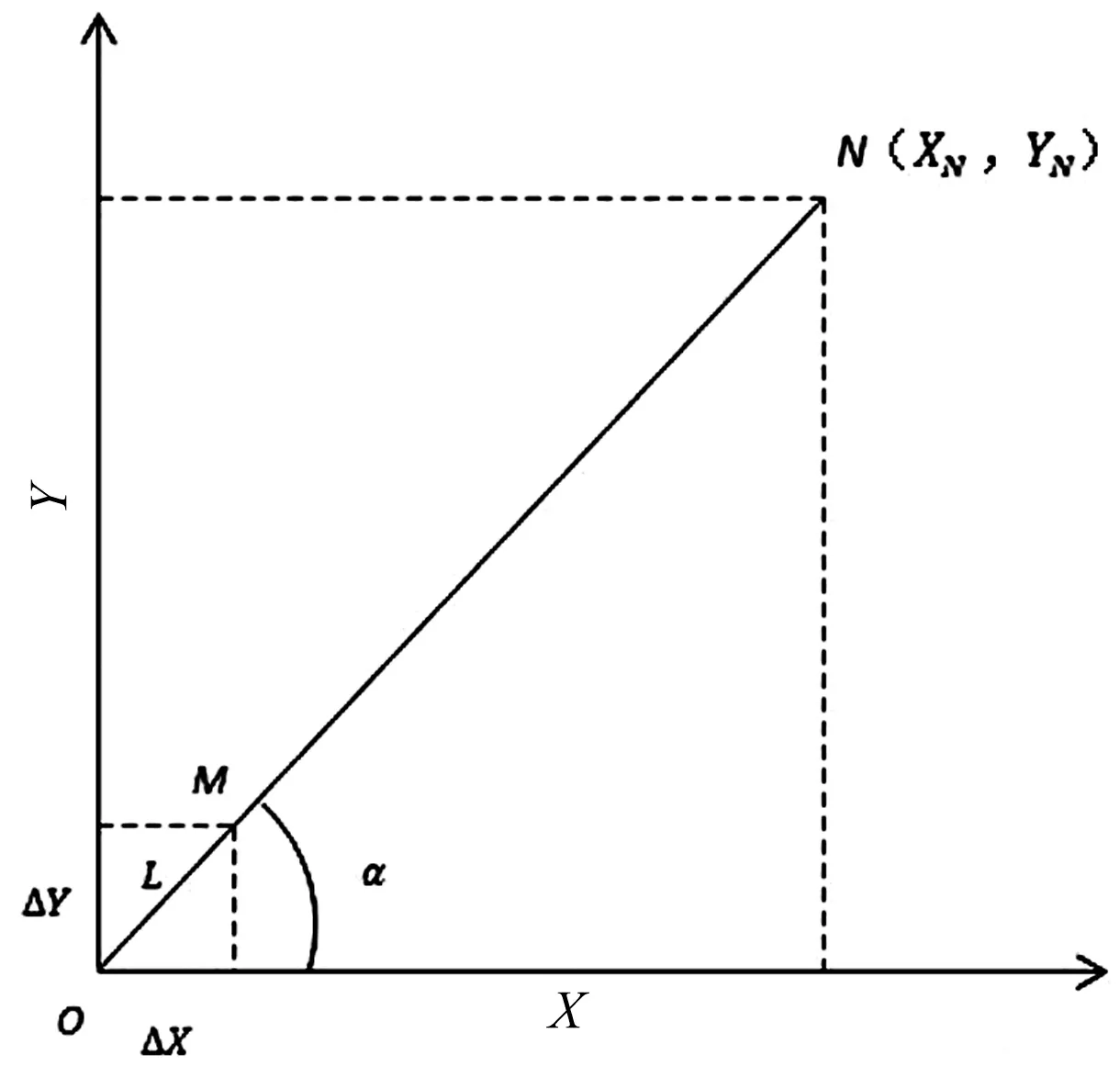
图3 直线插补模型

如图3所示，直线起点在O(0,0)，终点在N(XN,YN)，M为直线上一点，直线与X轴正方向夹角为α，单位时间进给量为L[4]。可得：

(2)

则X、Y轴坐标的进给量为：

ΔX=L×cosα

(4)

(5)

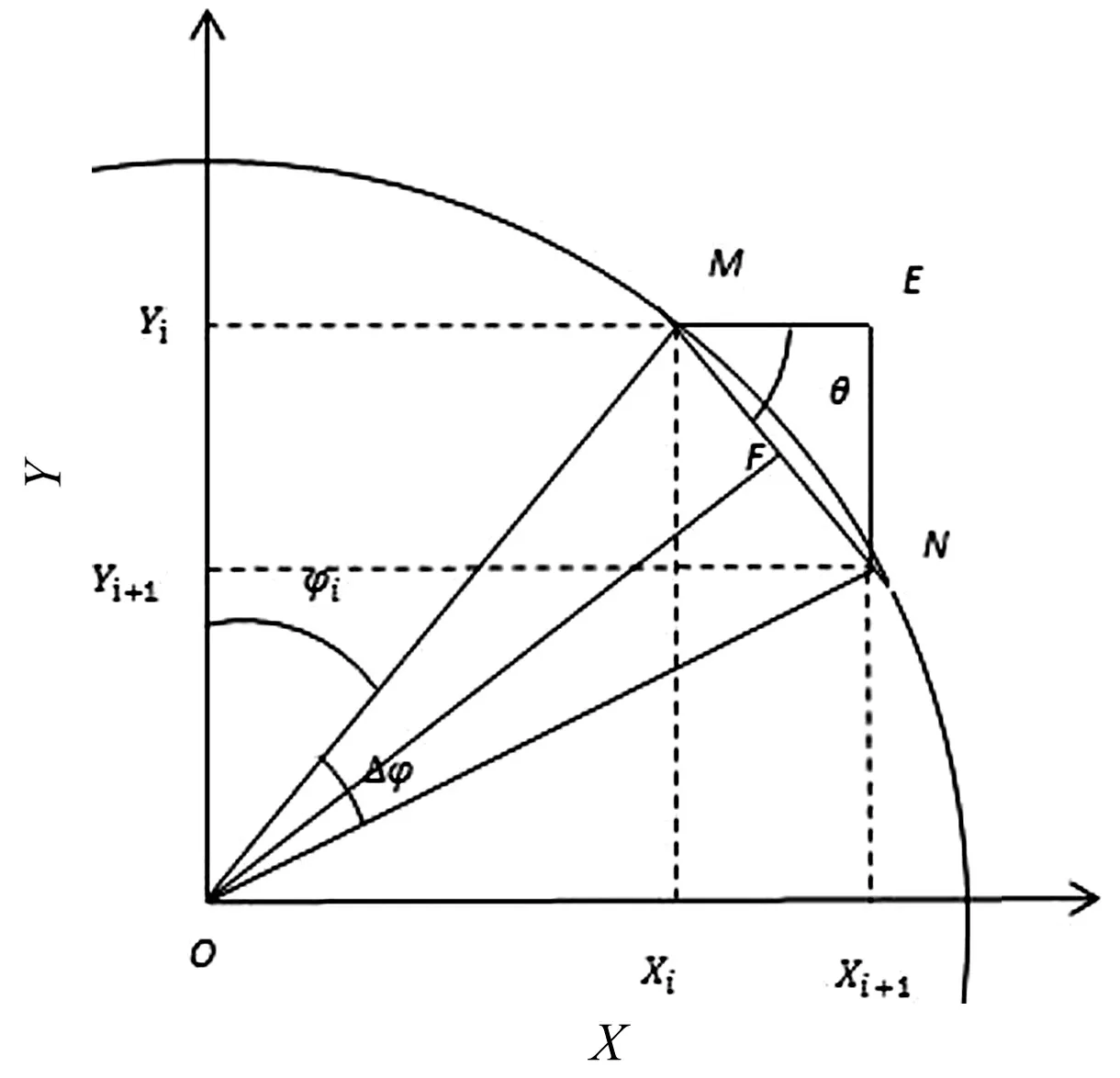
图4 圆弧插补模型

2.2 圆弧插补

圆弧插补，就是以步长为相邻两个插补点间的弦长，由半径和当前插补点的坐标，计算当前插补点到后一插补点的进给量△X和△Y[5]，如图4所示。可得：

∠MOF=∠NOF=0.5Δφ

(6)

θ=φi+0.5Δφ

(7)

(8)

则X、Y轴坐标的进给量为：

(9)

(10)

3 单轴PID控制

双轴伺服控制系统是要控制两个轴协调运动，对单轴的运动的精确控制是实现对双轴运动控制的重要前提。为提高X轴或Y轴的单轴跟踪误差，需要将单轴的PID控制器加到单轴控制中，对轮廓加工过程中的误差进行补偿[6]。

3.1 PID原理

被控对象通过PID控制器求出系统的偏差，然后对偏差进行比例、积分和微分的线性组合，获得偏差e(t)的过去、现在以及未来的相关信息[7]。数字式的PID增量形式为：

u(k)=u(k-1)+c0×e(k)+c1×e(k)+
c2×e(k-2)

(11)

其中：c0=Kp×(1+T/Ti+Td/T)

c1=-Kp×(1+2×Td/T)

c2=Kp×Td/T

式中：u(k) 为当前单轴的控制量；u(k-1)为上一次单轴的控制量；e(k) 为现在的偏差值；e(k-1)为上一次的偏差值；T为采样周期；Kp为比例系数；Ti为积分系数；Td为微分系数。

3.2 PID调节

PID控制器中参数取值的方法杂多，实际调试中普遍采用试凑法[8]。通过试验确定第一轴的PI参数Kp=1.4、Ti=0.2，第二轴的PI参数Kp=1.1、Ti=0.175。

单轴系统的软件流程图设计如图5所示，通过插补计算，计算偏差和PID控制调节，得出下一插补点的位置，控制电机的角度与方向。

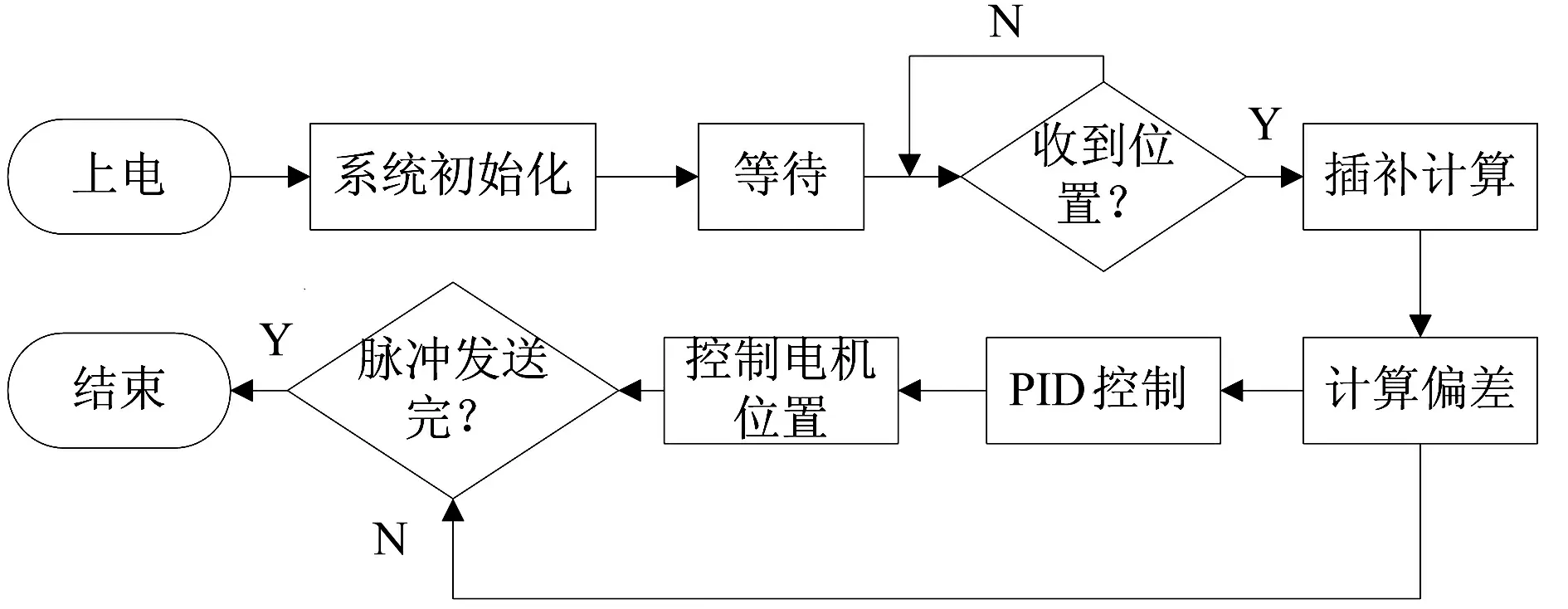
图5 单轴PID功能程序流程图

图6为PID调节前后的脉冲偏差对比图。可以看出，PID调节前，偏差Ek在+9～+14个脉冲之间，PID调节后，偏差Ek在-3～+3个脉冲之间。所以，单轴PID能够明显减小系统的轮廓误差。

图6 PID调节前后的脉冲偏差对比图

4 交叉耦合控制

图2中虚线部分是交叉耦合部分的原理示意图，它的输入是两个单轴的跟踪误差，输出是轮廓误差值进行PID计算后的控制量，再将该控制量按一定比例分配到两个单轴控制[9]。下面分别以直线路径和圆弧路径分别对双轴交叉耦合控制系统的轮廓误差进行分析。

4.1 直线运动的轮廓误差模型

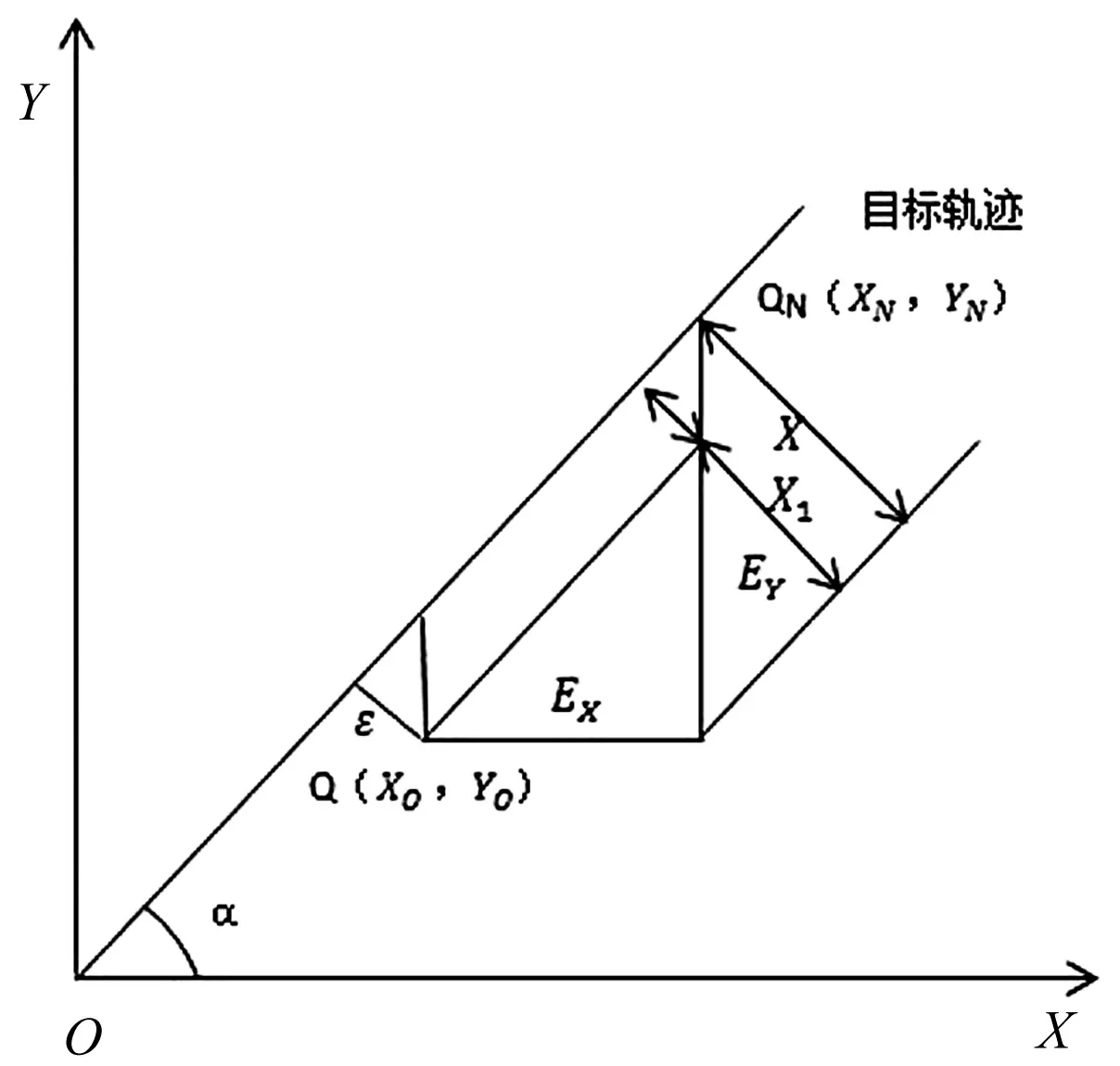
图7 直线运动的轮廓误差示意图

对于直线路径下的轮廓误差建模如图7所示。图7中QN(XN,YN)为任意时刻预期点，Q(XO,YO)为同一时刻实际所运行到的点，α为参考输入位置处轨迹切线与同X轴正方向的夹角，E为跟踪误差，ε为轮廓误差，E沿X、Y轴分解得到EX、EY[10]。

由图7可得：

(12)

则：

ε=-EXsinα+EYcosα

(13)

由式子可得E沿X轴与Y轴的值与ε之间的函数关系，观察上式可知当路径为直线运动时，ε为EX与EY的线性表达式。只要运动路径不发生变动，斜率保持固定，并不需要变增益交叉耦合理论，只用在两轴方向分别加一个固定的补偿量即可。

4.2 圆弧运动的轮廓误差模型

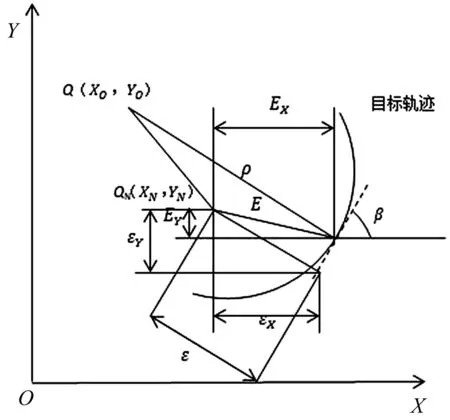
图8 圆弧运动的轮廓误差示意图

对于圆弧路径，曲率半径ρ即为圆的半径，在所取点附近用圆来代替曲线，当线段取得很小时这样的操作是可行的。图8为圆弧路径下所构造的模型。QN(XN,YN)点是运行时实际点的位置，Q(XO,YO)为这一时刻预期曲线弧线对应预期点处的曲率圆心坐标。

系统轮廓误差可表示为：

(14)

经过泰勒展开后得到：

ε=-(sinβ-EX/2ρ)×EX+(cosβ+EY/2ρ)×EY

(15)

在系统运行时，β的值在不断地变化，下位机需要根据系统的位置不断地计算出交叉耦合算法的增益。

4.3 交叉耦合控制的软件设计

交叉耦合控制器的输入是两个轴的跟踪误差EX和EY，经过交叉耦合后，输出分别被加到两个轴。

如图9所示，当系统的EX与EY都产生后，交叉耦合算法会先判断它所对应的轮廓误差模型，以求得轮廓误差值，然后对轮廓误差值进行PID计算，最后将求得的控制量分配到X、Y轴上，使得轮廓误差的值被优化，精度有所提高。经整定得到Kp=0.55、Ti=1.3、Td=0.000 5。

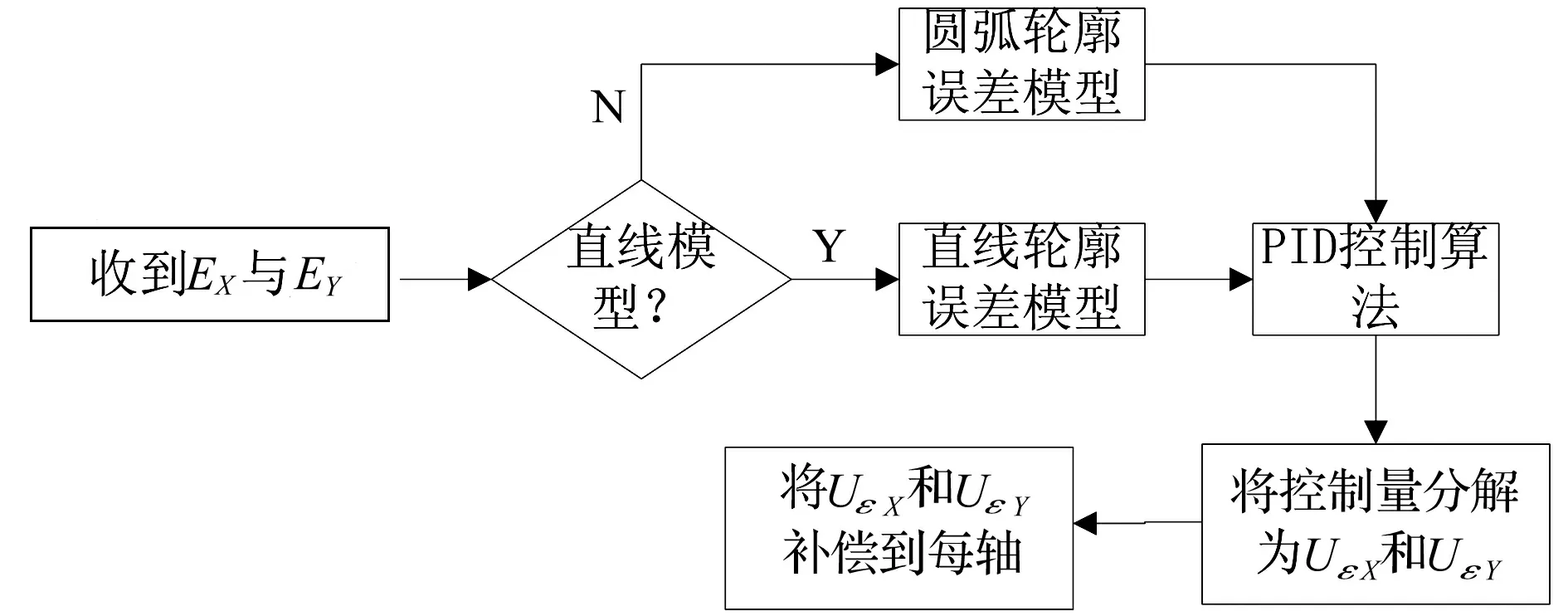
图9 交叉耦合程序流程图

5 试验

为了验证所设计的交叉耦合控制策略能否减小系统的轮廓误差，需要在带负载条件下，对没有添加交叉耦合控制策略的轮廓误差值与添加交叉耦合控制策略的轮廓误差值进行比较。试验选择的伺服电机额定电压36 V、功率0.2 kW，所带的负载为600 g的砝码。

5.1 直线误差分析

5.1.1不带交叉耦合控制策略的直线误差分析

当不带交叉耦合控制策略，系统控制双轴走直线时，根据直线插补原理可知，此过程相当于双轴各自的PID控制进行匀速运动。电机没有正反转换向的情况发生，运动比较平缓。轮廓误差值如图10所示。

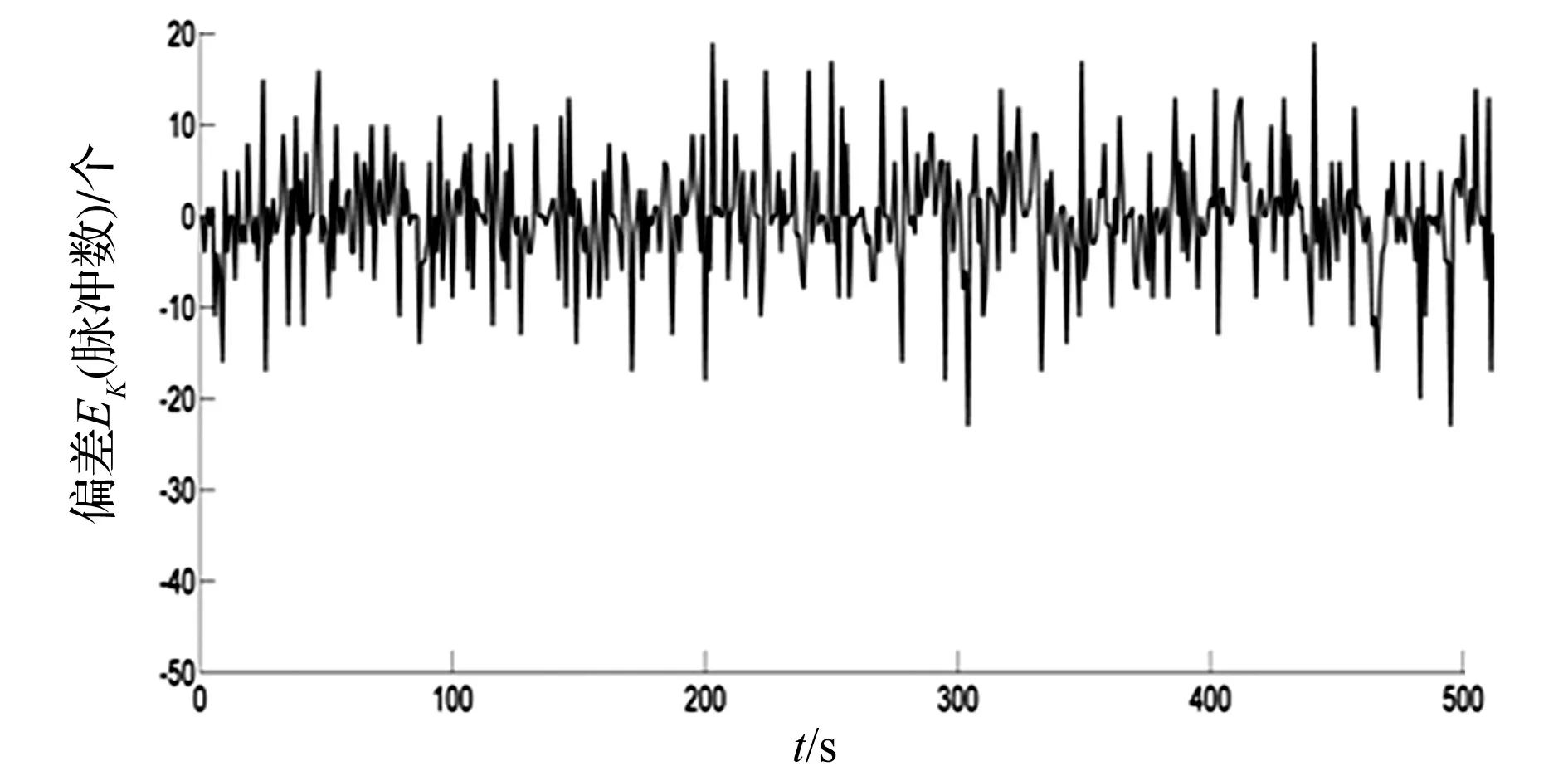
图10 不带交叉耦合的直线轮廓误差折线图

由图10可以看出，系统的轮廓误差在-26～+26个脉冲之间，大部分集中在-1、0、+1，三者约占40%左右，超过5个脉冲的约占20%。

5.1.2带交叉耦合控制策略的直线误差分析

带交叉耦合控制是双轴PID控制的优化，交叉耦合控制能够结合X轴的跟踪误差与Y轴的跟踪误差来控制轮廓误差值，使实际轮廓更接近预期的轮廓。轮廓误差值如图11所示。

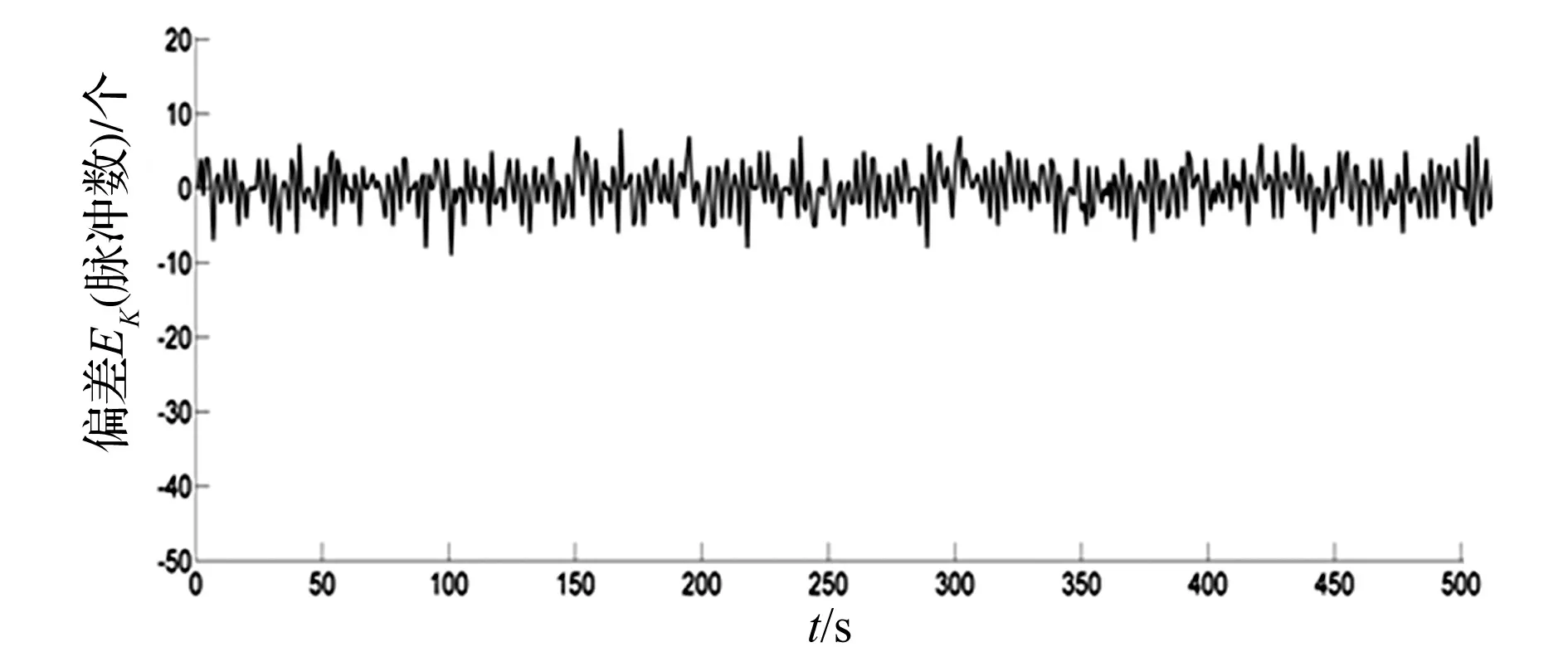
图11 带交叉耦合的直线轮廓误差折线图

由图11可以得到，轮廓误差值最大不超过4个脉冲，最小不超过6个脉冲，轮廓误差值超过5个脉冲的比例几乎等于零。与图10所示的轮廓误差值相比，性能有了明显的提高，不仅轮廓误差的最大值变小很多，也更加集中于0附近，使系统误差更加稳定、精度更高。

5.2 圆弧误差分析

5.2.1不带交叉耦合控制策略的圆弧误差分析

当不带交叉耦合控制策略、系统控制双轴走圆弧轮廓时，根据圆形轮廓插补原理可知：当系统运行到与X轴或Y轴垂直时会使相对应的轴发生方向上的改变。并且在走顺时钟圆形轮廓时，当系统运行在第一和第三象限时，X轴的插补脉冲数会减小，Y轴的插补脉冲数会逐渐增多；当系统运行在第二和第四象限时，X轴的插补脉冲数会增多，Y轴的插补脉冲数会逐渐减少。轮廓误差值如图12所示。

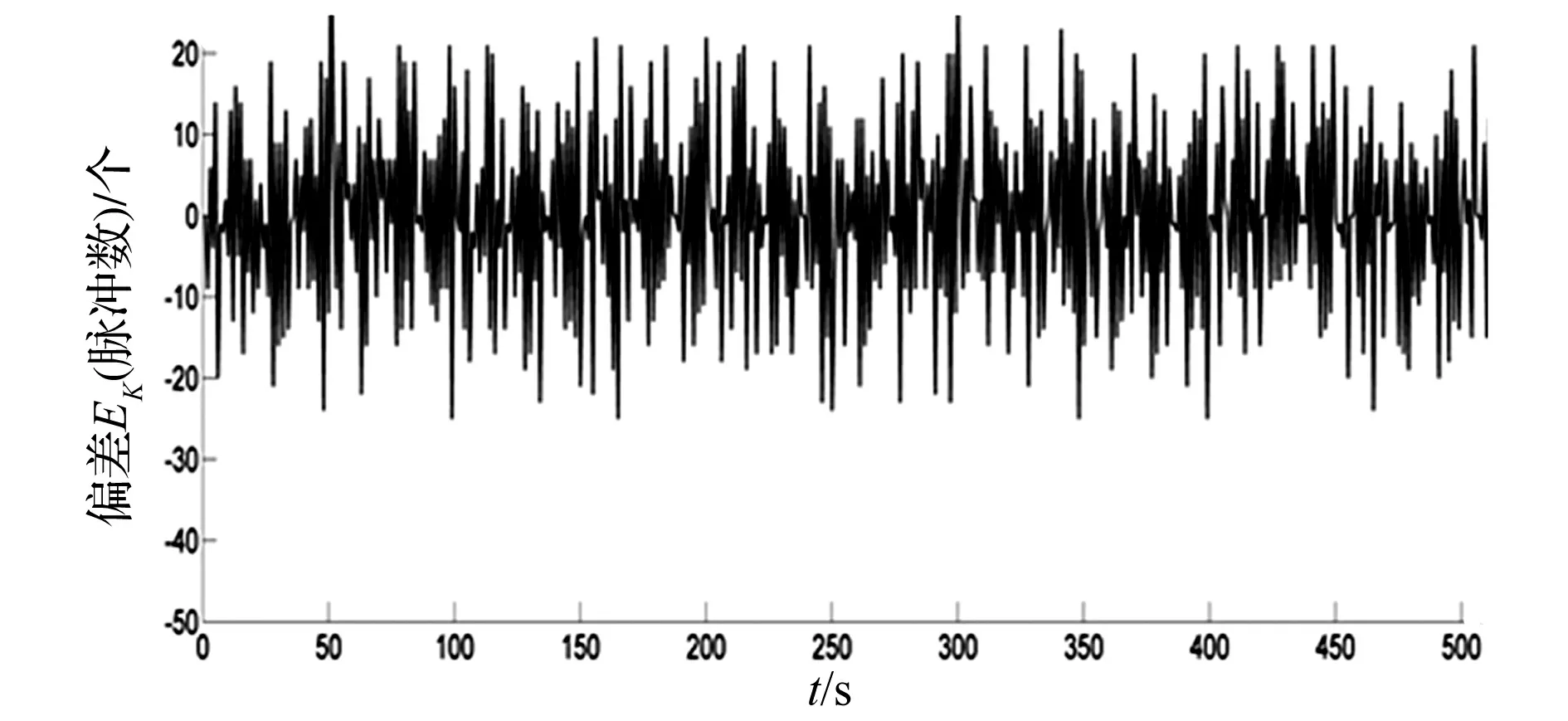
图12 不带交叉耦合的圆弧轮廓误差折线图

由图12可以得到轮廓误差值最大不超过22个脉冲，最小不超过-29个脉冲，集中在0个脉冲值附近，但是误差值超过5个脉冲的比例上升为26%附近。

5.2.2带交叉耦合控制策略的圆弧误差分析

带交叉耦合的圆弧路径与带交叉耦合的直线路径有所不同，因为在直线路径下，走直线的斜率是一定的，参数很精确，并且不需要时刻改变系统运行时候的参数。但是在走圆弧时候，由于不同时刻所在圆的位置的不同，造成所走轮廓上切线斜率不一样，因参数与斜率成一定的函数关系，所以在走圆弧路径时候，需要每次走完一组脉冲后改变系统的参数值。轮廓误差值如图13所示。