四面体网格剖分下速度与反射界面的同时反演

何雷宇 严 星 白超英*③

(①长安大学地质工程与测绘学院地球物理系，陕西西安 710054； ②新疆财经大学网络与实验教学中心，新疆乌鲁木齐 830011； ③长安大学计算地球物理研究所，陕西西安 710054)

1 引言

层析成像始于医学中的CT技术，Aki等[1]首次将其应用于地震学研究中。经过四十多年的发展和完善，地震层析成像已成为研究地下地质结构行之有效的主要技术途径之一，并且涌现出多种成像的方法技术[2]。

传统射线类走时成像方法一般采用规则网格单元(2D中的矩形网格单元、3D中的立方体网格单元)模型参数化方式，这种简单模型参数化可以很容易地通过网格节点的编号确定该节点的空间坐标，从而节约计算机内存空间。然而这种简单的模型参数化形式也存在诸多问题。例如：若要对复杂区域进行较为精确的描述，则必须进行网格单元的精细剖分，从而增加计算时间。更为重要的是规则网格单元参数化对起伏地表及地下不规则波阻抗界面无法进行准确的拟合，从而造成正演中不必要的计算误差，进而导致反演中出现假象。

另一方面，从反演角度来说，规则网格的精细剖分，意味着更多的未知模型参数参与反演，从理论上就需要更多的射线进行覆盖，故而求解的方程组的维数也将大大增加，数据对模型的约束也就越差。此外，更多的未知参数意味着参数矢量中欠定的和位于零空间的分量数目更多，性态大大变坏； 层析反演难度的增加，通常需加入正则化约束以改变方程组的病态，而这又增加了存储量和计算量[3]。

上述问题的有效解决方案之一是采用不规则网格单元(包括三角网格或四面体网格)进行模型参数化。例如可根据模型中不同区域物性的复杂程度选择不规则网格单元的大小，同时不规则网格单元剖分对起伏地表和地下波阻抗界面(含不规则异常体)的描述更加精确，从而确保了正演所需的计算精度。反演中由于未知模型参数相对较少，则所需射线也相对较少，故而待求解的方程组维数也大大减小，从总体上减少了反演的存储量[3]。

三维情况下使用四面体网格单元的另一个优势在于：实际中地震台站的分布是不均匀的，如北京圈附近的台站密度与我国西部地区的台站密度、陆地的台站密度与海洋区域的台站密度是不同的，加之天然地震的发生本身就具有不均匀性，两者结合造成了地震数据覆盖密度的极度差异性，所以有必要对数据密度大的区域进行更细致的剖分以增加数据的利用效率。

不规则网格单元在地震数值模拟中有较为广泛的应用。正演方面，如在波场模拟中使用的不规则网格[4，5]、变网格[6]和贴体网格[7]等。而在地震射线追踪研究方面，李波涛等[8]将三角剖分与波前重建法相结合，实现了初至波射线路径和走时的快速计算； Yu等[9]引入单元密度控制函数，实现了三角网格下初至波射线追踪的全局算法； Lan等[10]借助于流体力学中的贴体网格和坐标变换，引入Lax-Friedrichs快速扫描法求解与地形有关的程函方程以获取地震波初至走时场。

上述几位学者的研究主要是解决了2D模型中不规则网格单元模型参数化下初至波走时的计算与射线追踪问题。Vinje等[11]在开放模型的波前构造法中将三角网格应用于反射界面的描述和波前面的描述，并实现了反射波射线追踪。赵瑞等[12]将梯形网格与矩形网格结合，实现了多震相射线追踪； Bai等[13]提出一种基于三角(2D)或四面体(3D)单元剖分下的最短路径射线追踪算法(Triangular Shortest-path Method，TSPM)，并实现了多震相地震射线路径的追踪与走时计算； 李晓玲等[14]在赵瑞等[12]研究的基础上，将混合网格下的射线追踪算法推广至各向异性TI介质中。但混合网格仅可模拟起伏地表，无法对模型内部进行差异化剖分，优势有限； 随后，李兴旺等[15]实现了四面体网格参数化下TI介质中的多震相射线追踪。

基于不规则网格单元剖分下的层析成像研究最早可追溯到20世纪80年代。Tarantola等[16]意识到在地震层析成像中使用固定的均匀网格单元的一些局限性并提出了block-less模型参数化方法； Sambridge等[17]率先将Delaunay四面体和Voronoi多面体应用于地震层析成像领域； Gudmundsson等[18]利用Delaunay四面体和Voronoi多面体进行模型参数化，使用初至P波层析成像改进了区域上地幔地球参考模型； Curtis等[19]通过对给定的一组点采用Delaunay三角化来描述模型的速度结构，进而研究了2D情况下的井间反演问题； Böhm等[20]用Delaunay三角形和Voronoi多面体在3D反射层析成像中发展了一种自适应反演方法； Sambridge等[21]使用自适应Delaunay四面体网格单元进行了全球P波层析成像研究。

中国国内对不规则网格层析成像的研究较少。成谷等[3]对比了三角网格层析成像与矩形网格层析成像的优缺点； 于师建等[22]采用三角网格模型参数化进行走时层析成像研究。他们所做的研究主要是不规则网格参数化下初至波走时层析成像问题，但并未引进反射波。鉴于此，本文研究了2D三角网格模型参数化的多震相联合反演及速度与反射界面同时反演问题[23]。为了更好地解决实际地震工作的需要，还将该算法进一步推广至3D四面体网格。在此过程中，要解决的主要问题是如何进行模型参数化、用参数化后的网格进行射线追踪及如何求解Jacob矩阵元素并进行合理分配。显然，3D情况下算法实现的难度总体上大于2D情况。

文中基于Multistage TSPM正演算法[13]，结合共轭梯度求解带约束的阻尼最小二乘解反演算法，同时得到了四面体网格单元下走时关于速度、走时关于反射界面的偏导计算公式； 讨论并实现了四面体网格单元模型参数化下3D复杂模型中地震多震相走时同时反演成像技术。本文主要研究内容包括： ①反射界面已知时地震多震相走时联合成像技术； ②多震相走时联合同时反演速度模型和反射界面的技术。数值模拟实验结果表明，四面体网格单元模型参数化下的多波走时成像及同时反演成像结果较为可信，可作为起伏复杂介质中速度场和反射界面重建的一种有效方法。

2 多震相射线追踪算法

2.1 模型参数化

本文采用的网格由开源的Tetgen生成[24]。利用Multistage TSPM进行射线追踪之前，首先要对模型进行四面体网格单元参数化(图1)。采用四面体单元进行模型参数化时，定义四面体单元的四个角点为主节点。为了增加射线出射角的覆盖率(即保证正演的计算精度)，在四面体单元的四条边上等间距插入次级节点，四条边插值结束后再对四个面进行插值。四面体网格单元内部没有节点，但炮点和检波点可置于其中(图1)。模型中速度的采样是在主节点上进行，而次级节点上的速度则是通过速度插值得到(详见下文)。

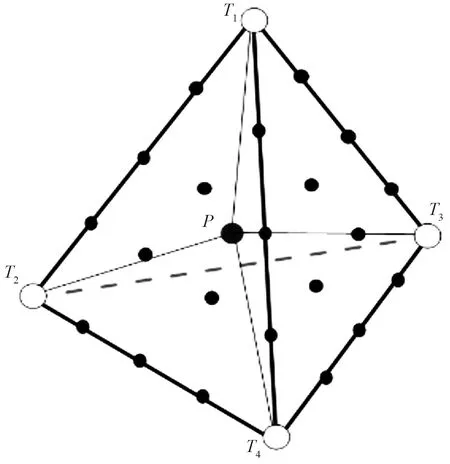
图1 速度插值示意图

2.2 最小走时的计算和速度插值

从炮点开始计算，节点走时的计算公式为(两点间距离除以平均速度)

(1)

式中：i是波前点中当前的次级震源；j为待计算任意节点；Nj为待计算节点的集合；ti为炮点到达i节点射线的最小走时；D(xi,xj)是节点i与j之间的距离；v(xi)、v(xj)分别是i和j节点上的速度。当i节点不是主节点时，可通过下式求取该节点速度

(2)

式中：vj表示所在单元各主节点的速度，在三维模型中k=4；uj为点在四面体中的体积坐标，例如图1中P点在四面体T1T2T3T4内的体积坐标uj可表示为

(3)

式中V(PT2T3T4)、V(T1T2T3T4)等表示各四面体的体积。显然，四点共面时体积为零。

2.3 分区多步计算原理

完成模型参数化和速度插值之后，为了减少计算量，避免对射线未经过区域的计算，可根据反射界面的起伏形态将模型分成若干(层状)区域。从震源所在区域开始计算，根据给定的震相种类对特定射线进行追踪并计算节点的最小走时。以图2模型为例，该模型共有上下两个界面，将整个模型分为3个区域，假设震源和台站均位于地表，现在需追踪第一个反射界面的反射转换波P1S1(数字1表示计算区域编号，上标代表上行波，下标代表下行波)。计算步骤为： ①选择第一区为计算区域，调用P波速度模型从震源开始计算直至一区所有网格全部计算完毕； ②保留一界面上的走时和射线路径，同时选择一区为计算区域，从界面一上搜索出走时最小点并将该点作为次级震源点，调用S波的速度模型，计算该区域的走时和射线路径。按照上述原理可实现多震相地震射线的追踪计算。

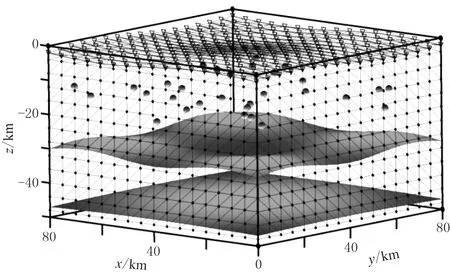
图2 模型示意图

3 反演算法

3.1 反演目标函数

在速度与反射界面同时反演中，走时对界面深度的偏导数远小于走时对速度的偏导数，导致同时反演中界面基本不会更新。因此本文采用不同参数归一化反演方法。多震相走时同时反演问题可归结为带约束的阻尼最小二乘最优化问题，其目标函数为

(4)

(μCm+ATCdA)Zmm=ATCdd

(5)

式中Cm、Cd为模型和数据空间的协方差矩阵。该式是对非线性问题局部线性化的基本反演公式，其解具有局域解的特征。为了得到具有实际物理意义的解，可采用Zm、Cm及Cd的先验信息。因此，选择不同组合的(Cm，Cd)可得到不同形式的反演解。若μ=0,Cd=I则式(5)变为经典的最小二乘问题；若Cd=Cm=I，Zm=W，A=GW，这里W是表征射线宽度的带宽矩阵，则式(5)变为Meyerholtz等[26]提出的卷积压制法。本文主要采用Tarantola等[27]提出的广义带约束的阻尼最小二乘反演解，即Cm、Cd分别为模型和数据空间的协方差矩阵的逆矩阵，其解为

(6)

该解的约束条件是

式(4)可用迭代的共轭梯度法进行求解[28，29]，其关键是如何求解四面体单元中具有偏导性质的Jacobi矩阵中的元素。

3.2 Jacobi矩阵的求解

根据射线理论可知，三维情况下沿某一射线路径Rj的走时tj可用下式表示

(7)

式中：vc(x,y,z)为四面体单元内速度函数； ds为射线的微分元； 模型参数化后，射线路径Rj上的走时可写成求和形式

(8)

式中：n为该射线所穿过的四面体单元总数；Rj,k表示穿过第k个四面体单元的射线长度；vc,k(x,y,z)表示该四面体单元的速度分布。

速度与界面同时反演时的Jacobi矩阵包括两部分：走时对速度变化的偏导数和走时对反射点深度变化的偏导数

(9)

式中：vk是第k个四面体单元的速度分布；tj是第j条射线的走时；zk是第k个反射点的深度值。

射线穿过某个四面体单元时，其走时对速度的一阶偏导可用通过该四面体单元射线两端点的平均值来代替[30]

(10)

其中

式中：ki和kj是穿过第k个四面体单元内射线的两个端点；vb(k)是第k个四面体单元内四个主节点的速度值。

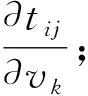
(11)

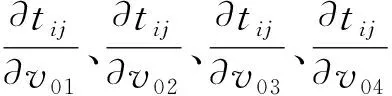
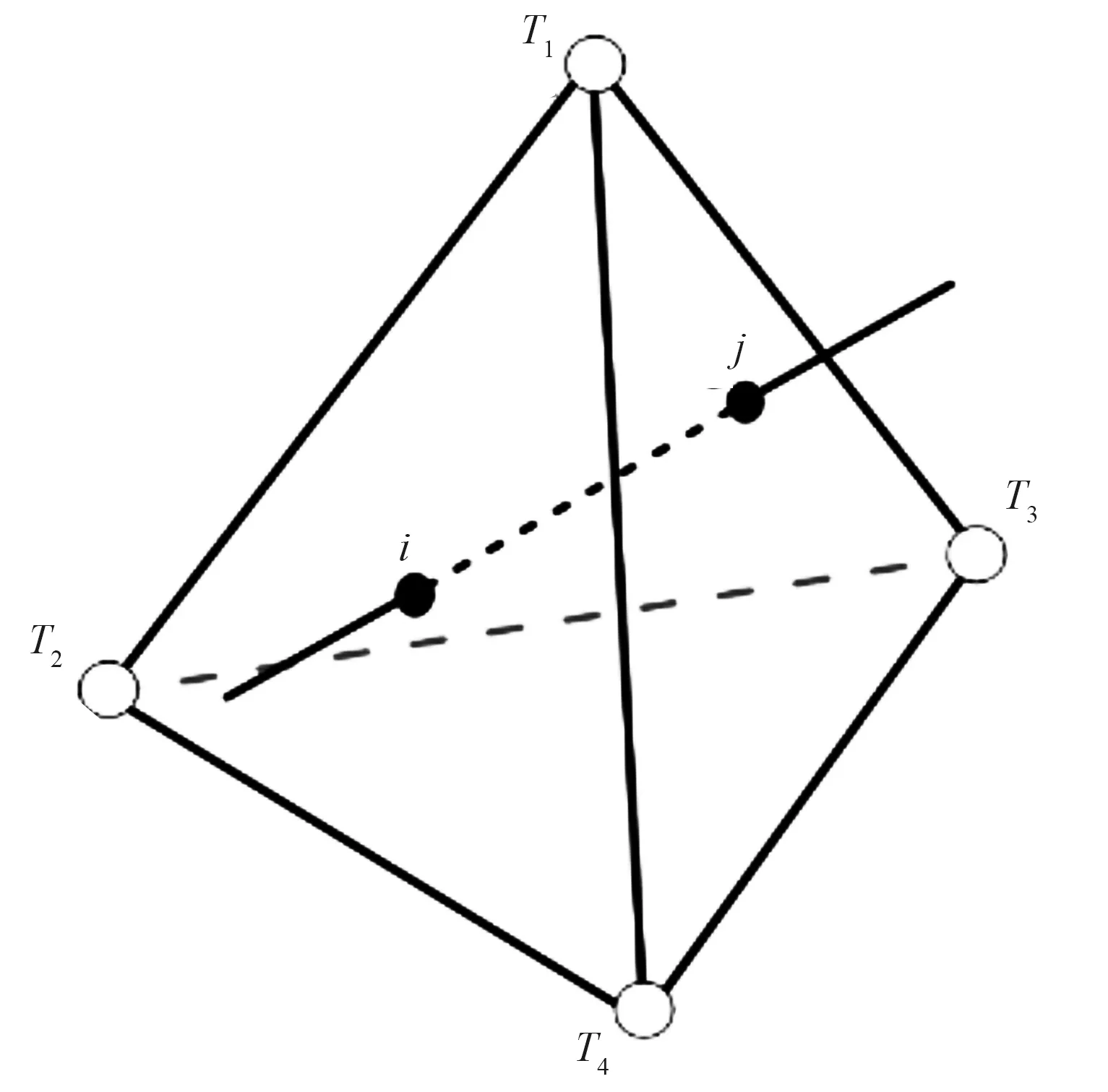
图3 穿过某一个四面体网格的射线示意图

式(10)中，界面p点处走时关于界面深度的导数为[20]

(12)

式中：γ1为入射向量与界面法向量的夹角；γ2为出射向量与界面法向量的夹角；v1,v2分别为入射向量侧和出射向量侧的速度。实际计算时，只需记录入射点，反射点和出射点便可得到入射向量和出射向量，再求取在反射界面上反射点处的法向量即可得到走时对界面深度的偏导。

本文采用式(11)计算走时对速度的偏导，用式(12)计算走时对界面深度的偏导。在速度与界面的同时反演中，为了避免因反射界面更新引起某些区域的过度(或欠)更新，笔者对两种不同类型的Jacobi矩阵元素进行了归一化处理。

4 数值模拟分析

4.1 计算效率分析

已知反演的耗时中正演的占比超过90%，所以同时反演的计算效率主要取决于选用的射线追踪方法。为此对比了立方体模型参数化和四面体模型参数化下单炮正演的CPU计算时间，所选立方体模型的尺寸为80km×80km×48km。将主节点间距固定为8.0km，将次级节点间距从4.0km到0.25km逐步减半缩小，并记录不同模型参数化下的计算时间(所用计算机：Dell，Intel(R) Core(TM)2 Duo CPU E7200，主频2.52GHz)。

一般来说，无论采用何种模型参数化方式，当主节点的间距固定时，其正演的计算效率主要取决于次级节点的间距，但是随着次级节点间距的减小，两种模型参数化下的CPU时间差将大幅减小(表1，CPU时间差从次级节点间距为4.0km时的近200倍降到了次级节点间距为0.25km时的不到2倍)。从总节点数和CPU时间的关系图(图4)中也可得出类似结论。两种模型参数化下的CPU时间都与次级节点间距成近似指数型的关系，但是立方体模型曲线的斜率更大。随着总节点数目的增加，两条曲线最后完全发散。

从图4和表1可见，在需要高精度计算的情况(即更多的次级节点)下，上述两种模型参数化的计算效率处于同一水平。由于CPU时间中90%以上都被正演所消耗，因此这个结论也同样适用于后面的同时反演部分。

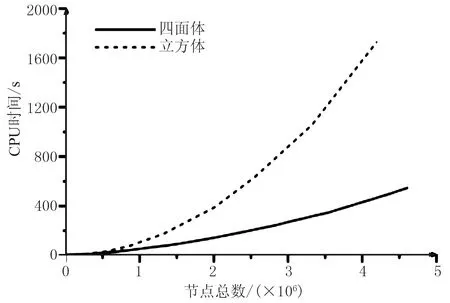
图4 CPU时间随节点总数的变化关系曲线

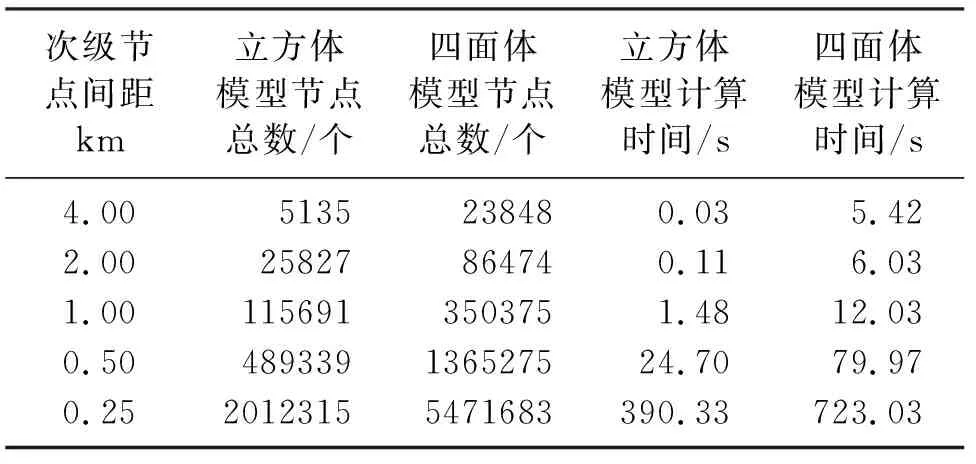
次级节点间距km立方体模型节点总数/个四面体模型节点总数/个立方体模型计算时间/s四面体模型计算时间/s4.00 5135 23848 0.03 5.422.0025827864740.116.031.001156913503751.4812.030.50489339136527524.7079.970.2520123155471683390.33723.03

4.2 多震相走时联合反演及同时反演

为了验证基于四面体网格单元下的反演算法的有效性，我们选择了一个比较复杂的速度模型(图2，模型尺度为80km×80km×48km)。地表起伏约为2km，共计3757个主节点。次级节点间距为1.0km，总共有613928个节点。共剖分出18432个四面体网格单元。在z=-30km附近有一个用正弦函数生成起伏界面，最大起伏为2km； 在z=-46km附近有一个上拱的弧形界面。30个震源(图2中的灰色圆球)随机分布在10～20km的深度范围内，289个检波器(图2中的倒三角形)均匀分布在地表(注：以下所有数值模拟实验中均采用此炮—检排列)。图5给出了单炮情况下的射线路径分布图。真实速度模型如图6所示，可见水平面及垂直剖面上速度分布特征。下面讨论初至波反演、初至波与反射波联合反演、速度与反射界面同时反演。

4.2.1 多震相走时联合反演成像

联合反演中初始速度模型选用线性增加模型，反射界面为真实界面。反演结果均以与图6相同的形式给出(图7为水平切片，图8为垂直切片)。其中图7b和图8b为仅用初至P波的反演结果，图7c和图8c为初至P波和P1P反射波联合反演的结果，图7d和图8d为初至P波、P1P反射波和P2P反射波联合反演的结果，图9 (水平切片)和图10(垂直切片)分别为反演结果与真实模型的相对误差。从图7～图10可以看出，仅用初至P波进行成像在浅层可大体恢复速度场的起伏形状，但其成像深度却明显不及联合反演。在加入P1P反射波之后，由于增加了射线交错概率，同时又提高了射线密度，从水平切片结果(图7c)来看，联合反演已基本能准确地反演速度场的异常图像和异常幅度；从垂直切片的结果(图8c)来看，其成像深度明显增加；从图9c来看，模型边缘的速度场起伏的恢复效果也比初至P波的(图9b)有明显提升。加入P2P反射波之后，从两个切片的结果(图7d和图8d)来看，速度场的恢复与真实模型已基本相差无几，且从图9d和图10d可见，三种波联合反演的精度最高。此数值模拟实验表明，基于四面体网格的多震相走时联合反演可更为准确地反演出异常体形状和异常幅度，即效果明显优于单一震相的反演。

图5 射线路径示意图

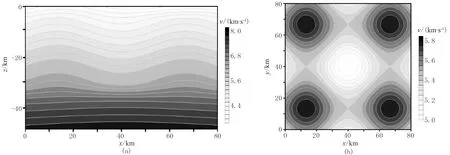
图6 三维速度模型

4.2.2 多震相走时速度和界面同时反演成像

在速度与界面的同时反演中采用的初始速度模型为向下线性增加模型，实际中初始反射界面可通过一些先验信息获得。这里初始反射界面我们选为水平界面(上界面为z=-30km，下界面为z=-47km)。对两种不同的Jacobi偏导元素进行了最大值归一化处理。图11a和图12a为初至P波和P1P反射波联合同时反演的速度结果，图11b和图12b为初至P波、P1P和P2P联合同时反演的速度结果，图11c、图11d、图12c、图12d为对应的相对误差。图13b为初至波和P1P反射波联合同时反演的上界面结果，图13c、图13e分别为初至波、P1P和P2P联合同时反演的上、下界面的反演结果。

从速度反演结果的水平切片来看，同时反演已大体恢复速度场的起伏形态，由于模型边界附近相比模型中央区域数据覆盖密度要小，而速度与界面的耦合关系又决定了界面的恢复情况必将影响速度的恢复，所以在水平切片(图11)中可看出模型中央速度恢复较好，但边缘区域恢复稍差，有些许失真，这种失真现象在双界面的同时反演(图11b、图11d)中由于较多的数据覆盖而使之得到了一些改善。

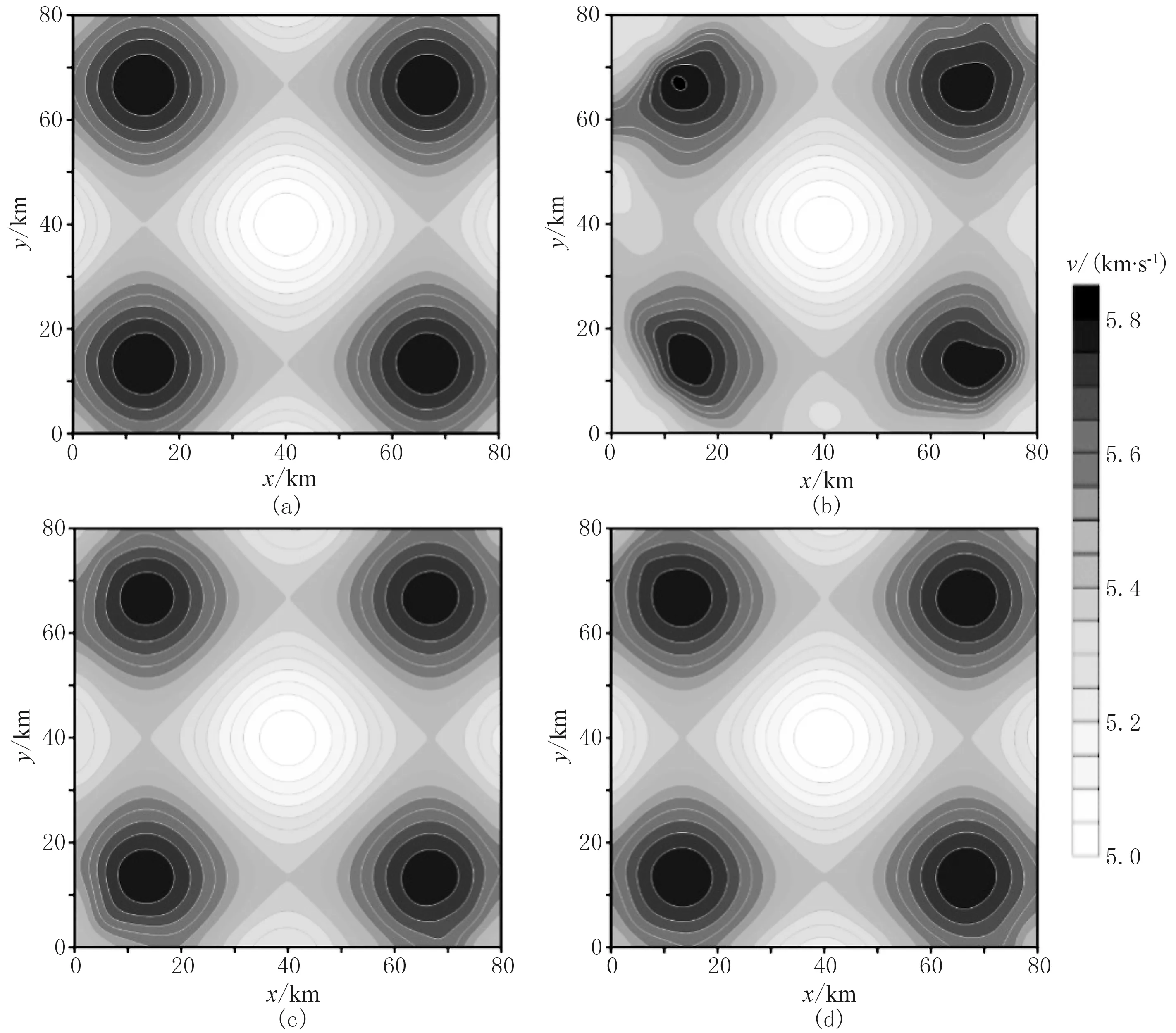
图7 不同震相走时联合反演成像的水平切片(z=-16km)

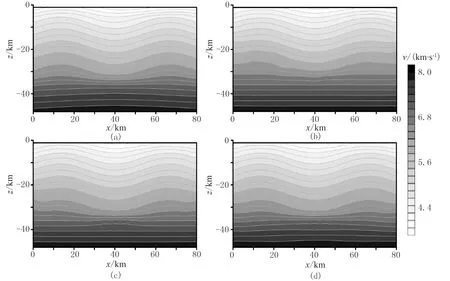
图8 不同震相走时联合反演成像的垂直剖面(y=40km)

从垂直剖面(图12)中可看出，单界面同时反演时-30km以上的速度场的起伏已经基本恢复，但在模型的边缘有些许失真(图12a、图12c)。双界面的同时反演(图12b、图12d)已经基本恢复速度场的起伏形态，相比于单界面的情况，模型边缘及下方速度场的失真情况也有了明显改善。

从图13中可见，无论是初至P波与P1P波同时反演，还是初至P波与P1P、P2P波同时反演，上界面的形态都已基本恢复。由于在双界面的同时反演中模型边界附近的数据密度大于单一界面同时反演情况下的数据密度，而大数据密度意味着对速度和界面更好的约束，也意味着更好的反演结果，这一点可从图13b与图13c的对比中看出，无论是幅值的恢复情况，还是界面形态的相似度，图13c的结果都要比图13b好。从双界面的同时反演结果中已基本可见下界面近似弧形的形态特征，但其幅值的恢复不如上界面，这是因为在上界面之上有直达波信息，可帮助更加准确地反演出速度分布，进而更好地反演上界面的形态，而处在上界面和下界面之间的区域则没有这个优势，所以在双界面的同时反演中，上界面的反演结果优于下界面。从这个数值模拟实验中可得出以下结论：基于四面体网格的同时反演得到的速度和界面结果较为可信。

图9 反演水平切片与真实模型的相对误差(z=-16km)

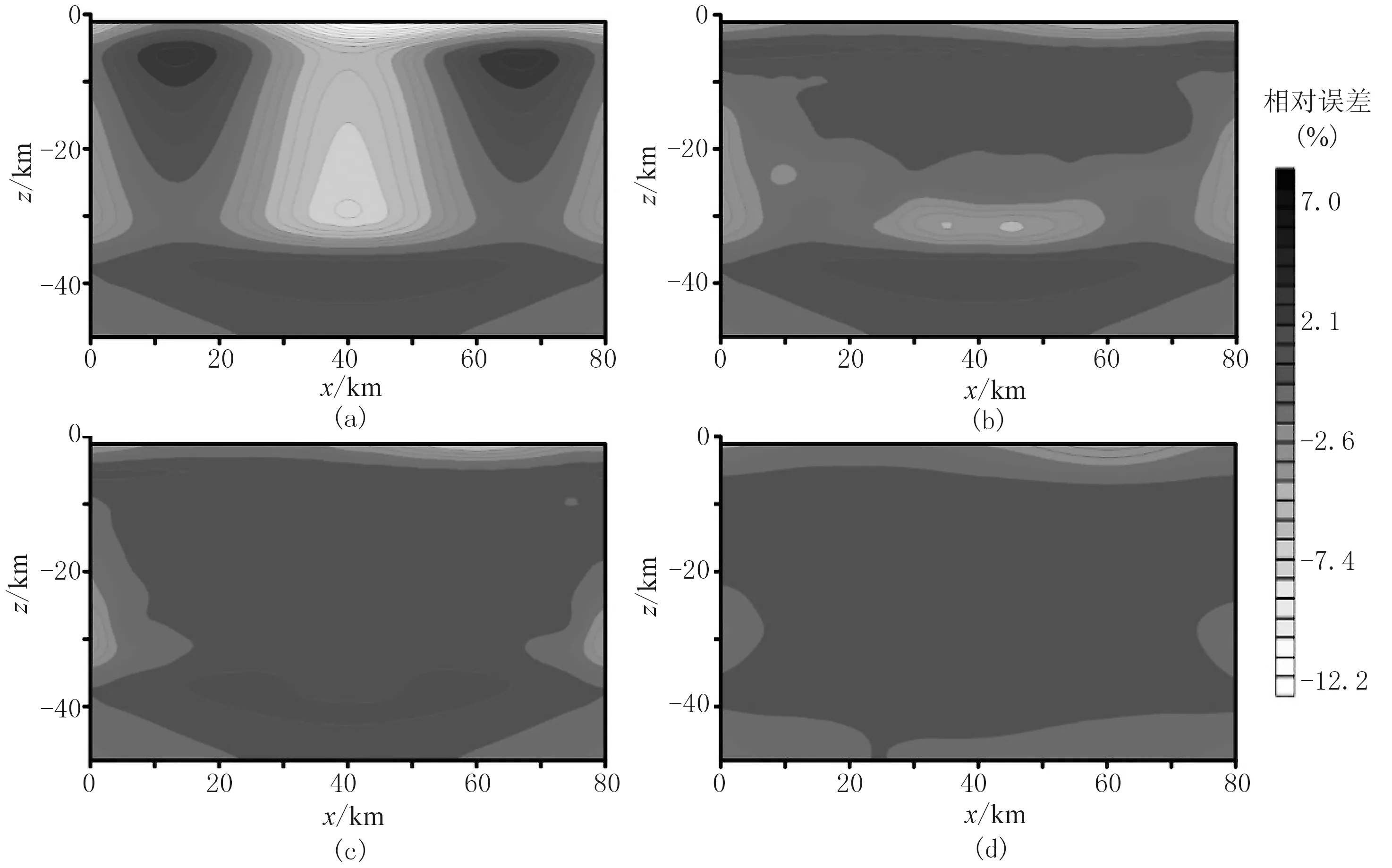
图10 反演垂直剖面和真实模型的相对误差(y=40km)

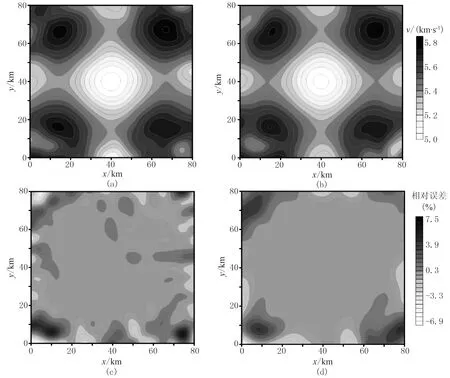
图11 不同震相走时联合同时反演成像水平切片及相对误差(z=-16km)

5 结果分析与讨论

本文基于四面体模型参数化下的多震相射线追踪技术，结合共轭梯度法求解带约束的阻尼最小二乘问题反演算法，讨论并实现了四面体模型参数化下多震相走时联合及同时反演技术。此外还对四面体模型参数化下的计算精度和CPU时间做了详细讨论，可知在总节点数目大致相同的情况下，其CPU时间远小于立方体模型下的计算时间。在同时反演中为了平衡速度和界面对走时的影响，本文对两种不同类型的Jacobi元素进行了最大值归一化处理。数值模拟实验表明，四面体模型参数化下的多震相走时联合成像技术具有很好的反演能力，能较准确地反演速度场的起伏特征和分布情况；对于速度与界面的同时反演，可较好地反演速度场的起伏特征，并可基本恢复反射界面的几何形态。在现有的地震台站分布极不均匀的情况形下，四面体网格单元可对数据密度不同的区域进行不同尺度的剖分，进而在走时反演中更显著地提高数据的利用效率，且四面体网格单元对起伏地表和异常体的拟合精度明显优于立方体单元网格，故该算法具有广泛的应用价值。