自学习优化算法对风电机组的功率控制

文 | 高鹏飞，吴浙攀，田德，赵毅

近年来，我国环境状况引起社会高度重视，寻找环境友好的可再生能源是我们的需求。风能是目前世界上技术较成熟、成本较低的可再生能源之一，发展前景较好。现在，我国已成为全球最大的风电市场，新增装机容量和累计装机容量均居世界首位。但一些因素也制约着风电的发展，例如，风的间歇性、波动性引起的机组安全和电网安全问题。因此，如何控制风电机组在多变的风速中安全高效运行成为热门话题，而神经网络正好可以解决这一问题。

目前，神经网络的研究内容主要包括神经网络理论研究、神经网络实现技术和神经网络应用研究3个方面。其中在水电方面，利用方向自学习遗传算法解决水库优化调度问题，证明该算法相对于传统遗传算法，计算速度快、收敛性好，提高了计算效率。控制方面，虽然对于神经网络及各种算法已经进行了几十年的理论研究和改进，在人工智能、自动控制等方面也取得了一定成果，但是对于风力发电行业，尤其是风电机组控制方面，神经网络及各种优化算法的结合和研究仍然很少。

为了提高过渡区域双馈式风电机组发电质量的稳定性并减少发电量损失，将自学习算法和神经网络应用到双馈风电机组过渡区控制中，与传统PID变桨控制进行对比分析，为双馈式风电机组的控制策略提供一种新的方法和思路。

运用Matlab编程软件，编写BP神经网络模型，并运用BP神经网络模型对1.5MW双馈风电机组模型的运行参数进行预测。根据预测的机组状态参数，采用一定的自学习算法，对原始的PID控制参数进行更改，得到新的控制下的风电机组运行状态参数。通过对比分析预测值和期望值间的误差以及新旧控制下的状态参数间的误差，分析该自学习算法的优化效果和适用性。

基本原理

一、BP神经网络基本原理

目前，在神经网络领域，BP神经网络是发展最为成熟的一种神经网络算法，有很多优化算法都是基于BP神经网络发展得到的。BP神经网络是一种多层的前馈神经网络。最典型的BP神经网络有3层拓扑结构，如图1所示。由图可以看出，BP神经网络包括：输入层、输出层和隐含层。各层神经元只与下层神经元有权值连接，与同层的神经元没有连接。

二、自学习算法原理

为了提高PID控制器的准确性、快速性，使得机组运行更加稳定，本文提出了一种基于BP神经网络预测下的自学习优化算法，在原有的PID控制器基础上进行改进。

自学习优化算法定义：运用BP神经网络对机组未来的特性进行预测，通过预测值判断是否提前增强或减弱变速和变矩控制。

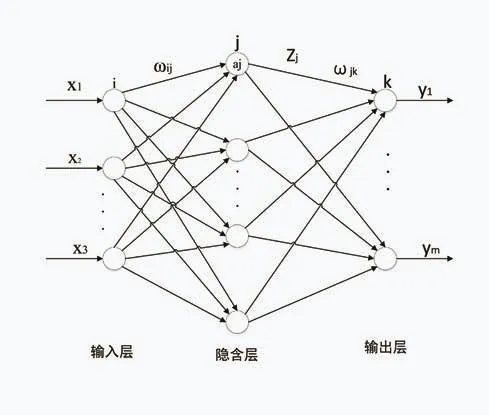
图1 典型BP神经网络拓扑结构图

（1）首先，让风电机组在原有控制策略下运行一段时间，得到一系列SCADA数据；

（2）将这些数据作为BP神经网络输入信号，进行训练，预测一定时间后的风电机组参数；

（3）对参数进行分析，当达到一定条件时，反馈给控制器一个激励，使得变桨和变速控制参数发生变化，生成一组新的控制参数；

（4）过一段时间后，再对新一组的SCADA数据进行收集；

（5）重复第二步。

将这种自学习优化算法主要运用于过渡区控制，其目的是增大过渡区风能转化效率，减小过渡区功率、转速的波动。

三、自学习算法控制策略

通过特定的BP神经网络，可以对风电机组过渡区机组特性参数进行短期预测。因此，可以通过对预测值、实时值和额定值进行一系列的计算、对比和判断，按照特定策略对原有PID控制参数进行一定时间的临时微调，增强或减缓控制动作，最终使得风电机组在过渡区的运行更加稳定。逻辑框图如图 2所示。

图2 自学习算法逻辑框图

将选择的研究数据的桨距角、转速、转矩、功率和对应的加速度作为输入信号。因为在风电机组中，主要控制量为桨距角、转矩，主要控制目标为功率和转速，因此，选择未来的桨距角、转矩、功率和转速为输出信号；同时，考虑到变桨驱动和转矩作用的滞后性，以及控制的及时性，分别选择研究数据延迟0.5s、1s、1.5s、2s后的数据作为输出期望。最终得到了超过1万个数据组，为了方便计算和程序的编写，选择1万个参数作为训练和测试样本：训练样本为8000个，测试样本（期望值）为2000个。（1）通过输入8000个相同训练信号进行训练，得到神经网络。（2）输入2000个相同测试值x，通过神经网络计算，得到预测的y值。（3）将预测值y与相对应的期望值x进行相对误差计算，并生成相对误差变化图。（4）对每一类型相对误差进行均方根计算。最终得到4类误差值。（5）对比相对误差变化图和均方根误差值，判断最优神经网络结构和初始值。

由于在0.5s时间步长下，BP神经网络功率预测的准确性更高，因此，在自学习算法控制策略中，可以使用BP神经网络所得功率预测值。而图3、图4和图5所示分别为桨距角、转矩和转速的预测值与期望值对比图。从图中可以看出，转矩和转速的预测值与期望值误差值很小，可以认为此时的预测基本准确，同样可以在控制策略计算中使用。但桨距角的误差仍然明显，且在桨距角较大时预测值普遍偏小，认为其原因是变桨控制为变增益控制，且桨距角越大增益越大。鉴于桨距角预测误差较大，在控制策略计算中不能使用桨距角预测值。

图3 BP神经网络桨距角预测与期望对比图

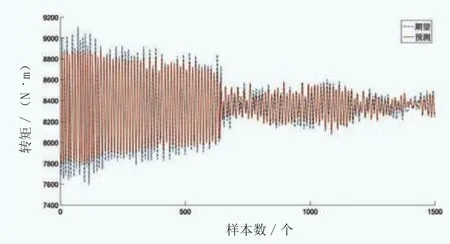
图4 BP神经网络转矩预测与期望对比图

图5 BP神经网络转速预测与期望对比图

四、自学习算法的控制逻辑

过渡区控制主要目的是为了确保风速在额定风速附近波动时，转矩控制和桨距角控制能够合理交替，使得风电机组的转速稳定在额定转速附近的同时，功率稳定在额定功率附近。

实验所用风电机组模型的额定功率为1.5MW，额定转速为188.495rad/s。因此，通过比较预测值和额定值，可以判断未来风电机组运行状态以及需要加强的控制模块。

五、训练数据风况控制结果

在自学习算法的控制策略控制下，对比新的与原有的动态功率曲线和电机转速曲线，如图6和图7所示。其中原始PID控制所得功率标准差为32885，最大、最小功率值分别为1.64MW和1.32MW，而自学习算法控制下功率标准差为27659，最大、最小功率值分别为1.64MW和1.32MW；同时，原始PID控制所得的转速标准差为2.746，最大、最小转速分别为197.05rad/s和178.986rad/s，而自学习算法控制下转速标准差为2.541，最大、最小转速分别为196.55rad/s和178.986rad/s；并且原始PID控制所得的600s发电量为250.11kWh，而自学习算法控制下600s的发电量为249.91kWh。

因此，可以认为：在原有的PID控制中引入自学习算法，理论上可以降低过渡区风电机组发电功率和转速的振荡，使得风电机组在过渡区的运行更加平稳。同时，虽然减小了一些高于额定功率的发电量，但由于提高了一些低于额定功率的风能吸收，所以在增加稳定性的同时，发电量也没有过多减少。所以，可以认为，在某一稳定风况，基于该BP神经网络下的自学习算法，能优化原有PID控制。

自学习算法控制的适用性

同一风况下，运用BP神经网络进行自学习优化控制，能使风电机组在过渡区的运行更加稳定，并且发电量不会有太大损失。接下来将验证该BP神经网络对其他风况的适应性。

一、同一训练后神经网络对不同风况的适用性

虽然基于某一特定的训练后神经网络的自学习算法，对不同的均风速风况有较好的适应性，其控制结果对原始PID控制有一定的优化作用。但在实验过程中，仍发现了一定的问题，可以对控制算法作进一步改进。

为了验证基于某一特定的训练后BP神经网络的自学习算法，对不同风况的适用性，分别输入了10m/s、12m/s、14m/s和16m/s的平均风速风况，并将其控制结果和原始PID控制下的风电机组运行参数进行对比。图8至图15即为不同平均风速风况下，引入自学习算法的控制和原始PID控制，得到的风电机组功率与转速的对比曲线图。

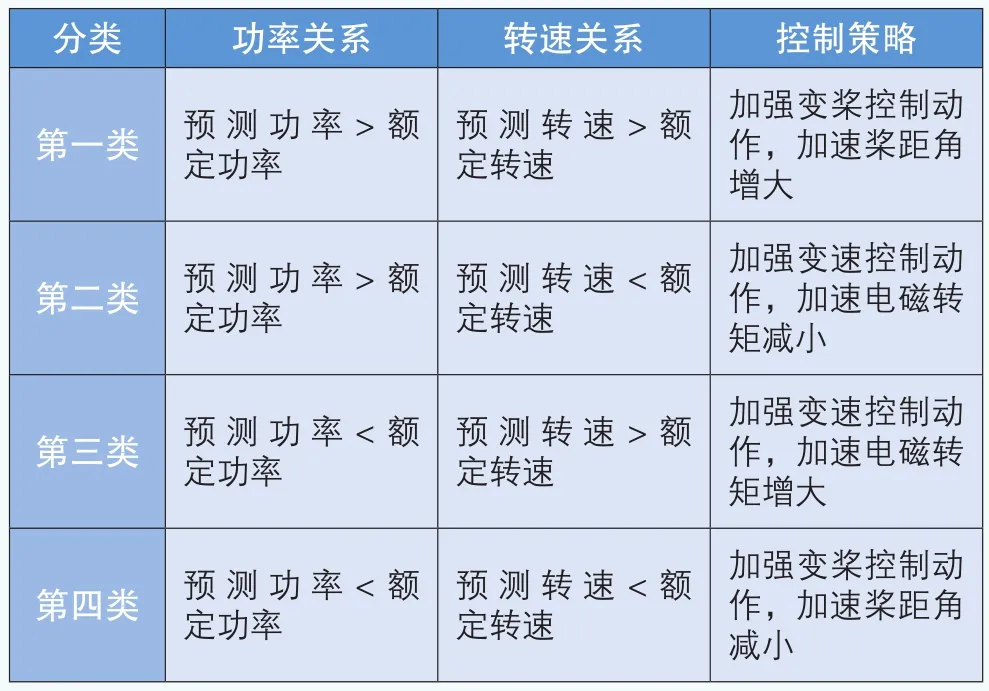
表1 控制逻辑

图6 自学习算法与原始PID控制下的功率曲线图

图7 自学习算法与原始PID控制下的运行转速曲线图

从图中可以看出，引入自学习算法的控制，对风电机组功率和转速的稳定性都有一定的提高作用。

为了更直观地验证自学习算法的优化作用，将不同均风速风况下，基于自学习算法的控制和原始PID控制的机组功率标准差、转速标准差、最大/最小功率、最大/最小转速和600s的总发电量列于表2。

由表格中数据可以看出：

（1）所有风况下，控制器在引入自学习算法后，风电机组转速的标准差都有所降低，说明基于该神经网络的自学习算法，能够优化过渡区风电机组对转速控制的稳定性。

图8 均速10m/s风况下的自学习算法与原始控制所得运行功率

图9 均速10m/s风况下的自学习算法与原始控制所得运行转速

图10 均速12m/s风况下的自学习算法与原始控制所得运行功率

图11 均速12m/s风况下的自学习算法与原始控制所得运行转速

图12 均速14m/s风况下的自学习算法与原始控制所得运行功率

图13 均速14m/s风况下的自学习算法与原始控制所得运行转速

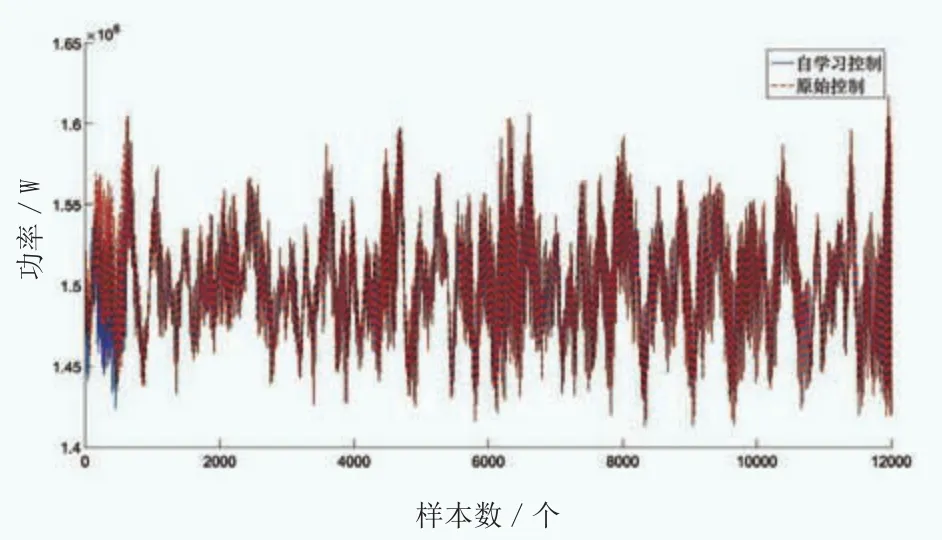
图14 均速16m/s风况下的自学习算法与原始控制所得运行功率

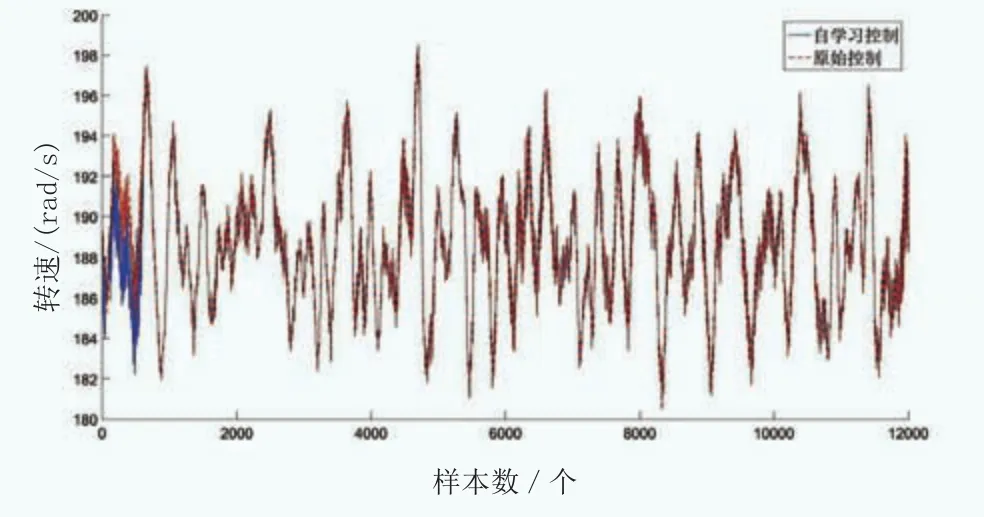
图15 均速16m/s风况下的自学习算法与原始控制所得运行转速

（2）在低平均风速风况下，由于低于过渡区风速的时间段较多，高于额定风速的时间段较少，而本文的自学习算法策略在低风速段不动作，因此，低风速段的功率与原始PID控制下的功率一致。而过渡区经过自学习算法优化，风电机组的风能利用率有所提高，因此，高风速段功率提高。此种情况，导致了低平均风速风况下，引入自学习算法的控制策略比原始PID控制策略得到的机组功率标准差略高。这也能说明自学习算法下的机组总发电量高于原始PID控制。

（3）在高平均风速风况下，由于过渡区中高于额定风速的时间段较多，自学习算法下的控制有效地降低了超额定发电的功率，因此，引入自学习算法的机组功率标准差低于原始PID控制下的机组功率标准差。这也能说明自学习算法下的机组总发电量略低于原始PID控制下的机组总发电量。

表2 不同风况自学习算法与原始控制运行参数状态

图16 特定训练后神经网络对均速10m/s风况的运行功率预测

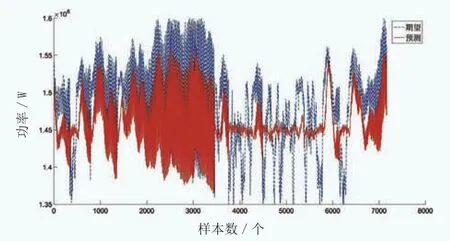
图17 特定训练后神经网络对均速12m/s风况的运行功率预测

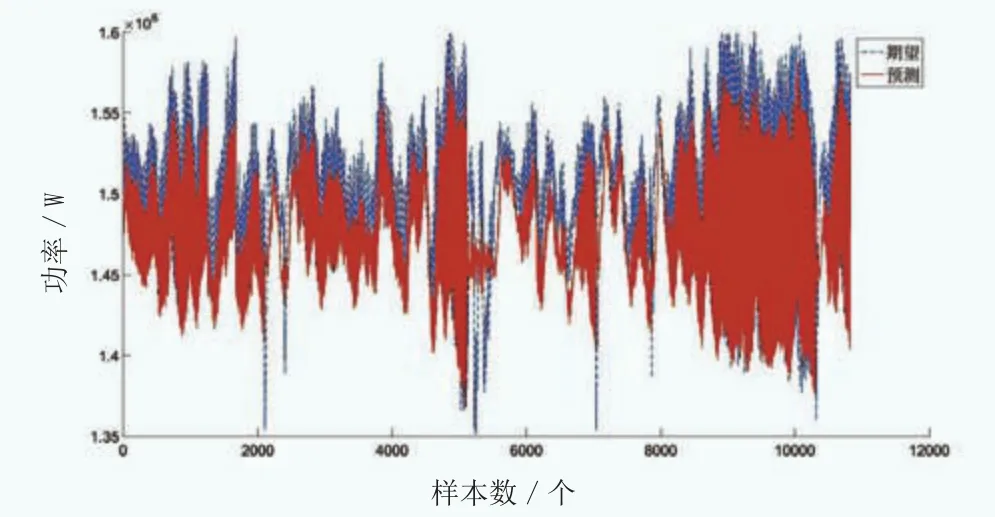
图18 特定训练后神经网络对均速14m/s风况的运行功率预测

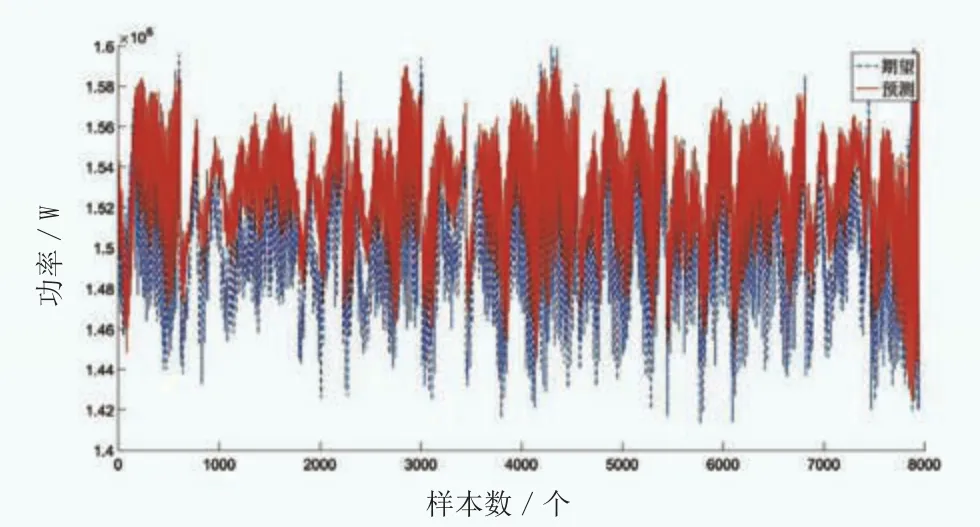
图19 特定训练后神经网络对另一均速16m/s风况的运行功率预测

以上结果可以证明，基于某一特定训练后BP神经网络下的自学习算法，对各种均风速风况的适用性较好，能有效提高过渡区机组风能利用率、降低超额定发电功率，同时增加风电机组转速稳定性。

二、再训练神经网络的自学习算法的适用性

本文采用的特定训练后神经网络，为某一16m/s均速风况下风电机组运行参数训练所得，其对10m/s、12m/s、14m/s和另一16m/s的均风速风况的功率预测能力如图16至图19所示。

可见，均风速差别越大，预测的误差越大，自学习算法对控制的优化也就越差。随着机组运行时间增加，风况变化，甚至可能导致原始PID控制下的机组运行特性反优于自学习算法控制下的机组运行特性。

因此，本文考虑针对不同的平均风速风况，进行BP神经网络再训练，得到针对不同均风速风况的训练后神经网络。运用这一系列训练后神经网络，对各自对应的均风速风况进行机组功率预测和控制。

以14m/s均速风况为例，图20和图21分别为：14m/s均风速风况训练后的BP神经网络对机组功率的预测与期望的对比折线图，以及基于该神经网络的自学习算法控制策略下的机组功率与原始PID控制下的机组功率对比折线图。

从图中可以看出，经过再训练后的BP神经网络，对相应风况的功率预测更加准确。而从控制效果来看，图21和图12有一定的差别，能够看出再训练后自学习算法的效果要优于固定神经网络的自学习算法的效果，更要优于原始PID控制效果。从数据看，此时的自学习算法控制的功率标准差为53058.94，转速标准差为2.03353，总发电量为248.27kWh。与表2中14m/s风况对应的数据相比，可以发现再训练后的自学习算法控制效果更好，功率的稳定性和转速的稳定性都有很大程度提高，而总发电量的降低主要原因是降低了超额定发电功率。

因此，可以认为，用不同风况下的机组参数训练出不同的神经网络，针对不同风况使用相对应的神经网络进行预测，能使自学习算法对原始PID控制的优化效果更好。

图20 再训练神经网络对均速14m/s风况的运行功率预测

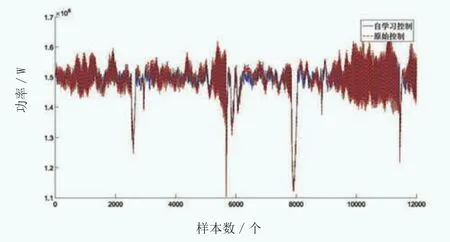
图21 再训练后均速14m/s风况下的自学习算法与原始控制所得运行功率

由于10分钟到2小时时间尺度上，风况的变化程度最小，因此，在同时考虑风况变化和计算成本后，可以采用：每间隔一段时间，运用该时间间隔中记录的过渡区风电机组运行参数对神经网络进行一次再训练，使新得到的神经网络能够在接下来的一段时间内更准确地预测机组运行参数。同时，还可以考虑昼夜风速风况变化和季风带风况季节性变化设置再训练时间间隔。

结论和展望

运用神经网络对不同平均风速风况下机组运行参数的预测，采用一定的自学习算法策略，对原始的PID控制参数进行临时调整，最终得到引入自学习算法优化控制后风电机组运行参数。通过比较自学习算法优化后的参数与原始PID控制下的参数，讨论了基于固定BP神经网络的自学习算法和针对不同风况再训练BP神经网络的自学习算法的优化效果和适用性。由于本文所用神经网络的结构相对简单，只有一层隐含层，在计算资源允许的情况下，可以考虑建立更加复杂的多隐含层BP神经网络提高预测的准确性。或者在预测阶段，对神经网络进行如遗传算法等算法的优化，以提高预测准确性。