基于传递矩阵法的超声珩齿复合变幅器设计*

□ 周梦妮 □ 张宁宁 □ 侯云盼

渭南师范学院数理学院 陕西渭南 714099

1 设计背景

超声珩齿是将超声振动切削技术应用于硬珩齿加工的一项技术，其高频振动提高了磨粒实际切削速度和切削能力，被加工齿轮的表面质量明显优于普通珩齿的表面质量［1］。从加工效益、加工质量及经济性方面考虑，超声珩齿能够达到较好的效果［2］。对于大多数齿轮与变幅杆组成的变幅器而言，变幅杆作一维纵向振动，齿轮作弯曲振动，两者振型完全不同，连接处的耦合共振关系相对比较复杂，同时齿轮是变幅器的非谐振单元。实际工作中，常用理论解析法、等效电路法或传递矩阵法来设计变幅器，这三种方法均有不同程度的适用性。文献［3-7］基于经典薄板理论对弯曲振动变幅器进行比较深入的研究，认为薄板理论本身存在不足，变幅器数学模型不完善，结果误差较大，适用范围小，很有必要对厚板振动方法进行探索。文献［8］分析了超声珩齿纵向振动变幅器三种设计方法的优缺点及各自的适用场合，为设计变幅器时选择适当的计算方法提供了理论依据。文献［9-10］应用半解析法及罚函数法研究了厚度变化对中厚环板振动的影响。文献［11-12］研究了单一变幅杆、复合变幅杆与中厚圆板组成的变幅器的动力学特征，并基于边界条件方程组求解弯曲振动变幅器。为了改善复合变幅器的性能，笔者基于Mindlin中厚板理论，推导出复合变幅器的传递矩阵，完成了圆锥形复合弯曲振动变幅器的设计，并对其振幅等做了研究。笔者的研究提供了一种合理可行的复合弯曲振动变幅器设计方法。

2 变幅器结构

复合变幅器采用了两端等长的圆锥形变幅杆［13］，结构如图l所示。d1、d2分别为变幅杆大小端直径，l1、l2分别为变幅杆大小段与中间段长度，齿轮简化为一个等厚度圆环板，其内半径a=d2/2，外半径为b，板厚为h。将齿轮安装于变幅杆小端心轴，并用螺母固定，螺母因为尺寸相对齿轮而言很小，所以在计算中予以忽略。变幅杆作一维纵向振动，齿轮在变幅杆的作用下作弯曲振动，变幅器整体作纵弯耦合振动。

3 变幅器频率方程

3.1 圆环板传递矩阵

在超声珩齿中，为了获得良好的加工质量，要求齿轮作节径数为0的轴对称横向弯曲振动。齿轮作为圆环板，在这种振动模态下其切向内力和变形必恒为0。因此，根据Mindlin中厚板理论，若不计切向应变和应力，圆环板横向弯曲振动在极坐标系中的变形函数和内力函数如下［14］：

图1 复合变幅器结构

式中：βr为圆环板转角；wr为横向位移；Mr为弯矩；Qr为剪力； Ji（δi，r）为贝塞尔函数；Yi（δi，r）为诺伊曼函数；Ai、Bi为由圆环板边界条件决定的待定常数；G为剪切模量。

δ1、δ2、σ1、σ2为引入的相关参数，表达式如下：

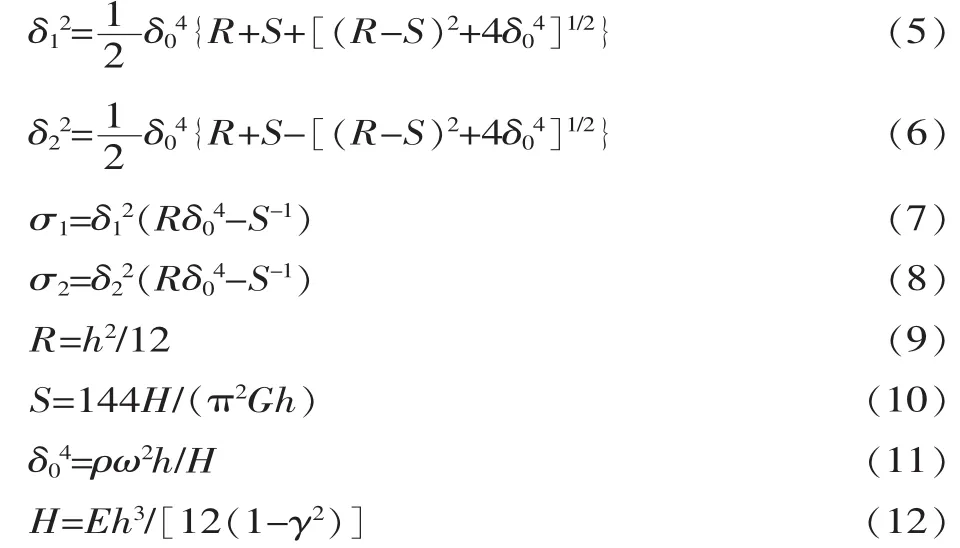
式中：ρ、ω、H分别为圆环板的密度、角频率、弯曲刚度常数；R、S分别为圆环板转动惯量和横向剪切变形影响因数；E为弹性模量；γ为泊松比。

圆环板内外表面的力学和变形分量分别用下标a、b表示，则圆环板外表面的矩阵形式为：

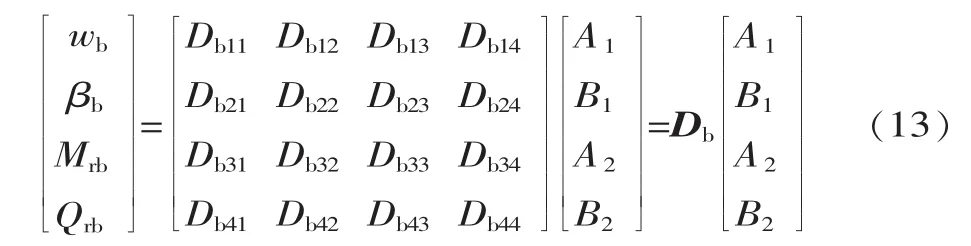
圆环板内表面的矩阵形式为：

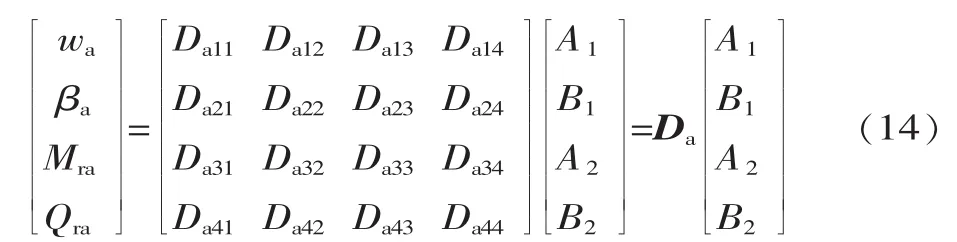
圆环板内外表面间力和变形的关系矩阵为T，于是有：

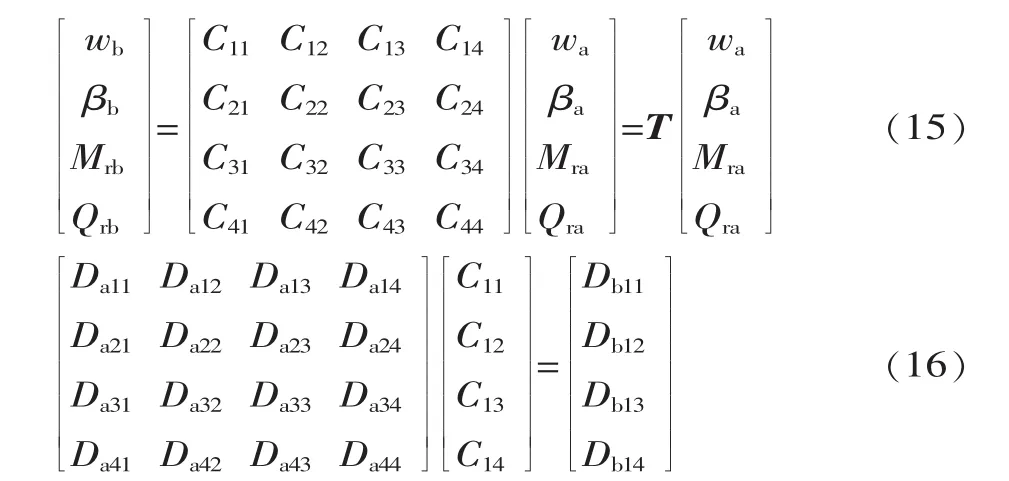
得：

3.2 变幅器传递矩阵

为方便研究，取两端等长的圆锥形变幅杆，其四端网络传输矩阵特征方程为［15-18］：

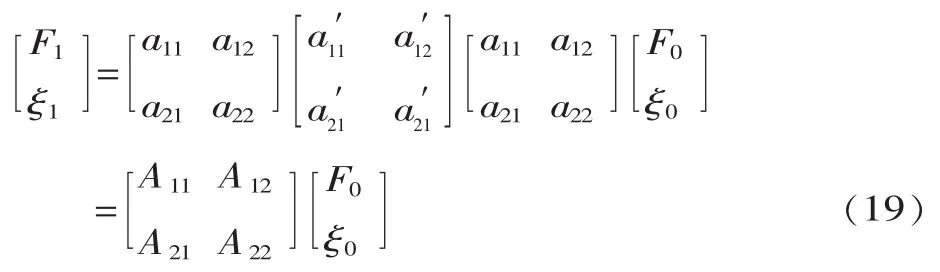
式中：F1、ξ1分别为变幅杆输出端的力和振幅；F0、ξ0分别为变幅杆输入端的力和振幅。

D为复合变幅器总传递矩阵，则有：

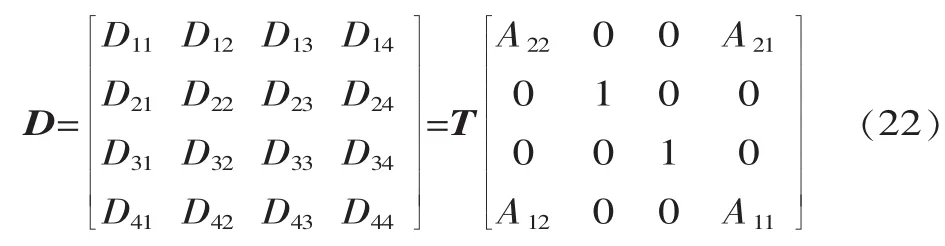
由复合变幅器数学模型可知 Mrb=0，Frb=0，βra=0，F0=0，若式（22）有解，则有：

式（23）即为复合变幅器的频率方程，若已知材料和几何参数，就可以求出系统谐振频率。根据求出的频率，可求出 A1、A2、B1、B2，再代入式（2），可求出圆环板的横向位移。

4 动力学分析

复合变幅器具体参数为d1=54 mm，d2=18 mm，l1=30 mm，a=9 mm，b=60 mm，h=18 mm， 工作频率 f=30 kHz，变幅杆中间段长度l2=20～140 mm。应用MATLAB软件绘制频率方程解的误差Δ与变幅杆中间段长度l2的关系曲线，如图2所示。由图2可以看出，解误差曲线与误差为0的直线有交点，即为频率方程的数值解，可得变幅杆中间段的设计长度l2=90 mm。

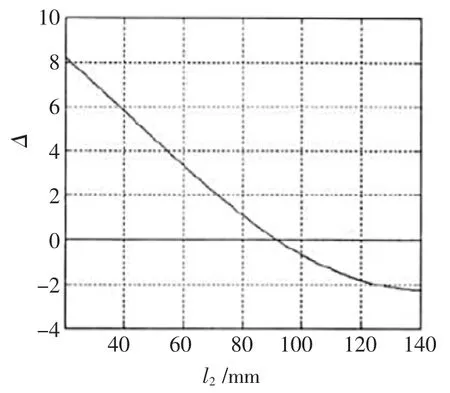
▲图2 频率方程解误差与变幅杆中间段长度关系曲线

复合变幅器材料为45号钢，密度ρ=7.8×103kg/m3，泊松比γ=0.28，弹性模量E=216 GPa，剪切模量G=84 GPa，对复合变幅器位移振幅进行计算，可以分别得出变幅杆和圆环板振幅随自身几何尺寸的变化曲线，如图3和图4所示。在此基础上，对变幅器进行ANSYS有限元仿真谐振响应分析，可以得到变幅杆和圆环板振幅随自身几何尺寸的变化仿真曲线，如图5和图6所示。由仿真分析可知，在频率为29.719 kHz时变幅杆作纵向振动，圆环板作横向弯曲振动，与理论计算基本一致，频率误差仅为0.94%，误差值在工程应用允许范围之内。

5 频率特性分析

为进一步研究复合变幅器几何参数对系统谐振频率的影响，保持其它参数不变，改变其中一个参数，将有限元分析结果与理论计算结果进行比较，见表1～表5。

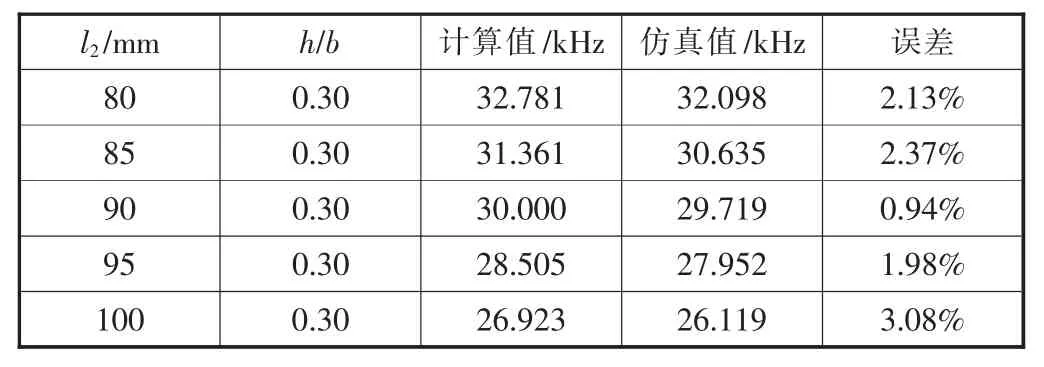
表1 系统谐振频率随变幅杆中间段长度变化数据

表2 系统谐振频率随变幅杆两端长度变化数据

由表1和表2可以看到，在保持圆环厚径比0.30不变的情况下，变幅器谐振频率随变幅杆中间段长度和大小两端长度的增大而减小，理论计算结果与有限元仿真结果比较一致，误差较小，表明理论计算的正确性。

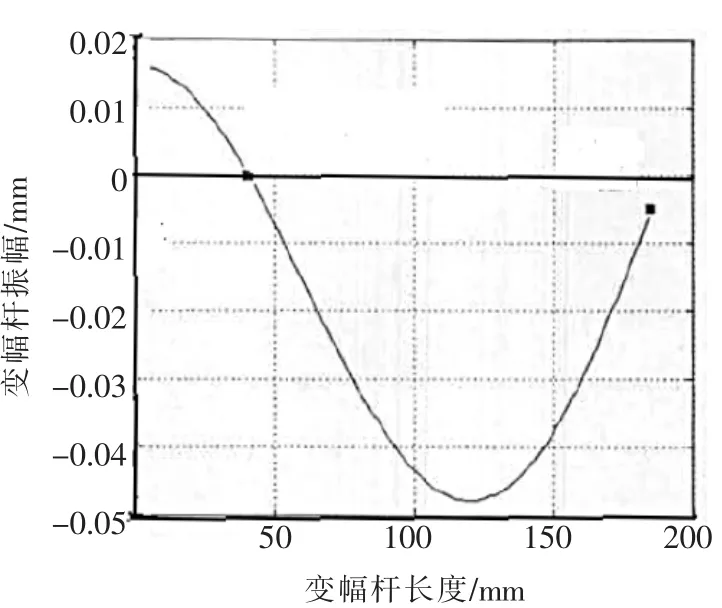
▲图3 变幅杆振幅变化曲线

▲图4 圆环板振幅变化曲线

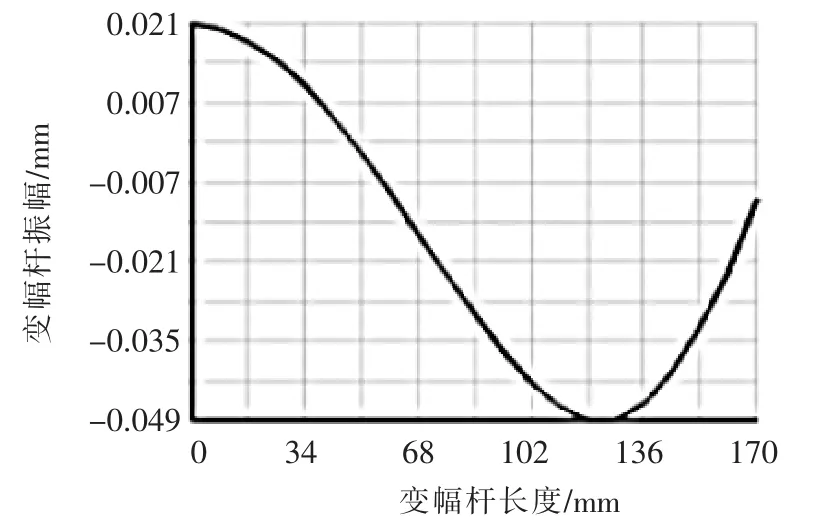
▲图5 变幅杆振幅仿真变化曲线

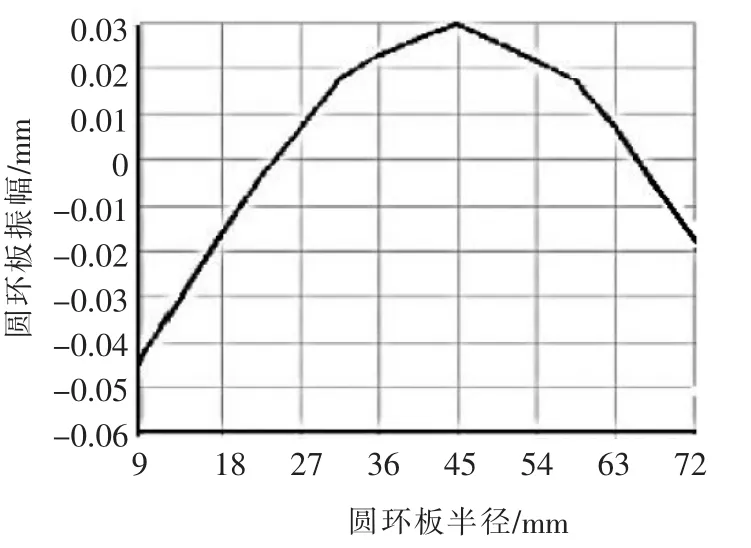
▲图6 圆环板振幅仿真变化曲线

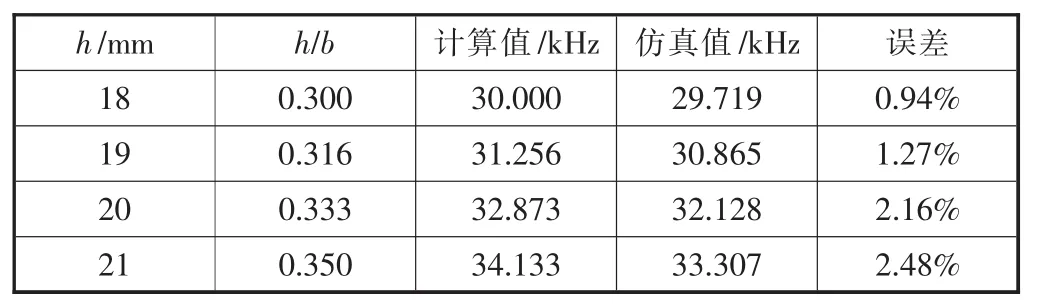
表3 系统谐振频率随圆环板厚度变化数据

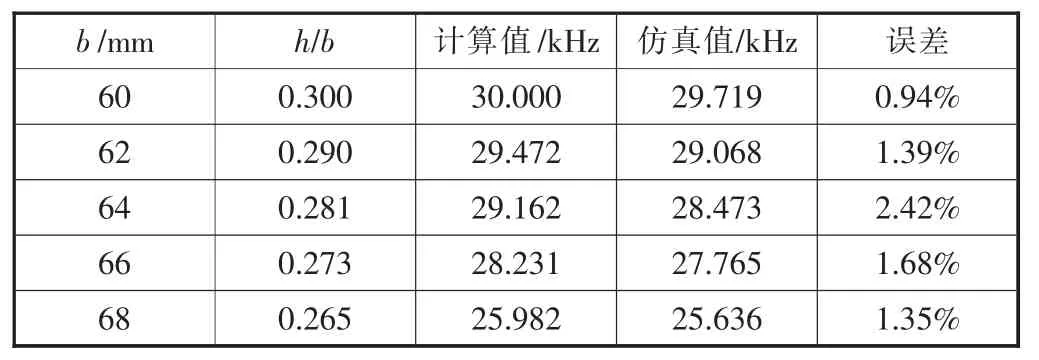
表4 系统谐振频率随圆环板外径变化数据

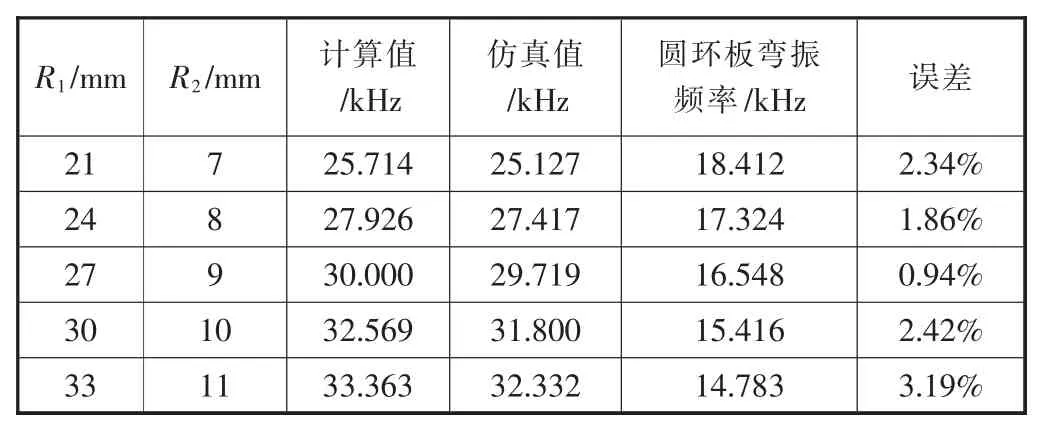
表5 系统谐振频率随变幅杆两端半径变化数据

由表3可以看到，在其它参数不变的情况下，随着圆环厚度的增大，复合变幅器的谐振频率增大。由表4可以看到，在其它参数不变的情况下，随着圆环板外径的增大，复合变幅器的谐振频率减小。由表5可以看到，当变幅杆大小端半径比值保持不变时，系统谐振频率随两端半径的增大而增大，理论计算结果与有限元仿真结果基本一致，但是圆环弯振频率与计算值及仿真值相差较大，这充分体现了非谐设计理论的正确性。

6 测试

为验证理论分析和有限元仿真结果的正确性，按照所设计的复合变幅器结构尺寸，采用45号钢加工复合变幅器简化模型，用螺母连接圆环板和圆锥形变幅杆，用阻抗分析仪进行测试。在计算机软件中选择串口为COM1，输入起始频率为29 kHz，终止频率为31 kHz，选择坐标系为对数坐标系，精度等级为Normal。扫描结束后，得到测试结果，如图7所示。由图7可知，导纳圆为单圆，对数坐标只有一对极大值和极小值，被测变幅器的导纳曲线正常，表明被测变幅器振动性能良好，其谐振频率为30.537 kHz，与设计频率误差为1.79%，误差值在工程应用允许范围之内。

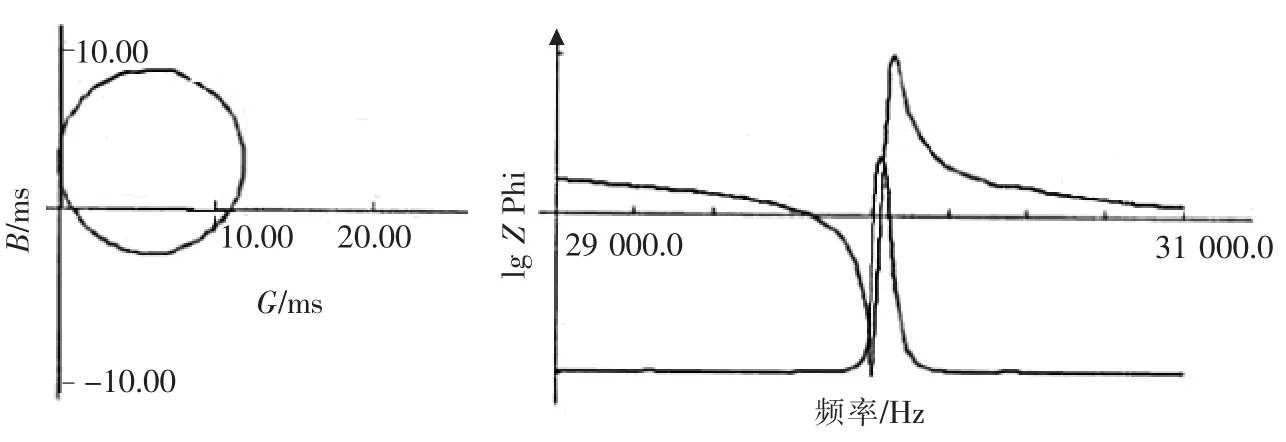
▲图7 复合变幅器测试结果

7 结论

基于Mindlin中厚板理论，推导了应用传递矩阵法计算由圆环板与圆锥形变幅杆组合的超声珩齿复合变幅器谐振频率方程，对振动特性进行了研究，分析了变幅器各参数对系统谐振频率的影响，结果表明理论计算和有限元仿真及测试结果基本一致，系统频率随变幅杆各段长度的增大而减小，随圆环板厚度的增大而增大，随圆环板外径的增大而减小，此结果可为复合变幅器的实际应用提供参考，同时也表明基于传递矩阵法设计的复合变幅器达到了生产应用要求。笔者所述方法是一种有效的变幅器设计方法，可用于超声珩齿振动系统动力学特性的研究。