间歇性生态输水塔里木河下游断面地下水位变化模拟

刘迁迁,古力米热·哈那提,王光焰,苏里坦,张 音

1 中国科学院新疆生态与地理研究所,荒漠与绿洲生态国家重点实验室,乌鲁木齐 830011 2 中国科学院大学资源与环境学院,北京 100049 3 新疆水利水电科学研究院水资源研究所,乌鲁木齐 830049 4 新疆塔里木河流域干流管理局,库尔勒 841000

作为干旱区生态系统的重要组成部分,植被主要依赖于地下水和地表水,而在塔里木河下游几乎无降水,地下水则成为维系下游生态系统的唯一水源[1- 2]。20世纪70年代初期,塔里木河下游修建人工水库,致使下游321 km河道彻底断流,地下水位大幅度下降。为解决下游地下水位过低问题,有关部门利用博斯腾湖持续高水位的有利时机,对塔里木河下游实施应急生态输水工程[3]。然而,由于实际条件的限制,无法实现输水的连续性,因此充分了解在间歇输水情况下河道地下水动态变化规律是输水生态效益评价的关键[4]。

地下水水位的估算能够很好地描述地下水流的动态变化,对水文地质研究、地下水管理等具有重要作用,常常有必要使用确定性模型重建地下水变化过程[5- 6]。塔里木河下游河道作为典型的间歇性生态输水河道,在输水-断流交替出现的过程中,其地下水渗流场运动过程中各个运动要素(水位,流速,流向等)随时间产生一定变化,具有非稳定流特性,可根据非稳定流理论进行求解。自1935年C. V. Theis[7]提出了地下水非稳定流解析解以来,国内外学者基于非稳定流原理对地下水变化模型构建的研究逐渐增多,王玉林等[8]运用非稳定流原理对抽-灌同轴非完整井承压层地下水变化过程进行了模型构建;陈志强等[9]基于非稳定流原理对岩体渗透系数进行了求解;Liggett等[10]基于边界积分方程对承压含水层非稳定流理论进行了研究;Koch等[11]基于非稳定流理论构建了耦合地表水、地下水运动关系的冰川融水径流模型;另外,Jha等[12]、Merkhali等[13]将非稳定流理论运用到河道泥沙运动过程中,得到了较好的拟合结果。

对于塔里木河下游河道,基于非稳定流理论,前人也进行了地下水变化模型构建研究[14- 16],并取得了一定进展。然而,以往的地下水模型主要适用于河岸附近,忽略了地下水运动过程中河岸距离的增加引起的地下水变化的时间滞后效应,另外忽略了潜水蒸发的影响,使得地下水变化拟合精度随河岸距离增加而逐渐降低。本研究基于前人研究成果,以塔里木河下游英苏断面地下水动态变化为研究内容,基于非稳定流理论,以水位边界条件作为初始求解条件,以余误差函数erfc(x)为求解函数,综合考虑地下水变化滞后效应及潜水蒸发作用,构建了间歇性输水河道地下水模型,并运用英苏断面C3、C4、C5、C6、C7监测井2011—2015年河岸1050 m范围内逐月地下水埋深监测数据进行了定量分析,以期构建适用于间歇性输水河道附近地下水变化过程模型,合理估算地下水变化趋势,一方面为指导塔里木河下游输水方案及生态效益评价提供科学依据,另一方面为间歇性输水河道地下水位变化研究提供模型参考。

1 地下水非稳定流计算方法

1.1 流量边界条件已知的情形

河道充水后,若河道渗漏量随时间变化值已知,则输水引起的两岸地下水位的上升值,可根据地下水动力学原理[17]进行求解。

(1)

式中,tj为时间轴刻度,其中j(j= 1,2,3,…,k)为间歇输水次数,t0= 0;S(x,tj)为离河渠x距离的点在tj时刻地下水位变化值;qj为tj时刻河道渗漏量;ierfc(λ)为补余误差函数;a为含水层压力传导系数;k为含水层渗透系数;ћ为含水层平均厚度;S(x,tj)为离河渠x距离的点在tj时刻地下水位变化值(自初始水位算起),S(x,t0) = 0。

1.2 水位边界条件已知的情形

河道充水后,如果河岸x处水位变化值已知,通常把水位变化曲线按时间轴剖分成n(n≥ 0)个小段,相邻之间的变化可看作是水位定值时的状况,从而把整个过程理解为各个微小段的叠加,利用特定水位边界时的水位计算方法[17- 18],就可以确定充水时所引起的两岸地下水位的上升值S(x,tj),即是

(2)

式中,Hj为tj时刻河岸x(x=0)处地下水位;erfc(λ)为余误差函数。

2 间断输水河道地下水交互式模型构建

影响地下水数值模拟结果不确定性的因素很多,如何从众多的因素中筛选出影响模型的主控参数是模型分析的关键[19]。基于生态组成部分相互影响,地下水变化需要综合考虑水的补给(生态输水、自补给)和消耗(地下水流动)之间的平衡[20]。其中,河道水位和流量的变化是影响地下水位动态的重要因素,一般情况下,河流水位高于附近地下水位时,将补给地下水;河流水位低于地下水位时,河渠就成为地下水的排泄出路。塔里木河下游作为典型的间歇输水河道,其地下水位变化包括两个阶段：一、生态输水阶段(图1)。此时河道渗漏主要经历以下两个过程,当地下水位低于河道底部高程时,河道产生自由渗漏;当地下水峰上升至河道底部后,地下水与河水中的地表水连成一体,也即是地下水水位边界条件已知,在这种情况下,河道将产生顶托渗漏,由于其输水特性,河道渗漏过程为自由渗漏与顶托渗漏方式交互进行。二、河道断流阶段(图1)。此时地下水缺乏持续有效的地表径流补给,地下水变化主要经历以下两个过程,地下水位侧向自补给过程,以及潜水蒸发作用引起的地下水位降低的过程。

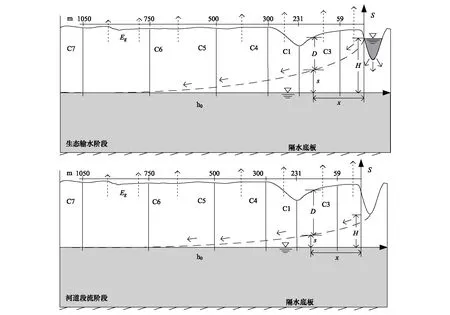
图1 英苏断面输水河道生态输水-断流交替阶段地下水变化示意图Fig.1 Ground water level changes diagram in ecological water conveyance-cutoff alternating period of Yingsu-sectionH: 地下水位;D: 地下水埋深;C3—C7: 监测井;x: 河岸距离;s: 水位变化值;S: 坐标轴; Eg: 潜水蒸发;h0: 初时水位

然而,在塔里木河下游已有的间歇性输水过程中,河道生态输水流量年际变化较大,导致不同输水阶段流量边界分布不稳定,使得实际测量过程中,生态输水流量边界的确定比较困难,工作量较大,不易求解。然而,河道附近设置有监测井,可较好地反映河道附近水位变化,易于界定水位边界。整个输水及断流过程中,在横向上仅存在侧向自补给,即高水位区向低水位区形成的侧向流,可根据公式(2)对英苏断面地下水位进行模拟,然而,随着河道距离x的增加,余误差函数erfc(x)计算结果将会逐渐减小,并且小于实际减小幅度,导致计算误差较大。因而,为提高拟合精度,需综合考虑河道距离所产生的水位变化时间误差,则有

(3)

式中,tl为距离引起的滞后时间,x为河岸与河道间的距离,u为地下水的实际流动速度。

根据达西定律,实际流动速度u=v/n=ki/n,其中,v为地下水渗流流速,n为含水介质的孔隙度,k为含水层渗透系数,i为地下水运动的水力梯度,i=Ha/xa,xa为非稳定流相邻两个渗流阶段的河岸距离差,Ha为xa距离内的水位差。然而,达西实验是基于恒定均匀渗流发生的,对于英苏监测断面非稳定地下流,水力坡度i随河岸距离呈非稳定变化,此时u已不再是断面平均流速,而是渗流断面中任一点的流速[21]。根据研究断面地下水非稳定流运动规律,将河岸带地下水渗流过程分为m个部分,此时地下水实际流速为

(4)

那么,式(3)中不同河岸距离所引起的时间滞后差则可表示为

(5)

在此情况下,地下水位变化计算公式为

(6)

式中,(Hk-H1)为模拟期间水位变化总值。

为了便于测算,将地下水水位(H)变化转换为地下水埋深(D)变化,则计算公式可表示为

(7)

式中,D为地下水埋深值,(DK-D1)为模拟期间埋深变化总值;其中S计算结果为负值表征地下水埋深减小,水位升高,正值表征地下水埋深增加,水位下降。

对于竖直方向上,潜水蒸发作用在一定程度上影响地下水埋深变化[22],此时,由于蒸发作用所引起的地下水位的变化量T为：

(8)

式中,Eg为实际蒸发量,b、c为蒸发相关系数,由实验资料确定,E0为水面蒸发强度,D0为初始地下水埋深,其中j(j≥ 1)为天数,T(0)=0。

综合公式(7)、(8),最终地下水埋深模拟值为

D(x,tj)=D0+S(x,tj)+T(x,tj)

(9)

式中,D0为初始埋深值,S与T分别为非稳定流、潜水蒸发作用引起的地下水埋深波动值。

3 研究区概况

研究区英苏监测断面(C),距离大西海子水库约61 km,位于若羌县铁干里克乡境内的其文阔尔河上,地处北纬40°25′52.3″,东经87°56′18.7″,是下游输水监测的核心位置(图2)。区域内干旱少雨而蒸发强烈,大气降水对地下水几乎不产生补给,地下水的主要补给来源是区域内的河道。已有研究表明[23],生态输水期间,塔里木河下游生态输水过程对单侧河岸影响宽度超过1000 m,并且随着输水量的增加,其影响宽度呈现增加的趋势,而河道断流期间,由于河道地下水自补给,地下水埋深波动范围也超过1000 m。因此,为全面掌握英苏监测断面处地下水埋深的动态变化情况,分别利用距离生态输水河道59、300、500、750 m及1050 m范围内的C3、C4、C5、C6、C7监测井,对河岸约1050 m范围的地下水埋深进行动态变化监测。

图2 英苏断面地理位置图Fig.2 Yingsu section location map

作为间歇性输水河道,塔里木河下游自2011年1月初至2015年12月底,共进行了五个周期共计八次生态输水工作(图3),其他时间阶段均为断流阶段。基于河道内地下水埋深在生态输水期间易达到顶托渗漏,不适宜作为水位边界求解条件,因而,本研究选取河岸59 m处C3监测井作为水位边界逐月埋深变化值初始求解条件,如图3,为C3监测井2011—2015年地下水埋深值变化图。其中,C3、C4、C5、C6、C7监测井地下水埋深初始值D0分别为3.47,4.80,5.04,5.91,7.48 m;英苏监测断面地处塔克拉玛干沙漠及库鲁克沙漠的交界地带,其岩性主要为粉砂、细砂、粉土及粉质粘土的互层,河岸附近含水介质孔隙度n约为35 %,地下水含水层渗透系数k在1—5 m/d之间;地下水压力传导系数a为575.62 m2/d;i为阶段性水力梯度,大小由不同河岸距离渗流范围及该渗流范围内非稳定流渗流变化规律决定;另外,水面蒸发强度E0为0.0075 m/d,蒸发相关系数b为0.0195,c为0.0011。

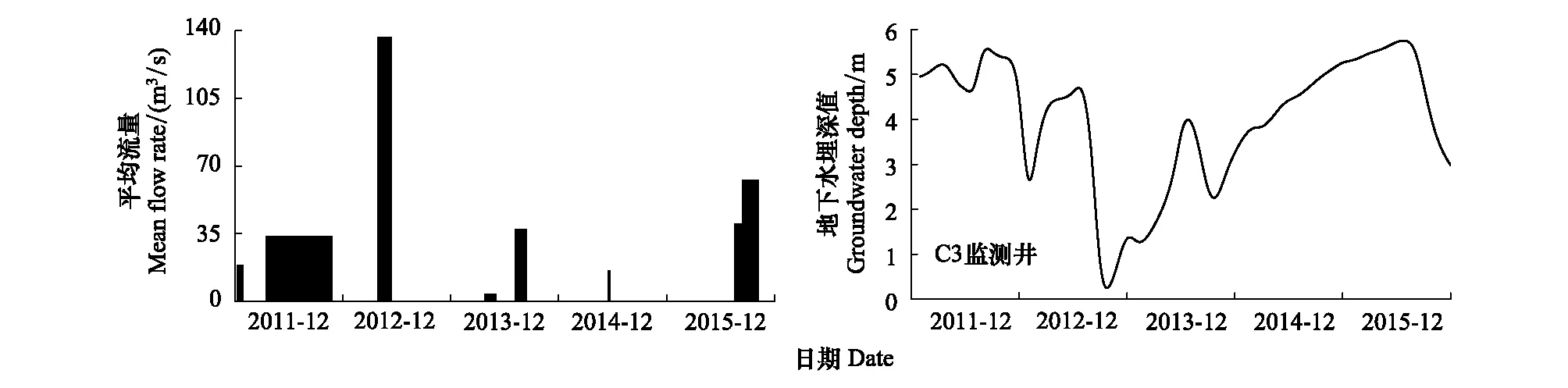
图3 2011—2015年间歇性输水过程图及河道附近地下水埋深值变化图Fig.3 Maps of intermittent water delivery process and groundwater depth change near the river during 2011—2015

4 结果与分析

4.1 地下水埋深值变化滞后期分析

由于地下水补给量的差异,随着间歇性生态输水过程的持续,塔里木河下游河道地下水位的总趋势是上升的,但离河道不同距离处的地下水位上升幅度有所不同,且波动规律具有一定的差异。研究表明,在河道输水期间,由于含水层渗透系数的限制,在短期内,临近河道地下水埋深波动较大,然而远离河道地下水埋深波动并未受到较大的影响,生态输水作用影响河岸附近地下水埋深变化会产生一定时段的滞后期,且随着距离河道的增加,滞后期增长。本研究所涉及的C3、C4、C5、C6、C7监测井分布在距河道1050 m范围内,处于河道输水影响缓冲区内,在生态输水期间,由于滞后效应,地下水埋深变化在短期内并不能对生态输水产生响应,因此在运用非稳定流理论对地下水模拟过程中,除了考虑河道附近水位边界变化之外,还需综合考虑滞后效应所引起的地下水埋深滞后变化。

通过河道距离x及含水层渗透系数k,计算出不同监测井地下水埋深变化滞后期,以2011—2015年生态输水期为时间起点,综合滞后期,得到地下水埋深变化滞后统计结果(表1)。由表1可知,在不同年份生态输水期间,C3、C4、C5、C6、C7监测井由于河岸距离的不同,地下水埋深变化滞后期达到1—13月之间,其中,2015年输水期间,C5、C6、C7监测井滞后期过长,超出计算年限,因此忽略了此段时期滞后效应计算。

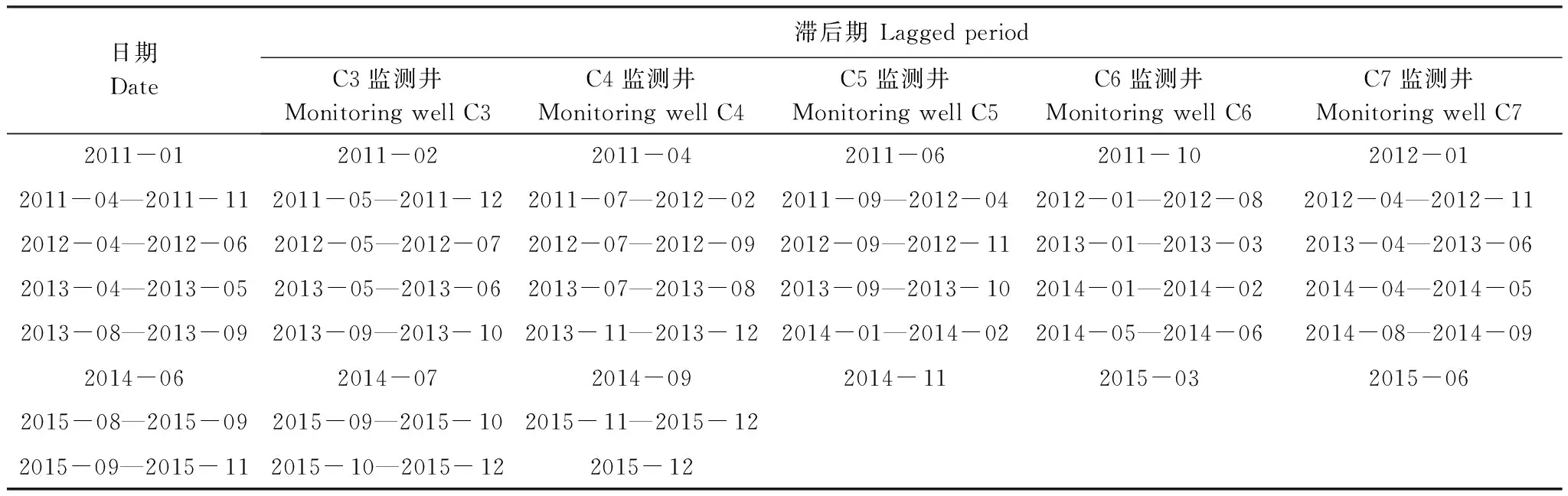
表1 2011—2015年不同监测井输水前后地下水埋深变化滞后期统计结果

4.2 地下水埋深值拟合结果分析

经过初始地下水埋深和水位边界条件设定、水文地质参数赋值、不同河岸距离地下水埋深变化时间滞后效应界定、潜水蒸发条件设定、模型校验、参数微调、公式计算,最终完成了英苏监测断面地下水埋深变化模型构建。以C4、C5、C6、C7监测井初始埋深值、2011—2015年河道附近C3监测井地下水埋深变化值为初始求解条件,运用公式(5)、(6)非稳定流计算模型,潜水蒸发计算模型进行模拟计算,得到C4、C5、C6、C7监测井2011—2015年逐月埋深变化及潜水蒸发变化模拟结果(图4)。

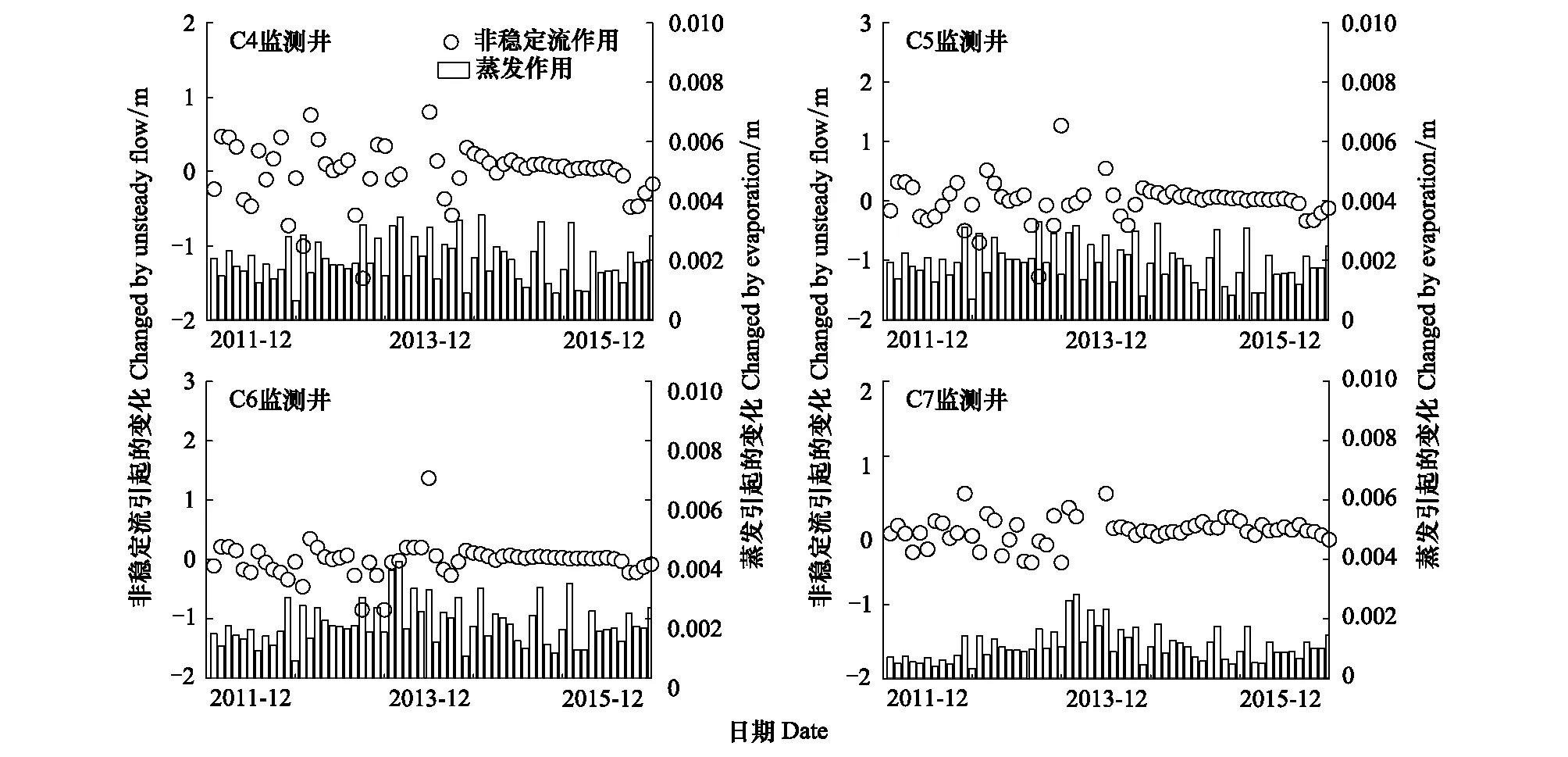
图4 2011—2015年非稳定流及蒸发作用引起的地下水埋深值变化模拟值Fig.4 Simulation of groungwater depth changes caused by unstedy flow and evaporation during 2011—2015

由图4可知,生态输水作用对地下水埋深月变化及年变化影响较大,引起的地下水埋深变化值较大,并且波动明显;基于综合考虑生态输水期间地下水埋深变化滞后效应,不同河岸距离不同监测井地下水埋深变化波动趋势具有一定的差别,但总体变化趋势一致。潜水蒸发作用在短期内对地下水埋深变化影响作用较小,然而在多年时间序列上对地下水埋深变化总影响值不可忽视,在2011—2015年期间,潜水蒸发作用引起河道附近地下水埋深变化累加平均值超过0.1 m,在一定程度上对地下水埋深产生了影响。其中距离河道1050 m处C7监测井潜水蒸发作用变化累加值为0.066 m,距离河道750 m处C6监测井潜水蒸发作用变化累加值为0.111 m,距离河道500 m处C5监测井潜水蒸发作用变化累加值为0.118 m,距离河道300 m处C4监测井潜水蒸发作用变化累加值为0.122 m,表明随着河岸距离的减小,潜水蒸发作用对地下水埋深的影响逐渐增强,且随着时间的累积,以及生态输水引起的河道附近生态恢复效应的突显,该影响作用将持续增强。

运用公式(7),将C4、C5、C6、C7监测井地下水埋深初始值与地下水埋深变化模拟值(图4)累加计算,得到2011—2015年地下水埋深最终模拟结果。综合英苏断面不同监测井2011—2015年逐月地下水埋深实测数据,得到地下水埋深变化拟合-实测对照图(图5)。由图5可知,对于各监测井埋深变化实测值,在时间序列上波动变化明显,在间歇性输水过程中地下水埋深值呈现阶段性增减,总体表现为生态输水阶段地下水埋深减小,断流阶段地下水埋深增加。对于各监测井埋深变化模拟值,总体变化趋势与实测值一致,在河道断流期间,由于地下水自补给及潜水蒸发作用,模拟得出的地下水埋深值逐渐增加;在生态输水期间,由于河道内地表径流对地下水补给作用,河道附近地下水埋深值总体呈现减小的趋势。综合考虑表1滞后效应所对应的滞后期进行埋深变化求解,有效的获取了生态输水期间不同监测井地下水埋深滞后变化规律,得到较好的拟合变化结果,地下水埋深模拟值在输水月份及其对应的滞后月份均符合实测变化趋势。

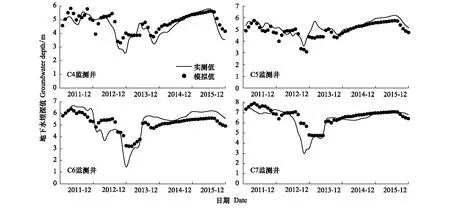
图5 2011—2015年地下水埋深值拟合结果Fig.5 Simulation of groungwater depth during 2011—2015

4.3 地下水埋深拟合精度分析

为研究地下水拟合效果,对模拟结果进行精度分析。图6为地下水埋深观测值与模拟值检验结果图,可以反映模拟值偏离实测值的程度。由图可知,数据主要集中在拟合曲线周围,没有明显偏离的情况,表明塔里木河下游断面尺度地下水埋深观测值与模拟值表现出较好的相关性。

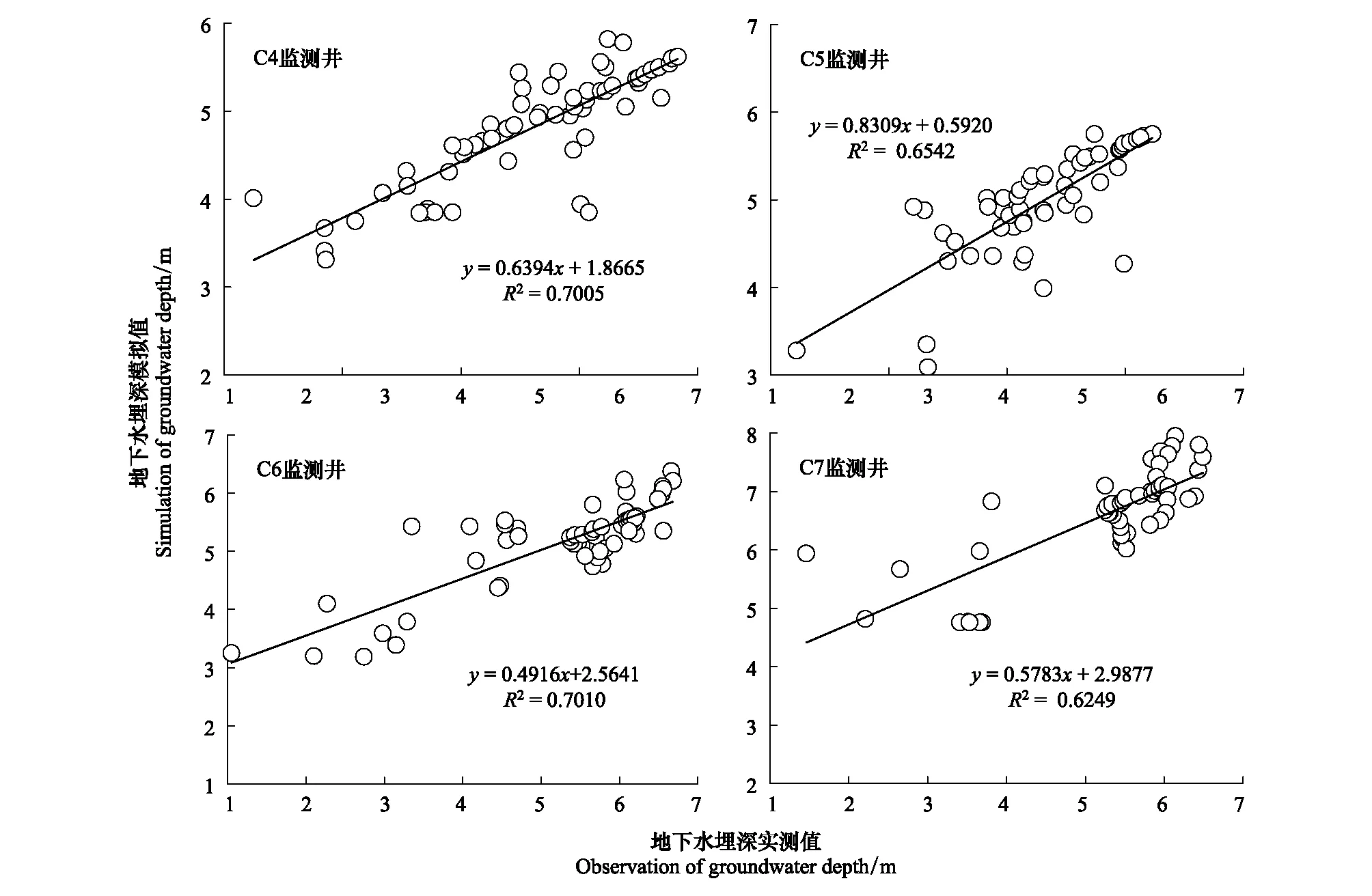
图6 2011—2015年地下水埋深观测值与模拟值有效性检验Fig.6 Validity test of observation value and simulation value of groundwater depth during 2011—2015

表2为地下水埋深拟合精度统计结果,其中确定系数R、相关系数R2反映拟合精度,平均绝对误差(mean absolute error,MAE)表征模拟值偏离实测值的大小,平均相对误差(mean relative error,MRE)为平均绝对误差与平均模拟值的比值,用以表征拟合结果的准确性水平[24- 25]。对于C4、C5、C6、C7监测井地下水埋深模拟值与实测值相关关系,在P<0.01置信区间内均达到显著性水平;对于不同监测井其确定系数R值均大于0.791、相关系数R2均大于0.625;另外,对于平均相对误差MRE,均不超过13%。结果表明,基于地下水非稳定流理论及潜水蒸发模型拟合结果的相关性较好,表明以河道为基点的地下水非稳定流运动及潜水蒸发作用是影响沿岸地下水变化的诸多环境因子中最敏感的因子。

表2 C4—C7监测井地下水埋深值拟合精度统计结果

*表示在P<0.01水上平显著相关

另外,随着距离河道的增加,确定系数R值、相关系数R2逐渐减小,地下水模拟精度逐渐降低,其中,C5、C7监测井拟合精度较C4、C6监测井低,主要原因是随着距离河道的增加,影响地下水埋深变化的随机性因素逐渐增多。其中C5监测井分布于距河道约500 m处,为植物分布比较集中的位置,植物生长及蒸散发作用对地下水埋深变化产生一定的影响;C7监测井分布于距河道约1050 m处,距离河道较远,受到多元方向的地下水补给与排泄作用,影响模拟精度。但是总体上,对于河道附近1050 m范围内地下水埋深模拟,已达到了所需精度要求,对于间歇性输水河道地下水埋深变化状况模拟具有重要意义。

5 结论与讨论

本研究采用非稳定流理论,以水位边界条件为自变量,并综合考虑潜水蒸发及生态输水期间地下水埋深变化在时间及距离尺度上的滞后效应,对塔里木河下游断面尺度单侧河岸1050 m范围内地下水变化进行模拟,得出以下结论：

(1) 生态输水期间,在短期内,临近河道地下水埋深波动较大,而远离河道地下水埋深波动并未受到较大的影响,生态输水作用影响河岸附近地下水埋深变化会产生一定时段的滞后期,且随着距离河道的增加,滞后期增长,其中C4监测井滞后期最短,C7监测井滞后期最长。

(2) 非稳定流作用对地下水埋深月变化及年变化过程中影响较大,引起的地下水埋深变化值较大,并且波动明显;潜水蒸发作用在短期内对地下水埋深变化影响作用较小,然而在多年时间序列上对地下水埋深变化总影响值不可忽视。综合分析表明,以河道为基点的地下水非稳定流运动及潜水蒸发作用是影响沿岸地下水变化的诸多环境因子中最敏感的因子。

(3) 通过本研究所应用的非稳定流理论及潜水蒸发模型,在河岸300、500、750、1050 m处拟合精度R2分别达到0.701、0.654、0.701、0.625,达到了地下水模拟精度的要求,对塔里木河下游断面尺度上地下水恢复状况研究具有重要的理论意义与参考价值。

输水效益的显现是一个漫长的过程,地下水的响应和下游植被的生态响应在一个大的空间和时间尺度上将逐步显现[26]。英苏断面作为塔里木河下游核心监测带,自河道处开始至1050 m范围内,依次分布有胡杨-柽柳-草甸混合带、草甸带、草甸-荒漠混合带、半荒漠带,且不同植被类型所需地下水埋深值有一定的差异。其中,当地下水埋深3—3.5 m时,胡杨-柽柳林分布最大[27];当地下水埋深在3—5 m时,最适合草本植物生长;当地下水位低于6 m时,物种的多样性均匀度丰富度迅速降低[28]。运用非稳定流理论对地下水位变化模拟,在已知河道附近地下水埋深变化值、间歇性输水时间以及初始地下水埋深情况下,可对河道附近地下水影响范围内任意位置地下水埋深变化进行模拟,结合不同植被类型生态响应期,进而对生态效益进行评估,在一定程度上可提高生态评价的效率。

然而,在实际计算中,由于观测不准或极端气候因素、多元地下水补给及排泄等外因的缘故,地下水模拟结果与实际测量结果存在一定的偏差[29]。本研究侧重测算间断歇性输水过程及潜水蒸发作用对地下水位变化影响,忽略了其他因素对地下水位的影响,同时本研究是基于断面尺度研究,在一定程度上限定了区域内地下水补给及排泄的边界。因此在今后的研究中需要进一步细化模型,增加更多的影响变量以提高模型的精度,同时伴随今后监测精度的提高,获得相关参数的精确性会更高。另一方面,下一步研究过程中,将在以地下水模拟为主的生态水文研究的基础上,增加地下水-植物耦合关系,以更好的建立生态输水-地下水-植物生态效益快速评价体系。