湖南栎类天然次生林林分空间结构对灌木物种多样性的影响

朱光玉, 徐奇刚, 吕 勇

中南林业科技大学, 长沙 410004

物种多样性是群落功能复杂性和稳定性的重要量度指标,是影响生态系统功能和服务发挥的关键因素之一[1- 3]。林下植被是森林生态系统的重要组成部分,它对改善土壤理化特征、提高水源涵养能力、发展更高级群落等方面具有十分重要的作用[4- 5]。乔木层作为森林生态系统的主体,其林木的空间结构特征将对林分空间异质性产生明显的影响,导致林下植被生长微环境发生变化,从而影响林下植被多样性[6]。而森林的空间结构是森林经营过程中最有可能调控的因子[7],因此研究森林空间结构对林下物种多样性的影响具有重要的实践指导意义。

惠刚盈指出森林结构由空间结构和非空间结构组成：林分密度、树种组成、直径分布、树高分布等为森林的非空间结构;林木的点格局及其属性的空间分布即为森林的空间结构[8]。而现阶段众多学者对林下植被物种多样性的研究大多集中在海拔、土壤、坡度、坡向等环境因子[9- 13]与林分密度、树种组成、年龄结构等非空间结构因子[14- 17],针对林分空间结构对林下植被多样性影响的研究较少。黎芳等以16块典型样地为对象,运用单因素方差分析及灰色关联度分析法,分析了兴国县马尾松飞播林林分空间结构对林下植被多样性的影响[6],灰色关联度分析法可以在很大程度上减少由于信息不对称带来的损失,并且对数据的要求较低,适用于样本容量较少的情况,但它需要对各项指标的最优值进行现行确定,存在一定程度的主观性,且林分结构相对简单,样地分布比较集中立地类型相对简单。对于复杂林分,其林分结构是如何影响林下灌木物种多样性的值得深入研究。

栎类(Quercusspp.)是我国亚热带地区天然林的主要林分,第八次全国森林资源清查结果显示,从优势树种来看,栎类林的面积和蓄积分别占全国森林的10.15%和8.76%,具有突出的研究价值。栎类是湖南的一种典型森林类型,且以天然次生林为主,其林下植被状况并不乐观,为探索有效提高林下植被物种多样性的途径,本文以湖南栎类次生林典型样地为对象,运用Pearson相关系数、多元线性回归分析和典型相关分析法分析林分空间结构对单个及多个物种多样性的影响,全面深入地探索林分空间结构对林下物种多样性的影响机理。为提高林栎类次生林灌木物种多样性森林经营决策提供参考与理论依据。

1 研究区概况

湖南省地处中国中南部,长江中游,108°47′—114°15′E,24°38′—30°08′N,东西宽667 km,南北长774 km;土地总面积约为21.18万hm2,其中林地面积1300万hm2,森林覆盖率59.57%,活立木蓄积5.05亿m3;海拔24—2099 m,大部分地区海拔高度在100 m至800 m之间。属大陆性中亚热带季风湿润气候,全省年平均气温为16—18℃之间,年日照时数为1300—1800 h,无霜期长达260—310 d;年平均降水量在1200—1700 mm之间,雨量充沛,水热充足。土壤主要以红壤和黄壤为主,其次为紫色土和冲积土。研究区主要植被,乔木为栎类(Quercusspp.)、马尾松(Pinusmassoniana)、樟树(Cinnamomumcamphora)、鹅耳枥(Carpinusturczaninowii)等;灌木为山茶(Camelliajaponica)、鹿角杜鹃(Rhododendronlatoucheae)、箬竹(Indocalamustessellatus)、细枝柃(Euryaloquaiana)、尖连蕊茶(Camelliacuspidata)等。

2 研究方法

2.1 样地设置与调查

采用典型取样法,分别在湖南龙虎山林场、芦头林场、青羊湖林场、八大公山自然保护区栎类天然次生林中设置49块20 m×30 m的样地。并在每块样地建立起的直角坐标系内,划分为6块10 m×10 m的乔木小样方,并按照顺序进行编号,依次为1、2、3、4、5、6。对小样方内胸径大于5 cm的乔木进行每木检尺,逐株测量其胸径、树高、冠幅、坐标等因子。在样地的4个角上设置4块2 m×2 m灌木小样方和4块1 m×1 m草本小样方,对角线交点处设置1块灌木小样方和1块草本小样方,共计5块灌木小样方和5块草本小样方,调查记录植被的种类、数量、盖度等因子。样地基本情况调查因子包括样地的经纬度、海拔、坡位、坡度、坡向、土壤类型、凋落物厚度、腐殖质厚度、群落类型、林分起源、郁闭度和林龄等。部分样地调查情况如表1所示。

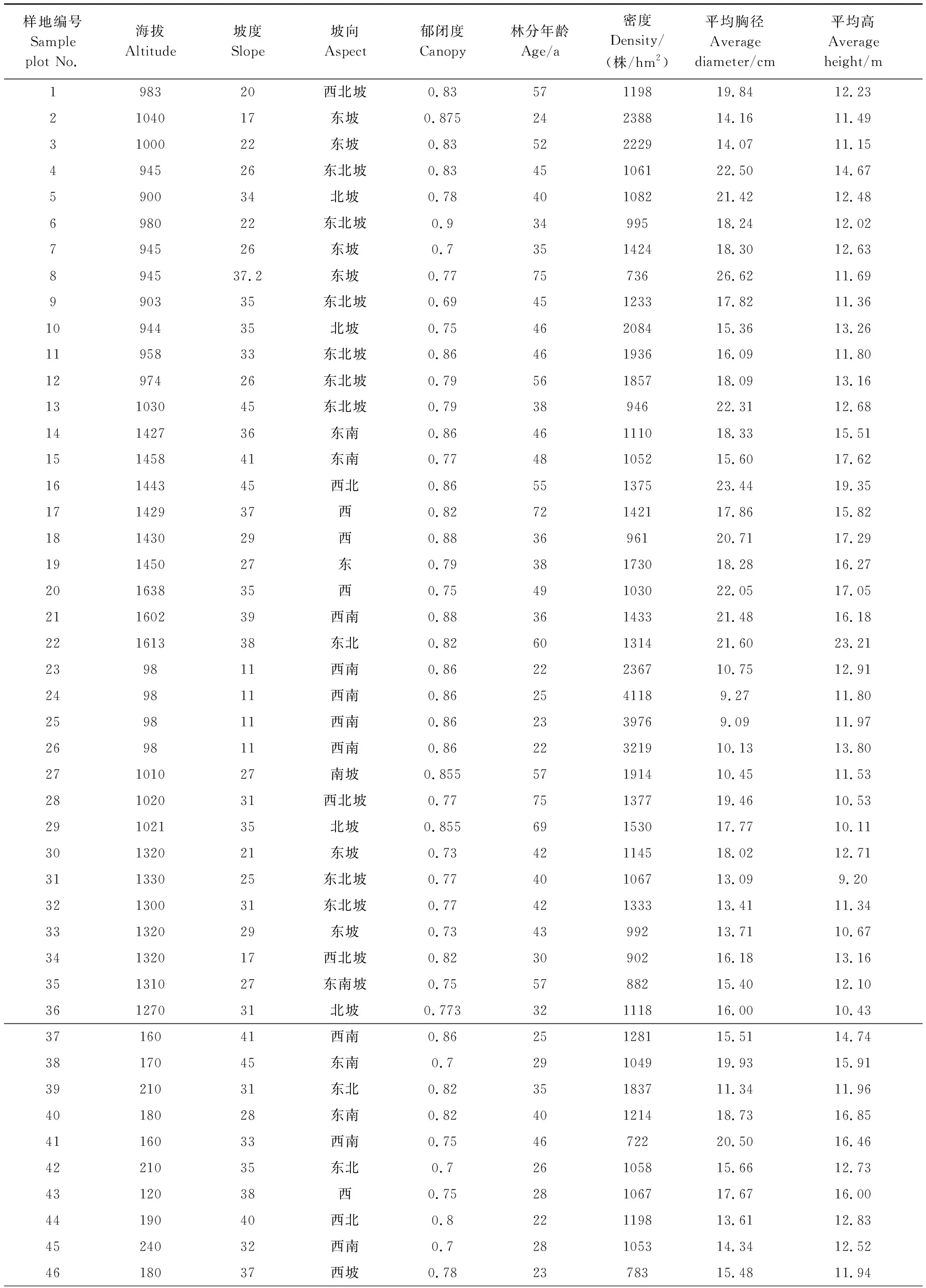
表1 样地的基本情况

续表样地编号Sampleplot No.海拔Altitude坡度Slope坡向Aspect郁闭度Canopy林分年龄Age/a密度Density/(株/hm2)平均胸径Average diameter/cm平均高Average height/m4718038东北0.728941 16.69 12.96 488035西0.625211106 13.56 12.96 4920031西0.75211160 16.12 13.19

2.2 林分空间结构指数的计算

本文采用聚集指数、混交度和开敞度作为表达林分空间结构的参数[18]。由于在计算林分平均大小比数时,林分中的每一株林木既被选择作为参照树,同时也作为其他林木的相邻木,它不能反映出林分整体的空间优势程度[19],因此本文并未选择大小比数来表达林分空间结构。同时为避免边缘效应对林分结构的影响,设置5 m缓冲区。本研究空间结构单元数n取4。

聚集指数R用以描述林木空间分布格局,即最近邻单株聚集的平均值与随机分布下的期望平均距离之比,其公式为：

(1)

式中,ri为第i株林木与其最近邻木之间的距离,N为样地林木株数,F为样地面积[20]。

混交度M是表达树种空间隔离程度的指数。其被定义为在与参照树组成空间结构单元的相邻木中与参照树属于不同树种的林木所占的比例。

(2)

式中,当参照树与相邻木非同种时,Vij=1,反之=0[21]。

开敞度B：被定义为参照木i到最近4株相邻上层林木的水平距离与该株上层林木高度的比值之和。

(3)

式中：Dij为参照树i到第j株相邻木的距离,Hij为第j株相邻木的高度[22]。

2.3 林下灌木物种多样性的计算

量化物种多样性的指数有很多,计算方法与表达的意义也各有不同。本研究选取以下常用的物种多样性指标[23-25]：

丰富度指数采用Margalef指数:

DM=(S- 1)/lnN

(4)

多样性指数采用Auclair & Goff指数:

(5)

均匀度指数采用Pielou指数:

(6)

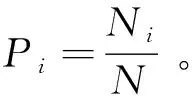
灌木层的物种多样性的重要值公式如下：

重要值Ni=[相对多度+相对盖度+相对频度]100/3。

2.4 林分空间结构与林下物种多样性相关关系分析

本研究利用Winkelmass与Excel 2016分析工具,计算固定样地林分空间结构指数与物种多样性指数,并基于此,利用R 3.4.0分析林分空间结构与林下植被多样性的相关关系。

(1)Pearson相关系数

采用Pearson相关系数判断林分空间结构指标与物种多样性指标之间的单因素相关性。计算公式：

(7)

(2)多元线性回归分析法

由于林下物种多样性可能会受到林分空间结构各个指标的综合作用,因此,本研究采用多元逐步回归法筛选出对物种多样性影响最大的关键指标,分别以每个灌木物种多样性指标为因变量,林分空间结构指标为自变量进行线性逐步回归,利用回归统计效果检验指标(AIC,P,R2)选择最优模型,不仅可以揭示多个自变量对因变量的影响,还可以用回归方程进行预测和控制[26]。

(3)典型相关分析

为探究空间结构指标和林下灌木多样性指标两组变量整体之间的相关性,在本文研究中,使用典型相关分析(Canonical Correlation Analysis)构建综合指标,提取相关性最大的线性组合并得到相应的典型相关系数,以此来判断两组变量之间的相关性[26]。选取两组变量,一组变量为混交度M、聚集指数R和开敞度B,代表林分空间结构的各个方面,一组变量为Margalef指数、Pielou指数和Auclair & Goff指数代表林下灌木物种多样性的各个方面。在此基础上,利用主成份分析的思想,分别在两组变量中选取若干有代表性的综合变量ui和vi,使每一个综合变量都是原变量的线性组合,即：

(8)

在线性组合ui和vi的方差为1的约束条件下,使它们的相关系数达到最大。据此求出典型载荷aij和bij,并得到典型相关变量ui和vi及其相关系数,进而揭示两组变量之间的关系。

检验假设H0：r=0

检验第r个典型相关系数的显著性时,作统计量：

(9)

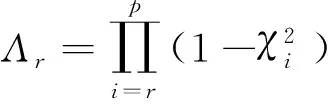
Qr近似服从χ2分布,自由度为(p-r+1)(q-r+1),p与q分别代表两组变量的变量个数。若在给定的显著性水平α下,Q大于等于临界值,则拒绝原假设H0,至少可以认为第r对典型变量具有相关性,相关系数为r,且为显著[27]。

3 结果与分析

3.1 各项指标的计算结果与分异特征

由49块样地的林分空间结构指标与林下灌木物种多样性指标统计信息可以看出,湖南栎类天然次生林各个样地间混交度、开敞度和林下灌木丰富度的变化较大,变异系数CV分别为40.82%、30.2%和46.42%(表2)。

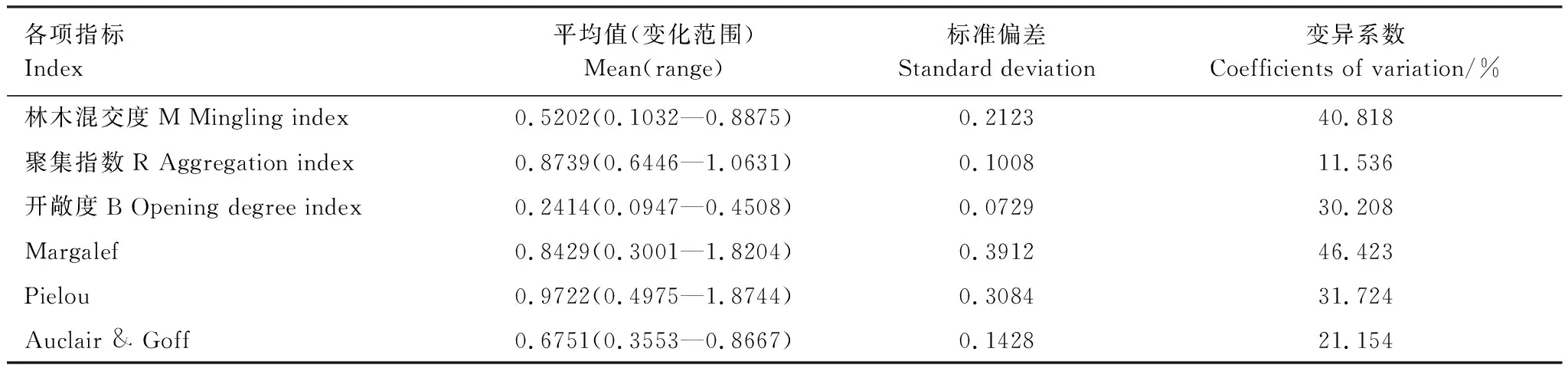
表2 49块样地林分空间结构与林下物种多样性指数的统计信息

3.2 林分空间结构与灌木物种多样性的单因子相关分析

对典型样地计算所得的空间结构指数(混交度、聚集指数、开敞度)和林下灌木的物种多样性指数的计算结果进行Pearson相关性检验,所得结果如下：

*：在0.05水平上显著相关;**在0.01水平上显著相关

表3结果显示,Margalef指数与3个空间结构指标无显著相关关系。Pielou指数与混交度呈显著相关(P<0.05),相关系数为0.3041,与其余指标无显著相关关系。Auclair & Goff指数也只与混交度呈显著相关,相关系数为-0.4347,与其余指标无显著关系。由于Auclair & Goff多样性指数是一个逆向指标,因此,林下灌木的多样性与混交度是正相关,会随着林分混交度的提高而提高。

3.3 多元逐步回归分析结果

由于林分空间结构各个指标会综合作用于林下灌木物种多样性,因此在单因素分析的基础上,以灌木物种多样性指标为因变量,林分空间结构指标为自变量,采用多元线性逐步回归法建立逐步回归方程,筛选出影响林下灌木物种多样性的关键指标。如表4所示,多元线性逐步回归结果如下：(1)Margalef指数的多元逐步回归方程拟合效果不佳,无法通过显著性检验。(2)Pielou指数的回归方程通过显著性检验(P<0.05),模型选择了混交度,聚集指数和开敞度加入方程,说明其主要受到乔木层树种空间隔离程度,林木分布格局和林下光照条件的影响。(3)在Auclair & Goff指数方面,选择了混交度,开敞度加入回归方程。2个指数都选择了多个空间结构指数作为主要影响因子且都受到混交度的影响。2个回归模型的决定系数R2均不高,分别为0.1631和0.2328,说明被筛选进入方程的林分空间结构仅能解释灌木物种多样性的部分变异,物种多样性指数会受到除林分空间结构外其他因素的影响。

表4 灌木物种多样性多元逐步回归方程

3.4 林分空间结构与灌木物种多样性的典型相关分析

典型相关分析能够将林分空间结构和物种多样性单一指标之间的联系扩展到两组变量之间的相互依赖关系,为探究两组变量整体上的相关性,运用R 3.4.0对林分空间结构与灌木物种多样性的典型相关分析结果如下：

表5典型相关系数及其检验

Table5Thecanonicalcorrelationcoefficientsanditsstatisticaltests

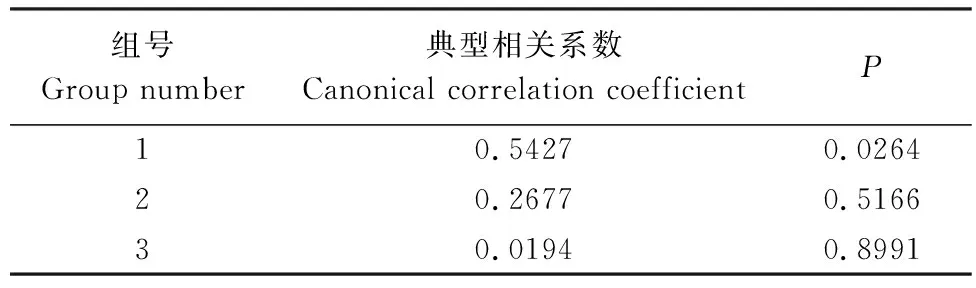
组号Group number典型相关系数Canonical correlation coefficientP10.54270.026420.26770.516630.01940.8991

由表5可知,经检验,在α=0.05的水平上,第一组典型变量通过了典型相关系数检验,且其典型相关系数为0.5427,说明林分空间结构指标与林下灌木物种多样性指标在整体上具有较高的相关性。

从表6可得出第一对典型变量的线性组合是：

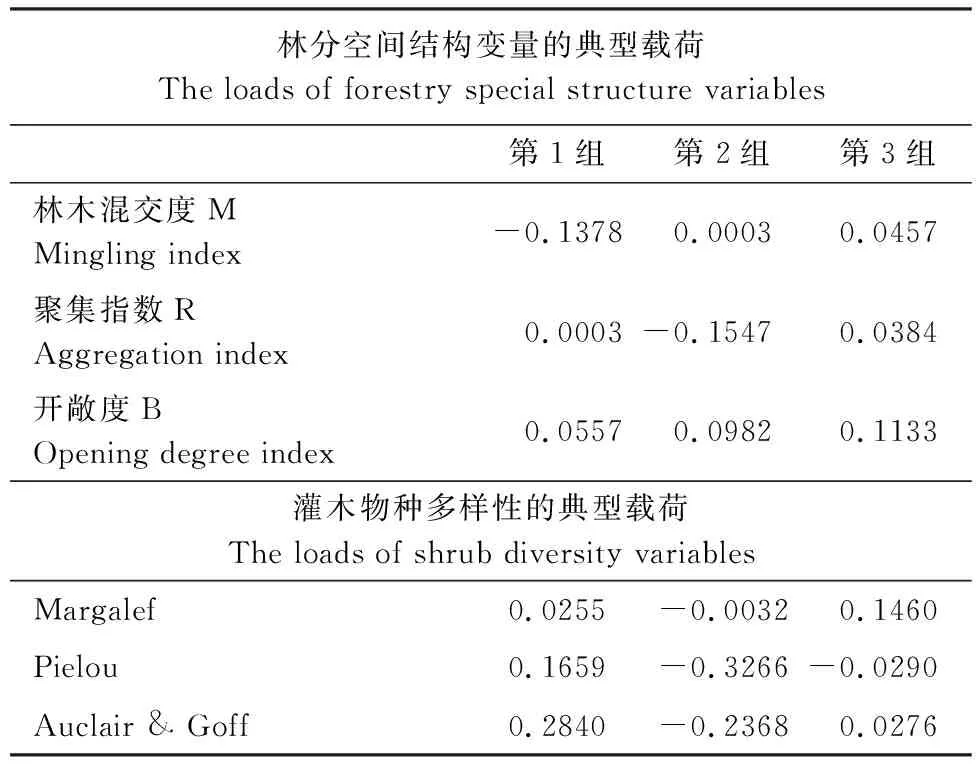
表6 三对典型相关变量的载荷

在第一对典型变量u1,v1中,u1为栎类天然林林分空间结构指标的线性组合,其中混交度M、开敞度B的载荷较大,分别为-0.1378,0.0557,说明在对林下灌木物种多样性的影响力上,乔木层林木的混交程度和林分透光度占主导地位。v1是林下灌木物种多样性指标的线性组合,其中具有较大载荷的变量是Pielou指数和Auclair & Goff指数,说明林下灌木的多样性指数与均匀度指数对乔木层林分空间结构指数较为敏感。将原始数据带入第一对典型变量中,可得到典型变量u1、v1的得分,根据每一块样地的得分值画出得分散点图。

由图1可得,u1和v1的得分散点近乎分布于一条直线上,两者之间呈现较明显的线性关系,这说明典型相关分析能够较好地说明林分空间结构和林下灌木多样性之间的相关关系,林分空间结构指标与林下灌木物种多样性指标在整体上的相关性显著。

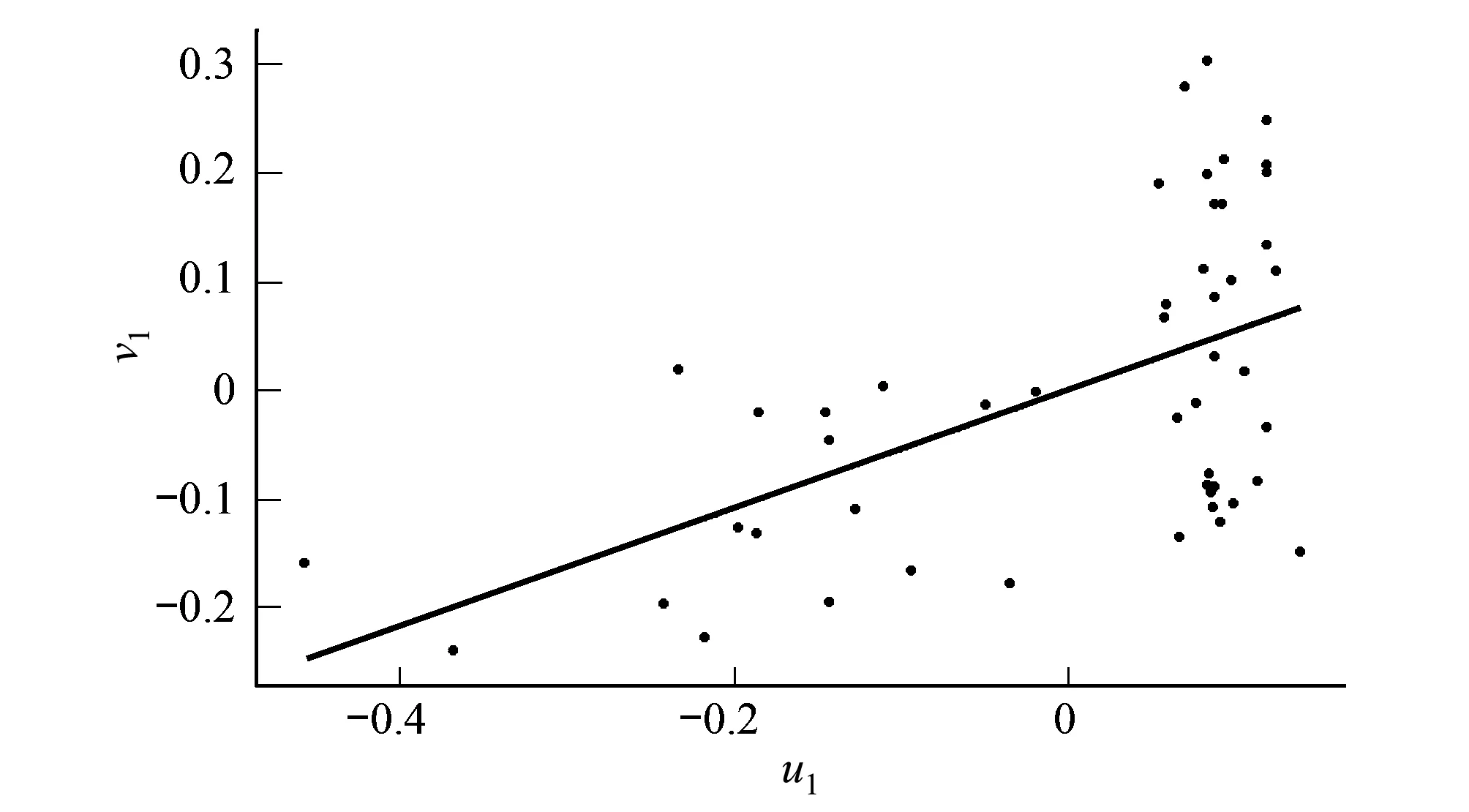
图1 空间结构与林下灌木多样性典型相关得分图 Fig.1 The score of canonical correlation between spatial structure and shrub diversityu1:林分空间结构指标线性组合得分值 The score of linear combination of spatial structure indices;v1林下灌木物种多样性指标线性组合得分值The score of linear combination of understory shrub diversity indices

4 结论与讨论

4.1 讨论

研究结果显示栎类天然次生林的混交度是影响其林下灌木物种多样性的主要因素。如图2所示,混交度与Pielou指数、Auclair & Goff指数都呈现明显的线性关系,随着混交度的增大,Pielou指数相应增大,Auclair & Goff指数相应减小,说明林分乔木层的混交程度越大,其林下灌木的物种均匀度与多样性程度都会随之增大(Aulair & Goff指数是一个逆向指标),这与黎芳等[6]的研究结果一致,可能是由于在混交林中,林分混交度的高低影响着乔木层各个树种的竞争程度,不同树种的生态位在一定程度上会互相抑制,为林下灌木的生长释放了营养空间。多元线性逐步回归结果与典型相关分析结果显示聚集指数也是影响林下灌木物种多样性的关键指标,上层林木的空间格局分布的不同会影响其枯落物与林下光斑位置,导致林下灌木均匀度也随之改变,聚集指数越大表明林木分布越均匀,相应地,其林下灌木的均匀度指数也就越高。研究结果也显示开敞度作为表达林下光照条件的指标,开敞度越大,林下光照条件越好,但其林下灌木的均匀度与多样性却反而相应减小了,这可能是由于在调查的样地中,开敞度高的样地,其乔木层林木的树高均不高,而树高是表现样地立地条件优劣的关键因子,也就意味着相应样地的立地因子如：海拔、坡向、土壤厚度、枯枝落叶厚度等可能并不有利于其林下灌木的生长。同时,2个多元线性回归模型的决定系数R2均不高,这也表明了林分空间结构指标只能解释其林下灌木物种多样性的部分变异,其他影响因子如林分非空间结构以及生境因子对林下灌木的生长也起着至关重要的作用。因此在以后的研究中,可以综合考虑环境因子,林分空间结构与非空间结构因子,选择更加显著的特征来提高模型的拟合效果,以期更深入地认清影响林下物种多样性的关键因子。

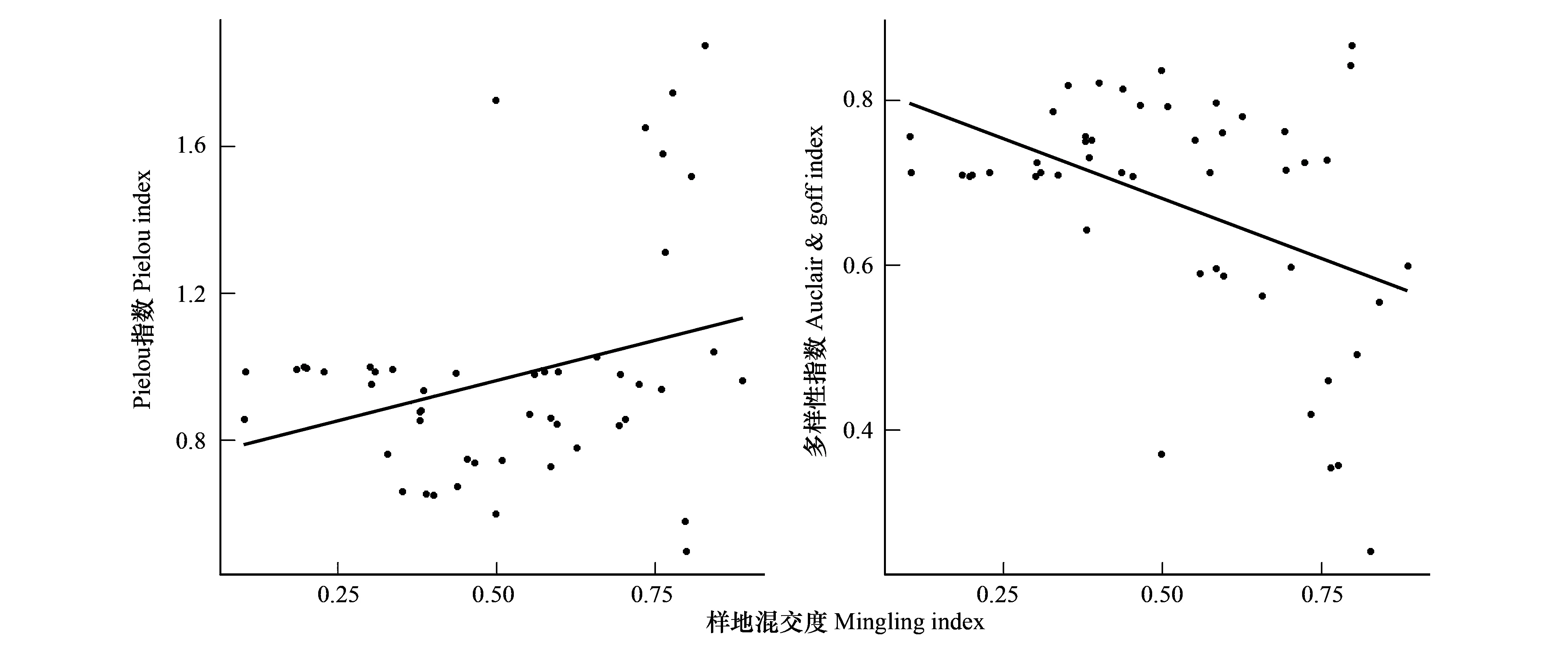
图2 混交度对林下灌木物种多样性的影响Fig.2 Effects of Mingling Index on Shrub diversity

研究表明,Pearson相关分析,多元线性逐步回归分析和典型相关分析能够全面直观地表现出林分空间结构指标与林下灌木物种多样性之间的单因素相关性以及在整体上的综合影响,但3种统计方法均建立在变量之间为线性关系的假设上,尚未探究变量之间的非线性关系,若试图更深层次地探究林分空间结构与林下植被物种多样性之间的相关性,可以尝试建立非线性回归模型或选择机器学习算法进行进一步的研究。另外,在典型相关分析中,如若变量个数与样本含量比例不合适,变量个数比例偏大,样本容量不够,必然会影响典型相关系数的显著性,因此如果选择典型相关分析来研究林分结构与林下物种多样性之间的相关性,解释变量的数量受到了限制并且研究的外业调查成本将成为难以回避的问题。

4.2 结论

对于栎类次生林而言,乔木层林分空间结构中的混交程度和林木分布状况是影响林下灌木物种多样性的主要因子,其中混交度的影响最大;乔木层林木混交程度越高,其林下灌木物种的均匀度指数与多样性指数越大;乔木层林木分布状况越均匀,其林下灌木的均匀度指数越高。因此,欲提高栎类天然次生林下灌木物种多样性,应选择以调整树种结构为主,综合考虑林木空间分布格局的调整方案。