数控外圆磨削中切磨次数的算法及编程

2018-09-19孙秦超

精密制造与自动化 2018年3期

关键词：等距砂轮整数

孙秦超

（陕西秦川格兰德机床有限公司陕西宝鸡 721300）

数控外圆磨削中，当磨削部位轴向长度大于砂轮宽度且径向磨削余量较大时，一般采用切纵复合磨削方法，可大量节省加工时间，提高加工效率。所谓切纵复合磨削：即多次等距跳档切入磨削，去除较大径向余量，剩余很小径向余量时，采用纵磨方式磨削至最终尺寸。

每次切入磨削要求砂轮要有一定的重叠量，方能保证多次切磨后不留或保留微量的切痕和棱线，要保证纵磨达到精度要求，就需要自动计算切磨次数和跳档距离，然后进行编程加工，本文就算法和编程方法进行以下讨论。

1 磨削要求说明

根据磨削工艺，切纵复合磨削有以下要求：

1.1 磨削起点和终点

根据工艺，在纵磨外圆时砂轮在磨削部位两端都要有一定的磨出量，且砂轮在两端位置要有一定的停留，两端的磨出量和停留时间不一定相同，根据工件情况而定。磨出量大的一端，停留时间可少一些，反之则相反。并非砂轮边缘与工件两端对准开始磨削，否则磨削完成后，两端头部直径大小会与中间不一致，存在误差。

如遇台阶轴，砂轮在一端可能就没有磨出量，那么此时停留时间就长一些，而另一端留有磨出量，停留时间可以少一些，两端停留时间并不相等。由此可见，磨削编程时起点和终点并不能完全由图纸尺寸而定，而是操作工根据磨削需要确定，再配合停留时间达到预期目的。

实际操作中，操作工分别将砂轮移动调整到左右两端，留出一定的磨出量，记录左右两端的轴向座标 Z_L和 Z_R,或者利用用户自定义画面上的坐标捕捉功能，自动记录两端Z坐标。

1.2 砂轮切入重叠量

如果按照砂轮宽度跳档多次切入磨削，由于砂轮磨损，使每次磨削量有差异，另一方面在两次切入磨削砂轮交界处会留有一个棱线，是不利于后面的往复纵磨和达到最终精度，这些都会产生磨削不利因素。

为了解决以上问题，可以使砂轮跳档距离小于砂轮宽度，等距跳档，每次切入磨削时有一个重叠量就可以解决棱线问题。当然重叠量越小，切入次数会越少，效率就越高，等距跳档可以解决砂轮磨损问题。

要实现最小的重叠量，又要等距跳档，这还与跳档距离、砂轮宽度、磨削范围相关，并非独立确定的量，有待于后面计算。

1.3 跳档距离和切入次数

从以上分析可见，等距跳档切入可以保证砂轮磨损状况基本良好。重叠量d、跳档距离L、切入次数n三个物理量相互关联，存在最优算法，需要进一步讨论计算。

2 计算方法

假设砂轮宽度为W、左磨削起点座标为ZL、右磨削终点座标为ZR（ZR＞ZL）、砂轮重叠量为d、跳档距离为L，切入磨削次数为n(正整数)，如图1所示。

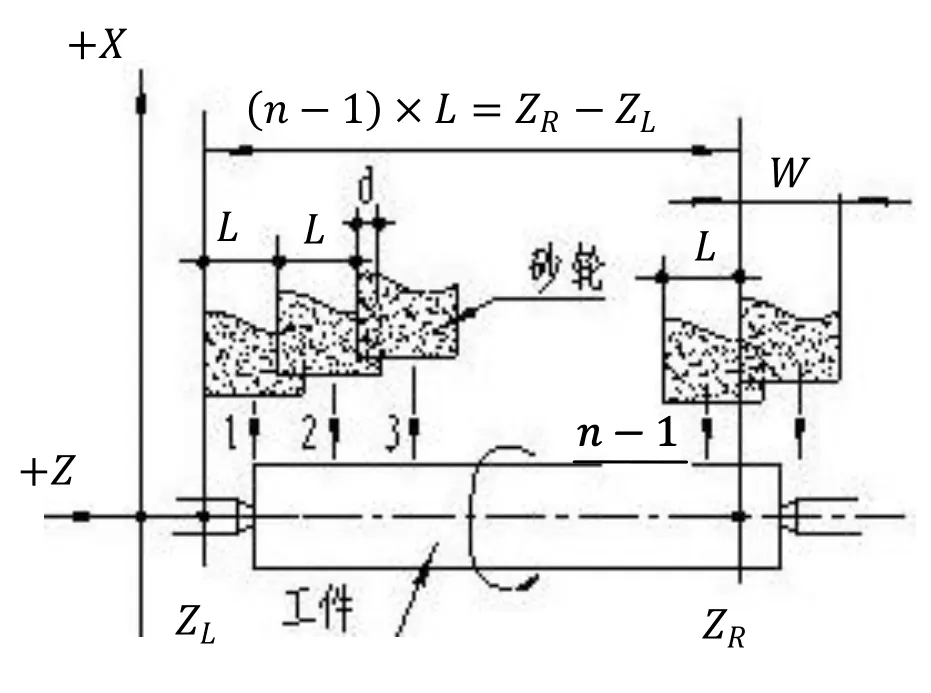
图1 磨削示意图

按磨削示意图，可得出以下公式：

将式(2)代入式（1）得：

若给定一个最小重叠量d′,(例d′=1)，根据式（3）就可计算得到n′：

当n′=int (int表示整数）

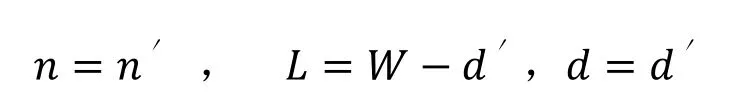
当n′≠int

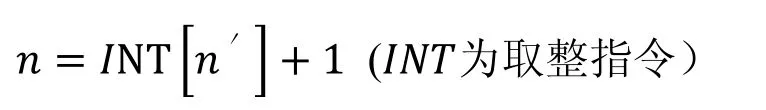
由式（2）得：d=W−L 。

由以上可知，虽然重叠量d是一个未知量，但该值越小越好，只要能满足使用即可，可以设定一个较小的值，试算出切入次数n′，若为整数，说明设定的d值刚好，可直接使用，且n为整数。若n′为非整数，就把这个n′值小数部分去掉保留整数加1作为跳档次数磨削最优，这时可依据次数n求得L，重新计算真正的d值，这个d值会比d′大一点。