全三维轴流式透平叶栅离散伴随气动优化设计
2018-09-19丰镇平
卢 娟,丰镇平
(1.中国航发中国航空发动机研究院,北京101304;2.西安交通大学能源与动力工程学院叶轮机械研究所,西安710049)
1 引言
基于控制理论的气动优化设计方法,在求解目标函数对设计变量的梯度时引入了伴随系统,又被称为伴随方法。与传统的梯度求解方法相比,伴随方法的优势在于其梯度的计算量与设计变量数目无关,计算目标函数对所有设计变量的梯度只需计算一次流场和一次伴随场,而且伴随方程是线性偏微分方程,远不及流动方程那么复杂[1]。其中,离散伴随方法因其伴随方程及边界条件的推导过程清晰规范,在更换目标函数时无需重新推导伴随系统,可获得精确的目标函数梯度值,以及伴随系统的建立过程可借助成熟的自动微分工具以便于程序开发等,自上世纪末以来得到了相关研究者的广泛关注,目前已在外流领域及部分内流领域得到了一定程度的应用[2-4]。
本文基于西安交通大学叶轮机械研究所Tur⁃boAero研究组在离散伴随气动优化设计领域已有的研究基础[5-9],在已建立的适用于二维、三维轴流式透平叶栅的离散伴随气动优化设计平台的基础上,发展了三维轴流式叶栅新型参数化方法。该方法应用NURBS技术取代原有的非均匀B样条曲线,除了对叶栅各截面型线进行拟合外,还将各截面重心及安装角纳入参数化范围。应用基于离散伴随方法的透平叶栅气动优化设计平台,对Aachen透平的第一级静叶栅在无粘、大负攻角流动条件下,以降低叶栅进出口总压损失为目标进行了气动优化设计,并研究了质量流量约束对优化效果的影响。
2 三维叶栅参数化方法
目前常用的叶栅型线参数化方法,主要基于Bezier曲线、非均匀B样条曲线及NURBS曲线三种技术实现。其中,基于Bezier曲线的参数化造型方法简单且能保证曲线高阶光滑,在各类软件中常有涉及,如文献[10]发展的BladeDesign气动设计软件就采用了基于Bezier的造型方法,但该类方法对叶栅型线的局部修改能力较差;非均匀B样条保留了Bezier曲线的高阶光滑、保凸性好的优点,同时克服了Bezi⁃er曲线不具有局部修改能力的缺点,但其不能准确表达圆弧等二次曲线;而NURBS在具备Bezier曲线及非均匀B样条的优点之外,其最突出的特点是可以精确表达二次规则曲线,其权因子的引入为曲线表示与形状控制提供了更大的便利和灵活性,使得曲线易于控制,并可实现对复杂曲线的模拟[11]。
本文将参数化方法由原先的仅对叶栅各截面型线进行非均匀B样条曲线拟合,发展为综合考虑各截面重心积叠方式、安装角转动及各截面型线采用NURBS方法进行拟合的新型参数化方法。相比于原有方法,该方法在提高拟合精度的同时,扩展了气动性能的寻优空间,为实现叶栅的全三维气动优化设计提供了保障。图1给出了重心与安装角改变带来的叶栅变化效果示意,通过控制重心的轴向坐标X可实现叶栅的倾和掠,控制重心的周向坐标Y可实现叶栅的正弯和反弯,而改变安装角可实现叶栅的扭转。
三维叶栅参数化的步骤如下:首先按优化需求将原始叶栅沿叶高生成多个截面,计算各截面的重心坐标及安装角;然后由四次NURBS曲线拟合各截面重心形成叶栅径向积叠线;在每个截面上,按照事先给定的前、尾缘长度分割因子,分别将压力面与吸力面分割成前缘段、中间段及尾缘段。为避免前、尾缘型线畸变,在设计过程中将其固定,仅对中间段型线进行参数化。通常,轴流式透平叶栅吸力面的型线曲率大于压力面,因而吸力面型线变化对叶栅性能的改变起到的作用更大。为节约计算时间,本文型线参数化仅限于叶栅吸力面。
3 气动优化设置
对Aachen透平的第一级静叶栅进行优化设计。该叶栅为环形亚声速叶栅,其基本几何和气动参数如表1所示[12]。
叶栅参数化按前述方式进行。首先将叶栅沿叶高均分为6个截面,如图2(a)所示,图中蓝色标识为截面重心。由于各截面型线参数化结果相似,本文仅给出根部截面参数化结果,如图2(b)所示。其中,用于分割吸力面的前、尾缘分割因子分别为0.08和0.85,采用四次NURBS曲线对中间段进行拟合的控制点总数为11,拟合误差小于5×10-5,满足精度要求。为保证中间段与前缘段及尾缘段的光滑连接,固定中间段前后几个点,选择第4到第9控制点为可调控制点,如图中红色实心方块所示,其横、纵坐标作为优化过程中的设计变量。
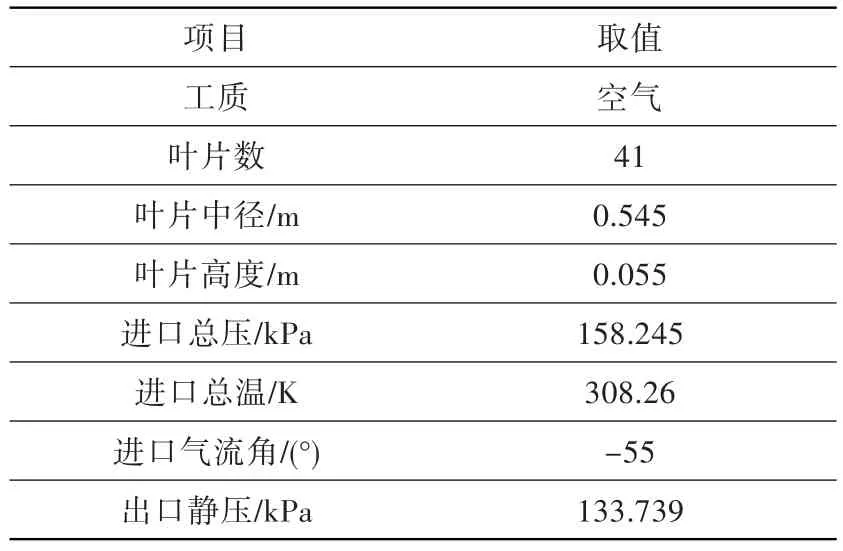
表1 三维环形叶栅几何和气动参数Table 1 Geometric and aerodynamic parameters of the 3D turbine stator cascade
三维气动优化设计在无粘环境下进行,流场数值计算的进口边界给定总温总压,进气角度与轴向成-55°夹角,出口给定静压,数值见表1。流场数值分析与伴随场计算过程中的叶栅通道计算网格采用H-O-H型拓扑结构的自生成网格,如图3所示。网格总节点数为152523。
流场求解采用基于有限体积法的可压缩流场求解器,该求解器采用了Roe格式的对流矢通量计算、中心差分格式的粘性矢通量计算、隐式源项处理及三对角隐式求解算法等数值处理方式。
三维气动优化设计的目标是使叶栅进出口总压损失系数最小。有关离散伴随方法理论、基于离散伴随方法进行叶栅气动优化设计的具体流程、总压损失目标函数的定义方式详见文献[6]、[9]。
4 优化结果分析
4.1 优化前后叶型对比
图4给出了6个截面上优化前后叶型对比,其中黑色实线为初始叶栅型线,红色虚线为优化后的叶栅型线。表2给出了各个截面上重心坐标及安装角的具体变动数值。由此可以看出,叶顶截面(Section 6)的安装角有很大程度的改变,此变化适应于流场的进口气流角,能有效减小叶顶前缘的负攻角,对流场分离具有一定的抑制作用。
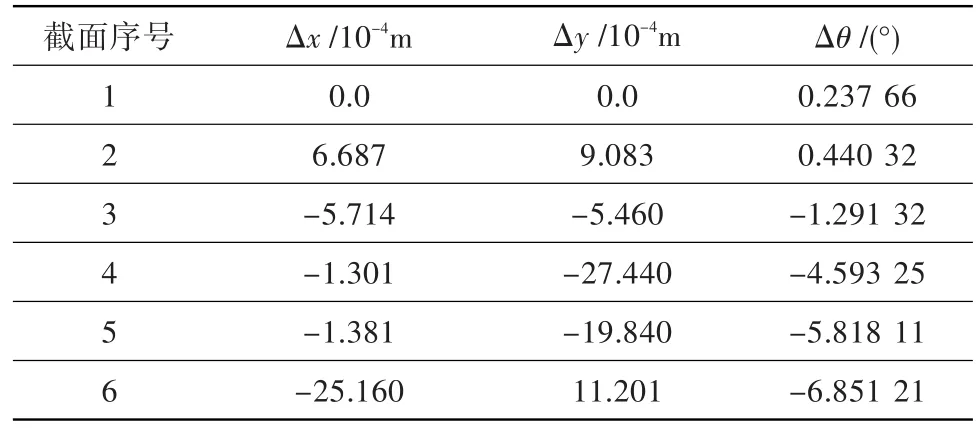
表2 优化后各截面重心与安装角的变化Table 2 The variation of centroids and stagger angles after optimization without constraint
4.2 优化前后流场分布对比
图5给出了优化前后叶栅压力面上的极限流线分布对比。由图中可看出,当进口气流角为-55°时,优化前叶栅前缘处于大负攻角状态,约20%叶高以下的流线从叶栅前缘发出后直接向下游流去,而约80%叶高范围内的流线由叶栅前缘发出后先自下而上向顶部端壁发展,一部分在发展一段时间后向下游流去,另一部分撞击顶部端壁在靠近前缘的区域形成旋涡回流,从而导致叶栅压力面处出现流动分离,尤其是中叶展以上区域最为显著。
优化后,叶栅各截面安装角及重心位置都发生了不同程度的改变,使得在进口气流角不变的情况下叶栅前缘的负攻角有了明显减小。由分析可知,叶栅中叶展以上流动分离现象显著,因此Section 4~6在优化过程中变化较大。从优化后的压力面极限流线分布可以看出,流线从叶栅前缘发出后平稳地流向下游,有效改善了通道内的流动分离情况,大大降低了流动损失。
图6给出了优化前后叶顶、75%及50%叶高截面处的流线分布对比。可见,初始叶栅在3个截面上都有不同程度的流动分离,尤其以叶顶截面最为明显。
结合压力面极限流线分布可知,在叶顶截面处,靠近前缘约15%轴向弦长处流动开始发生分离,分离区域占据了大部分流动通道;在75%叶高截面处,流动分离区域相较叶顶截面有所减小,分离起始点后移至距前缘约30%轴向弦长处;在50%叶高截面处,流动分离区域进一步缩小,分离起始位置继续后移至距前缘约40%轴向弦长处;50%叶高以下截面,未发现明显的流动分离,因此本文仅对以上3个特征截面进行分析。对比优化后叶栅在各截面的流线分布可看出,优化后叶栅各截面流动分离区域得到消除,流动情况大大改善。
图7给出了优化前后叶顶、75%及50%叶高截面处的叶片表面压力分布对比。可见,在叶顶截面处,优化前压力面靠近前缘处因流动分离较大而存在压力突跳;优化后压力突跳消除,且压力面压力有了整体提升,而吸力面压力分布后移,扩压段减小,损失降低。同时,优化后吸力面扩压段尾缘区域产生一个新的逆压梯度区域,这对叶栅气动性能有一定的不利影响,但由于该逆压区范围较小,因此叶栅在该平面上的总体性能还是得到了改善。在75%及50%叶高截面处,优化前后压力分布变化与叶顶截面处的类似,相比于初始叶栅优化后压力面压力整体都有不同程度的提升,而吸力面压力分布后移,使叶栅的后加载特性更为明显。
4.3 优化前后熵增分布对比
图8给出了优化前后叶栅压力面上的熵增分布。可见,优化前叶栅压力面前缘至约50%弦长处的区域熵值较高,尤其是中叶展以上部分处于高损失区域;而优化后整个压力面都处于低熵值区域,损失大大减小。
图9给出了优化前后不同叶高截面处叶栅通道内的熵增分布对比,可见优化后通道内高熵值区域得到有效改善。
4.4 约束对优化效果的影响
上述优化过程中未添加约束条件,虽然最后流场性能得到了很大提升,但是由于在优化过程中对叶型进行了扭转,因此质量流量发生了较大改变。为研究带与不带约束对最后优化结果的影响,对同一叶栅在相同计算条件下进行了添加质量流量约束的优化设计研究。叶栅通道内质量流量约束的定义方式见文献[6],文中目标函数与质量流量约束对应的权重系数分别取为1和10。
表3给出了各截面重心及安装角的具体变化数值。图10给出了带与不带约束优化叶栅与初始叶栅的对比。由于叶栅扭转会改变叶型的喉部面积,对通道质量流量有直接影响,因此添加质量流量约束后,各截面叶型的旋转角度都不大,只是各截面的重心位置向轴向及周向发生了不同程度的偏移。
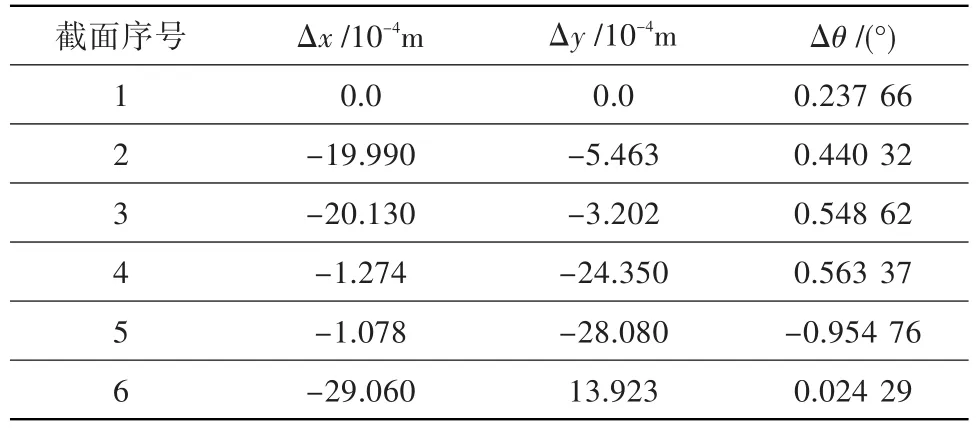
表3 带约束优化后各截面重心与安装角的变化Table 3 The variation of centroids and stagger angles after optimization with constraint
表4给出了带与不带约束叶栅优化前后的总体性能对比。可见,不带约束优化时,无量纲质量流量减少了13.91%,无量纲熵增降低了54.00%,总压系数升高了1.64%;带质量流量约束优化时,无量纲质量流量增加了1.01%,无量纲熵增降低了18.76%,总压系数升高了0.568%。
由以上的数据对比及分析可知,不带质量流量约束时,优化后叶栅通道内的流动状态及叶栅气动性能,相较原始叶栅及带约束优化后的叶栅都有较大的改善或提高,然而叶栅通道内质量流量也随之下降较多,因此无约束优化叶栅气动性能的提升是以降低叶栅通流能力为代价。带质量流量约束时,虽然叶栅的通流能力变化大不,但是叶栅气动性能的提高及流动状态的改善十分有限,对于本文中由于进口大负攻角导致的流动分离现象不能有效解决。实际应用中,应根据需要选择是否添加流量约束及约束权重系数大小来进行具体的设计优化。
5 结论
发展了适用于轴流式透平叶栅的全三维叶栅参数化方法。该方法采用NURBS技术,提高了叶型拟合精度,同时将叶栅型线、重心及安装角全部纳入参数化范围,加大了设计变量的自由度,扩展了叶栅性能的优化空间。基于该方法,应用前期开发的离散伴随气动优化设计平台,对Aachen透平第一级静叶栅在无粘、大负攻角流动条件下,以降低叶栅进出口总压损失为目标进行了优化设计。设计结果表明,优化后的三维叶栅形状明显改变以适应来流攻角变化,通道内流动得到良好改善,气动性能明显提高,由此验证了本文发展的新型叶栅参数化方法用于叶栅全三维气动优化设计的有效性。此外,约束条件对优化效果有较大影响,实际应用中应根据需要进行具体的优化设置。尽管无约束优化很难用于实际,但其可为叶栅性能改善机理研究提供指导依据。
