转速对小展弦比压气机叶片静气动弹性的影响

2018-09-19汪松柏黄大全李春松

燃气涡轮试验与研究 2018年4期

汪松柏，黄大全，李春松

(1.中国航发四川燃气涡轮研究院，成都610500；2.中国人民解放军5719厂，成都611937)

1 引言

为实现涡扇发动机高推重比需求，跨声速压气机叶片具有高级负荷、高叶尖切线速度、高级压比、小展弦比和弯掠叶型等设计特点[1-2]，这使得跨声速转子叶片在高气动力和离心力共同作用下的静气动弹性变形问题越来越突出。随着级负荷的进一步提高，叶型几何形状细微差别都将使得压气机工作偏离理想设计工况，非设计工况甚至引起叶片的结构强度和疲劳寿命问题。因此，研究小展弦比压气机叶片不同工作转速下的静气动弹性问题，对于高性能涡扇发动机压气机设计十分重要。

压气机叶片工作过程中因承受气动力、离心力和非均匀温度载荷，导致叶片产生一定的静气动弹性变形，从而影响叶片气动性能。国内外学者对此开展了大量的研究工作。Mahajan等[3]分析了GE公司E3发动机大涵道比凸肩风扇叶片在气动力、离心力和非均匀温度载荷共同作用下的静气动弹性变形，发现温度载荷对风扇叶片静气动弹性变形的影响不大。Roehle等[4]的实验表明，叶型几何细微变化对压气机吸力面上激波位置有重要影响。杨慧等[5]研究了叶片反扭对跨声速大涵道比风扇气动性能的影响，指出叶片反扭变形对流量的影响会使得发动机起飞推力小于预测值。郑赟等[6-7]发展了适合叶轮机风扇叶片反扭设计的流固耦合计算方法，对风扇叶片从设计热态叶型到冷态加工叶型进行了反推计算，获得了更为精确的制造叶型。李彬等[8]考虑流固耦合对涡轮长叶片气动和强度性能的影响，发现叶片变形会改变表面气动载荷分布和出口气流角。

现代高性能弯掠叶片积叠规律复杂使得叶片变形规律特殊，同时静气动弹性变形受压气机具体工作状态和叶片变形规律的影响。为研究转速对静气动弹性的影响，本文采用双向瞬态的流固耦合数值方法，对某1.5级小展弦比跨声速压气机转子叶片在不同转速下的静气动弹性变形过程进行模拟。通过固体域和流体域连续区域的离散化和构造插值函数求解各自的动力学方程，在流固耦合交界面上实现物理量的传递以模拟气流和叶片非线性耦合作用过程。重点分析了不同转速下叶片在气动力和离心力共同作用下的静气动弹性变形规律及其对气动性能的影响。

2 研究对象与数值方法

2.1 研究对象

以1.5级小展弦比跨声速压气机为研究对象，计算几何模型由进口导叶、转子叶片以及静叶组成。主要设计参数为：转子叶尖切线速度约450 m/s，进口导叶稠度1.17，转子叶片稠度1.50，展弦比约1，动叶叶尖和导叶叶根间隙均为0.45 mm。

2.2 数值研究方法

流场计算模型和固体域有限元模型如图1所示，叶栅通道空间网格离散采用IGG/AutoGrid5模块生成。整个模型采用H-O型结构化网格，其中进、出口延伸段均为H型网格，叶片通道为O型结构化网格，近壁面第一层网格为1×10-5m，无量纲参数Y+值在10～20之间，网格总节点数约80万。转子叶片有限元模型采用六面体结构化网格，总节点数约为3000。

转子叶片在离心力和气动力共同作用下的静气动弹性变形，是一个典型的双向流固耦合问题。流场气动力加载到叶片表面引起叶片产生静气动弹性变形，叶片变形后作为边界条件会改变周围流场，同时流场变化后压力分布又影响叶型几何。本文采用双向瞬态的流固耦合数值方法，分别用有限体积法计算流场和有限元法计算结构场。流体域和固体域采用内外循环迭代求解的方法，其耦合求解过程如图2所示。外循环控制流固耦合计算非定常时间步，内循环控制流体域和固体域交界面上的插值和数据传递。当内循环流体域和结构域的载荷和位移都达到收敛状态时迭代结束，进入下一个时间步的外循环，整个时间推进过程中求解动网格上的N-S方程。

流固耦合交界面上，流体网格和固体网格很难一一对应。本文利用ANSYS多物理场求解器(MFX)定义耦合边界，采用守恒插值法在交界面上实现气动载荷和结构边界位移等信息数据传递。网格变形采用多块网格变形技术，远离叶片边界网格保持不动，叶片变形通过指数衰减的方式传递到各块边界上，网格较密和变形较大的区域增加网格刚度，以保证叶片变形后的网格质量较高，避免因网格变形过大出现负体积导致计算终止。流固耦合计算过程中，为使结构以最短时间达到静气动弹性变形的平衡位置，假设结构的阻尼低于临界阻尼，其具体方法和操作过程参见文献[9]和[10]。

流体域计算的边界条件如下：导叶进口总温288.15 K、总压101325 Pa，来流速度平行于轴向，出口条件为径向压力平衡，湍流度5%。轮毂和机匣给定绝热光滑壁面，计算过程中未考虑转静叶之间的非定常干涉，转静交界面采用周向平均的混合平面法。流固耦合计算过程中，压气机单通道旋转周期为1×10-4s，将每单个通道周期分为20个时间步，非定常物理时间步长为5×10-6s，为保证流固耦合计算结果收敛，每个子步内流体和结构耦合迭代10次。湍流计算选取k-ε两方程湍流模型，对近壁面边界层流动使用Scalable壁面函数处理。

3 计算结果分析

3.1 不同转速下的气动性能

图3给出了叶片在气动力和离心力共同作用下，60%、80%、100%转速时热态和冷态叶型气动特性对比。图中，虚线为冷态叶型气动特性，实线为气动力和离心力共同作用下双向流固耦合计算的热态叶型结果。可看出，同一转速下，叶片静气动弹性变形后的特性线均向右发生一定偏移，80%和100%转速下偏离效果显著。从最大流量看，叶片静气动弹性变形后，三个转速下对应的堵塞流量增加了0.455%～0.913%，其中80%转速下增加比例最大。这是由于叶片在离心力作用下出现扭转恢复现象，使得叶栅通道的流通面积增大，流通能力增强。从最大效率参数看，80%转速下最大绝热效率相对冷态叶型增加了1.10%，60%和100%转速下最大绝热效率分别增加了0.39%和0.11%。同时，叶片静气动弹性变形后，近失速工况的总压比均出现一定程度的增大。

3.2 不同转速下的叶片变形规律

时域双向流固耦合计算中，由于流体和固体网格一般在交界面上不能完全重合，所以流固间的双向插值精度将直接影响计算精度。图4为流固耦合交界面上静气动弹性变形量参数插值前后对比。从变形量参数分布规律和吻合度看，采用的插值方法精度高，插值效果好。

压气机设计工作点一般在高效率点附近，对于不同转速，本文均针对最大效率点工况进行分析。图5为不同转速最高效率点工况叶片在气动力和离心力共同作用下的整体静气动弹性变形规律。由图可看出，叶片静气动弹性变形量随叶高逐渐增大，最大变形量均出现在叶尖前缘。从流向看，前缘变形量最大，尾缘次之，中间弦长变形量最小。不同转速下小展弦比转子叶片的静气动弹性变形规律均以扭转变形为主导。

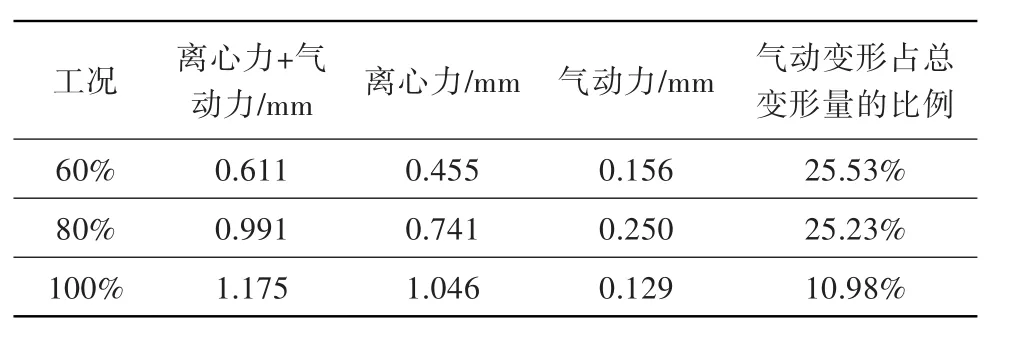
表1 不同转速最大效率点工况下叶片静气动弹性变形最大值Table 1 The maximum static deflection under different conditions

表1为不同转速最大效率点工况叶片静气动弹性变形量最大值。从表中可看出，叶片的静气动弹性变形量主要由离心力贡献，气动力引起的变形量占总变形量的比例在非设计转速工况远远大于设计转速工况。

表2为不同转速气动力和离心力共同作用下叶片各变形分量幅值变化。从表中可看出，不同转速下叶片静气动弹性变形分量中，以轴向变形分量最大，其次为周向，径向变形分量最小。叶片在载荷作用下沿叶高方向产生复杂的三维几何变形，使得叶片的几何进气角、出气角、叶尖间隙等参数发生改变，进而影响压气机的气动性能。图6为不同转速下叶尖径向变形位移沿流向的变化规律。由于小展弦比叶片在载荷作用下以扭转变形为主导，前缘和尾缘的径向变形位移相对较大，70%左右弦长位置的变形最小，使得叶尖形成不规则的微凹形截面，影响叶尖间隙泄漏和二次流动。

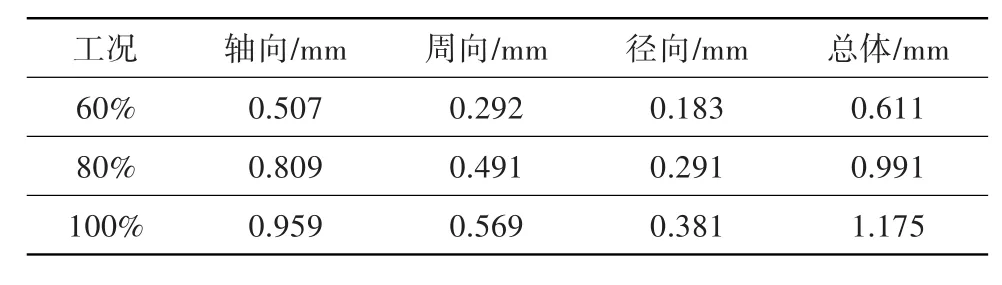
表2 气动力和离心力共同作用下各方向变形量幅值Table 2 Deflection amplitude under aerodynamic and centrifugal loads

3.3 不同转速下的转子表面静压分布

图7为不同转速下叶片静气动弹性变形前后90%叶高截面的静压对比。图中Steady computation为不考虑叶片变形(冷态)的定常计算结果，Static deflection为叶片在气动力和离心力共同作用变形后(热态)的计算结果。从图中可看出，100%和80%转速下，转子吸力面存在较强激波。叶片静气动弹性变形后明显使得激波位置前移、强度增强，80%转速下激波位置的变化较100%转速下更加明显，对气动性能的影响更大。60%转速下压气机处于亚声速流动，通道没有激波产生，静气动弹性变形对叶片表面静压分布影响相对较小。综合上述三个工况，叶片静气动弹性变形主要影响通道的激波位置和强度，从而使得气动性能发生较大改变。

3.4 不同转速下的转子激波对比

图8为不同转速下转子叶片静气动弹性变形前后80%叶高截面的相对马赫数云图。从图中可看出，80%和100%转速下转子通道存在明显的激波，且静气动弹性变形后的通道激波的强度更强。叶片在气动力和离心力共同作用下出现扭转恢复，相同来流条件下静气动弹性变形导致转子进口攻角增加，通道激波强度增强。60%转速下转子通道不存在激波，与图7中的表面静压分布情况一致。