基于行波传播路径的不等长双回线路单端行波测距
2018-09-18束洪春田鑫萃
束洪春, 宋 晶, 田鑫萃
(昆明理工大学电力工程学院, 云南省昆明市 650051)
0 引言
单端行波测距能否实现自动化的关键是故障点反射波的可靠检测、有效表征、准确甄别以及精确标定[1-5]。文献[1]提出利用初始行波与第2个反向行波得到的初步距离建立特征波对,根据特征波对之间的极性关系可以识别第 2 个反向行波的来源。文献[2]提出采用双端法实现故障点反射波与对端母线反射波的辨识。文献[3]提出了利用行波信号的 Lipschitz指数将行波信号的时频特性联系起来,运用最小二乘法拟合检测到的第2个行波波头的Lipschitz指数,并据此确定故障行波的频率成分及其到达时刻,计算故障距离。文献[4]推导出二次侧行波波头衰减振荡的数学表达式,并通过数值计算的方法给出衰减振荡频率与二次侧传输电缆长度的关系,并基于此,提出利用二进小波变换、Prony分解以及单端工频阻抗算法结合的单端组合测距方法;文献[5]通过引入电压行波,构造“综合行波极性”剔除母线两端的健全线路末端反射波。这些方法大多是基于仿真数据进行研究,而对实测数据的研究甚少。由行波网格图的行波表征体系可知,故障点反射波可看作是初始行波经过一段时间的延时。因此,故障点反射波与初始行波具有一定的相似性。当故障点反射波与故障初始行波具有很高的相似性(斜率和幅值)时,则故障点反射波易于辨识。当故障点反射波与故障初始行波相似度减小时,则故障点反射波不易辨识。通过对实测行波数据进行分析发现,雷击闪络故障电流行波的初始行波的幅值很大,而故障点反射波的幅值较故障初始行波的幅值小很多,且雷击闪络故障往往是金属性故障,对端母线反射波的幅值也较小[6-8]。当故障初始行波与故障点反射波(对端母线反射波)相差较大时,在同一坐标轴上,无论是从机器视角还是人眼视角,故障点反射波都难辨识出。因此,对于雷击引起的闪络故障行波采用传统的故障点反射波辨识方法,不易识别出[9-11]。对于双回线路行波测距,惯常采用相模变换得到单一模量后[12],使用单回线路行波测距算法实现故障定位,但该方法不适用于局部耦合不等长的双回线路,而在现场实际中,80%以上的输电线路都不是完全等长的,而对于不等长的双回线路的故障测距算法研究甚少[13]。同时,这样的测距算法,往往忽略了双回线路故障行波传播的特点。文献[14]提出了采用基于回路电流故障主导波头到达时差的输电线路故障测距,该方法采用观测端的故障线路和健全线路各自检测到一次属于它自己电流互感器(TA)所观测的故障初始行波进行故障测距,但该方法未讨论其最适合应用的场景以及是否适用于不等长双回线路。
本文分析了不等长双回线路单回线路发生单相接地故障时,故障行波在双回线路中的传播路径,并得到故障回线和健全回线量测端两个坐标轴上观测到的行波波头在时间轴上的分布特点,基于此提出了采用故障线路量测端和非故障线路量测端两个尺度上辨识出属于自己TA所观测的故障初始行波到达时刻,实现了不等长双回线路故障测距。基于行波传播路径的单端行波新方法相比较传统单端行波测距,它利用两个量测端观测到的行波分布特点,易于确定故障行波的性质,且于健全线路量测端观测,故障初始行波与含有故障信息的故障行波(以下简称健全回线初始行波),其幅值和斜率,相差较小,能够可靠地检测、标定和辨识出,特别适用于雷击闪络故障引起的电流行波,且健全回线初始行波不受过渡电阻折反射的影响;与传统的双端行波测距比较,它无须双端通信。
1 利用单侧信息的不等长双回线路行波测距
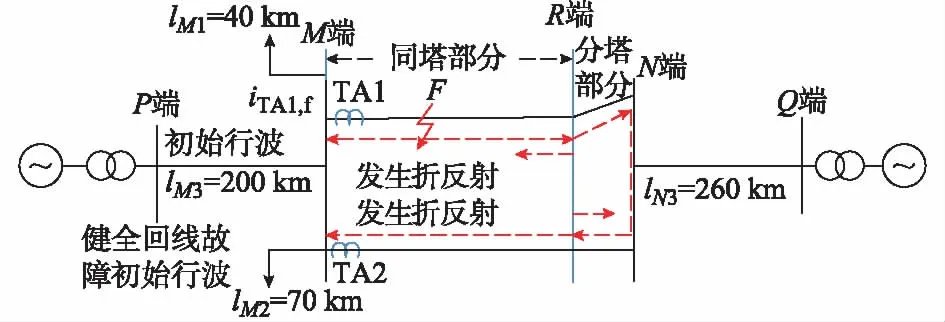
现将不等长双回线路拆开成如图1所示的结构。由图1可知,双回线路一回线路故障,一方面,起始故障行波由故障点经故障回线传播至量测端;另一方面,故障行波由故障点经健全回线传播至量测端。由文献[12]可知,可将起始故障行波由故障点经故障回线传播至量测端对应TA视为“首端”,并称该行波为故障回线初始行波;将起始故障行波由故障点经健全回线传播至量测端对应的TA视为“末端”,并称该行波为健全回线初始行波,双回线路“l1+l2”视为“被检测线路”。
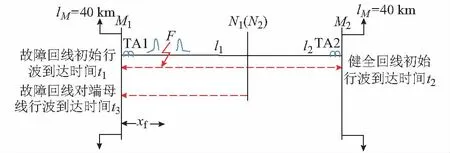
图1 不等长双回线路测距示意图Fig.1 Schematic diagram of fault location for unequal-length double-circuit lines
根据图1和双端测距公式,得到故障点距离“首端”的距离xf为:
(1)
式中:xf为离开“首端”的距离;t1为故障初始行波到达“首端”TA的时刻;t2为健全回线初始行波到达“末端”TA的时刻。
由式(1)可知,若能辨识出故障回线初始行波和健全回线初始行波,就能采用式(1)进行故障测距。
2 由同侧TA1和TA2观测到的行波(群)分析与辨识
由文献[14]可知:①对于等长双回线路,若健全回线量测端检测到的电流行波是故障回线故障行波的透射波,则其小波变换模极大值小于故障回线的故障行波小波变换模极大值,且两者极性相反;②若TA1和TA2量测端检测到的行波为量测端其他健全回线末端反射波,则两者的极性相同,且幅值相等;③若健全回线量测端检测到健全回线故障初始行波,则它与故障回线初始行波同极性。基于此,可以辨识出健全回线初始行波。而对于不等长双回线路,于TA1和TA2量测端观测,故障回线对端母线反射波与健全回路故障初始行波不是同时刻到达量测端,分塔处阻抗不连续点引起的反射波也会到达量测端,因此对于不等长双回线路,需要分析其是否影响健全回线初始行波的辨识。
现分别讨论故障回线长度lF小于健全回线长度lnF以及故障回线长度lF大于长度lnF时,在量测端TA1和TA2观测到的行波群的性质。
1)故障回线长度lF小于非故障回线长度lnF
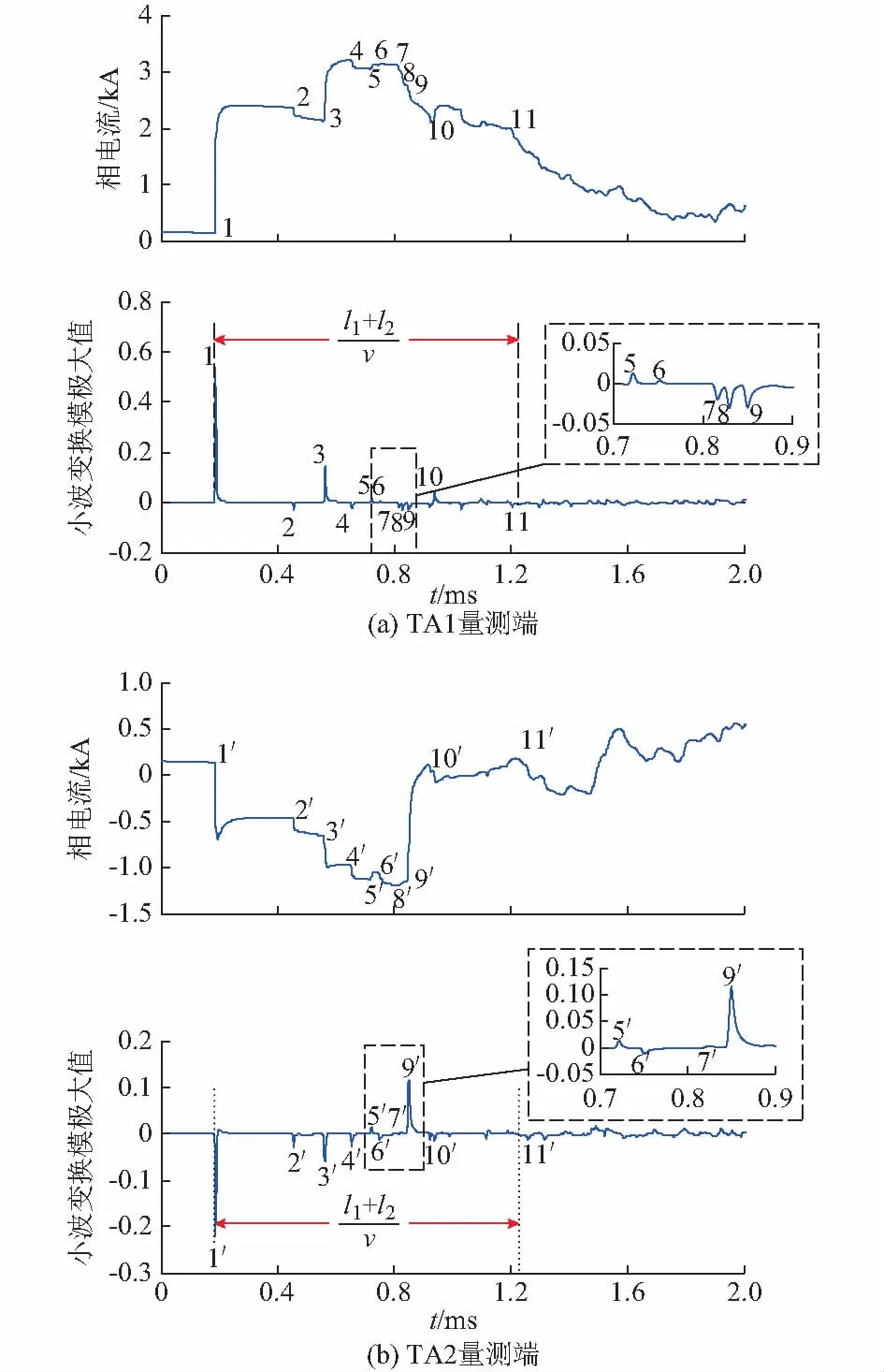
不等长双回线路结构如图2所示,其中l1=150 km,l2=160 km,l1 图2 不等长双回线路(l1 由图2可知,TA1检测到的故障初始电流行波为: (2) 式中:uf为故障点处的电压行波;Zc和γ分别为Ⅰ回线或Ⅱ回线对地的波阻抗和传播常数;xf为距离故障回线TA的距离;βM为M端反射系数。 故障初始电流行波经M端透射至Ⅱ回线路,量测端TA2检测到的故障初始行波为: (3) 式中:αM为M端折射系数。 由式(1)和式(2)可知,TA1检测到的故障初始行波幅值与TA2检测到的故障初始行波的透射波之比满足: (4) M端反射系数βM和折射系数αM与出线的关系分别为βM=(nM-1)/(nM+1),αM=2/(nM+1),其中nM为M端出线数。 由式(3)可知,当nM>1,表明只要量测端母线除故障线外的出线数大于1,则故障初始行波的幅值大于其透射波的幅值。对于双回线路,均满足式(3)。基于此,可以判别出故障回线。 当lF (5) 式中:βR为Ⅰ回线中阻抗不连续处的反射系数,且βR=(Zc,RN-Zc,MR)/(Zc,RN+Zc,MR);αF=2Rf/(Zc+2Rf),为故障点反射波系数。 由式(5)可知,若上游线路MR的波阻抗Zc,MR小于下游线路RN波阻抗Zc,RN,则于故障回线量测端TA1观测到的极性与故障初始行波反极性;反之,则与故障初始行波同极性。 同时,故障回线对端母线反射波也先于健全回线初始行波到达量测端。 (6) 式中:βN为N端反射系数。 同时,故障行波由故障点传播至N端,再经健全回线传播至TA2,TA2量测端检测到的故障初始行波为: (7) 式中:αN为N端折射系数且αN=2/(nN+1),其中nN为N端出线数。 由式(7)可知,健全回线初始行波不受故障点过渡电阻的影响。由式(5)和式(6)可知,若忽略故障行波在线路中传播的损耗,TA1检测到的iTA1,R的幅值与故障回线对端母线反射波幅值之比为: (8) 由式(8)可知,iTA1,R的幅值取决于R处的不连续程度,iTA1,N的幅值取决于N端母线的出线数目。 同理,由式(6)和式(7)可知,若忽略故障行波在线路中传播的损耗,TA1检测到的对端母线反射波iTA1,N与健全回线故障初始行波iTA2,f同极性且幅值满足: (9) 综上分析可知,过渡电阻阻值越大,N端出线越多,则故障回线对端反射波iTA1,N的幅值越大。若线路发生金属性故障,αF≈0,故障回线对端母线反射波幅值较小。可见,当线路发生雷击闪络故障时,接地电阻阻值很小,故故障回线对端母线反射波的幅值很小,不易辨识。 由式(3)和式(7)可知,TA2检测到的透射波与TA2检测到的故障初始行波反极性,若忽略故障行波在线路上的传播损耗,其幅值之比为: (10) 由式(10)可知,iTA2,r和iTA2,f的幅值之比大小与M端和N端的母线接线形式的关系如附录A表A1所示。由表A1可知,至少有2/3概率故障初始行波的透射波幅值小于健全回线故障初始行波幅值,而只有当N端母线和M端母线的出线数满足nN+1>2nM时,即N端的出线数目要大于2倍的M端母线出线数目,故障初始行波的透射波幅值才大于健全回线初始行波,但是这样的接线方式在220 kV以上的输电网并不常见。可见,一般情况下故障初始行波的透射波幅值小于健全回线初始行波。因此,于健全回线量测端,以故障初始行波的透射波为基准,健全回线故障初始行波易于辨识。 现假设Ⅰ回线路距离M端56 km发生A相接地故障,过渡电阻为10 Ω,故障初相角为90°,M量测端TA1和TA2的故障相电流行波及其对应的小波变换模极大值如图3所示。在图3(a)中,故障回线量测端观测到的行波1为故障回线初始行波,2为健全线路lM1末端反射波,3为故障点反射波,4为健全线路lM2末端反射波,5为健全线路lM1末端第二次反射波,6为分塔处阻抗不连续点反射波的透射波,7为故障回线N端反射波,8为反映xf+lM1的健全线路末端反射波,9为健全回线初始行波的透射波,10为故障点第二次反射波,11为反映l1+l2长度的N端反射波。在图3(b)中,健全回线量测端观测到的行波1′为故障初始行波的透射波,2′为健全线路lM1末端反射波,3′为故障点反射波的透射波,4′为健全线路lM2末端反射波,5′为健全线路lM1末端第二次反射波,6′为分塔处阻抗不连续点的反射波,7′为Ⅰ回线N端反射波的透射波,8′为反映xf+lM1的健全线路末端反射波,9′为健全回线初始行波,10′为故障点第二次反射波的透射波,11′为反映l1+l2长度的N端反射波。 图3 不等长双回线(l1 由上述分析,当故障回线长度lF小于非故障回线长度lnF,于故障回线TA1量测端,分塔处阻抗不连续点的反射波的透射波(6)、故障回线N端反射波(7)会先于健全回线初始行波透射波(9)到达量测量测端TA1;于健全回线TA2量测端,分塔处阻抗不连续点的反射波(6′)、故障回线N端反射波的透射波(7′)也会先于健全回线初始行波(9′)到达量测端TA1,但是分塔处阻抗不连续点的反射波和故障回线N端反射波的幅值很小,不会影响检测与辨识。 2)故障回线长度lF大于非故障回线长度lnf 不等长双回线路结构如图4所示,其中l1=160 km,l2=150 km,l1>l2。若假设Ⅰ回线路于F点发生单相接地故障,故障行波在双回线路中的传播路径如图4中虚线所示。 图4 不等长双回线路(l1>l2)Ⅰ回线路发生故障下故障电流行波的传播路径Fig.4 Propagation path of fault current traveling wave under circuit Ⅰ fault of unequal-length double-circuit lines (l1>l2) 由图4可知,当lF>lnF,从理论上来说,于故障回线TA1检测到分塔处阻抗不连续点反射波iR先于健全回线故障初始行波到达量测端,而对端母线反射波会滞后于健全回线故障初始行波到达量测端,因此对端母线反射波不会影响健全回线初始行波的辨识。现假设Ⅰ回线路距离M端56 km发生单相接地故障,过渡电阻为10 Ω,故障初相角为90°,M量测端TA1和TA2的故障相电流行波及其对应的小波变换模极大值如图5所示。在图5(a)中,故障回线量测端观测到的行波1为故障回线初始行波,2为健全线路lM1末端反射波,3为故障点反射波,4为健全线路lM2末端反射波,5为健全线路lM1末端第二次反射波,6为分塔处阻抗不连续点的反射波,7为Ⅱ回线N端反射波的透射波,8为反映xf+lM1的健全线路末端反射波,9为健全回线初始行波的透射波,10为Ⅰ回线N端反射波,11为故障点第二次反射波,12为反映l1+l2长度的N端反射波。在图5(b)中,健全回线量测端观测到的行波1′为故障初始行波的透射波,2′为健全线路lM1末端反射波,3′为故障点反射波的透射波,4′为健全线路lM2末端反射波,5′健全线路lM1末端第二次反射波,6′为分塔处阻抗不连续点的反射波,7′为Ⅰ回线N端反射波的透射波,8′为反映xf+lM1的健全线路末端反射波,9′为健全回线初始行波,10′为故障点第二次反射波的透射波,11′为反映l1+l2长度的N端反射波。 通过上述仿真分析可知,当故障回线长度lF大于非故障回线长度lnF,于故障回线TA1量测端,分塔处阻抗不连续点的反射波的透射波(6)、健全回线N端反射波(7)会先于健全回线初始行波透射波 (9)到达量测量测端TA1;于健全回线TA2量测端,分塔处阻抗不连续点的反射波(6′)、健全回线N端反射波的透射波(7′)会先于健全回线初始行波(9′)到达量测端TA1,但是分塔处阻抗不连续点的反射波和健全回线N端反射波的幅值很小,不会影响检测与辨识。 图5 不等长双回线路(l1>l2)Ⅰ回线路发生故障下M量测端故障电流行波及其小波变换模极大值Fig.5 Fault current traveling wave and wavelet transform modulus maxima of M measurement terminal under circuit Ⅰ fault of unequal-length double-circuit lines (l1>l2) 由上述分析可知,对于不等长双回线路单回线路发生单相接地故障,由量测端观测到的分塔处阻抗不连续点的反射波幅值较小不会影响健全回线故障初始行波的辨识,而故障回线对端母线反射波是否影响健全回线初始行波的辨识与故障点过渡电阻有关。附录A表A2梳理了基于行波传播路径的新单端行波测距与传统单端行波测距和双端行波测距所需辨识的行波波头的表达式。由表A2可以得到以下结论。 1)新单端行波测距和传统双端行波测距所需的行波波头与故障点过渡电阻的折反射无关,而传统单端行波与故障点过渡电阻的折反射有关,且故障点过渡电阻越大,对端母线反射波幅值越大而故障点反射波幅值越小。 2)对于等长双回线路,故障回线对端母线反射波与健全回线初始行波同时刻到达量测端。可见,若传统单端行波测距采用故障点反射波进行测距,则半线长内故障,线长引起的行波衰减程度小于新单端行波测距。而半线长外故障,线长引起的行波衰减程度大于新单端行波测距。因此,在传统单端行波测距可以测距的线长范围,新单端行波测距均可可靠测距。 3)对于雷击闪络故障,故障点往往是金属性接地,因此对端母线反射波的幅值很小,同时雷击闪络引起的电流行波中含有的雷电流高频分量沿线路传播中衰减最快,因此于故障回线量测端,故障初始行波远大于故障点反射波,以故障初始行波为基准,不易辨识。 4)传统双端行波测距两端需要同步,新单端行波测距不要两端同步。 为了进一步比较三种行波测距,提取出了各个指标,具体情况如附录A表A3所示。由表A3可知,新单端行波测距性能优于传统单端行波测距,稍弱于传统双端行波测距,可作为双端行波测距的一种补充,特别适合于只有一端装有行波测距或是两端存在同步误差的场景。 由上述分析可知,无论双回线路是否等长,当双回线路中的单回线路发生接地故障,于双回线路的TA1和 TA2量测端均能检测到来自故障点的初始行波,故采用式(1)可以实现双回线路故障测距,算法关键步骤如下。 步骤1:读取由TA1和TA2所获取的故障行波数据,并采用3次样条小波函数对TA1和TA2所获取的电流行波进行检测和标定。 步骤2:根据步骤1比较TA1和TA2的首个行波的小波变换模极大值,较大值对应的TA所在的回线为故障回线,据此实现故障回线的判断。同时,截取[t0,t0+(l1+l2)/v]时窗长内电流行波小波变换模极大值的检测和标定结果,形成健全回线和故障回线的时刻—幅值极性矩阵分别为: (11) (12) 步骤3:根据故障回线的时刻—幅值极性矩阵MF确定MF1为故障回线初始行波。 步骤4:以Mn为基准,若存在|tnp-tFp|≤4 μs(p=2,3,…,j;q=2,3,…,k)且Mnp-MFq≈0,则判断Mnp和Mnq为健全线路末端反射波;若|tnp-tFp|≤4 μs,且|Mnp|>|MFq|,Mnp/MF1>0,则Mj为健全回线初始行波。 步骤5:根据步骤3得到故障回线初始行波到达时刻为tF1;根据步骤4得到健全回线初始行波到达时刻为tnp,则可以根据式(1)得到故障距离。 步骤6:若p=2,3,…,j,q=2,3,…,k,均不满足|tnp-tFq|≤4 μs,且Mnp/Mn1<0,则Mnp可能为健全回线初始行波,根据式(1)得到可能的故障距离。 对于单端行波测距,只有正确辨识出故障点反射和对端母线反射波,才能保证测距结果是可靠的。上述测距算法采用两个量测端观测到的故障行波的时刻、幅值和极性来保证测距的可靠性,但是对于现场实测数据,往往很难保证故障行波的时刻、幅值和极性均满足步骤3和步骤4,针对此情况,若满足步骤6,从理论上说,得到一个可能的故障距离。因此,需要借助更多信息进行进一步判断[15],这是作者后续研究的内容。 2013年9月21日01:32:07,某220 kV电网大(理)—苏(屯)Ⅱ回线路A相遭受雷击,发生闪络故障,大苏线接线如附录A图A10所示。于苏屯站TA1和TA2量测端获取到的时域波形如附录A图A2所示,对应的小波变换模极大值如附录A图A3所示。所有算例中采样频率为1 MHz。 采用实测数据和式(1)计算得到的故障测距结果如表1所示。 表1 采用实测数据得到的测距结果Table 1 Fault location results obtained by using measured data 本文针对不等长双回线路,提出了采用同一观测端的故障线路和健全线路各自检测到一次属于它自己TA所观测的故障初始行波的双端原理单侧数据的故障定位方法,大量实测数据表明该测距方法具有以下特点。 1)采用同侧故障线路量测端和非故障线路量测端联合观测和辨识故障行波,可以可靠地辨识出故障行波的性质,提高单端测距的可靠性。 2)该测距方法能够实现不等长双回线路的可靠和精确测距,且无须双端通信。 3)对于现场实测数据,往往很难保证故障行波的时刻、幅值和极性均满足本文所提的方法。如何借助更多信息,进一步确定故障位置是后续继续研究的内容。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 束洪春(1961—),男,教授,博士生导师,主要研究方向:电力系统新型继电保护与故障测距、故障录波、数字信号处理及应用等。E-mail: kmshc@sina.com 宋 晶(1979—),女,博士研究生,主要研究方向:新型继电保护与故障测距。E-mail: 8680622@qq.com 田鑫萃(1986—),女,通信作者,博士,讲师,主要研究方向:新型继电保护与故障测距、高压直流线路控制与保护。E-mail: 1105479731@qq.com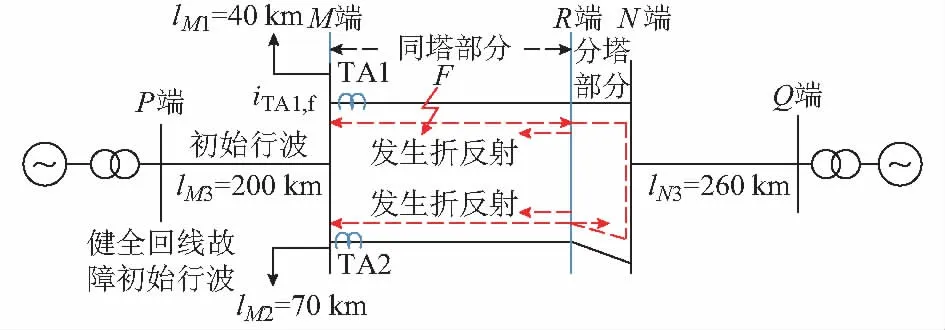
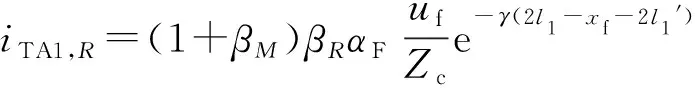
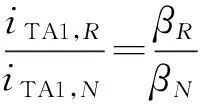

3 新单端行波测距与传统单端行波测距和双端行波测距比较
4 测距实例验证
4.1 测距算法主要步骤
4.2 实例分析及验证


5 结语
