基于自适应虚拟阻抗的虚拟同步机功率解耦控制策略

屈子森, 蔡云旖, 杨 欢, 董宁波, 赵荣祥, 韩俊飞

(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 内蒙古电力(集团)有限责任公司内蒙古电力科学研究院, 内蒙古自治区呼和浩特市 010020)

0 引言

全球能源紧缺及环境问题愈发严重,因此光伏、风能等可再生能源得到广泛的研究与发展[1-2]。然而,随着分布式能源渗透率的日趋上升,电力系统中同步发电机的装机比例相对下降,更为严重的是大量电力电子变流器的使用使得电力系统缺少足够的惯性和阻尼,系统的稳定性受到挑战,由此,虚拟同步机(VSG)技术应运而生[3-5]。

分布式电源的控制当中,用以模拟电网中同步发电机P-f和Q-U特性曲线的下垂控制策略最为常见[6],但下垂控制策略没有考虑发电机转子所具有的惯量特征,暂态响应速度过快,不能为维持电网稳定提供足够的保障[7]。VSG的核心是通过模拟同步电机转子方程为系统提供惯量及阻尼支撑,并辅以无功功率—电压控制,从而使得分布式电源具有良好的频率、电压支撑与调节作用[8-9]。所以从分布式电源友好特性的角度来讲,微网中以VSG控制替代下垂控制更具优势,众多专家学者也做出了诸多相关研究[10-12]。但无论是VSG控制技术还是下垂控制技术都会遇到功率耦合问题,通常在分析过程中会假设变流器输出电压至并网点电压之间的输电线路的等效阻抗为纯感性[13]或纯阻性[14]。然而在实际当中,输电线路,尤其是低压线路,呈现出阻感特性,从而引起了有功功率与无功功率的耦合,影响了控制性能[15]。

为实现分布式电源有功功率和无功功率的解耦控制,文献[16]通过引入与线路阻抗相关的变换矩阵,提出虚拟功率控制策略,其本质是控制回路功率耦合的消除,而实际的有功功率和无功功率仍然存在耦合。文献[17-18]控制核心思想来源于虚拟功率控制,凭借变换矩阵引入了虚拟频率与虚拟电压以实现功率解耦。文献[19]凭借相对增益矩阵深入分析了功率耦合机理,并提出了基于目标函数对角化解耦的控制方法。功率解耦控制的另一种主流方法是虚拟阻抗技术,通过虚拟电感[20]、虚拟电阻[21]、虚拟负阻抗[22]等方式改变系统阻抗的阻感比例,达到解耦的目的;进一步,诸多研究还针对虚拟阻抗技术带来的电压降等不利影响展开深入研究,文献[23]提出针对虚拟阻抗的电压补偿方案,解决了虚拟阻抗带来的电压跌落问题,提高了电能质量。

考虑到变流器运行状态会发生变化,以及系统中线路阻抗等重要参数会发生偏移,更为灵活的自适应虚拟阻抗技术受到关注与研究[24-26]。文献[24]在传统虚拟阻抗的基础上加入了自适应叠加项以修改电压参考值,并通过电压恢复机制补偿相应的输出电压降低,实现了有功功率与无功功率的合理分摊。文献[25]根据输出功率因数自适应调节虚拟阻抗的阻抗角,解决了在部分工作点仅仅调节虚拟阻抗的模无法提供电压补偿的问题,提高了系统的鲁棒性。文献[26]基于一致性控制提出了一种自适应阻抗控制,提高了无功功率的分配精度,并降低了系统对于通信的要求。

但是包含上述在内的研究大都以功角(本文将分布式电源输出电压与并网点电压间的夹角定义为功角,与文献[27]系统处于稳态时功角定义相同)很小作为基本条件,鲜有文献讨论功角较大时候所造成的功率耦合问题,而在实际当中,小功角的条件并不能时刻满足[28]。VSG拥有频率自调节能力,当给定有功功率增加,或者当VSG所接入的电网频率突然降低时,VSG输出频率根据虚拟转子惯量时间常数做出相应的响应,功角也随之被拉大,造成功角的变化,随之对无功功率产生影响,且随着功角的增大,功率耦合情况愈发严重。

本文首先介绍了典型VSG控制策略,然后分析了在VSG并网时,由于低压线路阻抗相较于高压线路阻性比例提高呈现出阻感特性,进而造成功率耦合程度加强。虽然虚拟负阻抗等方式能够实现功率解耦,但是当功角足够大的情况下,仍然存在耦合现象。为此,文中通过建立VSG并网时功率与频率的响应模型,分析了VSG出现大功角的本质原因。进一步,提出基于自适应虚拟阻抗的功率解耦控制方法,通过虚拟阻抗的实时变动以补偿功角所带来的影响,解除有功功率对无功功率所产生的影响。最后,在PSCAD/EMTDC搭建仿真模型并验证了所提出控制策略的正确性与有效性。

1 VSG控制及功率耦合分析

1.1 典型VSG控制

典型VSG系统框图如图1所示,其中，直流侧电压Vdc由清洁能源或储能装置提供,视作VSG的原动机部分;eok(k=a,b,c)为滤波器电容电压,本文称之为VSG输出电压;uk为电网电压;isk和ik分别为逆变器输出电流及并网电流;isd,isq和id,iq分别为isk和ik的dq轴分量;eod和eoq分别为eok的dq轴分量;eodref和eoqref,isdref和isqref,uod和uoq分别为虚拟阻抗控制的输出量、电压环控制的输出量、电流环控制的输出量的dq轴分量;L,RL,C分别为逆变器LC滤波器的电感、电感寄生电阻及电容;Lg和Rg分别为逆变器输出电压与并网点电压之间输电线路的等效电感与电阻,并定义Lg所对应的感抗值为Xg;PWM表示脉宽调制;PI表示比例—积分。

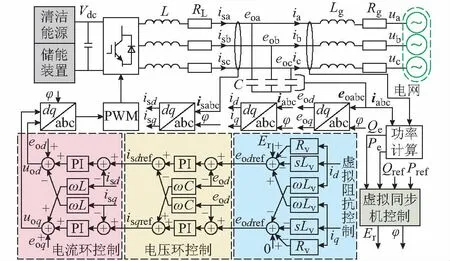
图1 典型VSG系统Fig.1 Typical VSG system

VSG有功功率—频率控制的核心是引入转子运动方程以模拟同步机转子的惯量与阻尼特性,为进一步模拟同步机对频率的响应特性,下垂控制也被引入其中,具体表达式如式(1)所示。

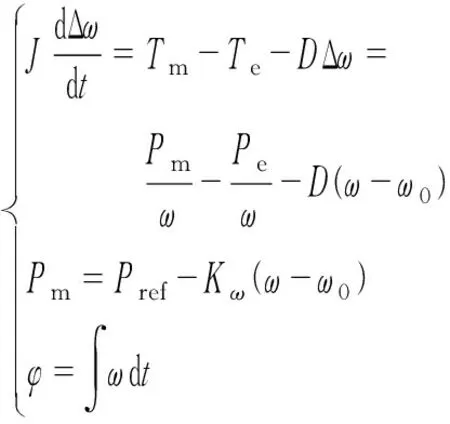
(1)

式中:J和D分别为转动惯量和阻尼系数;ω,ω0,Δω分别为VSG内电势旋转频率、额定频率及二者的偏差值;Pref为有功功率的参考值;Pm和Pe分别为VSG的机械功率与电磁功率(实际输出功率);Tm和Te分别为相对应的机械转矩与电磁转矩;Kω为有功功率—频率控制的调节系数;φ为虚拟转子角,即VSG输出电压的相位。需要说明的是,由于ω与ω0一般相差不大,故式(1)中转矩的求取可以简化为Pm和Pe与ω0的相除。

另外,VSG还需具有电压调节能力,通过无功功率下垂控制进行调节。即

Er=E0+KQ(Qref-Qe)

(2)

式中:E0和Er分别为VSG的空载电动势及所计算出的电动势给定值;Qref和Qe分别为无功功率参考值及实际值;KQ为无功功率下垂调节系数。

由此可以得到VSG控制框图如附录A图A1所示,所得到的虚拟转子角及电动势给定值进一步将作为内环控制环的给定信号。

为实现功率的精确分配与控制,可在控制系统中加入虚拟阻抗控制[29],图1中虚拟阻抗具体控制方程可以表述为:

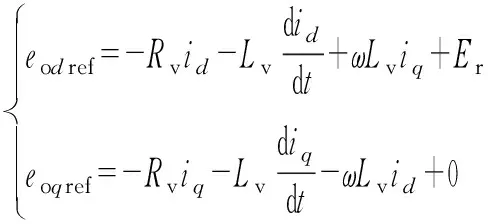
(3)

式中:Rv和Lv分别为虚拟电阻与电感,为便于后续分析,将Lv所对应的感抗值以Xv表示,Xv=ωLv。

1.2 功率耦合机理分析

典型下垂控制中,为便于分析,一般会假设线路阻抗为纯感性或纯阻性,但实际上线路阻抗参数并非理想状态,感抗与阻抗所占比例可能处于同一数量级,尤其低压配电网中线路阻抗的阻性成分甚至大于感性成分,对逆变器输出功率控制提出更高要求。

图1中VSG的功率传输模型可等效为VSG输出电压经线路阻抗串联至并网点,如附录A图A2所示。附录A图A2中,Eo为VSG输出电压有效值;考虑到Ug为并网点电压,假设其相位为基准相位,则δ便为Eo与Ug间的相位差。类似于传统同步电机定义内电势与电机机端电压的差角为功角,这里将VSG输出电压与电网电压的相位差角δ定义为功角。显然可知线路电流可表示为:

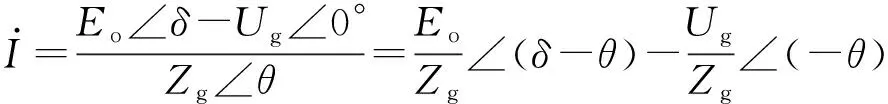
(4)

式中:Zg和θ分别为线路阻抗的模值及阻抗角。

进一步可推导得逆变器馈入电网的功率为:

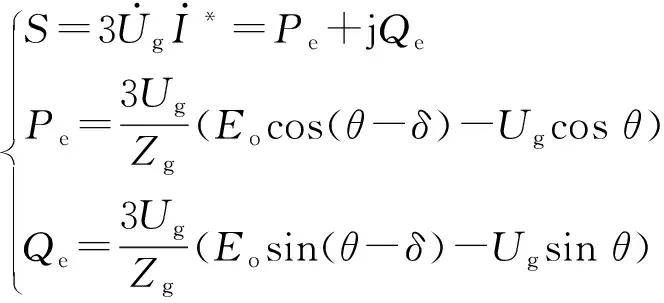
(5)

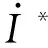
对Pe和Qe求关于Eo和δ的偏导数可得:

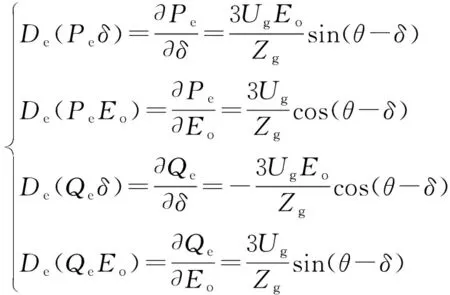
(6)

从控制角度,期望以Eo和δ作为控制量,以Pe和Qe作为被控量,并且控制为两个相互独立的单输入单输出系统。而根据式(5)可知,Eo和δ同时作用效果于Pe和Qe,控制系统存在耦合,且随着阻抗角θ的增大,耦合关系加强,显然不满足Pe和Qe独立控制的目标。

当线路阻抗呈现阻感性时,为对功率进行解耦控制,最常见的控制策略是通过虚拟电感、虚拟负阻抗等方法,改变逆变器控制环路参数,使得逆变器输出电压与电网电压间等效阻抗接近于纯感性,此时式(5)可改写为:

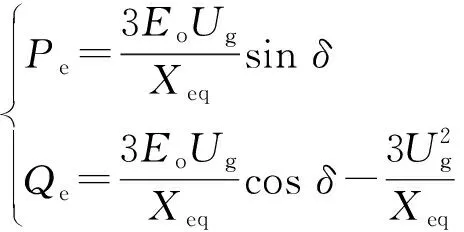
(7)

式中:Xeq为解耦后线路等效感抗值。

对式(7)状态变量进行改写,得到其小信号模型为:

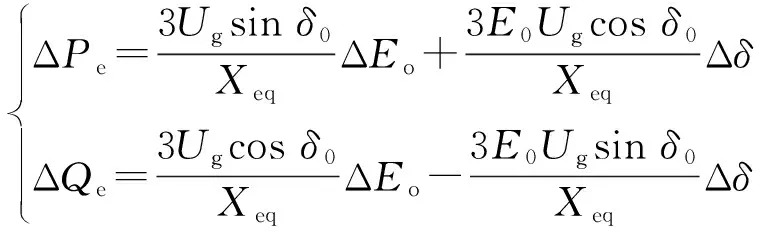
(8)

式中:E0和δ0分别为VSG输出电压及功角的稳态分量;ΔPe,ΔQe,Δδ,ΔEo分别为有功功率、无功功率、功角及VSG输出电压的小扰动分量。

观察式(8)可发现,即使等效阻抗呈现感性,在功角足够大的情况下,有功功率与无功功率仍旧同时受到VSG输出电压与功角控制,存在功率耦合。随着功角的增大,功率耦合情况会逐步加重,而且功角值与线路所传输有功功率相关,并不固定,进一步为功率解耦控制带来不便之处。

为进一步具体阐述功角对于功率耦合的影响,对式(8)中ΔQe等号右边两项的绝对值分别作关于ΔEo和Δδ的关系图如图2所示。值得说明的是,为便于分析与作图,假设E0≈Ug=220 V;并假设线路等效阻抗呈现纯感性,为0.315 Ω。

图2中,功角稳态工作点为2°时对应S1和C1平面,功角稳态工作点为10°时对应S2和C2平面,其中S1和S2平面表明的是ΔQe与ΔEo之间的增益关系,由图2可见功角的增大对这部分的影响比较小;而C1和C2平面表明的是ΔQe与Δδ之间的耦合关系,可以看出功角稳态工作点的增加可以明显加重功率的耦合程度,功率解耦需要纳入考虑范围。

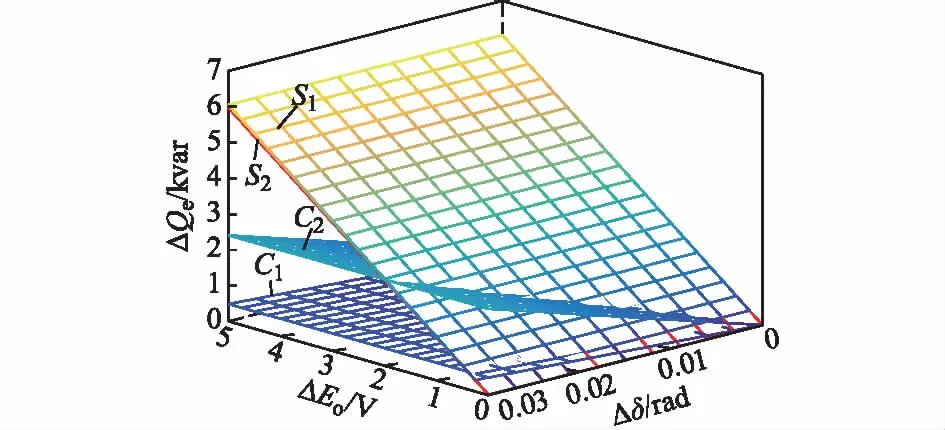
图2 功角对功率耦合的影响Fig.2 Effect of power angle on power coupling

1.3 考虑VSG功角影响的功率解耦的必要性

电力电子设备的控制具有多时间尺度的特点[30],而目前关于VSG频率响应的时间尺度方面,诸多研究都不统一,但根据VSG对于电网调节能力的意义以及对于传统同步电机的模仿,其频率响应时间可以做到秒级,而传统逆变器的电压、电流内环控制则可以达到毫秒级,二者响应速度有明显差距。基于此,为便于VSG功角特性的分析,可做如下假设:①将双闭环忽略不计,视VSG输出电压能够快速跟随给定电压;②暂不考虑无功环路对有功环路的耦合影响,并根据式(8)得到ΔPe=(3E0Ug·cosδ0/Xeq)Δδ=KΔδ。

基于上述假设条件,观察附录A图A1中VSG基本控制可以得出,当电网频率发生波动,抑或功率给定指令有大的调整,VSG调频控制起到作用。另外,通过对式(1)改写,可以得到其小信号模型如下:

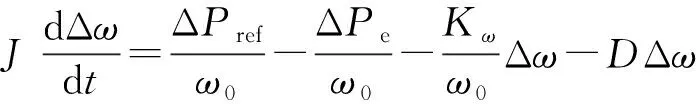
(9)

式中:ΔPref为Pref的小扰动分量。

根据前文对于功角的定义,即VSG输出频率与电网频率之间角频率偏差的积分为功角,进一步可将附录A图A1中控制框图化简得到VSG功率—频率的闭环控制框图如附录A图A3所示。图中:Δωg为电网频率ωg的波动值,定义为Δωg=ω0-ωg。

根据附录A图A3控制框图,可以得到功率给定发生变化时,相应的功率—频率传递函数为:

(10)

电网频率发生波动时,相应的电网频率—VSG频率传递函数为:

(11)

考虑VSG功率指令发生突增,以及假设电网频率发生了最为苛刻的突然下降,可得到传递函数GP-ω(s)和Gω-ω(s)典型的响应曲线,如附录A图A4所示。

动态情况下,功角变化量其实为VSG输出频率ω与电网频率ωg偏差的积分量,当VSG给定功率指令发生突变,并假设电网频率稳定,则此时功角变化的大小取决于VSG输出频率的速度,如附录A图A4(a)中阴影部分面积所示。当系统参数固定,阴影部分面积将与给定功率指令变化量呈正相关关系,当给定功率变化值足够大,功角将不再是传统所认知的足够小。当电网频率突然下降,VSG频率以与虚拟转动惯量相关的时间常数缓慢减小,反映了VSG对电网频率的支撑作用,但同时由于VSG输出频率与电网频率存在偏差,功角也进一步增大,如附录A图A4(b)中阴影部分面积所示,而同时这部分增大的功角也体现了VSG馈入电网有功功率的提高。此时功角的大小变化不仅与系统的响应特性有关,还与电网频率的波动大小和波动方式有关,功角足够小也必然不能一直满足。

从前文分析可知,即使利用典型的虚拟阻抗法将等效线路阻抗设计为纯感性,但当功角足够大时,有功功率与无功功率仍然存在耦合,所以考虑功角的功率解耦具有现实意义。上述功角变大的情况出现在有功功率控制环路,体现的是VSG对功率给定值增大与电网频率波动的响应,而这部分响应所带来的问题是对无功功率的耦合影响,所以本文主要解决在VSG功角影响下有功环路对无功环路的影响。

2 自适应虚拟阻抗功率解耦控制

2.1 自适应虚拟阻抗功率解耦控制机理

基于自适应虚拟阻抗的VSG功率解耦控制主要解除的是功角对无功功率的影响,即有功功率对于无功功率的影响,而功角因功率给定值及电网频率波动值的变化而变化,并不固定。

典型的虚拟阻抗控制相当于是以参考电压减去虚拟阻抗上的压降作为微电源的参考值,表达式如下:

Eoref(s)=Er(s)-(Rv+sLv)I(s)

(12)

式中:Eoref为电压环控制的给定值;Er为上层VSG控制所输出的电动势给定值。值得说明的是这里的虚拟阻抗取值不单单局限于正值,也同样可取负值,比如就有学者所提出的“虚拟负阻抗控制”控制策略。

为简化分析,忽略内环电压、电流闭环控制,认为控制系统能够实时跟踪到式(12)所给定的参考值,进一步可以得到如附录A图A5所示的加入虚拟阻抗的VSG系统,可以看出所加入的虚拟阻抗相当于是与VSG输出电压和电网电压之间传输线路的阻抗相串联。

此时附录A图A2中用来传输功率的线路阻抗则不再只含有线路阻抗,而是广义上总的系统阻抗Z,包括虚拟阻抗和线路阻抗两部分,可以写为:

Z=(Rg+Rv)+jω(Lg+Lv)=R+jX

(13)

当功率给定值突增或者电网频率发生突然下降,进而使得功角被拉大Δδ至不可忽略的数值,如果控制系统不作出响应,无功功率将被之影响。自适应虚拟阻抗功率解耦控制的核心思想是以式(5)中阻抗角θ为间接参变量,并以Rv和Lv为直接变量调节θ,进而通过合理调整θ的大小实时补偿功角的波动量。但θ的变化无疑又对无功功率变化产生新的影响,所以θ值的选取还需考虑这部分的影响。与此同时,设计调节θ的同时,希望阻抗Z尽量保持恒定,这样不仅能够减小参变量的引入,而且避免了虚拟阻抗所带来的电压降问题。其次,VSG输出电压对于无功功率的控制属于正常的无功功率控制,不考虑这部分控制需求,而仅仅考虑θ与δ对无功功率所带来的影响,并根据式(5)得到相应的小信号模型:

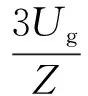
(14)

式中:θ0为阻抗角的稳态分量。

如前文所述,阻抗角的变化量应该包含两部分,即

(15)

式中:Δδ*所对应的量用来补偿功角的变化;Δθ*所对应的量则用来补偿θ自身变化所带来的新的无功功率影响,并期望无功波动量为零。

将式(15)代入式(14)得到:

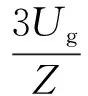
(16)

进一步可从式(16)推导得出:

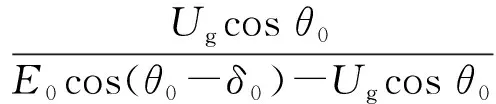
KconstΔδ*

(17)

式中:Kconst为与稳态工作点相关的常量值。

联合式(15)及式(17)可以得到:

Δθ=(1+Kconst)Δδ

(18)

并根据阻抗幅值及阻抗角定义,从式(13)得到:

(19)

(20)

将上式改写为相应的阻抗及阻抗角的小信号模型,并考虑到期望阻抗Z幅值保持恒定的条件,有

(21)

(22)

式中:R0和X0分别为电阻及感抗的基准值,参数选取为线路阻抗值的大小;ΔZ,ΔR,ΔX分别为阻抗、电阻及感抗值的可控小扰动分量。

进一步,将式(21)与式(22)代入式(18)当中,可以推出为抑制功角变化量所带来的无功功率波动,阻抗值所需改变量为:

(23)

在控制的实现过程当中,线路阻抗Rg和Lg无法改变,而仅仅只能通过改变虚拟阻抗值调整总的系统阻抗,故式(23)中ΔR和ΔX值也就是虚拟电阻Rv与虚拟电感值Xv所需改变量。

自适应虚拟阻抗功率解耦控制根据功角值来实时调节虚拟阻抗值的大小,功角的估算则成为重要的环节。式(5)中VSG输出有功功率特性相比同步电机功角特性稍显不同,但是特性具有相似之处,考虑到功角特性曲线具有非线性特征,以及本文所针对的功角为简化控制算法,在稳定工作点附近仍旧采用局部线性化处理,功角估算曲线为:

Δδ=KcorΔPe=Kcor(Pe-P0)

(24)

式中:P0为VSG稳态工作点输出功率;Kcor为功角波动量估算式中的比例系数,其由两部分组成,如式(25)所示。

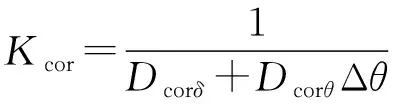
(25)

式中:Dcorδ为式(6)中偏导数De(Peδ)的线性化近似结果,具体线性化计算可用附录A图A6功角特性曲线进行确定；Dcorθ为对Kcor进行修正的修正系数。

曲线C为对式(5)所描述的功角曲线,a(δ0,P0)为额定工作点,b(δb,Pb)点为C上距a点较近的一点(选取Pb=1.25P0),并以a和b点间斜率作为曲线A的斜率,即Dcorδ的参数。功角与功率间的关系为非线性关系,线性化的计算会带来误差,且VSG输出功率偏离额定功率越大,使用式(24)所估算得到的功角误差越大,如附录A图A6中,功角曲线e点相比c点,距离功角估算曲线A越远,误差越大。为减小功角估算误差,本文采取多条功角估算曲线配合使用的控制策略,依然如附录A图A6所示,曲线A与功角曲线ac段相近,而与功角曲线ce段间偏差较大,故选择另一功角估算曲线B,使其与功角曲线ce段误差较小。

具体实施方式为选取多组如式(24)的功角估算曲线,各条曲线稳态工作点相同,唯一不同的是Dcorδ的取值,其选取规则可以表述为矩阵H:

H=[(Dcorδ,0,[P0,P1]) (Dcorδ,1,[P1,P2]) …]

(26)

式中:Dcorδ,i(i=0,1,…)为第i条曲线斜率;[Pi,Pi+1]为第i条曲线所使用的功率范围,并选取Pi+1=Pi+1+0.5P0。

第i条曲线斜率确定方法与曲线A的斜率确定方法类似,如附录A图A6中曲线B比例系数以a和d(δd,Pd)点进行确定,Pd=P1+0.25P0。

控制过程中,系统根据输出功率大小进行曲线选取,当输出功率处于H中的第i条功角估算曲线的功率范围[Pi,Pi+1]时,则功角估算曲线切换至第i条功角估算曲线。

观察式(18),相对于功角,阻抗角的变化更为明显,进一步会对局部线性化处理所得到的Dcorδ造成影响,为此引入Dcorθ项进行修正,根据式(6)有以下等式。

(27)

2.2 自适应虚拟阻抗参数分析

然而在实际控制系统中,受到控制器延时[31]等多方面影响,输出信号并不能实时精确地跟踪给定值,所以上文所分析的虚拟阻抗值也同样受到控制系统参数的影响。本文VSG控制信号经如图1所示的电压、电流闭环进行控制,电压与电流控制环均在dq坐标系下采用PI控制器进行前馈解耦控制,并在双闭环控制策略中加入虚拟阻抗,具体控制框图如附录A图A7所示,对其进行分析可得VSG输出电压为:

eodq=G(s)erdq-Zo(s)idq=

(28)

式中:G(s)为参考电压与输出电压间的传递函数;Zo(s)为加入虚拟阻抗后VSG等效输出阻抗;其余参数表达式见附录B式(B1)。

观察系统特征方程式(29)可以发现,系统特征方程与虚拟阻抗参数无关,系统控制环路的稳定性不受虚拟阻抗参数的影响,通过合理设计双闭环PI控制器参数就以使控制环路稳定。为确保整个VSG并网系统稳定,须保证Rv>-Rg[22]。

D(s)=a4s4+a3s3+a2s2+a1s+a0

(29)

实际控制中,VSG输出阻抗并非等于所设置的虚拟阻抗大小,而是含有加入虚拟阻抗后的逆变器等效输出阻抗,如式(28)中Zo(s)所表述。以逆变器主要参数(如附录A表A1中所示)为例,分别加入虚拟电阻与虚拟电感,可以得到系统等效阻抗波特图,如附录A图A8所示。

由附录A图A8(a)可以发现,加入Rv后并随着Rv的增大,系统等效输出阻抗更偏向于阻性,而且阻抗随之增大,阻抗角则减小。另一方面,如附录A图A8(b)所示,加入Lv后系统的等效阻抗与阻抗角都随着Lv的增大而增大,等效阻抗无疑更偏向于感性。进一步,可以通过合理调节虚拟阻抗值,使得系统的等效输出阻抗满足前文所分析的解耦控制条件,取得满意的控制效果。

基于自适应虚拟阻抗的功率解耦控制通过输出功率大小估算出功角大小,进一步计算出虚拟阻抗值用以解除有功功率控制回路对于无功功率的影响,整体控制框图如图3所示。

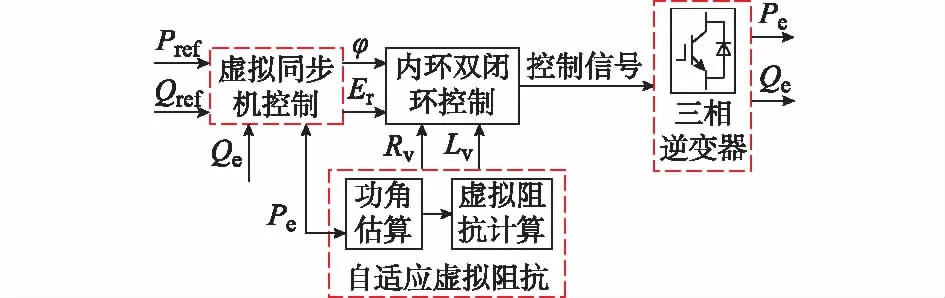
图3 自适应虚拟阻抗功率解耦控制系统Fig.3 Power decoupling control system based on adaptive virtual impedances

3 仿真分析

为验证本文所提出的基于自适应虚拟阻抗的VSG功率解耦控制策略,利用PSCAD/EMTDC搭建图1中的VSG并网系统,主要参数见附录A表A1和表A2。值得说明的是,线路阻抗参数的选取是基于线路采用型号LJ-70(1 km)导线[15]。

初始状态下,VSG稳定地向电网馈送有功功率为20 kW,无功功率为5.5 kvar。设置t在2～4 s期间,电网频率下降0.1 Hz;t=6 s时,VSG有功功率给定值增加20 kW,图4是VSG并网运行时功角的变化曲线。

图4 VSG功角曲线Fig.4 Power angle curve of VSG

由图4可以看出,在电网频率下降或有功功率给定值大幅度增加时,功角都明显变大,进一步能够对功率耦合造成影响,证明了前文对于功角变大理论分析的合理性。

3.1 仿真案例1:电网频率下降

为考察电网频率下降引起VSG功角变大时造成的功率耦合现象及解耦控制的有效性,设置电网频率在t=3 s时下降0.1 Hz,附录A图A9为不同解耦控制的功率输出效果。附录A图A9(a)给出的是不同控制下,即不加解耦控制、加入虚拟负阻抗控制及加入自适应虚拟阻抗解耦控制时的有功功率变化情况,三种控制模式下的功率曲线互相重叠,证明VSG有功功率自身的控制不因解耦控制的不同而受到影响,即解耦控制的不同对有功控制环路没有明显影响;从附录A图A9(b)可以看出,电网频率下降时,VSG输出的无功功率也出现相应的变化,与附录A图A9(a)中的有功功率存在耦合;为解除系统功率耦合,在控制环路中加入虚拟负阻抗控制,仿真结果如附录A图A9(c)所示,功率耦合情况得到减弱,但有功功率环路仍对无功环路存在影响,功率耦合无法清除,证明功角过大时虚拟负阻抗解耦控制存在局限性;将本文所提出自适应虚拟阻抗解耦控制策略加入至控制环路,得到附录A图A9(d)仿真结果,可以看出电网频率下降后无功功率仍旧能够保持原来的稳定值,解耦效果明显。

为进一步量化地比较上述工况下无功功率的变化,将控制系统不加解耦控制、加入虚拟负阻抗控制及加入自适应虚拟阻抗控制时的无功功率变化量及变化后进入稳态的无功功率值进行对比,如附录A表A3所示。可以清晰地看出,自适应虚拟阻抗控制保证了无功功率控制环路不受有功功率控制环路的影响,控制效果良好。

3.2 仿真案例2:给定功率大幅度增加

另一种会造成功角变大的工况是给定功率的大额增加,同样在初始状态下,VSG稳定地向电网馈送有功功率20 kW,并设置t=2 s时给定功率增加15 kW,t=4 s时给定功率继续增加10 kW,即分别相对初始状态下VSG输出有功功率阶跃增加了75%和50%。附录A图A10为相应的不同解耦控制下功率输出效果。

如附录A图A10(a)所示,在不同控制下,即在不加解耦控制、加入虚拟负阻抗控制及加入自适应虚拟阻抗解耦控制时,有功功率按照设定值进行输出,不同解耦控制策略的使用对原有有功功率的控制没有额外影响;但是如附录A图A10(b)所示,在不加解耦控制的情况下,无功功率受到有功功率控制的影响,分别在有功功率给定值增加的两个时刻也相应地发生变化;如附录A图A10(c)所示,加入虚拟负阻抗解耦控制也并不能实现无功功率与有功功率的解耦,无功功率仍然受到有功功率影响而出现下降;将本文所提出自适应虚拟阻抗解耦控制加入至控制环路,得到附录A图A10(d)所示无功功率曲线,可看出此时有功功率的变化不再对无功功率产生耦合影响。

同样,为量化地比较无功功率的控制效果,将控制系统不加解耦控制、加入虚拟负阻抗控制及加入自适应虚拟阻抗解耦控制时的无功功率变化量及变化后进入稳态的无功功率值进行对比,如附录A表A4所示。可以明显看出,自适应虚拟阻抗解耦控制保证了无功功率始终保持在稳定工作点,达到了解耦的目的。

4 结语

中低压配电网环境下,VSG接入的电网线路阻抗呈阻感特性,功率解耦控制可通过传统虚拟阻抗方法实现。但即使将等效输出阻抗控制为纯感性,在功角过大的情况下,VSG的输出功率仍存在功率耦合现象。通过小信号模型分析可知，电网频率下降与有功功率给定值的大幅度增加是导致VSG功角变大的主要因素。本文为消除功角对于功率耦合的影响,提出了基于自适应虚拟阻抗的VSG功率解耦控制策略,能够根据输出功角的变化自主改变虚拟阻抗值大小,满足VSG功角过大时的功率解耦控制要求。但是,本文重在考虑消除有功环路对无功环路的影响,存在局限性,下一步需完善功角影响下的功率解耦控制。

本文受到内蒙古电力集团(有限)责任公司科技项目(内电科信〔2017〕46号)资助,特此感谢!

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。