电网电压骤降恢复对双馈风电机组连锁脱网的影响

周步祥, 董 申, 林 楠, 刘舒畅, 张 冰, 赵 磊

(1. 四川大学电气信息学院, 四川省成都市 610065; 2. 国网四川省电力公司, 四川省成都市 610041;3. 四川电力设计咨询有限责任公司, 四川省成都市 610065; 4. 国网江苏省电力有限公司电力科学研究院, 江苏省南京市 211103)

0 引言

随着各国对清洁能源的重视,风电随着技术的突破革新,取得了瞩目的发展[1-2]。在目前的风电工程实践中,国内各地曾先后发生了多次风电机组连锁脱网事故[3-5]。而这些事故都是先发生了电压骤降故障,后引起电压骤升故障之后导致风电机组脱网。

目前在双馈风电机组故障分析领域,对双馈风电机组动态特性和骤升故障方面有着较多的研究[6-14],在动态特性方面,文献[6-7]在转子侧的视角下对双馈风电机组的动态特性进行分析,剖析了风电机组故障的作用机理;文献[8-9]分析了双馈风电机组暂态电势的动态特性,为双馈风电机组暂态模型的建立提供了理论依据。在优化骤升故障能力方面,文献[10-11]采用串联网侧变换器应对骤升故障,通过抑制定子磁链的暂态直流分量,提高了高电压穿越能力;文献[12]采用基于虚拟阻抗的控制策略,缩短了电网电压骤升时的转子振荡过程,优化了双馈风电机组的高电压穿越能力;文献[13-14]提出了以无功支持为基础的控制方案,使电压能够很快恢复并保持稳定,优化了双馈风电机组的骤升故障穿越性能。但是以上这些研究中对风电机组动态特性的分析和采用的风电机组暂态模型只考虑到了单一故障,没有考虑到实际工况中短时两次或多次故障出现的概率,未深入全面反映双馈风电机组在故障运行中的暂态特性。同时由文献[3-5]可知,在短时两次连锁故障情况下,电网电压骤升故障在电网电压骤降故障恢复后发生的概率较大。当出现该类型故障时,第一次故障将会对后面发生的故障产生影响。

基于此,本文通过考虑电网电压骤降恢复阶段,建立计及该阶段的暂态数学模型,详细分析该阶段对双馈风电机组动态特性和高电压穿越过程的影响,尤其是定子磁链自由分量的影响,推导出考虑电压骤降恢复阶段的定、转子表达式,以定、转子电流为参考,量化考虑该阶段的性能指标。最后,详细剖析电压骤降恢复和电压骤升两个阶段的故障参数对高电压穿越过程的影响,使该模型的性能指标更加清晰。同时,为分析双馈风电机组动态特性和对高电压穿越的影响提供了精确的暂态模型和定、转子电流计算公式。

1 双馈风电机组骤升故障过程及暂态模型

1.1 双馈风电机组骤升故障过程

从文献[3-5]提到的脱网事件中可以看到,电压骤升故障往往出现在低电压穿越故障之后,在电网电压骤降恢复阶段,由于系统无功过剩和部分双馈风电机组不具备高电压穿越能力而导致电网骤升故障,双馈风电机组电压骤升故障过程中电网电压波形如图1所示。

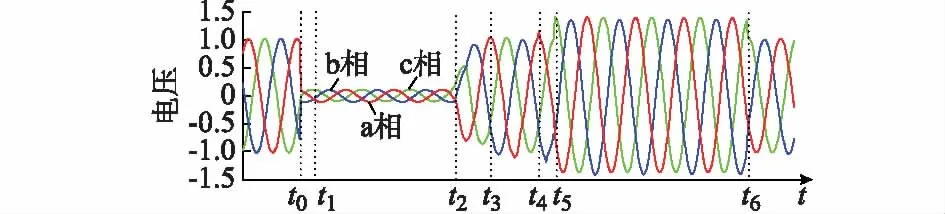
图1 电网电压骤升故障波形Fig.1 Voltage waveform under voltage surge fault of power grid

图1给出了电压骤降故障恢复后引起了电压骤升故障的电网连锁故障情况,其中电压为标幺值。电网故障发生在t0时刻引起电压骤降,骤降深度为p,在满足一定条件时,t0时刻Crowbar开始投入,t1时刻断开,双馈风电机组将逐渐在低电压下运行进入稳态。在t2时刻,故障保护投入,电网电压开始恢复,以三相短路故障为例,如果考虑断路器实际运行情况,三相短路故障会首先恢复为两相短路故障,并且大约在10 ms后的t3完全恢复[15]。之后双馈风电机组将逐渐恢复输出有功功率并进入正常运行状态。由于发生低电压穿越故障后,系统大量补充无功功率,导致在t4时刻发生电压骤升故障,骤升幅度为m,同样在满足一定条件时,转子侧投入Crowbar,t4时刻投入,t5时刻切除。t6时刻故障电压再次恢复。本文针对t2～t6时刻,只讨论电网对称故障情况。

1.2 双馈风电机组暂态模型

1)不考虑电网电压骤降恢复阶段

不计磁饱和现象,在定子坐标系为基础的空间矢量坐标系下双馈风电机组定、转子电压和磁链方程式如下[16]:

(1)

(2)

ψs=Lsis+Lmir

(3)

ψr=Lrir+Lmis

(4)

式中:Lm为励磁电感;Ls,Lr和Rs,Rr分别为定子、转子全电感和电阻;is,ir和ψs,ψr分别为定、转子电流和磁链;ωr为转子转速。

忽略定子电阻,由式(1)和参考文献[17-20]可分别得到双馈风电机组正常运行时的定子总磁链(强制分量)、定子磁链自由分量和不考虑恢复阶段的定子磁链初始自由分量,如下式所示。

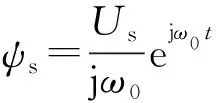
(5)

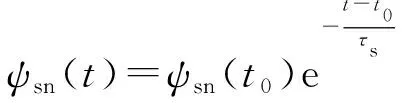
(6)

ψsn(t4)=ψs(t4)-ψsf(t4)=

(7)

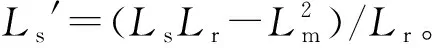
2)考虑电网电压骤降恢复阶段

由上述案例和图1可知,多数电压骤升故障是发生在电压骤降恢复阶段之后,即t3时刻之后。虽然此时电网电压已恢复正常,但在t3时刻之后定子磁链自由分量仍然存在,这将直接影响到定子磁链的合成,因此电压骤降恢复阶段必然会对电压骤升故障产生影响。

由式(5)可知,定子磁链强制分量只受到电网电压和电网角速度的影响,当电网处于电压骤降恢复阶段中时,此时的电网电压已恢复正常,电网角速度恒定不变,对强制分量无影响。而由于恢复阶段中定子磁链自由分量仍然存在,电网电压骤降阶段对自由分量将产生明显影响,即ψsn(t4)将不同,进而影响双馈风电机组高电压穿越性能。

由式(6)和式(7)可知,自由分量只与骤升幅度m有关,而考虑到电网电压骤降恢复阶段,则电压骤降深度p、电网电压恢复正常到发生电压骤升故障的时间Tr、恢复时的电网故障角度θ等都会对磁链产生影响,所以考虑电网电压骤降恢复阶段的定子磁链自由分量关系式ψsn(t4)应如式(8)所示。下文将通过对双馈风电机组的故障动态特性进行分析,给出ψsn(t4)的具体解析式。

ψsn(t4)=f(m,p,Tr,θ,…)

(8)

2 考虑电网电压骤降恢复阶段的双馈风电机组骤升故障动态特性分析

2.1 电网电压骤降恢复阶段

1)骤升故障发生前的定子总磁链ψs(t4-)

由上文可知,电网电压在t2时刻恢复时,双馈风电机组已在低电压下工作在稳定状态,此时只存在由剩余电网电压产生的强制分量,如式(9)所示。

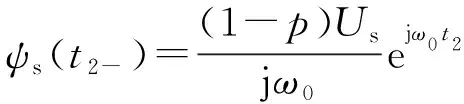
(9)

之后某相断路器将会在电流过零时先断开,三相短路故障将会变为两相短路故障。故障开始恢复的相对时间可以由故障电压、电流之间的角度θ表示,称为故障恢复角。此时θ满足以下关系[21]:

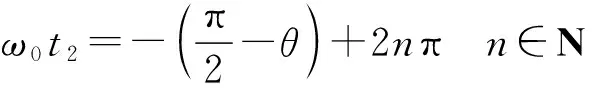
(10)

θ的大小主要与故障点和风力发电系统之间的线路阻抗有关,通常情况下在分布系统中故障角度范围为45°～60°,在传输系统中故障角范围为75°～85°[4]。

由对称分量法可知[16],t2+时刻强制分量ψsf(t2+)由正、负序部分组成,如式(11)所示。

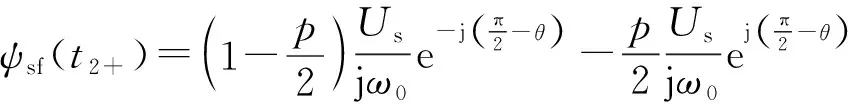
(11)

由于t2时刻磁链不能突变(ψs(t2+)=ψs(t2-)),因此可知自由分量ψsn(t2+)为:

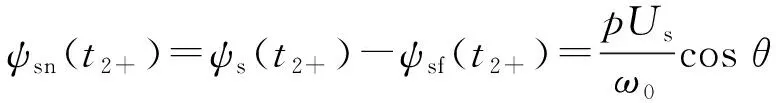
(12)

大约10 ms后,强制分量正、负序部分大约旋转90°到达t3时刻,此时剩余两相恢复,电网电压恢复正常。由于矢量控制下τs常数较大(1 s左右),且衰减时间短暂,因此ψsn(t3)可以忽略衰减影响。ψs(t3+)如式(13)所示。

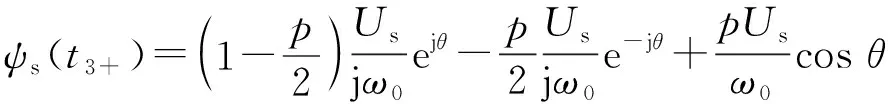
(13)

t3+时刻,电网电压恢复正常,ψsf(t3+)如式(14)所示。

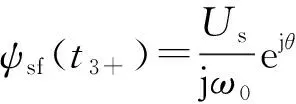
(14)

由于t3时刻磁链不能突变,可知ψsn(t3)表达式为:

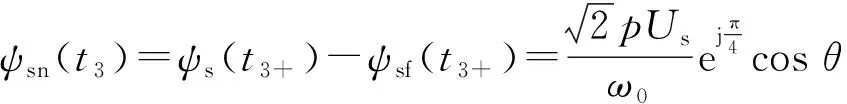
(15)

在骤降恢复阶段(t3～t4),ψsn(t3)为初始磁链,由式(6)和式(15)可知自由分量ψsn(t)表达式为:

(16)

强制分量ψsf(t)表达式为:

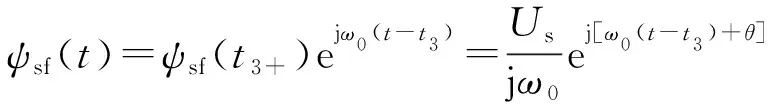
(17)

在发生骤升故障之前的t4-时刻,定子总磁链如下:

ψs(t4-)=ψsf(t4-)+ψsn(t4-)=

(18)

式中:Tr=t4-t3为电压骤降恢复正常到发生骤升故障时的间隔时间。

2)骤升故障发生前的转子总磁链ψr(t4-)

由于Lr=Lm+Llr,Ls=Lm+Lls,而Lm≫Llr,Lm≫Lls,因此Lm≈Lr≈Ls。其中,Lls和Llr分别为定、转子漏感。式(3)与式(4)联立可得:

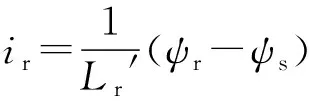
(19)

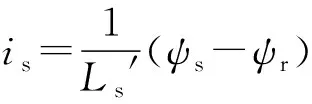
(20)

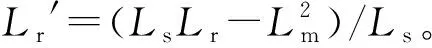
联立式(19)和式(20),将is用ir表示,可得:

is=-Kir

(21)

式中:K=Lr′/Ls′。

将式(19)代入式(2)可得ψr(t)的表达式,有

(22)

式中:τr为转子时间常数。

该微分方程初始条件为:

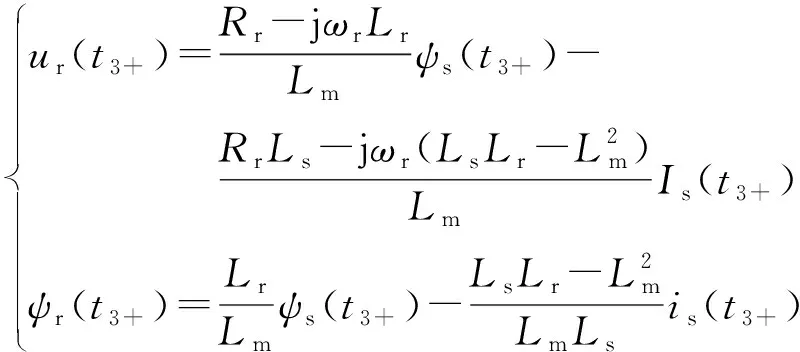
(23)

式中:Is为定子电流幅值。

忽略转子电阻,考虑到Lm≈Lr≈Ls这一条件,该微分方程初始条件为:

(24)

由式(22)和式(24)解得骤降恢复阶段的ψr(t)如下:

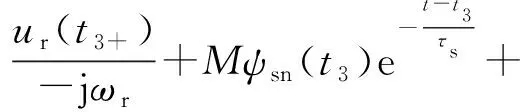
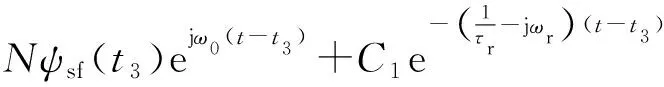
(25)

式中:M=1/(1-jωrτr);N=[1-ω0/(ω0-ωr)]/(1-jωrτr);C1=ψs(t3)-Mψsn(t3)-Nψsf(t3)+ur(t3)/(jωr)。ψr(t)及C1求解过程见附录A。

所以,ψr(t4-)表达式如下:

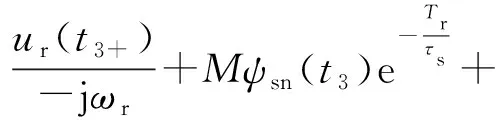
(26)

2.2 电压骤升故障阶段

1)骤升故障发生后的定子总磁链ψs(t)

骤升故障发生后定子总磁链ψs(t)和初始自由分量ψsn(t4+)的求解与骤升故障发生前定子总磁链和自由分量的求解类似,因此直接给出定子总磁链ψs(t)和自由分量的表达式ψsn(t4+),如式(27)和式(28)所示,具体求解过程见附录B。

(27)

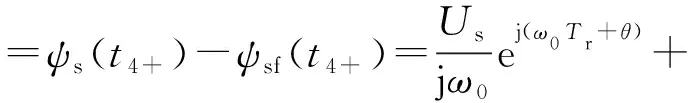
(28)

式(28)即为式(8)的具体表达式,由该式可知,考虑电压恢复阶段的定子磁链自由分量由两部分组成:第一部分由电压恢复阶段的自由分量决定,大小与p,Tr,θ有关;第二部分由骤升故障阶段的强制分量决定,大小与m,Tr,θ有关。同时,当ω0Tr+θ+π/4=2kπ(k=0,1,2,…)时,初始自由分量取得最大值。

2)骤升故障发生后的转子总磁链ψrc(t)

骤升故障发生后转子总磁链ψrc(t)的求解与骤升故障发生前转子总磁链的求解类似,因此直接给出转子总磁链的表达式ψrc(t),如式(29)所示,求解过程见附录C。

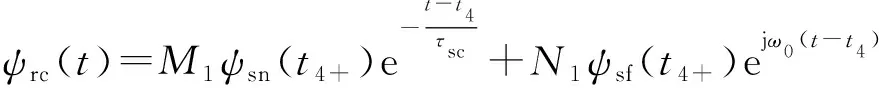
(29)

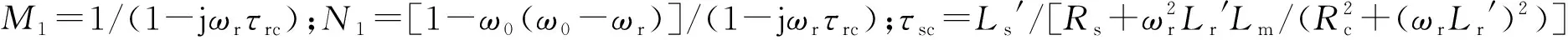
将式(27)和式(29)代入式(19)可得骤升故障阶段转子电流为:

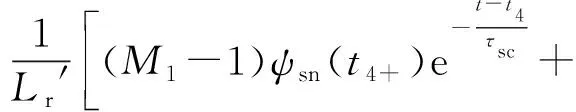
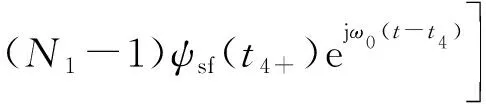
(30)

可知,当t=t4且满足ω0Tr+θ+π/4=2kπ(k=0,1,2,…)时,转子电流具有最大值Ircm,其表达式为:

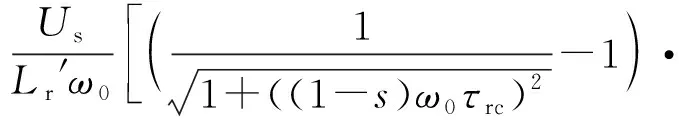
(31)

式中:s=(ω0-ωr)/ω0为转差率。

由式(31)可知,当Crowbar电路动作时,转子电流最大值受以下故障参数影响:故障恢复到骤升故障发生的时间间隔Tr、转差率s、电网电压骤降幅度p、电网电压骤升幅度m、故障恢复角θ和暂态转子常数τrc。由式(21)和式(30)可得骤升故障阶段定子电流为:

isc=-Kirc

(32)

由式(21)和式(31)可得定子电流最大值为:

Iscm=-KIrcm

(33)

由式(32)可以看出,在故障期间定子电流和转子电流方向相反,具有相同的变化规律,定子电流随着转子电流的增大而增大,并且两者最大值都在相同时刻取得。

3 电网电压骤降恢复阶段对高电压穿越性能的影响

3.1 定子磁链自由分量对高电压穿越性能的影响

当不考虑恢复阶段影响时,ψsn(t4+)如式(7)所示。当考虑该阶段影响时,ψsn(t4+)如式(28)所示。两者差值如式(34)所示。

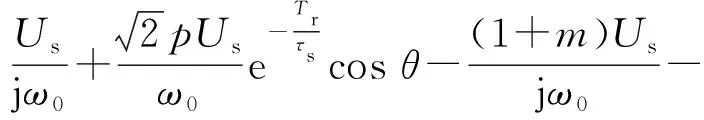
(34)

由式(34)可以看出,考虑恢复阶段影响时,骤升故障阶段的自由分量将会显著增加,进而使转子电流和定子电流增大。同时自由分量最大值与骤降故障的骤降深度p、故障恢复角θ和两次故障间隔时间Tr有关。采取控制变量法,取p=0.8(标幺值),θ=60°为默认参数。由于本文采用的双馈风电机组定子时间常数在矢量控制下约为1 s,因此以Tr=1 s为默认参数,从而避免定子时间常数远小于两次故障间隔时间时,发生定子磁链自由分量衰减完毕的情况。由此,得到图2所示的Δψsn与各影响参数之间的关系,其中Δψsn和p均为标幺值。

由图2可知,当考虑恢复阶段时,差值Δψsn最大为0.35Us/ω0,与不考虑该阶段的定子磁链自由分量相比增加了1倍之多,因此,骤降恢复阶段对自由分量有显著影响。由图2(a)可知,自由分量随着两次故障间隔时间的增大而减小,这说明了随着间隔时间的增加,自由分量逐渐衰减,对骤升故障阶段的影响也越来越小,当Tr→∞时,Δψsn=0,此时即为不考虑恢复阶段影响的自由分量;由图2(b)可知,自由分量随着骤降深度的增加而增大,表明了骤降深度越深,则此时磁链不平衡度越大,需要产生更大的自由分量来保持磁链平衡,当p=0时,Δψsn=0,此时也为不考虑恢复阶段影响的自由分量;由图2(c)可知,随着骤降故障角的增大,自由分量逐渐减小。

由式(18)和式(26)可知,不考虑恢复阶段影响时,Tr=t4-t3将趋向于无穷大,此时发生骤升故障前的定转子磁链ψs(t4-)和ψr(t4-)中的自由分量将为零。而考虑该阶段影响时,由于两次故障时间间隔Tr较短,自由分量将会出现。在式(18)和式(26)中,当参数Tr趋于无穷大时,此时的定、转子初始磁链便是不考虑电压骤降恢复阶段时的定转子初始磁链。通过t4-时刻定、转子总磁链自由分量为零这一结果,证明了上文所说结论,即电网电压骤降恢复阶段只对定子磁链自由分量有影响。

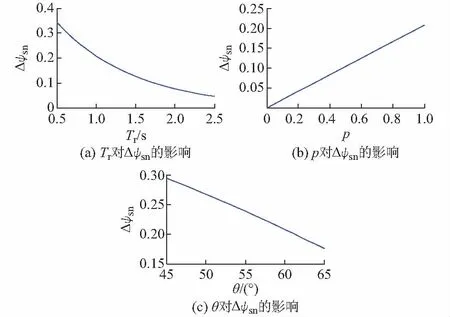
图2 Δψsn与各影响参数之间的关系Fig.2 Relationship between Δψsn and influencing parameters

3.2 不考虑电压骤降恢复阶段的定、转子电流

由上述分析可知,当骤降幅度为零(p=0)或两次故障间隔时间Tr→∞时,自由分量的差值将为零,此时即不考虑恢复阶段。由式(31)可知,当p=0或Tr→∞时,转子电流最大值如下:

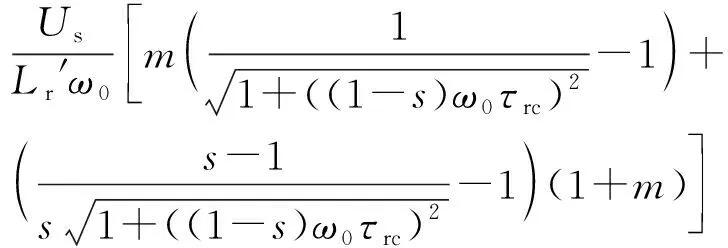
(35)

所以式(35)即为不考虑恢复阶段的转子电流。同理,可得定子电流最大值。由上式可知,不考虑该阶段时,转子电流最大值只受到骤升幅值m、转差率s和转子暂态常数τrc的影响,并未受到反映电压恢复阶段的参数p,Tr,θ的影响,验证了双馈风电机组动态特性分析的正确性。

分析不考虑恢复阶段时的条件“Tr→∞”可知,由于定子磁链自由分量的衰减函数为指数函数,在前几个衰减常数内可以快速衰减接近为0。因此,当α取某一正值时,条件“Tr→∞”将与条件“Tr>ατs”相等。此时可以说当Tr>ατs时,即可不考虑恢复阶段,α取值将在下文给出。

3.3 故障参数对高电压穿越性能的影响

由前文分析可知,定子电流与转子电流的值呈正比关系。因此,本文只对转子电流进行分析。为了量化各故障参数对高电压穿越性能的影响,定义eav为Ircm的最大值Ircmm相对于Ircm′的平均误差,求和步长为0.01,有

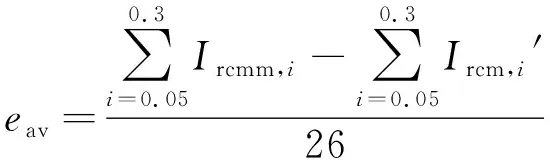
(36)

将双馈风电机组基本参数代入式(31)和式(35),采取控制变量法,取p=0.8,θ=60°,Tr=1 s,s=0.2,τrc=0.008 s为默认参数,可得到以各个故障参数为变量的转子电流最大值曲线如图3所示。以Tr为例,求取的误差为0.392(标幺值),表明考虑电网电压骤降恢复阶段转子电流最大值将会比不考虑该阶段增加0.392(标幺值)。计算各故障参数的误差,结果如下:eav,T=0.392,eav,p=0.377,eav,θ=0.426,eav,s=0.311,eav,τ=0.333,均为标幺值。双馈风电机组基本参数见附录D表D1。

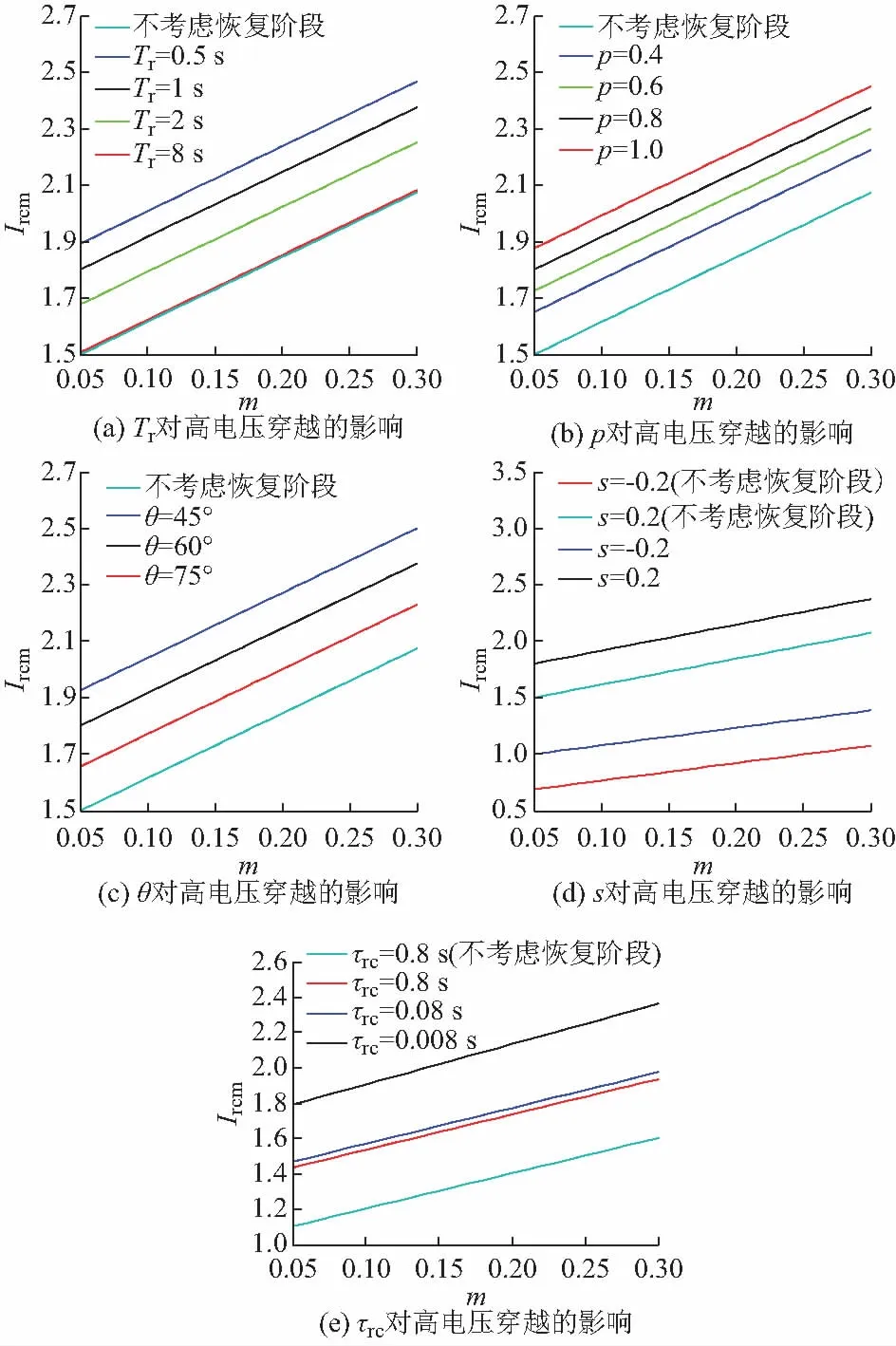
图3 不同故障参数下的转子电流最大值计算值Fig.3 Calculated values of maximum rotor current with different fault parameters

通过对考虑和不考虑电网电压骤降恢复阶段这两种情况进行对比,由以上数据可以看出,各个故障参数的平均误差都不为零且都为正值,说明考虑恢复阶段会使定、转子电流增大,进而影响到高电压穿越性能。同时,由于各故障参数的eav不同,反映出对高电压穿越性能的影响程度不同,根据eav的大小可知,各故障参数影响程度由大到小为θ>Tr>p>τr>s。由该结论可知,当考虑恢复阶段,在其他故障参数不变情况下,分布系统发生高压故障产生的过电流要比传输系统产生的过电流严重。

由图3可以看出,对于各个故障参数来说,随着自身参数值的变化,都会改变定、转子电流的大小,进而影响到高电压穿越性能。由图3(a)可知,转子电流随着Tr的增大而减小,说明两次故障间隔时间越长对高电压穿越性能的影响越小。同时,可看出Tr=8τs时的转子电流曲线与Tr→∞时的曲线几乎重合,此时定子磁链自由分量已衰减完毕,因此可取α=8。

由图3(b)可知,转子电流随着p的增大而增大,说明恢复阶段的骤降深度越大对高电压穿越性能的影响越大。由图3(c)和(e)可知,转子电流随着θ和τrc的增大而减小,说明故障恢复角和转子暂态常数越大对高电压穿越性能的影响越小。由图3(d)可知,当s=-0.2时,不论是否考虑恢复阶段,转子电流都不会出现过电流,此时对高电压穿越性能的影响很小。

4 仿真分析

4.1 骤降恢复阶段对高电压穿越影响的仿真分析

本节利用PSCAD对双馈风电机组的暂态过程进行仿真。仍采用附录D表D1中双馈风电机组的参数,故障前后风速不变,均为8 m/s,在t=2.7 s时发生对称骤升故障,各故障参数设置见附录E表E1。

图4为各类型转子电流对比图,其中Irc,a表示三相中波动最大的a相电流标幺值。计算各类型转子电流最大值的差值,结果如下:Ircm仿真值最大值为2.431,Ircm′仿真值最大值为2.172,Ircm计算值最大值为2.375,Ircm′计算值最大值为2.172,Ircm仿真值最大值与Ircm′仿真值差值ΔI1最大值为0.259,Ircm仿真值与计算值差值ΔI2的最大值为0.056,Ircm′仿真值与计算值差值ΔI3的最大值为0。

对比考虑恢复阶段与不考虑恢复阶段的仿真曲线可知,当考虑恢复阶段时,转子电流值要明显大于不考虑该阶段的曲线,差值ΔI1为0.259(标幺值),说明恢复阶段对高电压穿越性能产生了明显影响。仿真曲线与计算曲线相比,当都考虑恢复阶段时,对比图4和各类型转子电流最大值的差值计算值可以看出,两曲线转子电流最大值差距较小,差值ΔI2为0.056(标幺值),说明考虑恢复阶段的转子电流计算式较准确。从两条曲线的波动过程来看,在对称骤升故障开始阶段,计算值与仿真值相差较大,这是由于本文未考虑其他控制保护对定子磁链自由分量的抑制作用,导致了计算结果和仿真结果有较大的偏差;当都不考虑恢复阶段时,两曲线几乎重合,差值ΔI3为0,说明不考虑恢复阶段的转子电流计算式准确。

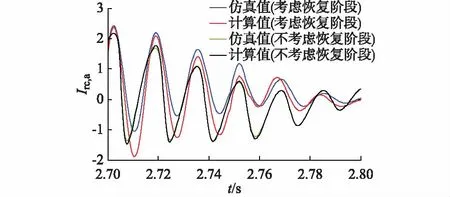
图4 各类型转子电流对比Fig.4 Comparison of various rotor currents

4.2 各故障参数对高电压穿越影响的仿真分析

在上节仿真条件下,通过控制变量分别改变不同的故障参数数值进行仿真,得到了不同骤升幅度下的定、转子电流仿真最大值,并与图3的计算值进行比较,结果如图5所示,图中实线与虚线分别表示仿真值与计算值。

图5(a)是在默认参数条件下,以不同的间隔时间Tr为控制变量,得到定、转子电流最大值的仿真值,并与图3的计算值进行对比。由图5(a)可知,随着间隔时间的增大,仿真值也随之减小,与图3(a)中计算值的趋势相同,并且在不同的间隔时间曲线中,定、转子电流计算值与仿真值的曲线几乎重合,误差较小,验证了上述理论分析的正确性,说明了考虑恢复阶段时Tr对定、转子电流影响的合理性。在Tr=8 s时的仿真曲线与不考虑恢复阶段的仿真曲线几乎重合,这也验证了当Tr≥8τs时,定子磁链自由分量已衰减完毕,不需考虑恢复阶段影响的结论。

图5(b)、(c)和(d)分别是以骤降深度p、故障角θ和转差率s为控制变量,得到不同变量下定、转子电流最大值的仿真曲线,并与计算值进行对比。由图5(b)、(c)和(d)的定、转子电流仿真曲线与计算曲线对比图可以看出,在不同的p,θ,s下,仿真曲线与计算曲线趋势走向相同,误差较小,验证了理论分析的正确性,说明了考虑恢复阶段时p,θ,s对定、转子电流影响的合理性。同时,由不考虑恢复阶段仿真曲线与其对应的计算曲线对比可知,当不考虑恢复阶段时,本文所建立的模型依然可以使用,扩大了本文模型的适用范围。

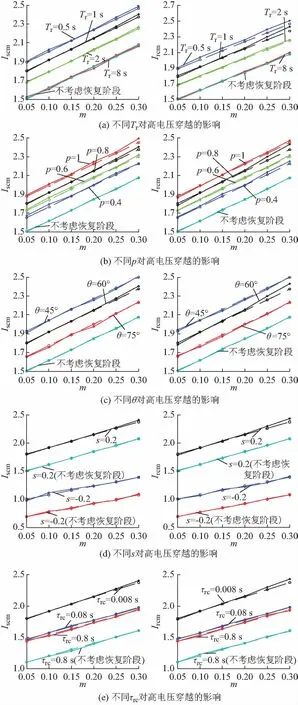
图5 不同故障参数下的定、转子电流最大值仿真值与计算值对比Fig.5 Comparison between simulated and calculated values of maximum stator or rotor current with different fault parameters

图5(e)是以不同的暂态转子时间常数为控制变量,得到定、转子电流最大值的仿真值,并与计算值进行对比。由图5(e)中两曲线的对比可以看出,两曲线误差较小,也说明了考虑恢复阶段的合理性。同时可知,暂态转子时间常数的改变对定、转子电流有较大的影响。暂态转子时间常数是随着Crowbar电阻的改变而变化的,因此若合理选择Crowbar电阻将会使定、转子电流快速下降,进而快速优化定、转子过电流现象。

5 结语

本文从双馈风电机组连锁脱网实际工况出发,考虑了电网电压骤降恢复阶段,剖析了风电场发生骤升故障的原因,详细论证了骤降恢复阶段的定子磁链自由分量对骤升故障穿越性能的影响。建立了考虑电网电压恢复阶段的双馈风电机组暂态模型，以定子磁链自由分量为切入点,对双馈风电机组动态特性进行了详细分析,得到了考虑恢复阶段的定、转子电流表达式,并进一步得到了考虑恢复阶段影响时的定子磁链自由分量大小比不考虑该阶段时增加了1倍多的结论。分析了各故障参数对骤升故障穿越性能的影响,其影响程度为θ>Tr>p>τr>s,同时得到了Tr≥8τs时即可不考虑恢复阶段对骤升故障阶段影响的结论。通过仿真分析,证明了本文推导的定、转子电流表达式有较好的准确性,验证了本文提出的计算公式和暂态模型的合理性和可行性。

本文也存在不足之处,如在理论推导过程中未考虑电网不对称故障的情况,在第二阶段高电压穿越过程中未考虑Crowbar电阻最优取值问题,使本文结论应用有一定局限,因此下一步研究将考虑电网不对称故障和Crowbar最优取值等方面。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

周步祥(1965—),男,博士,教授,主要研究方向:电力系统电网规划、调度自动化及计算机信息处理。E-mail： hiway_scu@126.com

董 申(1992—),男,通信作者,硕士研究生,主要研究方向:风电故障分析、调度自动化及计算机信息处理。E-mail: dongshen945@163.com

林 楠(1973—),女,工程师,主要研究方向:电力系统电网规划。