有源配电网的安全距离与安全分析方法

2018-09-18林启思

电力系统自动化 2018年17期

肖峻, 林启思, 左磊, 周欢

(智能电网教育部重点实验室(天津大学), 天津市 300072)

0 引言

配电网安全分析传统方法是基于N-1仿真得到安全信息[1-2]。安全域描述了电网满足安全约束的运行范围[3]。工作点(系统状态)到安全域边界的距离称为安全距离,安全距离于电网运行具有重要意义[4-5]。

安全距离的概念源于输电网,在输电网安全分析中,通过计算域中一个注入点与边界面的距离,从而给出系统的安全裕量[6]。安全距离已应用于配电网规划和运行相关领域[7-9]。文献[10]提出了配电网安全距离的定义,将安全距离分为几何安全距离(geometric security distance,GSD)与馈线安全距离(feeder security distance,FSD)。GSD定义为工作点到某个有效安全边界的垂直距离,代表多个负荷同时变化时的负荷裕度;FSD是工作点沿轴向到有效安全边界的距离大小,代表仅单个负荷变化时的负荷裕度。基于文献[10]的安全距离定义能够实现对某个工作点的安全评价:安全距离为正,表示工作点位于安全域内,工作点安全,反之不安全。安全距离大小体现了安全裕度。

本文发现文献[10]中定义还存在一些需要完善之处:①针对传统配电网,还需扩展到含分布式电源(distributed generation,DG)的有源配电网;②GSD和FSD是几何空间上的工作点位移,而工作点状态量变化并没有完整反映出来;③GSD和FSD有时无法与边界相交,原因是其他安全边界或状态空间边界的遮挡;④没有区分安全边界和状态空间边界,工作点可以穿越安全边界,但是不可能穿越状态空间边界。

针对上述问题,本文对安全距离进行重定义,建立了较完整的安全距离概念族,并扩展到有源配电网。最后,基于安全距离开展了以工作点越界分析为核心的安全分析,较全面展示了安全距离的用途。

1 有源配电网的安全距离

本节相关距离定义不仅适用于有源配电网,在传统配电网及未来考虑分布式储能元件、主动负荷、柔性装置的智能配电网中也同样适用。

1.1 有源配电网安全边界

安全距离计算需要基于有源配电网的安全域模型,故先介绍文献[11]提出的全象限安全域(TQSR)模型如式(1)至式(4)所示,目标函数为:

ΩTQSR=

{W=[PL1,PL2,…,PLm,PDG1,PDG2,…,PDGn]∈

Θ}

(1)

式中:ΩTQSR为有源配电网安全域;W为工作点;Θ为状态空间;PLm为负荷Lm的功率;PDGn为分布式电源DGn的出力;m和n分别为负荷和DG数量。

约束条件如下所示。

1)状态空间范围约束

(2)

式中:PLi为负荷Li功率;PLi,max为其功率上限;PDGi为分布式电源DGi出力;PDGi,max为其出力上限。

2)正常运行约束

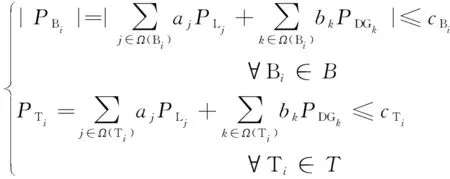
(3)

式中:PBi为线路Bi的功率;Ω(Bi)为Bi下游所有节点的集合;cBi为Bi的容量;B为线路的集合;PTi为主变压器Ti的功率;Ω(Ti)为Ti下游所有节点的集合;cTi为Ti的额定容量;T为所有主变压器的集合;PLj为负荷Lj功率;PDGk为DGk功率;aj和bk分别为负荷和DG系数。

3)N-1安全约束

(4)

式中:ψk为元件，∀ψk∈Ψ，Ψ为故障集。因线路存在双向潮流,故安全域表达式存在绝对值符号[11]。

本文沿用文献[10]的直流潮流模型,原因为[11]:城市配电线路不长、网损较小[12];电网和DG均具备调压能力,电压不难保持在规定范围内。文献[13]建立了交流潮流安全域模型,与直流潮流比较发现,在城网中二者误差不大,可采用直流潮流模型[13]。

将式(3)和式(4)取等号时就构成安全边界βi,表达式为[14]:

(5)

式中:PB为βi上任意点;PLBj和PDGBk分别为PB中位于Bi或Ti下游节点的负荷功率和DG出力;aBj和bBk分别为其相应系数;R∈{cBi,cTi},“±”是在去掉式(3)和式(4)中绝对值符号时引入的，当取“+”时,βi为正向潮流边界，若取“-”,则βi为反向潮流边界。

1.2 安全距离的定义

1.2.1几何距离与状态距离

将任意两个工作点间的距离分为两类:①几何距离,工作点从一个位置a运动到另一位置b的空间几何距离，即欧式距离;②状态距离,工作点从一个位置a运动到另一位置b时系统状态的变化量,等于各变量变化量绝对值之和,即曼哈顿距离[15]。曼哈顿距离常用于城市网格状道路中最短路径求解。

假设P是N维空间中的工作点,P从位置a运动到位置b的几何、状态距离记作DGD,ab和DSD,ab,计算公式为:

(6)

(7)

式中:Pi,a和Pi,b分别为工作点P位于a,b时的状态量。

在运行中,状态距离更为重要,原因如下。

1)几何距离是空间几何距离,系统状态空间是一个虚拟空间,工作点并不能真正沿空间距离的轨迹到达另一点,真正引起工作点到达另一点的是系统状态变化。例如,若要控制一个不安全点回到安全状态,需降低部分节点的负荷功率,各负荷功率变化绝对值之和是一种代价,状态距离准确反映了这种代价。

2)从应用角度,几何距离具有相对性,不具有绝对性;状态距离同时具有相对性和绝对性。相对性指两个距离值是可比的;绝对性指单个距离值就具有实际物理意义。因此单个几何距离不建议在实际配电网中使用,而单个状态距离则可以。

1.2.2几何安全距离与状态安全距离

安全距离定义为工作点在状态空间内沿某方向到达某安全边界的距离。若先碰到状态空间边界,则该安全距离为无穷大,表示不可能碰到该安全边界,沿该方向恒安全。

本文，安全距离也分为几何安全距离GSD和状态安全距离(state security distance,SSD)两类。本文中，GSD的物理意义是工作点到安全边界在空间上的欧式距离未必是垂直方向上的距离，与文献[10]不同;SSD的物理意义是工作点到安全边界的曼哈顿距离,即两工作点间各分量变化量的绝对值之和。当工作点安全时,SSD反映了一种安全裕度;当工作点不安全时,SSD反映了工作点回到安全边界的代价。

1.2.3最短/最长安全距离

相应地,有最长安全距离,分为最长几何安全距离(longest geometric security distance,LGSD)和最长状态安全距离(longest state security distance,LSSD)。LSSD对应至该边界的越界最安全方向(安全工作点)和最大控制代价方向(不安全工作点)。

1.2.4安全域最短/最长/平均安全距离

安全域最短几何安全距离(security region shortest geometric security distance,SR-SGSD)表示工作点到所有安全边界的最短几何距离,简称域最短几何距离;安全域最短状态安全距离(security region shortest state security distance,SR-SSSD)表示工作点到所有安全边界的最短状态距离,简称域最短状态距离,该距离对应方向为整个域最危险方向(安全工作点)和最快回到域内的方向,即最小控制代价方向(不安全工作点)。

相应地,也有域最长距离,分为域最长几何距离(security region longest geometric security distance,SR-LGSD)和域最长状态距离(security region longest state security distance,SR-LSSD)。SR-LSSD对应安全域的最安全方向(安全工作点)和最大控制代价方向(不安全工作点)。

安全域平均几何安全距离(security region mean geometric security distance,SR-MGSD)表示工作点到所有安全边界的SGSD平均值,简称域平均几何距离;安全域平均状态安全距离(security region mean state security distance,SR-MSSD)表示工作点到所有安全边界的SSSD平均值,简称域平均状态距离。SR-MSSD能反映工作点的综合安全程度,值越大,表示工作点越安全,反之越危险。

1.2.5垂向安全距离

文献[10]的GSD与FSD都属于几何距离范畴。文献[10]的GSD实际是工作点到斜线安全边界[16]在垂直方向上的距离,本文将其重定义为垂向几何安全距离(vertical geometric security distance,VGSD)。VGSD代表了当斜线边界所含元件功率同时变化时支路的安全裕度[17]。VGSD对应的状态距离为垂向状态安全距离VSSD。

需要指出,VGSD只对斜线边界有意义,目的是避免与后面的轴向安全距离重复。本文对斜线边界和直线边界进行更加严格的区分:安全边界在二维空间中的所有投影,仅能与坐标轴垂直的为直线边界,否则为斜线边界。现有斜线边界和直线边界都是二维平面上的[16]。

当沿垂向碰到斜线边界前先碰到状态空间边界,VGSD无穷大。当沿垂向只能到达该边界延长线时,VGSD不存在,如图1所示。当VGSD不存在或无穷大时,最接近垂向方向的几何距离最短。

良渚文化遗址的重要玉器玉琮与玉璧是祭天之物，特别是玉琮很可能兼有祭天与祭地两重功能，其地位之重要无可比拟。它是天地精神最切的概括、最佳的象征。良渚的玉琮造型极美，外方内圆。这方圆合体因暗合对立统一的规律，不仅在形式美上具有一种既整齐又灵动的美感，而且在内容上具有深邃的哲理，耐人寻味。从中国古代哲学来说，它让人想到阴阳、四象、八卦。

图1中,β1为斜线边界。VGSD只对β1有意义。工作点P能沿垂向越过β1,故其VGSD存在;P*沿垂向越过β1过程中会先碰到β2,故VGSD不存在。

图1 VGSD的概念Fig.1 Concept of VGSD

1.2.6轴向安全距离

工作点沿某个轴向到某安全边界的几何距离称为轴向几何安全距离(axial geometric security distance,AGSD),对应的状态距离为ASSD。ASSD总是与AGSD相等,原因是轴向只有一个变量变化,曼哈顿距离就等于几何距离。

需要指出,垂向安全距离针对斜线边界;轴向安全距离不区分直线边界和斜线边界。AGSD实际上指出了工作点至某直线边界的最短几何距离,但当直线边界部分被截断后工作点沿相应轴向率先到达其他边界时,会找到最接近轴向的方向使几何距离最短。

文献[10]的FSD与AGSD有一定区别,本文将FSD重新定义为安全域轴向几何安全距离(security region axial geometric security distance,SR-AGSD),简称域轴向几何距离,即工作点在状态空间内沿某个轴向出发碰到的第一个安全边界的几何距离。若先碰到状态空间边界,则该安全距离为无穷大,表示不可能碰到安全边界,沿该轴向恒安全。SR-AGSD反映和某个轴向相关负荷或DG的安全裕度,对应的状态距离为SR-ASSD。

图2中,P沿PL1轴向越界会先碰到状态空间边界(PL1容量边界),因此,SR-AGSD无穷大。P沿PL2轴向先碰到β1,PL2轴向的SR-AGSD就是β1的AGSD。β2的AGSD比β1的AGSD略长。

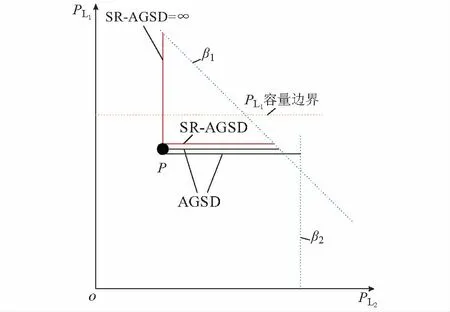
图2 SR-AGSD的概念Fig.2 Concept of SR-AGSD

1.2.7安全距离概念族

上述各安全距离定义的关系如图3所示。本文大大扩展了安全距离的概念,形成了更完整的安全距离概念族。现有安全距离是图3概念中2个距离,即文献[10]的GSD是本文中的VGSD,文献[10]的FSD是本文中的SR-AGSD。图中距离均含几何及状态距离。

图3 安全距离概念族Fig.3 Concept clan of security distance

1.3 安全距离的计算

文献[10]的方法因不能处理反向潮流边界而不适应有源配电网(详见附录A),本文进行了改进,并以SGSD的计算方法为例进行了说明。

1.3.1SGSD的计算方法

SGSD计算可转化为求解非线性规划问题:目标函数是工作点至某安全边界的最短几何距离;等式约束是该边界表达式;不等式约束是其余安全边界对应的约束;工作点分量上下限是状态空间约束。

已知工作点P(PL1,PL2,…,PLm,PDG1,PDG2,…,PDGn)和边界βi,P至βi的SGSD记为DSGSD,计算方法为:

(8)

式中:PLx和PDGy分别为工作点P的负荷功率及DG出力,ax和by分别为其系数;容量R前的“±”用于处理正向潮流和反向潮流,“±1”用于保证结果的正负能反映工作点在安全域的内外,βi为正向潮流边界时,上式中所有“±”取为“+”,反向潮流边界时均为“-”。

因此,式(8)既能计算正向潮流边界的距离,还能计算反向潮流边界的距离。此外,式(8)直接采用DG功率,而没有将其作为负的负荷归并到负荷功率中,该处理方式更清晰。

式(8)也适用于传统配电网,当式(8)略去DG分量且“±”取为“+”时,便退化成传统配电网公式,即

(9)

式中:ΩDSSR为传统配电网安全域。

1.3.2LGSD的计算方法

将式(8)的目标函数修改为工作点至某一安全边界的最长几何距离,得到LGSD计算公式为:

(10)

式中:DLGSD为工作点的LGSD。

1.3.3SSSD/LSSD的计算方法

将式(8)和式(10)的目标函数修改为状态距离,便可得到式(11)中SSSD/LSSD计算公式。其中,DSSSD和DLSSD分别为工作点的SSSD和LSSD。

(11)

1.3.4安全域平均安全距离计算方法

(12)

(13)

式中:DSR-MGSD和DSR-MSSD分别为工作点的SR-MGSD和SR-MSSD;DSGSD,βi和DSSSD,βi分别为工作点至边界βi的最短几何及状态安全距离;m0为边界个数。

1.3.5安全域最短/最长安全距离计算方法

通过比较所求工作点至所有安全边界的SGSD,LGSD,SSSD,LSSD的大小,可以得到SR-SGSD,SR-LGSD,SR-SSSD,SR-LSSD,具体如下。

对于安全工作点,SR-SGSD/SR-SSSD是工作点至所有安全边界SGSD/SSSD中的最小值;SR-LGSD/SR-LSSD是至所有安全边界LGSD/LSSD中的最大值;对于不安全工作点,SR-SGSD/SR-SSSD是所有负值SGSD/SSSD中最小值;SR-LGSD/SR-LSSD是所有负值LGSD/LSSD中最大值(不计符号)。

1.3.6垂向安全距离计算方法

当βi为斜线边界时,若式(8)所求安全距离垂直于βi,则该距离为VGSD。判断所求安全距离是否垂直于βi步骤如下。

1)用式(8)求出距离及工作点位移,即工作点各分量变化量构成的向量,记作ΔP=[ΔPL1,ΔPL2，…,ΔPLm,ΔPDG1,ΔPDG2,…,ΔPDGn]。

3)判断ΔP与nβi是否平行,若平行则所求距离为VGSD,否则βi被其他边界遮挡,此时需进一步判断遮挡βi的边界类型,若是状态空间边界,则VGSD取无穷大;若是安全边界,则VGSD不存在。相应的VSSD求法同式(7),且符号与VGSD相同。

1.3.7轴向安全距离计算方法

P沿PLi和PDGi轴向至边界βi的AGSD记作DAGSD,求法如式(14)所示。

(14)

式中:K∈{ai,bi},为边界表达式中PLi和PDGi的系数。

1.3.8域轴向距离计算方法

为了方便SR-AGSD的计算, SR-AGSD可以分为工作点沿正轴向(负荷功率增加和DG出力减少方向)至所有正向潮流边界的最短距离SR-AGSD+及工作点沿负轴向(负荷功率减少和DG出力增大方向)至所有反向潮流边界的最短距离SR-AGSD-。

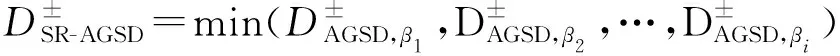
(15)

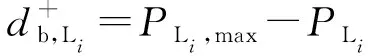
(16)

(17)

(18)

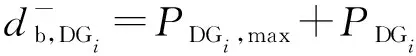
(19)

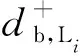
工作点沿PLi和PDGi轴向的SR-AGSD计算步骤见附录B图B1。相比于传统方法,本文方法更为细致,考虑到状态空间边界的遮挡导致SR-AGSD无穷大及不安全工作点出现SR-AGSD不存在的情况。SR-ASSD求法同式(7),且符号与SR-AGSD相同。

1.4 本文概念和算法的优势

相对现有安全距离概念及算法,本文更具如下优势。

1)本文扩展了安全距离的概念及计算方法,所提状态距离更适用于配电网安全分析。

2)最短/最长安全距离可以反映安全工作点的最小/最大安全裕度和最危险/最安全方向及不安全工作点最小/最大控制代价方向。

3)安全域平均安全距离可以反映工作点安全程度。

4)本文方法由于能处理反向潮流边界,因此除传统配电网外,还能适用于含DG有源配电网,而传统方法只能适用于传统配电网。

5)本文方法还考虑了其他边界遮挡导致安全距离不存在或无穷大的情况。

2 基于安全距离的安全分析

传统安全分析首先判断工作点是否安全,然后分析安全或不安全程度,本文增加了越界分析。

2.1 安全性判断

与传统配电网相同,有源配电网的安全性也是依据工作点在安全域内外来判断。本文定义的安全距离具有正负,反映了工作点在域内外的不同,当所有安全距离均为正值时,工作点安全;若存在安全距离为负值,工作点不安全。

2.2 安全程度分析

除是否安全外,还需要评价工作点安全程度。本文采用域平均状态距离SR-MSSD来反映工作点的综合安全程度,SR-MSSD越大,工作点安全程度越高,越安全,反之越危险。

另外,当工作点安全时,再采用SR-SSSD来反映工作点从安全到不安全最危险方向和距离。

2.3 越界方向分析

有源配电网工作点的越界模式比传统配电网更为复杂,且DG出力具有间歇性和不确定性的特点,使得工作点更易越界。

按相对安全边界的方向将越界分为垂向越界、轴向越界和其他方向越界三种模式:①垂向越界定义为工作点沿垂向至各斜线边界的越界方式;②轴向越界定义为工作点沿轴向至某安全边界的越界方式;③其他方向越界定义为工作点沿非垂向和非轴向至安全边界的越界方式。

2.4 正向与反向越界

1)正向越界

正向越界定义为工作点不满足正向潮流约束而越过正向潮流边界。传统配电网中,由于N-1约束比正常运行(N-0)约束更严格,故正向潮流边界仅包含N-1安全边界。而有源配电网中,N-1边界未必比N-0边界严格,边界必须同时包含N-0边界和N-1边界。

2)反向越界

反向越界定义为工作点不满足反向潮流约束而越过反向潮流边界。有源配电网中,反向潮流边界包含N-0边界和N-1边界,工作点能反向越界;而传统配电网无反向潮流边界,工作点无反向越界模式。

为避免反向越界,配电网设计时一般遵循DG总容量小于馈线出口容量的原则,从而使馈线出口容量总能大于反向潮流[11,18-19]。

3 算例分析

先采用文献[11]中简单有源配电网展示本文概念和方法,再基于IEEE-RBTS-BUS4[20]算例进一步验证。

3.1 算例基本情况

采用文献[11]中简单有源配电网,如图4所示。

图4 有源配电网
Fig.4 Active distribution network

在此算例中,设线路容量1 MVA,负荷功率范围为[0,1.5]MVA。为研究高比例DG的接入问题,扩大DG出力范围为[-1,0]MVA。

3.2 安全边界计算结果

列写出该算例的状态空间约束和安全约束,得到安全域的表达式,见附录C表C1。将约束取等并剔除无效边界后得到安全边界如下。

N-0:β1+PL2=1 MVA

(15)

(16)

式中：β1+,β2+,β3+为正向潮流边界;β4-为反向潮流边界。安全边界由N-0和N-1安全边界组成。其中，β1+和β2+为直线边界;β3+和β4-为斜线边界。需要注意,每一个取等号的边界,还必须满足在安全域内,即满足其他所有不等式。

状态空间约束取等后得到如下状态空间边界如下。

PDG1:下边界PDG1=-1 MVA,上边界PDG1=0 MVA。

PL2:下边界PL2=0 MVA,上边界PL2=1.5 MVA。

PDG3:下边界PDG3=-1 MVA,上边界PDG3=0 MVA。

PL4:下边界PL4=0 MVA,上边界PL4=1.5 MVA。

3.3 工作点安全分析

取工作点P1:PDG1=-0.8 MVA,PL2=0.2 MVA,PDG3=-0.2 MVA,PL4=0.2 MVA。

3.3.1安全性判断

利用式(8)、式(10)、式(11)、式(14)求得P1到各安全边界的距离,所有安全距离均为正值,因此P1安全。对P1进行N-0和N-1仿真校验,校验结果说明P1安全,证明了用安全距离符号判断安全性的正确性。

3.3.2越界分析

对P1逐个安全边界进行越界分析,结果如表1所示。P1越过β1+,β2+,β3+为正向越界,越过β4-为反向越界。以P1越过β2+,β4-为例,采用二维可视化方法观察P1越界模式。

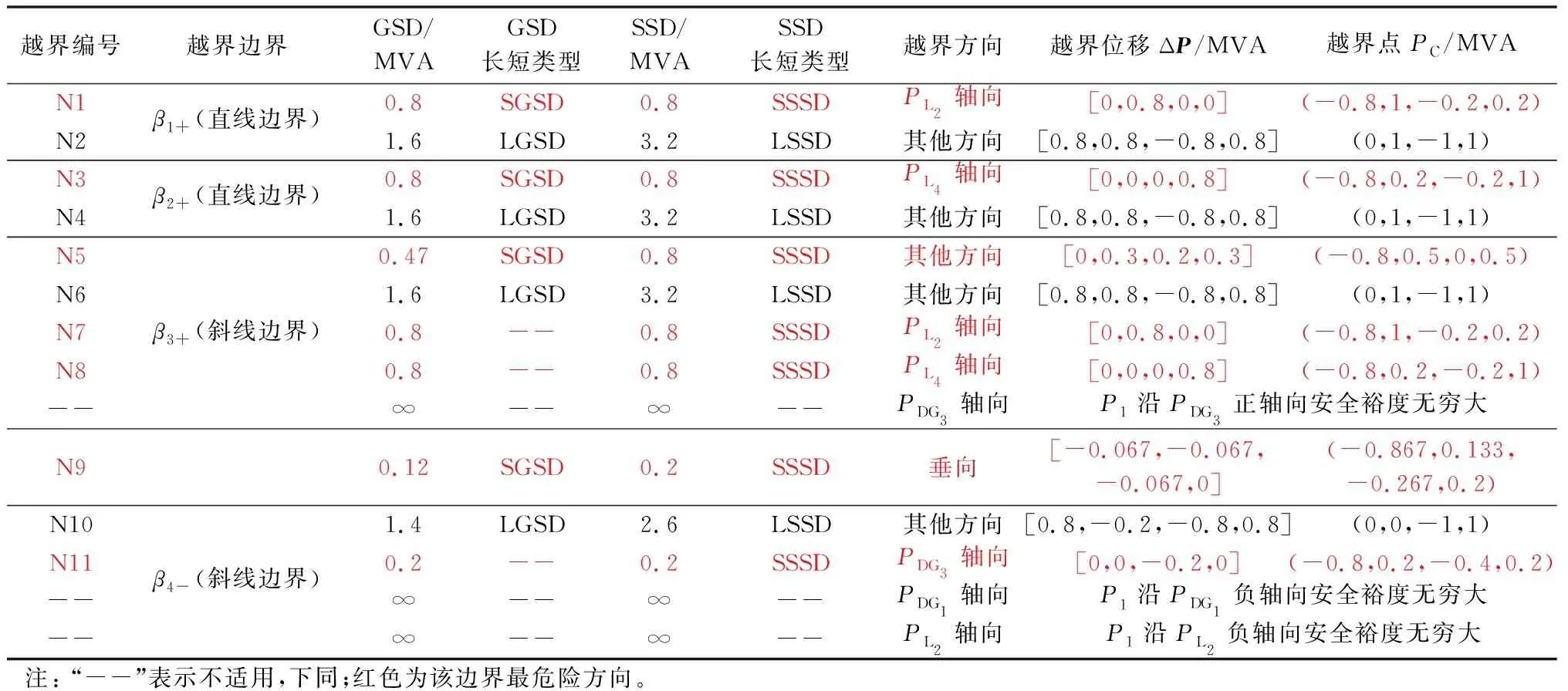
表1 P1到各安全边界的距离和越界数据Table 1 Data of distance and crossing boundaries from P1 to security boundaries

3.3.2.1P1至β2+越界分析

选取PDG1和PL4为观测变量,固定PL2=0.2 MVA,PDG3=-0.2 MVA,观察P1沿各方向越过β2+,见图5。

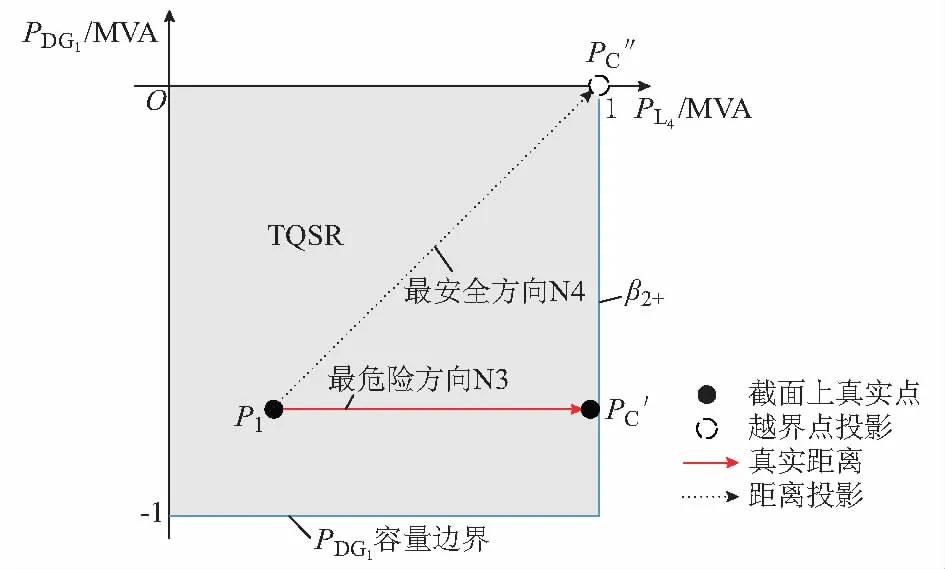
图5 P1至β2+越界Fig.5 Crossing boundary from P1 to β2+

1)最短距离/轴向越界

图5中,当L4增加0.8 MVA时,P1沿PL4轴向运行至β2+,越界点为PC′(-0.8,0.2,-0.2,1)(单位为MVA,下同)。该方向距离最短且几何距离和状态距离相等,AGSD=ASSD=0.8 MVA。该方向到边界β2+是最危险的方向。

2)最长距离

P1运行至β2+最安全方向是到PC″(0,1,-1,1)(单位为MVA,下同)方向,该方向裕度最大为3.2 MVA。P1到越界点位移为(0.8,0.8,-0.8,0.8)。因PC″的PL2≠0.2 MVA,PDG3≠-0.2 MVA,故其不在该截面上,图5中用虚线点表示。

3.3.2.2P1至β4-越界分析

选取PDG1和PDG3为观测变量,固定PL2=PL4=0.2 MVA,观察P1越过β4-,如图6所示。

1)最短距离/垂向越界

经式(11)求解,P1运行至β4-的SSSD为0.2 MVA。运行中的物理意义如下。

P1经过位移ΔP=[-0.067,-0.067,-0.067,0](单位为MVA,下同)后到达安全边界β4-,越界点为PC′(-0.867,0.133,-0.267,0.2)。

SSSD为0.2(=0.067+0.067+0.067)MVA,即DG1增加0.067 MVA至0.867 MVA,L2减少0.067 MVA 至0.133 MVA,DG3增加0.067 MVA至0.267 MVA,L4不变。

由于状态安全距离最短,因此该方向是P1运动到β4-最危险的方向。

此外,β4-法向量nβ4-=[1,1,1,0],ΔP与nβ4-

平行,说明该越界方向是β4-的垂向。

2)轴向越界

当DG3增加0.2 MVA时,P1沿PDG3轴向运行至β4-,越界点为PC″(-0.8,0.2,-0.4,0.2),轴向距离AGSD与ASSD相等为0.2 MVA。

图6 P1至β4-越界Fig.6 Crossing boundary from P1 to β4-

观察图6,P1至β4-上被PDG1及PDG3轴向所截线段各点越界时对应SSD相同且最小,但仅垂直方向能使GSD最小,越界编号N9和N11为最危险的方向，N10为最安全的方向。

3)最长距离

P1运行至β4-最安全方向是到越界点PC‴(0,0,-1,1)的方向,该方向裕度最大,为2.6 MVA。P1到越界点位移为(0.8,-0.2,-0.8,0.8)。PC′和PC‴不在该截面上,故图6用虚线点表示。

3.3.2.3 单安全边界越界总结

1)对于直线边界,其对应的轴向是最危险方向,方向越偏离轴向,GSD和SSD越大;当轴向不能越界时,最危险方向是最接近轴向的方向。

2)对于斜线边界,最危险方向是由与该边界相关轴向围成范围内的所有方向。当该范围被其他边界遮挡时需要进行一定修正(见附录C)。

3)对于直线边界,GSD与SSD呈正相关;对于斜线边界,GSD与SSD不呈正相关,所有使SSD最小的越界方向中仅垂向或最接近垂直的方向能使GSD最小,但GSD最大时SSD必最大。

3.3.3总体越界危险性排序

对表1中11个方向按SSD排序,得到表2。

表2 P1从整个安全域越界的危险性排序Table 2 Dangerousness order from P1 to crossing security region

由表2可知,在整个安全域中从P1出发。

1)最危险方向是编号N9和N11的越界方向,即β4-的垂向和PDG3轴向,只需使DG1和DG3均增加0.067 MVA、L2减少0.067 MVA或使DG3增加0.2 MVA时,P1就会越界,SR-SSSD=0.2 MVA。

2)最安全方向是编号N2,N4,N6的越界方向,只需使DG1减少0.8 MVA;L2,DG3,L4均增加0.8 MVA时,P1会同时越过边界β1+,β2+,β3+;越界点为三个边界的交点(0,1,-1,1)(单位为MVA,下同),SR-LSSD=3.2 MVA。

3)最长安全距离和最短安全距离差别显著,即有的方向非常危险,接近临界;有些方向则很安全,有较大裕度。

3.3.4域轴向距离

域轴向距离是仅单个变量变化时越界的最短距离。篇幅所限,正文不做介绍,结果见附录C表C2。

3.4 多工作点安全性综合比较

新增5个工作点P2至P6,数据见附录C表C3。对P1至P6求域最短/最长/平均状态距离,结果如表3所示。P1至P6到各安全边界距离详见附录C表C4。

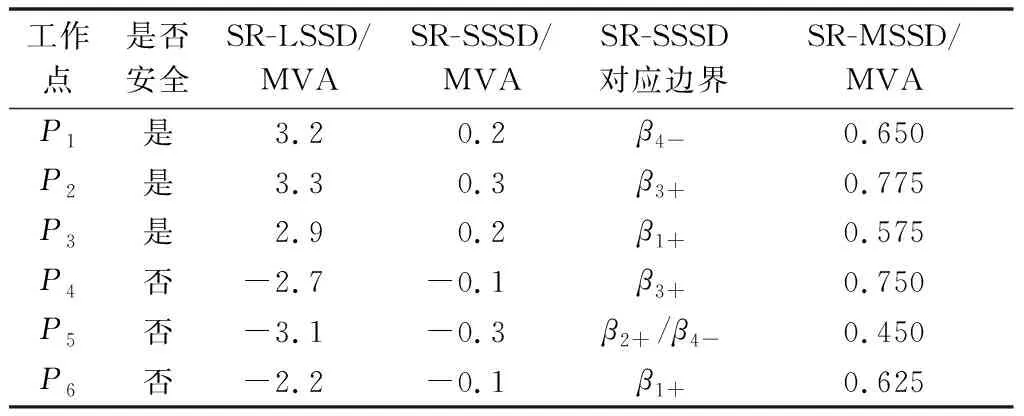
表3 P1至P6最短/最长/平均状态距离Table 3 Shortest/longest/mean state distance from P1 to P6

P1至P3安全,P2的SR-MSSD最大,因此最安全;P3的SR-MSSD最小,综合来看最危险,P3的L2增加0.2 MVA将越过直线边界β1+,是最危险的越界方向。

P4至P6不安全,P5的SR-MSSD最小,其不安全程度最高。分析P5回到域内的安全控制方案,P5到各边界的SSSD如表4所示。

表4 P5至各安全边界的SSSDTable 4 SSSD from P5 to security boundaries

如表4所示,P5位于边界β2+和β4-外,控制P5越过β2+和β4-回到安全的最小控制代价均为0.3 MVA。控制方案1为DG1减少0.1 MVA,L4减少0.2 MVA;控制方案2为L2增加0.1 MVA,L4减少0.2 MVA。两种控制方案实施后均能使P5安全。基于IEEE-RBTS-BUS4算例进一步验证了本文的概念及方法,具体结果详见附录D。