微网逆变器的VSG转动惯量和阻尼系数自适应控制
2018-09-18温春雪胡长斌朴政国周京华
温春雪, 陈 丹, 胡长斌, 朴政国, 周京华
(北京市电力电子与电气传动工程研究中心(北方工业大学), 北京市 100144)
0 引言
随着微网的快速发展,大量的电力电子设备融入传统电力系统中,电力电子设备低惯量、小阻尼的缺点成为微网领域关注的焦点,虚拟同步发电机(VSG)控制技术应运而生[1-3]。传统VSG参数固定的局限性,使得VSG的控制效果难以满足微网并离网运行要求,而将VSG与自适应控制结合,可以提高VSG的灵活性、可拓展性和可靠性[4]。
微网的运行状态分为离网和并网2种状态。离网工况下,逆变器输出频率不再由电网提供支撑,而是依靠下垂特性进行调节。故风电、光伏等新能源的间歇性和波动性的影响,以及不可预测的负载波动等都会对逆变器输出频率的动态特性造成影响,甚至难以保证其稳态特性良好[2]。并网工况下,逆变器输出频率由电网提供支撑,故根据VSG下垂特性,输出功率的动态特性与转动惯量和阻尼系数均有关,故当出现频率或者输入功率扰动时,逆变器输出功率会有超调或者振荡,甚至会有较大的功率冲击,导致过流保护。结合转子的机械方程可知,在动态过程中,转动惯量、阻尼系数、频率和输出功率间应该相互适应。
目前基于VSG的自适应控制策略大致有如下4种。
1)在VSG直流端利用分布式光伏与储能配合,构成光储联合系统,利用储能输出功率弥补光伏电源动态特性带来的不足[5-8]。但光伏电源动态特性复杂,较难控制和跟踪,并且这类系统直流侧仍然为储能电池,并没有从根源上解决问题。
2)自适应频率控制方法,根据电网频率的特性来决定VSG运行在并网发电状态、电网调频状态或者离网运行状态[9]。该方法考虑了电网频率变化对VSG输出频率的影响,忽略了VSG直流侧出力波动性对VSG输出的影响。
3)模拟二次调频原理,采用有功功率—频率下垂系数自适应控制方法[10],但该方法较难保证系统稳定性。
4)转动惯量自适应控制方法,根据VSG实际需求和数学关系,建立相应的约束条件或自适应转动惯量函数,根据动态变化自适应更改转动惯量[11-21]。
文献[11-14,17-18]着重考虑转动惯量的自适应问题,但在动态过程中,为达到较好的调节性能,不同转动惯量应该匹配不同的阻尼系数,因此阻尼系数作为VSG功率环的重要参数之一,也应该采用自适应控制,从而达到更优的调节性能。文献[15-16]同时提出了转动惯量和阻尼系数的自适应控制方法,但在调节过程中采用分区域判断的方法来确定转动惯量和阻尼系数的值,判断过程较为烦琐,缺乏灵活性。
本文在文献[13]构建的转动惯量与频率变化率间的函数关系式的基础上,根据VSG的功能表达式得出了转动惯量与VSG频率变化率的函数关系,同时根据转动惯量和阻尼系数之间的关系式,进一步得到了阻尼系数与频率变化率绝对值间的函数关系。根据函数关系式,设计出了自适应转动惯量和阻尼系数的控制结构图,并对该函数中涉及的参数进行了分析,总结出取值方法。本文建立的自适应函数控制的判断条件仅为频率变化率,可根据动态过程中输出频率的暂态波动引起的频率变化率的变化来动态地自适应调节转动惯量和阻尼系数的值,既保证了控制的有效性也体现了控制的灵活性。最后,利用MATLAB/Simulink仿真模型和VSG实验平台验证了本文所提自适应控制方法。
1 转动惯量和阻尼系数对系统动态响应的分析
根据VSG的基本原理,VSG的转子机械方程为:
(1)
式中:J为转动惯量;D为阻尼系数;Pref为输入功率;P为输出功率;Tm和Te分别为机械转矩和电磁转矩;ω和ω0分别为输出角频率和额定角频率;t为时间。
转动惯量可用惯性时间常数H衡量[12],即
(2)
式中:Sn为VSG的额定容量。
令ωr=(ω-ω0)/ω0,可得:
(3)
令VSG的额定容量为额定有功功率,即Sn=Pn,可得转矩的基准值为:
(4)
由式(3)和式(4)可将式(1)化简为式(6),即
(5)
(6)
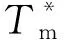
由式(6)可以得到如附录A图A1所示的VSG小信号分析模型。
如附录A图A1 所示,VSG的输入、输出功率响应特性是一个典型的二阶传递函数,即
(7)
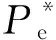
由式(7)得到自然振荡角频率ωn和阻尼比ξ分别为:
(8)
一般地,在阻尼Dp参数的整定过程中,可以利用“最优二阶系统”的概念,将系统的阻尼比定义在ξ=0.707 处[21-22]以获得较好的调节性能,即阻尼参数可选为:
(9)
则可得:
(10)
根据以上关系式,可做出有功环根轨迹图如图1所示。

图1 不同J和D下有功环的根轨迹Fig.1 Root locus with different J and D
从图1中J=0.2,0.5,1的情况下,D由1增大至100的根轨迹簇可以看出,s1和s2为系统的一对共轭复根,其变化轨迹如图1中箭头所示,箭头所指方向为D增加方向。当D较小时,s1和s2位于复平面右侧,即不稳定区域;随着D的增大,s1和s2变化到复平面左侧,系统动态特性较好,此时系统处于欠阻尼状态,有一定的超调;当D继续增大,s1和s2虚部逐渐为0,分别沿箭头所指方向移动到实轴上,并且沿相反方向运动,此时系统处于过阻尼状态,系统调节时间会增加。J=0.2时,D>10为过阻尼;J=0.5时,D>16为过阻尼;J=1时,D>22为过阻尼。且s1趋近于零点时,系统的稳定裕度减小。另外,随着J的增加,特征根s1和s2的分离点实部逐渐趋于0,即逐渐向虚轴移动,系统的响应速度变慢,并且随着J的增大,对应的阻尼不断减小,系统的动态性能及稳定性变差,故J不能超过1。实际运用当中,为保证可靠性,J一般限制在0.8以内。
结合式(1)所示的转子机械方程可知,在VSG的动态响应过程中,为达到较好的响应特性,应该需要转动惯量、阻尼系数、频率和功率间的相互适应。离网工况下,控制的目标为使输出频率达到较好的动态响应特性,并保证良好的稳态性能;并网工况下,控制目标为使输出功率达到较好的动态响应特性,并保证良好的稳态性能。
2 自适应模型的建立及分析
由式(1)忽略阻尼项变形可得:
(11)
由式(11)可知当功率缺额一定时,角频率的变化率与转动惯量成反比,进而可得频率变化率与转动惯量成反比,即
(12)
由式(12)可知,理论上当系统受到扰动,J设置越大,df/dt就越小,对频率的波动抑制就越有利,但根据上述根轨迹分析,以及逆变系统本身的物理限制,转动惯量不能设置太大,过大的转动惯量会造成系统动态特性变差,甚至不稳定。据此,转动惯量的设置可以根据暂态过程中频率的变化率来灵活地改变,保证df/dt变化较大时,J值能够及时快速变化。考虑到控制目的以及指数函数曲线的变化特点,本文以指数函数为基础建立关于J的自适应函数式。
由式(12)的关系式可以建立转动惯量和频率变化率间的函数式,并根据文献[13]所述关系式得:
(13)
式中:J0为稳态运行下的转动惯量;N为设定的频率变化率的临界值;k1和m1为函数式的系数。
在式(13)的基础上,进一步得到阻尼系数和频率变化率间的函数关系式。由式(2)、式(5)、式(8)可得:
(14)
令常数C=4ξ2SE/ω0,则
(15)
当|df/dt| (16) 则 (17) 当|df/dt|≥N时,由式(13)、式(15)、式(17)可得: (18) 由式(16)和式(18)可得阻尼系数和频率变化率间的函数关系式为: (19) 由式(19)可知,阻尼系数的取值也可用与系数k1和m1有关的表达式进行表述,其取值的规则由频率变化率来决定。 通过阈值N的设定可以减少转动惯量和阻尼系数的变化次数,保证系统稳态运行时不受影响。当|df/dt|较小,未超过N时,保持转动惯量和阻尼系数的值不变;当|df/dt|变化较大,超出了N时,则|df/dt|越大,J和D越大,通过改变J和D来改变VSG的输入端功率大小,进而抑制VSG输出频率的变化幅度,提高系统的暂态性能。 由式(1)可得: (20) 式中:ΔP为功率扰动;Δf为频率偏差。 由式(13)、式(19)、式(20)可得: (21) 由式(21)可知,N值与暂态时的J和D、系统允许的频率偏差Δf和功率扰动ΔP均有关。由式(13)和指数函数特性可得附录A图A2的分析曲线。 由图A2可知,m1>0,故满足要求的曲线均为位于第1象限的曲线。在N满足0 在选择系数k1时应考虑分布式电源的额定功率及整个系统允许的最大频率偏差值[13],由式(13)可得: (22) 由式(11)可得: (23) 式中:Δω为角频率偏差量。 由式(22)和式(23)可得k1的表达式为: (24) 将式(13)中J0和N均设为0,并根据式(19),将D0设为15,J0设为0.2,分别做出4组不同m1下转动惯量J随系数k1和频率变化率|df/dt|变化的三维曲线图和阻尼系数D随系数k1和频率变化率|df/dt|变化的三维曲线图,见附录A图A3和图A4。 由图A3和图A4可以看出,在|df/dt|较小时,转动惯量和阻尼系数的数值范围较小;当|df/dt|继续增大时,转动惯量和阻尼系数的数值变化逐渐加快。当m1由小变大时,三维曲面由凸变凹,说明在k1一定的情况下,增加m1会使得转动惯量和阻尼系数对频率变化率的变化更加敏感。故当m1较大时,在负荷突变的情况下,随着|df/dt|的增大,J和D增长迅速。因此在选择参数时,可以根据附录A图A3和图A4的4种典型情况,先选择m1的值,再根据系统的要求和VSG逆变系统本身的容量等限制对k1的值进行选择。 由以上分析可以得到自适应转动惯量和阻尼系数函数中,函数系数的确定规则如下。 1)k1的选择主要与系统允许的最大频率偏差和最大容量限制有关。 2)m1主要影响在不同的|df/dt|下,转动惯量和阻尼系数的变化趋势,在设计时可先行考虑。 在选择k1和m1时,应该综合考虑各影响因素,得到较优的自适应函数式,从而在保证系统稳定的情况下,尽可能地减小在暂态过程中输出频率和功率的变化幅值以及调节时间。 由式(13)和式(19)可得自适应VSG功率控制框图如图2所示。图2中,Kp为有功功率—频率下垂系数,LPF为低通滤波器,作用是滤除高频信号的影响。SD和SJ分别为J和D的限幅环节。 图2 自适应VSG功率控制框图Fig.2 Block diagram of VSG power control 为了验证转动惯量J和阻尼系数D对系统响应过程的理论分析,以及本文所提微网运行工况下自适应转动惯量和阻尼系数控制的正确性和有效性,在MATLAB/Simulink中建立了20 kVA的VSG模型,并搭建了相应容量的VSG实验平台,实验平台如附录A图A5所示。 直流源Udc=800 V模拟分布式电源,滤波电感L=3 mH,滤波电容C=15 μF,负载20 kW。根据第2小节的参数分析,k1=2.5,m1=2。阈值N选定为1.5,根据VSG稳态要求J0=0.2,D0=15,根据式(13)和式(19)可得: (25) (26) 图3为离网状态下,负载扰动时,|df/dt|,J,D和输出频率的仿真波形。在0.6 s时20 kW的负载突减14 kW,在相同情况下,分别进行了3组不同控制方式的仿真。 图3 离网状态下的仿真波形Fig.3 Simulation results under islanded condition J和D固定,采用普通VSG控制策略时,负载突变的情况下,输出频率有超调;当采用固定D,自适应调节J时,输出频率的超调有所抑制,但频率的衰减速度仍较慢,频率幅值仍有较小的波动;J和D均自适应调节时,能够保证输出频率无超调,由于在频率变化率达到0前,由式(26)计算增加了相应的D,因此频率在动态过程中的衰减速度增加了,并对频率的波动幅度有所抑制,体现了转子机械方程式(1)中,转动惯量、频率和阻尼系数间应该相互适应的过程。三种情况下,频率达到稳态值的时间一致,所以本文所提控制策略并没有增加调节时间,在频率变化率达到0时,及时将J和D切换为较小值。并且在VSG启动瞬间三种情况下的频率均有较小的波动,以及稳态时三者所达到的稳态值一定,可以看出,自适应控制策略中频率变化率的阈值设置合理,避免了转动惯量和阻尼系数在负载变化不大的情况下进行冗余的计算,从而影响稳态特性。同时,由图3(a)可以看出,J和D的值随着|df/dt|做动态变化,以达到适应的值,体现了本文控制方法的灵活性。 1)并网状态下输出功率仿真 图4为并网状态下,频率扰动和输入功率扰动时,|df/dt|,J,D和输出功率的仿真波形,图中对比了相同条件下,固定J和D与本文自适应J和D两种情况。0.6 s时切出预同步频率调节环造成频率扰动,1.2 s有功输入由0阶跃至8 kW造成输入功率扰动。由图4(b)可知,两种扰动情况下,固定J和D情况下,暂态性能较差;自适应J和D情况下,两种扰动下的暂态性能良好。 图4 并网状态下的仿真波形Fig.4 Simulation results under grid-connected condition 2)实验结果 图5、附录A图A6和图A7均为并网情况下,逆变器输出电流波形。附录A图A6所示的三种情况下功率给定均突增1 500 W,图A6(a)惯性阻尼较小时,暂态性能差,图A6(b)和(c)均无超调,但图A6(c)表现为过阻尼现象,调节时间长。附录A图A7所示的三种情况下功率给定均突增1 500 W,图A7(a)中,大阻尼作用时间较长,故调节时间较长;图A7(b)中,输出电流无超调,且调节时间合适;图A7(c)中,N值设置较大,导致自适应控制作用不及时,输出电流有一定的超调。图5为功率给定分别突增1 500 W和突减1 500 W时采用本文自适应J,D和固定J,D的对比,可知本文所提控制策略暂态性能较好。 图5 控制效果对比Fig.5 Comparison of control effect 本文在常规VSG控制算法的基础上,根据离网下负载扰动对频率的不利影响,并网下频率扰动和输入功率扰动对输出功率的不利影响,提出了自适应转动惯量和阻尼系数的控制策略,建立了自适应转动惯量和阻尼系数函数式,以此为基础设计出相应的控制结构图,并在MATLAB/Simulink和VSG实验平台上进行了仿真和实验验证,仿真和实验结果表明所提控制策略有效和正确。 本文的自适应控制策略目前只应用到了单台VSG逆变器上。在多机并联上,由于不同工况下所需要的阻尼系数和转动惯量会有所不同,如何通过自适应控制来更好地解决多机并联下功率环流和振荡,以及功率分配的问题,是本文工作今后需要进一步研究的内容。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 温春雪(1980—),男,博士,副教授,主要研究方向:微网运行及接口变换器控制。E-mail: wcx@ncut.edu.cn 陈 丹(1992—),女,通信作者,硕士研究生,主要研究方向:微网逆变器的VSG运行控制。E-mail: 2443180296@qq.com 胡长斌(1982—),男,博士,副教授,主要研究方向:微电网控制技术及智能电网协调控制。E-mail: changbinlove@163.com (编辑鲁尔姣)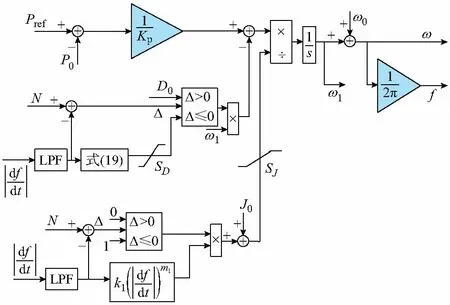
3 仿真和实验验证
3.1 离网状态下输出频率的控制仿真

3.2 并网状态下输出功率的控制仿真及实验


4 结语
