黄土的动变形特性及模型研究
2018-09-18,
,
(1.山西农业大学 城乡建设学院, 山西 晋中 030801;2.新南威尔士大学 土木与环境工程学院, 澳大利亚 悉尼 2052)
1 研究背景
黄土是广泛分布于我国西北和华北地区的一种区域性特殊土。原状黄土具有明显的结构性,其包含的大孔隙和欠压密结构使天然黄土在干燥条件下的强度较高,但是在遇水或者在地震等动荷载作用下,原生黄土的强度会急剧降低并伴随有较大的变形,这使得黄土具有湿陷性和震陷性这种明显区别于其他土类的特殊工程性质[1]。在我国,黄土广泛分布的西北和华北地区属于地震多发且烈度较高的地区,如甘肃、青海、宁夏大部分地区的抗震设防烈度均在7度以上,甘肃古浪的抗震设防烈度更是高达9度[2]。我国黄土分布区曾经发生过多次震级较大的地震,造成了大量的人身和财产损失[3-6]。随着西部大开发战略的实施,在黄土地区兴建各类建筑物已成为必不可少的选择,如高速公路、高速铁路、地下轨道、机场等。另外,我国黄土集中分布的中西部地区地震频繁发生且烈度较高,黄土地区因地震而导致的生命财产损失不可估量。因此,探究黄土在地震、交通等动荷载作用下的力学特性,为黄土地区的工程抗震设计提供强有力的理论支撑具有重要意义。
目前,基于黄土动力学课题的必要性,我国很多学者都曾致力于该方面的研究工作,并取得了大量的研究成果。其中,动模量和阻尼比作为反映黄土动力学性质的重要参数[7-8],得到了很多学者的关注和研究[9-11]。当黄土作为建筑物基础时,其动变形特性是决定上部建筑物在地震、交通等循环荷载作用下是否安全的重要工程性质。当前,学者对黄土动变形特性的研究包括黄土在循环荷载下的变形积累、黄土液化、黄土震陷等,并且也取得了大量的成果[12-15]。虽然我国学者在黄土动力特性的研究方面投入大量精力,并且该领域的很多理论也日趋成熟,但是目前对黄土动变形特性的很多研究还只停留在定性分析的层面上,关于定量地分析和预测黄土在循环荷载作用下的变形发展的研究成果并不多见。另外,考虑黄土的结构性并分析其动力压缩特性的研究也并未大量展开。基于此,本文利用SDT-20型双向动三轴仪同时对原状和重塑黄土进行试验研究,分析了黄土动变形发展的基本规律,并对比了原状结构性黄土和重塑黄土在动荷载作用下的压缩特性。最后提出了可以描述黄土在动荷载作用下变形发展的双曲模型,为黄土地基的动变形预测提供了一种可行的方法。
2 试验土样和试验方法
2.1 试验土样
本文试验所用土样是取自陕西杨凌某黄土边坡约6~7 m深处的Q3黄土。酒精燃烧法测得其天然含水率为18.2%,天然干密度为1.52 g/cm3,土粒相对密度为2.71,饱和条件下土体的含水率为28.8%,试验土体的其他主要物理性质指标见表1。经过标准击实试验,测得试验土体的最大干密度为1.703 g/cm3,最优含水率为19.3%。本文同时对原状和重塑黄土试样进行试验,试样均为实心圆柱形,试样的直径为39.1 mm, 试样高度为80 mm。

表1 试验土样的物理性质指标Table 1 Physical properties of test specimen
2.2 试验方法及内容
本文所有试验均在SDT-20型双向动三轴试验机上进行,包括在不同干密度、固结围压以及含水率下的重塑试样试验以及不同固结围压和含水率下的原状试样试验。基于对地震荷载作用短暂性的考虑,本文对所有试样均进行固结不排水剪切。待试样安装完毕后,先对试样进行等压固结,直至30 min内试样的轴向变形≤0.01 mm时,认为试样固结稳定。固结完毕后,在试样的轴向施加正弦波循环荷载进行剪切,荷载频率为1 Hz。试验过程中,轴向循环荷载的幅值逐级递增,每级荷载下振动10次,直至试样的轴向动应变达到5%认为试样发生破坏。结果分析时,选取每级循环荷载第5周次的数据进行。
3 试验结果分析
3.1 动剪切模量特性
土体在动荷载作用下的应力-应变关系具有明显的非线性和滞后性。动模量作为土体动力特性分析中的重要参数,可以很好地反映土体动应力-应变关系的非线性特性,而阻尼比则可以反应滞后性特性。土体的动剪切模量表征了其抵抗剪切变形的能力,土体的动剪切模量越大,剪切刚度也就越大。由本文采用的动三轴试验可以直接测得土体的动弹性模量Ed和动应变εd,利用式(1)、式(2)可以分别计算出动剪切模量Gd和动剪切应变γd:
Gd=Ed/[2(1+μ)] ;
(1)
γd=εd(1+μ) 。
(2)
式中μ为泊松比,考虑到试验土体为低液限黏土,取值为0.4。
图1表明,黄土动剪切模量随动剪应变的增大而逐渐减小。在动剪应变<1%时,动剪切模量随动剪应变的增大而急剧降低;当动剪应变>1%时,动剪切模量随动剪应变增大而减小的幅度逐渐降低,并最终趋近于一个稳定的水平。另外,黄土的剪切刚度随着干密度和固结压力的增大、含水率的降低,有不同程度的提高,这与之前学者得出的结论一致[9-10]。

图1 不同试验条件下黄土的Gd-γd关系曲线Fig.1 Gd-γd curves of loess in the presence of different test parameters
3.2 动变形累积特性
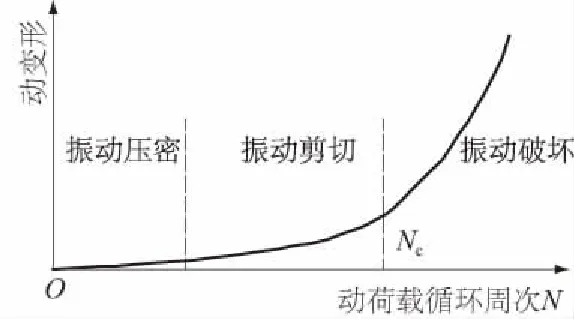
图2 典型的土体动应变累计曲线 Fig.2 Typical development curve of soil dynamic deformation
土体在动荷载作用下的变形会随着循环荷载的施加不断积累。谢定义[16]认为,土体受到动荷载作用时,如果动荷载的强度逐级增大,则土体一般会经历振动压密、振动剪切和振动破坏3个阶段,定义土体在循环荷载作用下,由振动剪切阶段向振动破坏阶段过渡时的循环周次为临界循环周次,用Nc表示,如图2所示。当土体受到的动荷载强度为一定值时,土体的动变形积累可能会发生2种情况:当动荷载的强度大于土体的临界动应力时,土体在动荷载的作用下动应变会不断积累并发生破坏;而当动荷载强度小于土体的临界动应力时,土体在动荷载作用下动应变增长较慢,并且动应变增长到一定值后会趋于稳定,此时土体不会发生破坏失稳。刘文化等[17]的研究也证实了这一点。
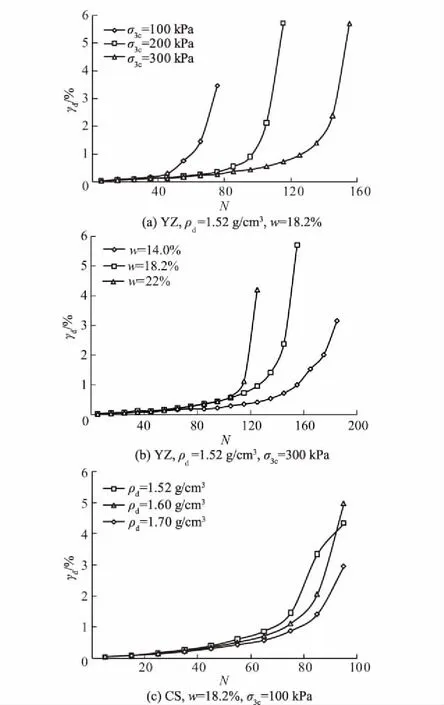
图3 不同试验条件下黄土的γd-N曲线Fig.3 Curves of γd-N of loess in the presence of different test parameters
3.2.1 动剪应变累计曲线
图3为黄土在动荷载作用下的动剪应变累积曲线,由于篇幅限制,文中只给出部分试验结果。图3表明,在本文施加的逐级增大动荷载作用下,黄土的动剪切应变发展均经历了振动压密、振动剪切以及振动破坏3个阶段。由图3(a)可以看出,随着固结围压的增大,黄土在相同循环周次下的动剪应变降低,黄土的动剪应变累积速率随固结围压的增大而明显降低,其在较高的固结围压下黄土能承受更多次数的循环荷载作用。图3(b)表明,黄土的动剪应变累积在较低的含水率下速度较慢,而在较高的含水率下速度加快,更加容易在动荷载作用下产生较高的应变而发生破坏。由图3(c)看出,重塑黄土的干密度越大,相同循环周次下黄土的动剪切应变越小,即黄土的干密度较大时,其在循环荷载作用下更加稳定。图3表明,随着固结围压和干密度的增大、含水率的减小,黄土的Nc值(见图2)明显增大,而Nc值越大,黄土经历振动压密和振动剪切阶段的历时越长,其承受动荷载作用的能力也越强。
3.2.2 动力压缩曲线
3.2.1节中分析了黄土在动荷载作用下的动剪应变累积曲线,是取每一级动荷载作用下第5周次的数据进行分析。利用每一级动荷载的所有循环的数据作出黄土的动剪应变累积曲线则如图4所示。

图4 黄土在循环荷载作用下的动剪应变累积曲线(所有级数)Fig.4 Accumulation of shear strain of loess under cyclic loading (including all cycles)
由图4可以看出,虽然黄土试样动剪应变的积累随着循环荷载的施加有明显的波动,但是总体呈现压缩变形逐渐增大的趋势。由于试样为非饱和土样,同时剪切结束时,试样的轴向双幅动应变不超过5%且并未发生明显的径向变形,因此,忽略试样在径向的变形,则可以利用实测的轴向动应变求出黄土试样在动荷载加载过程中的孔隙比,具体如式(3)所示。
其中,
V0=π(d0/2)2h0。
(4)
式中:e为试样的孔隙比;Gs为土粒相对密度,本文取值为2.71;ρd为试样的干密度,随着试样的压缩而逐渐增大;ρd0为试样的初始干密度,对于原状试样,为1.52 g/cm3;V0为试样的初始体积,具体的计算公式如式(4)所示;d0和h0分别为试样初始直径和初始高度,分别为3.91 cm和8 cm;εd为试样的轴向动应变,随着动荷载的施加逐渐增大。由于试样均为非饱和,虽然在压缩过程中试样的质量含水率保持不变,但是其体积含水率会不断增大,即试样的饱和度随着试样的压缩不断增大。
图5为土体在静态荷载作用下的e-lgP曲线。图5表明,由于原状土体天然结构性的存在,原状土的压缩曲线和重塑土有明显的差异。原状土的压缩曲线存在明显的拐点,并定义拐点处的压力为临界压力Pc。当P
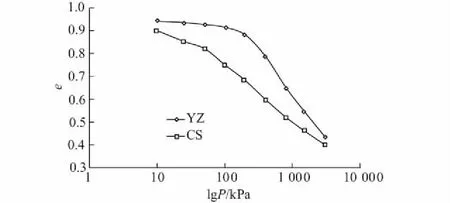
图5 典型的土体的静力压缩曲线(e-lgP)Fig.5 Curves of e-lgP of soils under static loading
利用式(3)计算出原状和重塑黄土在动荷载加载过程中的孔隙比,并作出原状和重塑黄土在动荷载作用下的压缩曲线,如图6所示。图6表明,和静力压缩不同,在动荷载作用下,原状和重塑黄土的压缩特性并没有明显的区别,二者的圧缩曲线均出现了明显的拐点。定义拐点处的动应力为临界动应力σdc。由图6可以看出:当σd<σdc时,原状和重塑黄土的孔隙比随动荷载的增大而缓慢减小,即在这个阶段,动应变的累积较慢;当σd>σdc时,原状和重塑黄土的孔隙比随着动荷载的增大急剧减小,动应变也在这个过程中迅速积累。当动荷载大于临界动荷载时,黄土试样的孔隙比会在很少的动荷载循环下迅速减少,土体会快速地发生形变而产生破坏。由图6可以看出,在动荷载加载过程中,原状和重塑黄土试样均可能发生应变软化。上述分析也表明,土体在静、动荷载作用下产生压缩变形的机理有明显的差异。
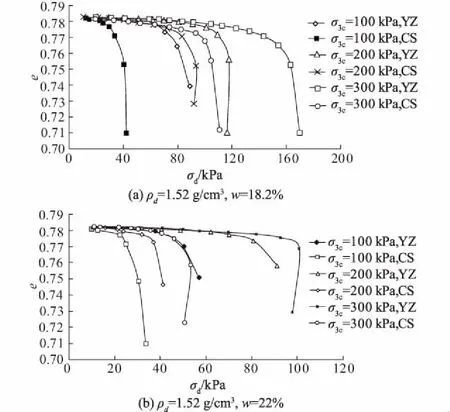
图6 黄土在动荷载作用下的圧缩曲线(e-σd)Fig.6 Curves of e-σd of loess under dynamic loading
3.2.3 动剪应变累计模型
由3.2.1节的分析可知,黄土在本文所施加的逐级增大的动荷载作用下,动剪应变随着动荷载的施加逐渐积累并达到破坏应变,与施加单一强度的动荷载作用明显不同。建立动剪应变积累和动荷载循环周次的函数关系,一方面可以预测土体在循环荷载作用下的耐久性,另一方面也可以预测土体在循环荷载作用下的动应变发展,这对工程抗震设计具有非常重要的意义。如图2所示,若把横轴(循环周次)和纵轴(动应变)调换位置后,发现动应变和动荷载循环周次呈现明显的双曲线关系,因此可以利用式(5)对动剪应变和循环周次的关系进行定量描述。
(5)
式中a,b为待拟合参数。
由式(5)可以得出
(6)
利用式(6)对黄土动剪应变和循环周次的关系进行描述,部分结果如图7所示。图7中,散点表示实测值,用T(Test)表示,实线表示计算值,用C(Calculation)表示。由图7可以看出,利用式(6)可以很好地预测动剪切应变随动荷载循环周次的变化趋势,但是在动剪应变较大时,预测效果会产生一定的偏差,但是在小应变范围内(<3%),本文所提出的双曲模型具有较好的适用性。利用式(6)所示的双曲模型表达式对本文试验所得的动剪应变-循环周次之间的关系进行描述,并使用差分进化法得出相应的模型参数值,如表2所示。
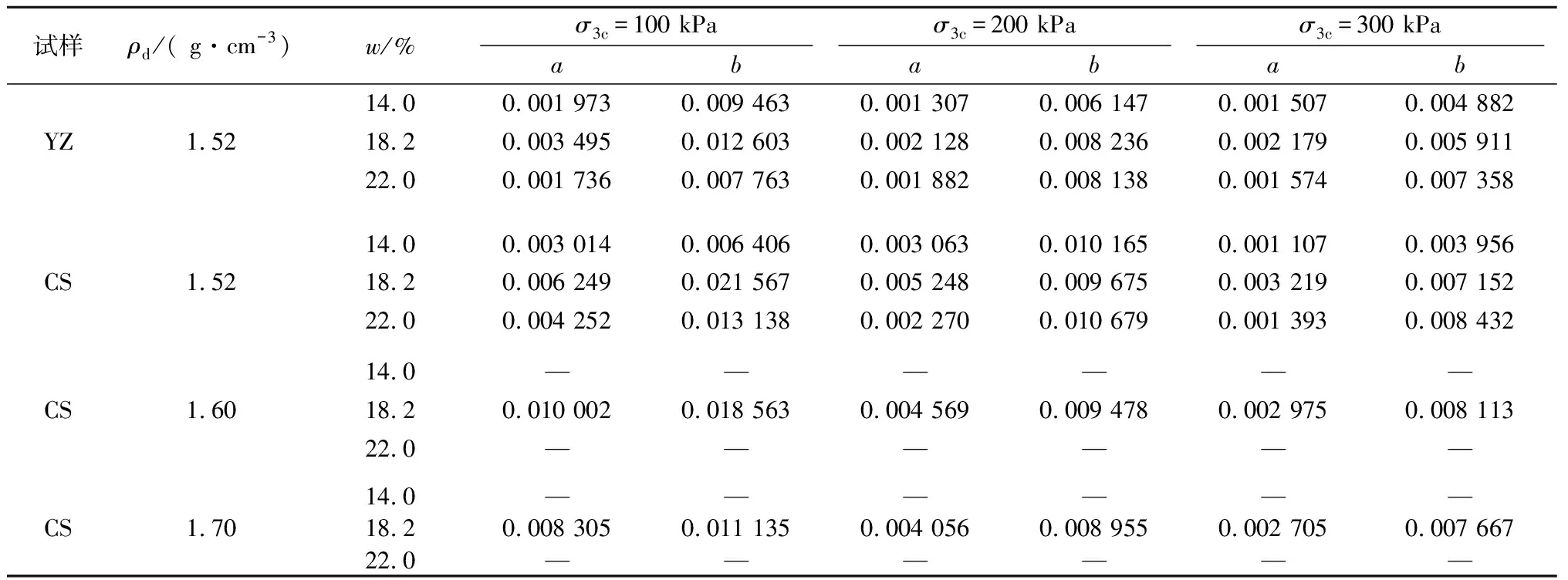
表2 双曲模型参数Table 2 Model parameters of established hyperbola model
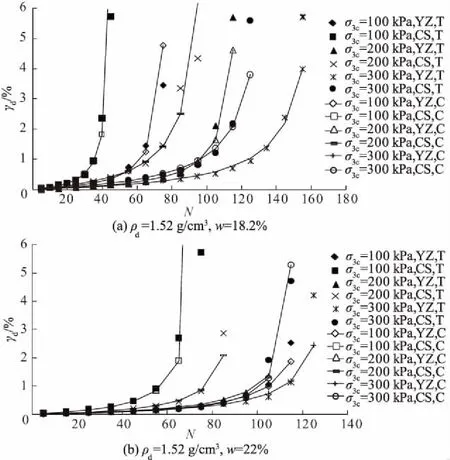
图7 黄土在动荷载作用下的动剪应变累积模型分析Fig.7 Model analysis of γd-N of loess under dynamic loads
Hardin-Drnevich模型以其参数少、形式简单的优点被广泛用于描述动剪切模量和动剪应变的关系[18],其表达式为
(7)
将式(6)代入式(7)可以得出式(8)。
(8)
利用式(8)可以预测随着动荷载的施加土体动剪切模量的发展趋势,从而可以描述土体随着动荷载的施加其剪切刚度的衰减过程[18]。
目前较为常用的循环荷载作用下土体的塑性应变累积模型为Monismith[19]提出的指数型模型,即
εp=ANb。
(9)
式中:εp为循环荷载作用下的塑性应变;A和b均为拟合参数。臧濛等[20]在前人研究的基础上,提出了可以描述循环塑形累积应变的改进模型,即
(10)
式中:ε为累积应变;a,b,c,m,δ为与应力条件和土性有关的参数。
臧濛等[20]提出的模型既可以描述较小循环荷载作用下的“稳定型”曲线,又可以描述较大循环荷载作用下的“破坏型”曲线。然而,式(9)和式(10)所示的模型均是适用于单级等幅循环加载方式,而本文研究采用的是逐级增幅循环加载方式,和之前研究采用的加载方式有明显不同。由于本文研究中循环荷载幅值逐级递增,所以应变累计曲线必然为“破坏型”曲线。另外,上述模型中的参数大部分只能通过拟合确定,尤其当拟合参数较多,给模型的使用带来了较多的不便。而本文提出的双曲模型,可以通过对模型公式进行转换而间接确定模型参数。式(6)为本文提出的双曲模型,通过变换,可以得出动荷载循环周次的倒数(1/N)和动剪应变的倒数(1/γd)呈线性关系,如式(11)所示,模型参数a,b则分别为直线的斜率和截距。通过模型公式的转换直接得出模型参数,使得本文提出的模型更便于使用。
(11)
4 结 论
(1)黄土的剪切刚度随着干密度和固结压力的增大、含水率的降低,有不同程度的提高;随着干密度和固结压力的减小、含水率的增大,黄土的动剪切应变累积速度加快,临界循环周次Nc明显增大,黄土在动荷载作用下经历更长的振动压密和振动剪切阶段。
(2)在逐级增大的动荷载作用下,黄土的动剪应变波动累积,但总体呈现压缩破坏趋势。在忽略试样径向变形的前提下,计算出了试样在动荷载作用下的孔隙比并得到了黄土的动力压缩曲线。
(3)在动荷载作用下,黄土的压缩特性明显区别于静力压缩。结构性在动力压缩过程中并未表现出来,原状和重塑黄土均存在临界动应力σdc。当σd<σdc时,黄土的动变形发展缓慢;而当σd>σdc时,黄土的动变形迅速积累,并很快达到破坏应变。
(4)提出双曲模型对黄土的动剪应变和循环周次关系进行描述,并利用差分进化法求得模型参数。在应变较大时,模型预测会产生一定的偏差,但是在小应变下(<3%),其能够较好地描述黄土的动剪应变累积特性。
