薄壁管滚珠旋压工艺参数多元函数拟合★
2018-09-18王巨堂王正谊
王巨堂, 王正谊, 熊 杰
(1.平朔工业集团有限责任公司, 山西 朔州 038500; 2.太原科技大学机械工程学院,
山西 太原 030024)
引言
滚珠旋压是旋压技术中的一种特殊的强力旋压技术,该工艺中的变形工具为滚珠,通过滚珠实现管类零件的成形加工。滚珠旋压是逐点变形,其变形区域小、变形应力大,并且旋压过程中的滚珠同时发生着公转和自转,可以实现运动的自调整,因此,该工艺所加工出的管件具有很好的加工精度和表面质量,并对硬度高且塑性指标差的金属材料的加工表现出很好的优越性。
1 滚珠旋压工艺
滚珠旋压工艺过程如图1所示,其中支撑环、圆锥模环和滚珠一起组成滚珠旋压模具,工件套在芯轴上,旋压模具在电机的驱动下发生旋转运动,使之与工件产生周向的相对运动;同时,随着芯轴的轴向进给,工件与旋压模具发生着沿工件轴向方向的相对运动,这样就实现了滚珠对工件的挤压变形,从而使得管坯旋薄。
本文中,R表示滚珠直径,Δt为旋压道次减薄量,f为进给比,α为旋压角。
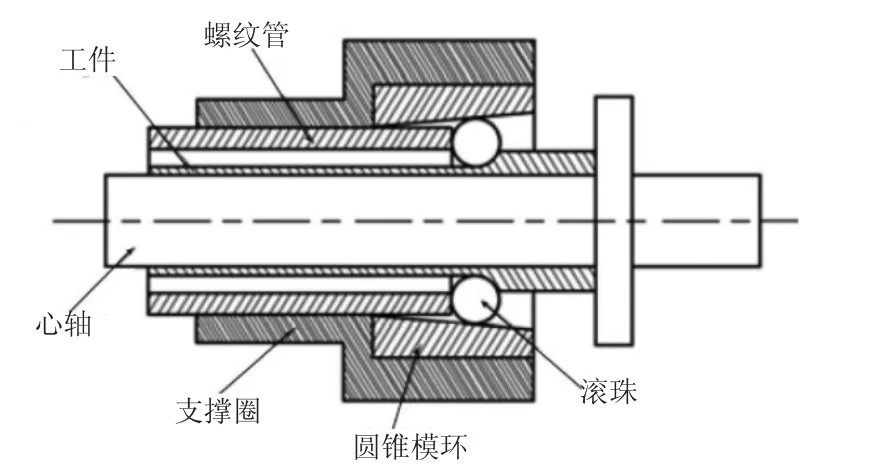
图1 滚珠旋压示意图
目前针对高速滚珠旋压工艺的研究,M.I.Rotarescu[1]通过理论推导和数值模拟的方法,推导出了旋压过程中滚珠的三向旋压力,在旋压力的理论计算上做出了突出的贡献和重要的奠基。T.Sumitomo[2]采用上限元法对管材内翅片的旋压力计算方法进行了研究。Li Maosheng[3]利用平面应变状态假设,得出了滚珠旋压力的计算公式。C.Sakaisha[4]通过对滚珠旋压工艺的应用,设计出了一种生产管材内螺纹的装置。Li Yong[5]对充液旋压加工铜管内壁沟槽和微细热管旋压拉拔复合成形机理进行了深入的研究。江树勇[6-7]利用有限元软件,详细地模拟并分析了带内筋管件的滚珠旋压,并对滚珠直径与旋压工艺之间的影响关系进行了详细的研究。
通过以上研究现状可知,当前在滚珠旋压工艺参数方面的研究上,主要采用的是经验选取的方式,即通过对旋压后管件的成形质量来反向确定旋压工艺参数的最佳值,而并非是从决定工件的塑性性能的根本原因出发来进行工艺参数的确定。已有的研究表明,减少材料的应力三轴度可以提高材料的塑性。应力三轴度σ*按照下式给出:
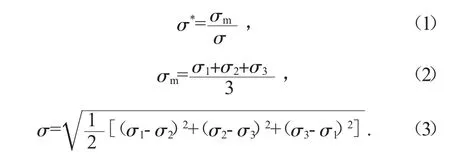
式中:σm为球应力,σ1、σ2、σ3依次为最大主应力、中间主应力、最小主应力,σ为von Mises等效应力。通常来讲,三轴度Rd越小,材料的塑性变形极限就会越高,具有越好的塑性成形能力。
2 平均应力三轴度有限元仿真
本文采用商业有限元软件ABAQUS来进行旋压过程的模拟,计算中对模型进行相应简化,忽略掉旋压模具,直接定义滚珠的运动;同时,考虑到计算效率与计算结果的精确度,设置滚珠、推力环、芯棒为三维解析刚体,设置管坯为弹塑性可变形体;采用八节点线性六面体单元C3D8R,并对塑性变形区域进行网格细化。以AZ31镁合金薄壁管作为管坯,其材料属性见表1。
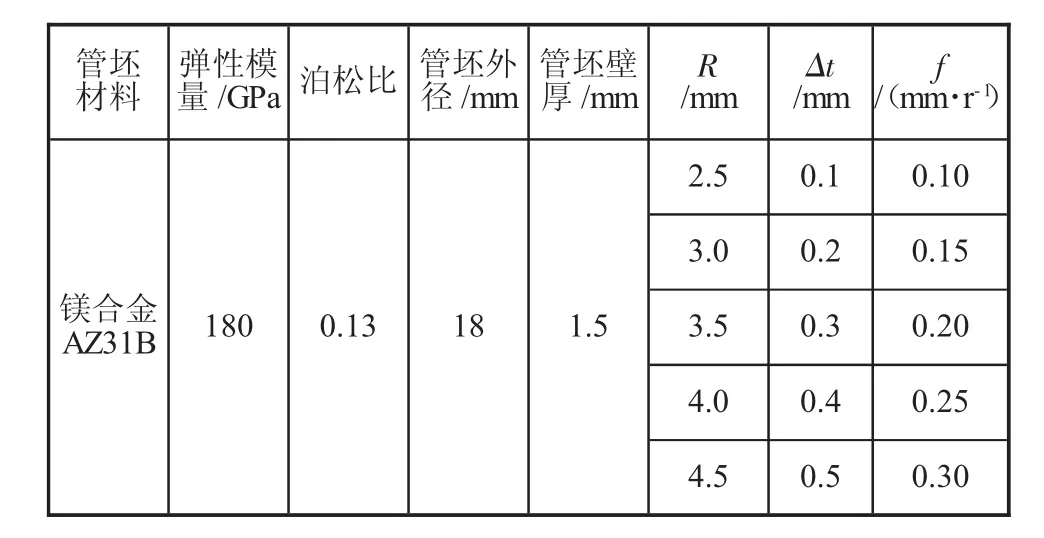
表1 管坯材料属性及工艺参数
滚珠旋压过程中,滚珠与管坯之间发生的接触挤压变形区域除了滚珠正下方的金属区域外,其附近受到影响的变形区域也包括其中。故本文把滚珠与管坯直接接触区域和其附近的区域来看做单个滚珠的变形影响区,如图2所示,并将此变形影响区的应力三轴度平均值(AVST)作为考察对象。
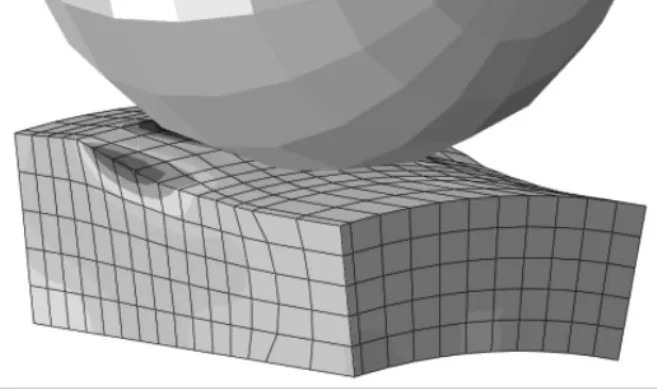
图2 单个滚珠变形影响区
把单个滚珠的变形影响区内的所有单元设为一个集合进行输出,提取出集合内所有单元的相对应力三轴度值,并把提取的应力三轴度值进行求取平均值,将所求得的平均值看做变形影响区的平均应力三轴度,计算结果见表2。
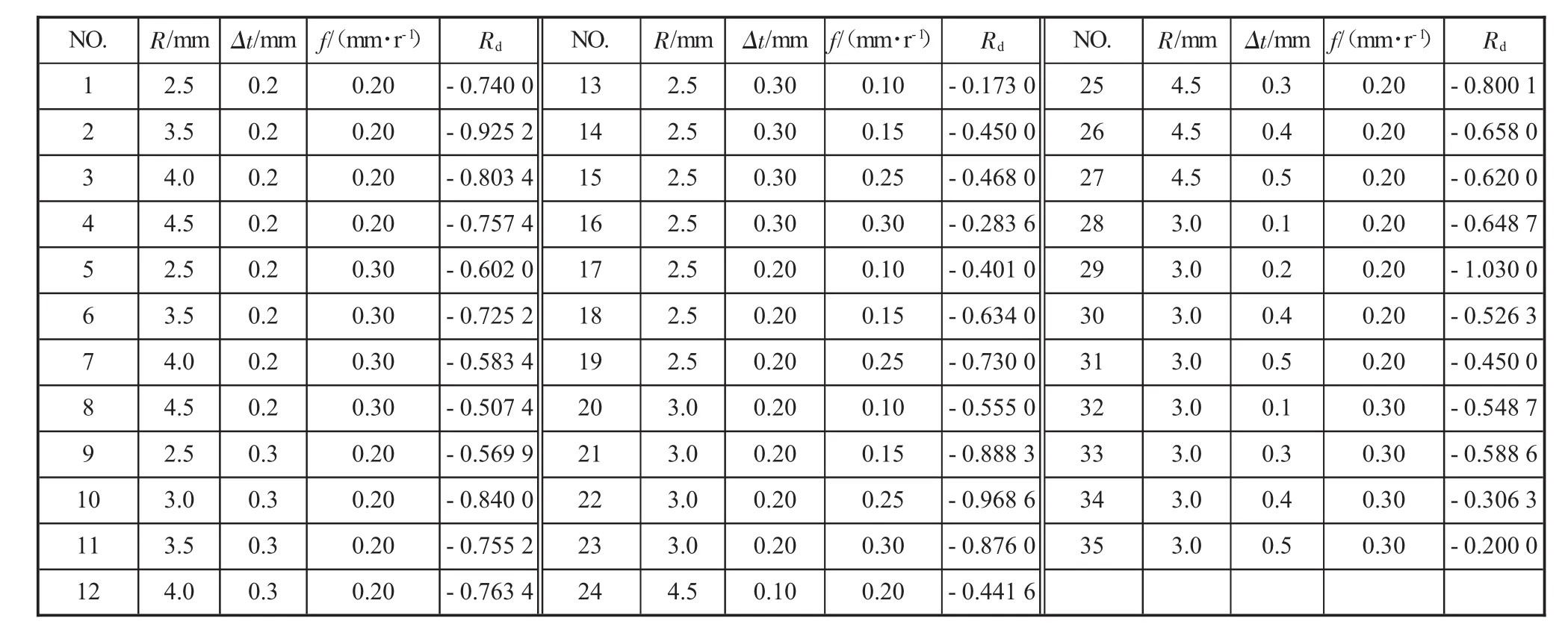
表2 各工艺参数下平均应力三轴度值
3 多元非线性函数关系拟合
通过上述的分析结果,得到了单个滚珠变形影响区的AVST随滚珠旋压工艺参数变化的影响趋势,并由表2所计算出的结果数据,对滚珠直径、减薄量和进给比与平均应力三轴度之间的关系进行非线性函数拟合,得到AVST随工艺参数变化的函数关系式。这样在某个工艺参数发生改变时,能够方便地匹配其余工艺参数。
根据仿真结果的数据趋势,选择三元三次多项式作为拟合函数模型。当采用标准形式的三元三次多项式模型进行数据拟合时,多项式中RΔtf、RΔt、Rf、与Δtf之间的共线性关系十分明显,这就导致将这四项同时进入拟合函数模型时,模型就会出现失真的情况,使得拟合结果无效。所以,在标准三元三次多项式模型的基础上去掉这四项后,得到的最终拟合函数模型如下:
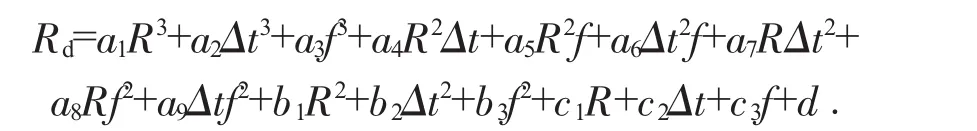
代入表2中数据,得到拟合结果如表3、表4。

表3 拟合函数参数
考虑到拟合函数拟合度的好坏,采用如表4的判定参数进行拟合度判定。
为了使拟合函数与实际测定值之间的契合度进行更加直观地表述出来,将实测点数据代入拟合函数中计算求得理论值,并将有限元计算值与拟合函数的计算值绘制在下图3中。

表4 拟合度判定参数
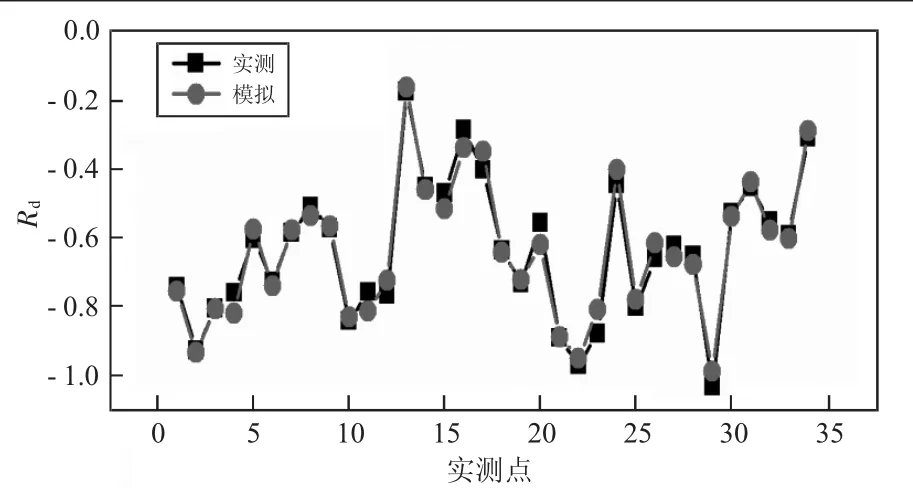
图3 AVST实测值与拟合函数计算值对比图
从图3中可以看到,AVST的有限元计算值与拟合函数的计算值很接近,没有出现偏离度较大的数据点,具有较高的重合度,说明本文给出的拟合函数模型是可靠可行的。
4 结论
1)以AZ31镁合金薄壁管为对象,通过有限元计算得到了对不同工艺参数下滚珠旋压变形影响区的平均应力三轴度值;
2)选择三元三次多项式作为拟合函数,得出了精确的拟合函数各项参数;
3)通过多元函数的拟合,将有助于确定最小应力三轴度对应的工艺参数值,使薄壁管滚珠旋压的塑性成形性能提升,有助于改善难变形金属如镁合金的滚珠旋压塑性变形性能。
