空间四连杆引纬机构刚柔耦合动力学分析与仿真
2018-09-18金国光李文启畅博彦
金国光 ,李文启 ,魏 展 ,畅博彦
(1.天津工业大学机械工程学院,天津 300387;2.天津工业大学天津市现代机电装备技术重点实验室,天津300387)
引纬机构是剑杆织机的核心机构[1],其作用是通过剑杆夹持纬纱引入梭口,使经纱与纬纱实现交织形成织物.空间四连杆引纬机构具有转速高、运动平稳、空间体积小、制造成本低等优点,被广泛应用于剑杆织机上.该机构由球面4R机构带动平面四连杆机构经齿轮放大机构实现剑杆的往复直线运动,进而实现引纬动作[2].为了提高剑杆织机转速,增加剑杆织机工作效率,许多研究学者对该机构进行了运动学和动力学方面的研究.何勇等[3]分析出空间RSSR机构向球面4R机构转化的必要条件,根据所推出的条件设计出一种满足空间四连杆引纬机构需要的球面4R机构,为空间四连杆引纬机构的设计提供了参考.张雷等[4]基于非连续接触模型和等效杆长理论,建立了含间隙和尺寸误差的空间四连杆引纬机构运动学模型,并对引纬机构进行了运动精度分析.周香琴等[5]利用Pro/E软件对空间四连杆机构进行了刚体动力学分析,得出了主轴所受载荷的变化规律.余克龙等[6]研究了柔性条件下,不同材料的传动曲柄对空间四连杆引纬机构动力学性能的影响.
随着剑杆织机高速化的发展趋势,空间四连杆引纬机构在高速运行过程中,将不可避免的产生柔性变形,因此仅将该机构中各构件看成刚性体已不能准确有效地反映其动力学性能.本文应用基于ANSYS与ADAMS联合仿真[7-9]的方法,对该机构进行刚柔耦合动力学建模与仿真.将空间四连杆引纬机构中核心部件十字摇轴进行柔性化,建立空间四连杆引纬机构的刚柔耦合模型;分析剑带的运动规律,研究高速运行状态下引纬机构中十字摇轴的柔性变形对引纬运动的影响;将ADAMS仿真生成的载荷文件输入到ANSYS中,对十字摇轴进行瞬态动力学分析[10-12],为引纬机构的优化设计提供理论参考.
1 空间四连杆引纬机构工作原理
剑杆织机空间四连杆引纬机构如图1所示.
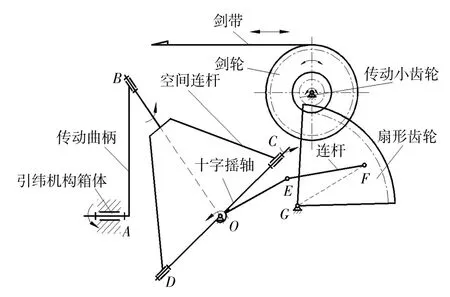
图1 空间四连杆引纬机构简图Fig.1 Diagram of spatial four-bar linkage weft insertion mechanism
由图1可知,该引纬机构由三大部分组成:①由引纬机构箱体、传动曲柄、空间连杆、十字摇轴组成的球面4R机构;②由十字摇轴、连杆、扇形齿轮组成的平面四连杆机构;③由扇形齿轮、传动小齿轮、剑轮、剑带组成的齿轮放大机构.
空间四连杆引纬机构传动路线为:传动曲柄绕A轴旋转,带动空间连杆作空间定点转动.十字摇轴在引纬机构箱体的约束和空间连杆的带动下作往复摆动.十字摇轴上OE杆作往复摆动,通过连杆带动扇形齿轮往复摆动.扇形齿轮的往复摆动,经过传动小齿轮、剑轮放大之后,传递到剑带上,使剑带作往复直线运动,以实现空间四连杆引纬机构的引纬动作.
2 基于拉格朗日方程的柔性体运动微分方程
首先,应用有限元法对柔性体进行离散化处理.规定柔性体中各单元节点的广义坐标用表示,则柔性体单元中任意一点处的位移可用广义坐标与型函数表示为
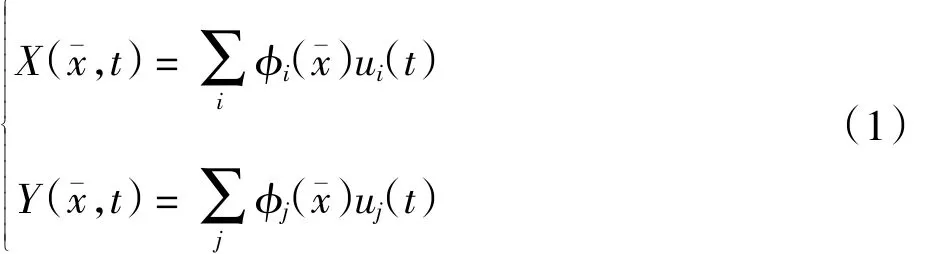
其次,基于拉格朗日方程建立柔性体单元的运动微分方程.忽略截面转动的动能,动能表达式为
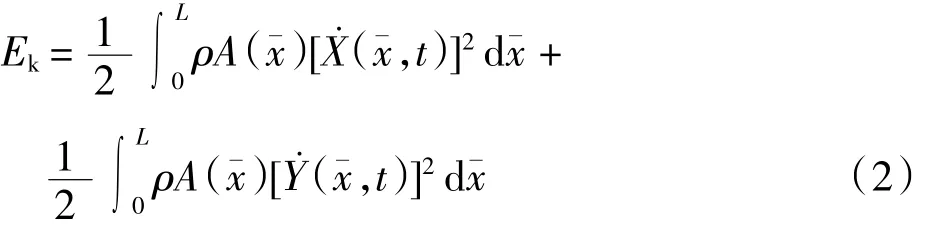
对柔性体单元的变形能进行推导,假设只计入柔性体单元在弯矩作用下的弯曲变形和在轴向力作用下的拉伸、压缩变形,则根据材料力学知识,变形能可表示为
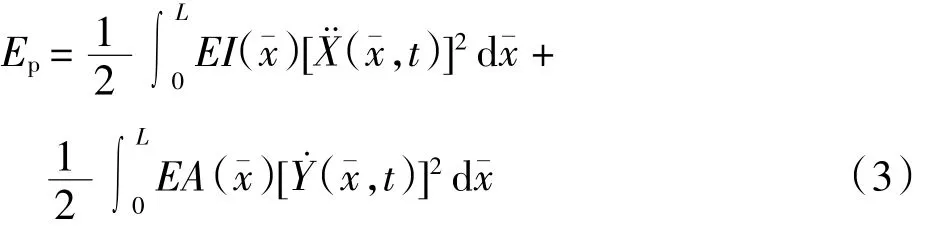
根据式(1)-(3)可得到基于拉格朗日方程的柔性体运动微分方程
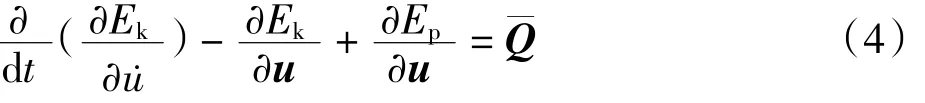
式中:u为单元广义坐标列阵;Q 为单元广义力列阵.
3 空间四连杆引纬机构刚柔耦合动力学仿真
3.1 建立空间四连杆引纬机构刚体模型
对国产某型剑杆织机空间四连杆引纬机构进行测绘,根据测绘所得数据在SolidWorks中建立引纬机构三维实体模型.将该模型另存为Parasolid格式文件.打开ADAMS中File Import对话框,将空间四连杆引纬机构三维实体模型导入到ADAMS中,生成空间四连杆引纬机构刚体模型.为该模型中各构件按照运动副的约束关系添加连接副,并且在ADAMS环境中给各构件添加材料,各构件材料及其密度如表1所示.

表1 各构件材料密度Tab.1 Material density of each component
3.2 建立空间四连杆引纬机构刚柔耦合模型
空间四连杆引纬机构中的十字摇轴在该机构中起着重要的作用,它连接了球面4R机构和平面四连杆机构,是引纬机构中传递运动和力的重要构件.现对十字摇轴进行柔性化处理:①将SolidWorks中建立的十字摇轴三维实体模型另存为Parasolid格式文件;②将生成的文件导入ANSYS中,对十字摇轴采用自由网格划分技术,划分单元选用SOLID185和MASS21,弹性模量设置为206 GPa,泊松比设置为0.26,密度设置为7900 kg/m3,在十字摇轴的连接处设置刚性节点,并建立刚性区域(如图2所示),然后输出MNF中性文件;③打开ADAMS中建立的空间四连杆引纬机构刚体模型,应用Rigid to Flex命令将ANSYS生成的十字摇轴中性文件替换原来的刚性十字摇轴,并在十字摇轴的连接处重新定义连接副,其他各构件间的连接副保持不变.生成空间四连杆引纬机构的刚柔耦合模型,如图3所示.
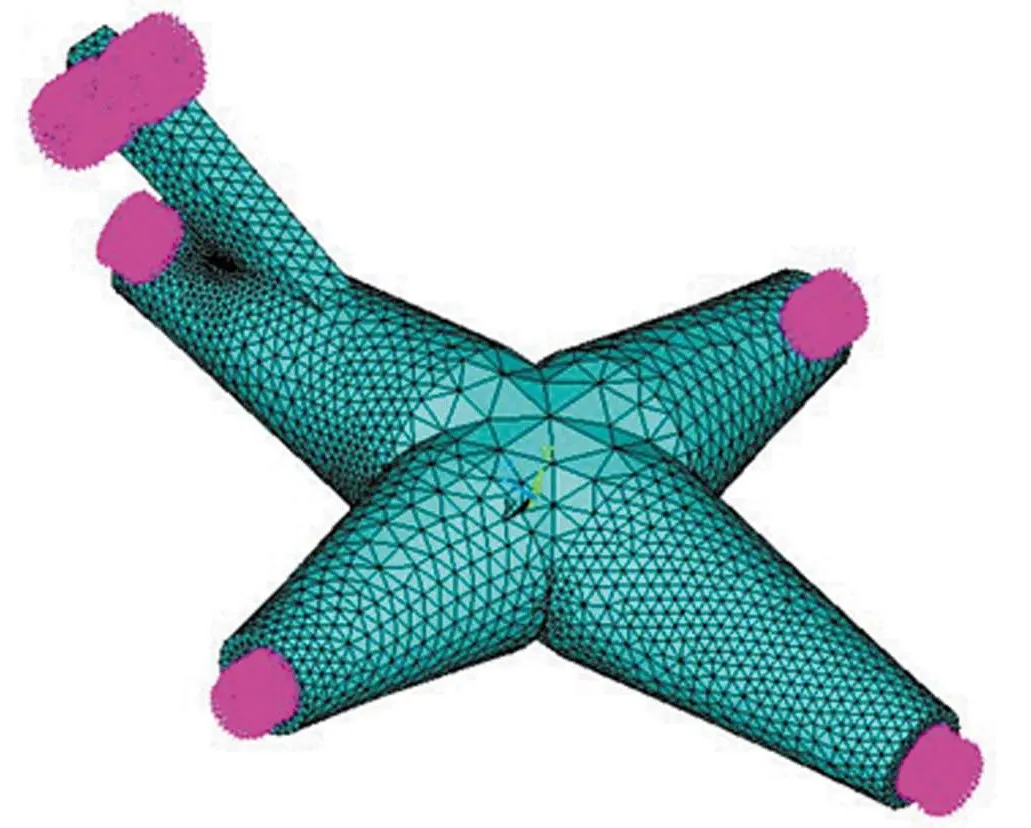
图2 十字摇轴刚性区域Fig.2 Rigid region of cross axis
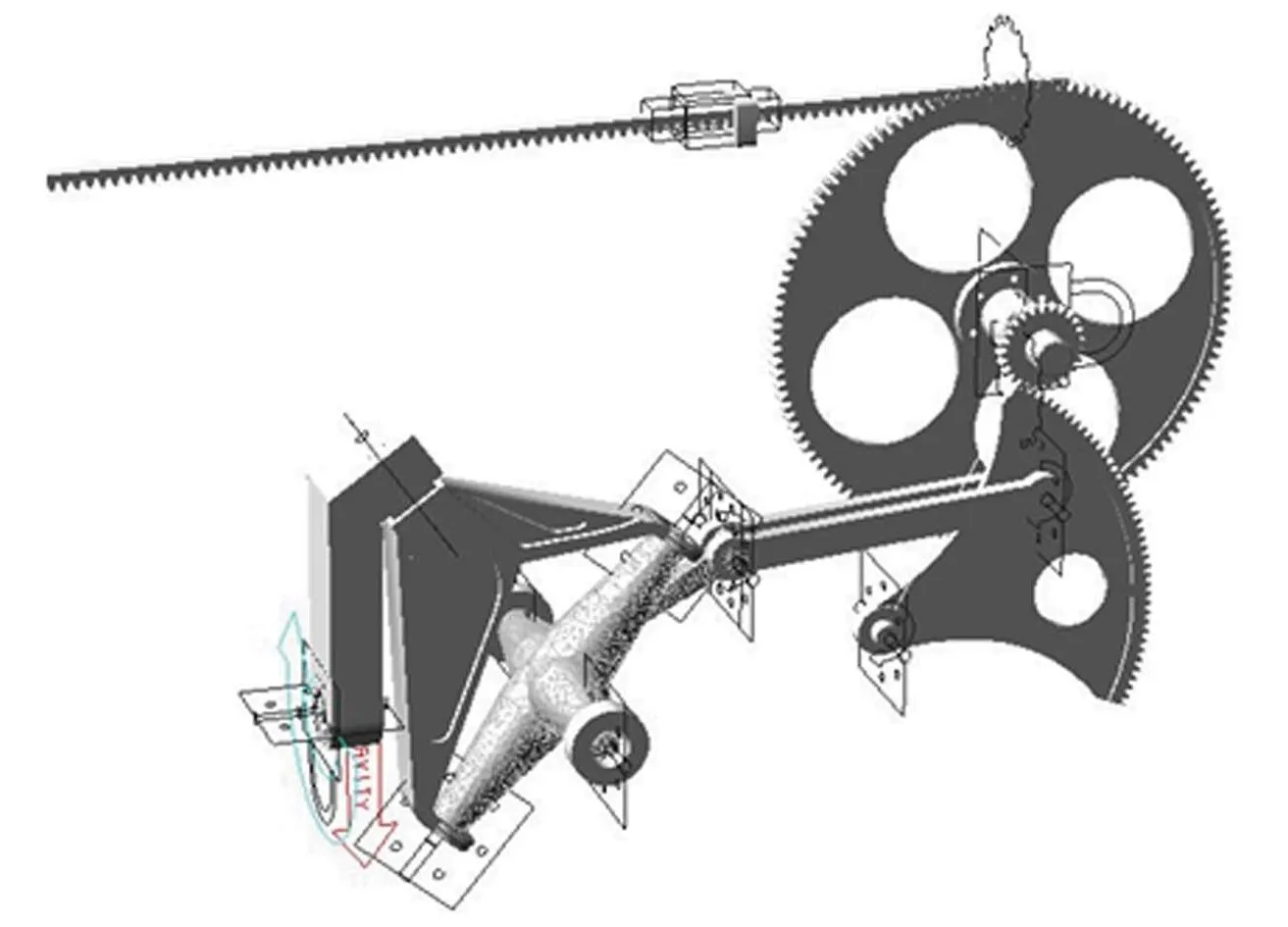
图3 空间四连杆引纬机构刚柔耦合模型Fig.3 Rigid-flexible coupling model of spatial four-bar linkage weft insertion mechanism
3.3 动力学仿真与分析
在ADAMS中,首先对空间四连杆引纬机构进行刚体动力学仿真,设置织机主轴转速为400 r/min,得到一个周期内剑带的位移、速度和加速度曲线.然后对空间四连杆引纬机构进行刚柔耦合动力学仿真,同样设置织机主轴转速为400 r/min,得到一个周期内剑带的位移、速度和加速度曲线.将刚体动力学仿真结果与刚柔耦合动力学仿真结果进行对比,得到剑带的位移、速度、加速度对比曲线,分别如图4、图5和图6所示.
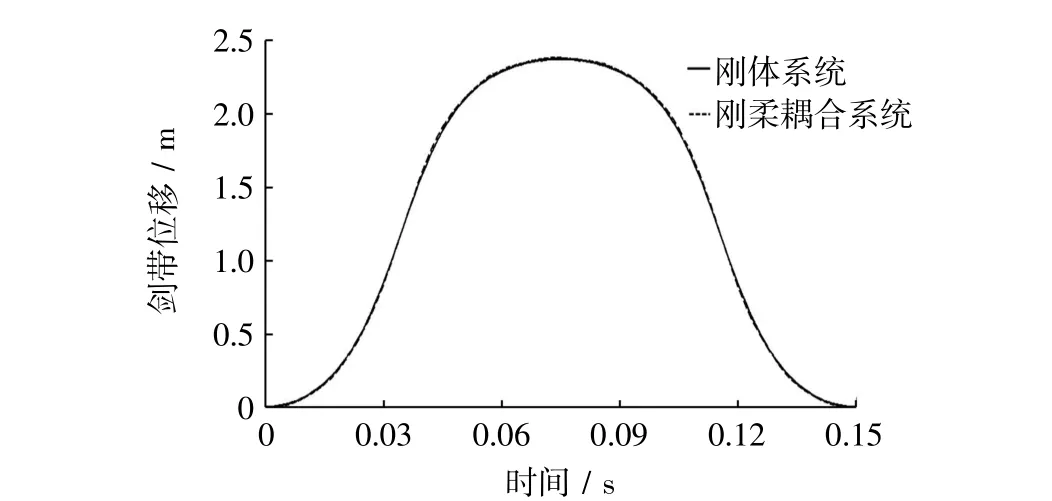
图4 剑带位移曲线Fig.4 Displacement curve of rapier transfer band
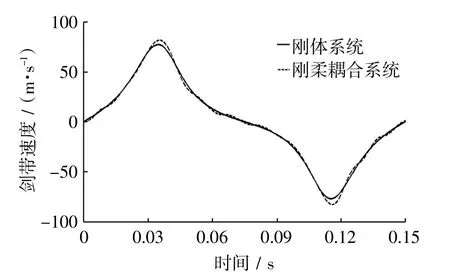
图5 剑带速度曲线Fig.5 Velocity curve of rapier transfer band
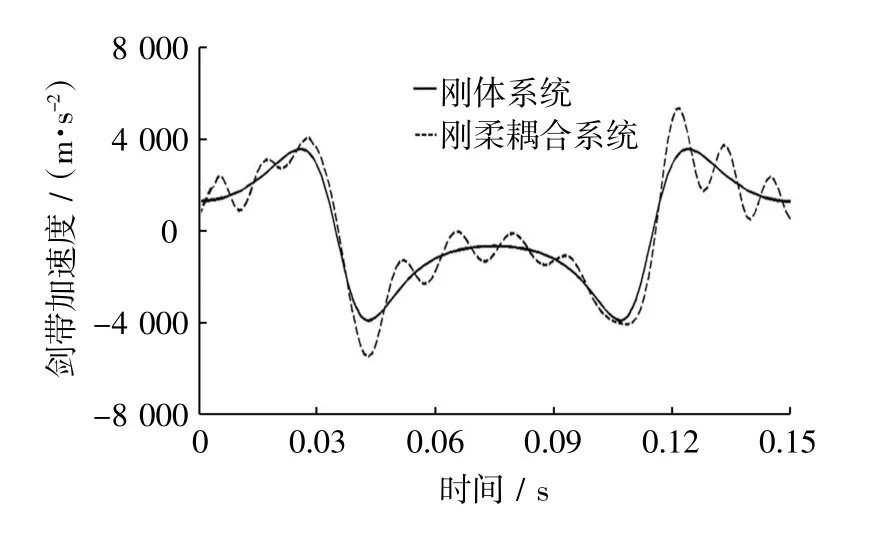
图6 剑带加速度曲线Fig.6 Acceleration curve of rapier transfer band
从图4、图5和图6可以看出:①十字摇轴的柔性化对剑带的位移曲线影响较小,刚体仿真与刚柔耦合仿真中剑带的最大位移分别为2.36 m和2.37 m,两者最大位移基本一致;②刚体仿真与刚柔耦合仿真相比,两者的剑带速度最大偏差为4.38 m/s,仅占了刚体仿真中剑带速度的5%,故也可认为十字摇轴的柔性化对剑带速度特性影响较小;③刚体仿真与刚柔耦合仿真相比剑带加速度曲线波动较大,在0.122 s处最大偏差达到了刚性仿真条件下的66%;而在时间为0.043~0.106 s,即纬纱交接阶段,剑带加速度平均偏差为3%.
分析引纬工艺特点,剑带加速度的大幅波动会对纱线产生较大冲击力,造成断纱率提高,进而降低剑杆织机的引纬稳定性.而纬纱交接阶段加速度波动则会降低纬纱交接的准确性.引纬稳定性和准确性都是影响剑杆织机工作效率的重要因素.
工业生产中,为了提高剑杆织机的工作效率,经常使剑杆织机处于高转速下运行,现就织机主轴在不同转速下十字摇轴的柔性化对剑带加速度特性的影响进行分析研究.
在ADAMS环境中,分别在织机主轴转速为400 r/min、500 r/min和600 r/min时对该型空间四连杆引纬机构进行刚体动力学仿真和刚柔耦合动力学仿真,得到剑带加速度对比曲线,如图7所示.
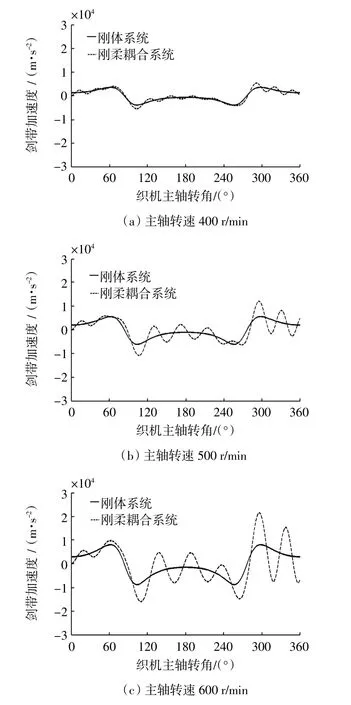
图7 剑带加速度曲线Fig.7 Acceleration curve of rapier transfer band
通过对图 7(a)、(b)、(c)的对比可以得出如下结论:随着剑杆织机主轴转速的提高,十字摇轴柔性化造成剑带加速度波动变大.根据引纬工艺的要求,织机主轴转角为105°~255°之间时,剑杆织机引纬机构将进行纬纱交接,此时需要较为平缓的运动规律.分析图 7(a)、(b)、(c)可以看出,纬纱交接阶段,织机主轴转速为400 r/min时,剑带加速度平均波动为3%;织机主轴转速为500 r/min时,剑带加速度平均波动为5%;织机主轴转速为600 r/min时,剑带加速度平均波动为6%.即随着织机转速的提高,纬纱交接阶段的剑带加速度波动增大,而剑带加速度波动增大会导致纬纱无法准确有效的进行交接,进而降低剑杆织机工作效率.因此,过度的增加剑杆织机主轴转速不一定能提高织机的工作效率,综合考虑上述因素,得出本文所研究的剑杆织机的最佳主轴转速为400 r/min.
3.4 基于ANSYS的柔性十字摇轴瞬态动力学分析
在ADAMS环境中,设置织机主轴转速为400 r/min,对引纬机构进行刚柔耦合动力学仿真.仿真结束后通过ADAMS中的EXPORT命令导出柔性化十字摇轴的载荷文件.然后,在ANSYS环境中打开柔性体十字摇轴,在SOLUTION求解器下选择分析类型为瞬态动力学分析Transient.最后,通过ADAMS与ANSYS的接口将ADAMS中生成的载荷文件输入到ANSYS中并对该模型进行求解.在十字摇轴的3个转动副处分别选取节点1、节点2、节点3,如图8所示.在ANSYS时间历程后处理器POST26中输出3个节点应变曲线,如图9所示.
图8 十字摇轴节点Fig.8 Node of cross axis
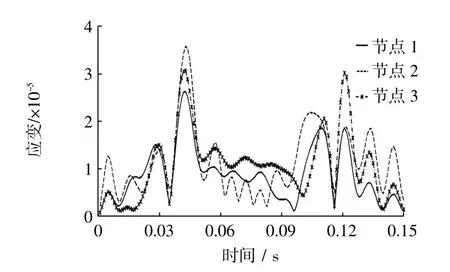
图9 节点应变曲线Fig.9 Strain curve of node
由图9可以看出,十字摇轴3个节点应变极值均在0.042 s与0.122 s处取得.从图6中刚柔耦合系统剑带加速度曲线可以看出,在0.042 s时剑带加速度取得反向最大值,在0.122 s时剑带加速度取得正向最大值.由于剑带加速度取得极值时,势必造成十字摇轴连接处应变取得极值,故上述结论验证了所建刚柔耦合动力学模型的正确性.
对十字摇轴进行应变分析,通过ANSYS普通后处理器POST1得到十字摇轴所受应力云图,如图10所示.通过应力云图即可得出十字摇轴所受应力最大值及其对应位置,为后续引纬机构的优化设计提供理论参考.
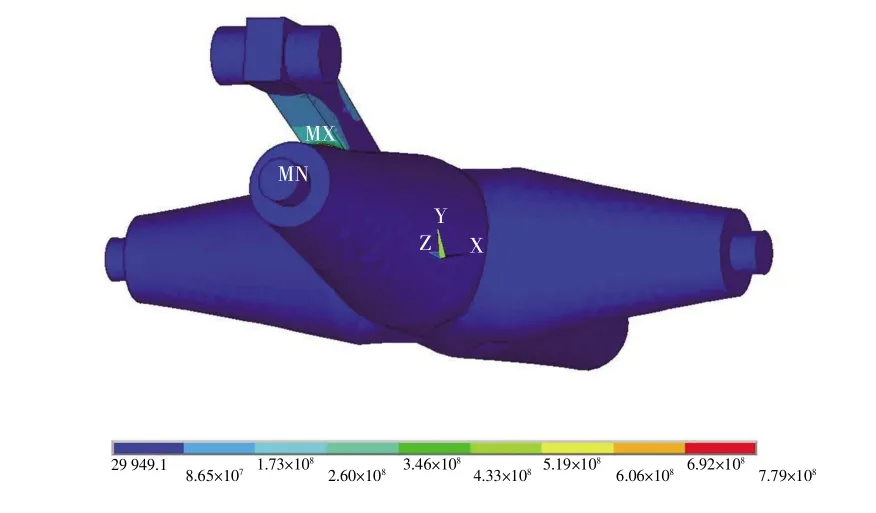
图10 十字摇轴应力云图Fig.10 Cross axis stress cloud map
4 结论
(1)基于ANSYS与ADAMS建立了空间四连杆引纬机构刚柔耦合模型,并对其进行了刚柔耦合动力学仿真.刚柔耦合动力学仿真可以更加准确、有效地反映空间四连杆引纬机构在高速运行时的动力学性能.
(2)通过刚体动力学仿真结果与刚柔耦合动力学仿真结果对比发现十字摇轴的柔性变形会影响引纬动作的准确性与稳定性.并且织机主轴转速越高,剑带加速度波动越明显,越不利于引纬.本文所用剑杆织机的最佳转速为400 r/min.
(3)利用ANSYS对柔性十字摇轴进行瞬态动力学分析,找到十字摇轴所受应力最大点,并得到十字摇轴连接点处的应变曲线,为空间四连杆引纬机构的优化设计提供理论参考.
